面向复杂网络的多属性决策关键节点识别算法研究*
宁 阳 武志峰 张 策
(天津职业技术师范大学信息技术工程学院 天津 300222)
1 引言
网络中的关键点识别算法是网络科学的重要研究内容之一。关键点识别算法的研究在医学、社会学、网络安全、电力交通、政治与经济学领域具有重要意义。在社会网络中通过最有影响力的人的查找,可以控制流言的传播;在疾病爆发区域通过易感人群的查找,可以对疾病进行有效地预防和控制;在城市交通系统、电力系统中通过对关键枢纽的识别和重点维护,可以降低经济损失风险。对复杂网络有效管理的关键是有效识别网络中的关键结点。目前,解决这一问题的算法通常采用基于图论的概念和术语,将具体实际问题抽象为图,进而得到具体实际网络的拓扑性质。相关研究通常是在常用指标进行改进和将多个指标进行融合[1~4],因为度中心性[5]算法虽然简单高效,却没有考虑网络的全局结构;介数中心性[6]、接近中心性[7~8]考虑了网络的全局结构,但算法时间复杂度高,并不适合在大规模网络中应用;Kitsak等考虑节点在网络中的位置,提出k-shell[9]分解方法,能够适用于大规模网络,由于网络中存在大量度值相同的节点,k-shell排序方法的分辨率不高;为解决k-shell方法划分结果粗粒化的问题,邓凯旋[10]等提出根据节点删除过程中迭代层数,结合节点度和邻居节点,改进k-shell方法识别关键节点;李懂[11]等提出融合节点度和K核迭代次数的多属性决策方法,通过熵权法衡量节点重要性;Liu[12]等提出结合当前节点所在ks值及最大ks值,计算节点到最大K核节点集合的最短距离,进而区分ks值相同的节点;Bae等[13]提出考虑局部范围内节点的ks值,节点两层邻居节点的ks值和,借鉴局部中心性思想改进k-shell;顾亦然等[14]将k-shell与重要度贡献矩阵相结合,引入影响度的概念进行关键节点识别。然而,随着网络规模的不断增大,现有算法在衡量节点影响力的准确性和效率上,均出现了明显不足,难以应对日益复杂网络的各类新问题。本文基于节点度、改进的K核迭代次数指标,使用熵权法[15]、灰色关联度分析法[16]多属性决策关键节点,更有效地进行关键节点识别。
2 相关概念
2.1 网络表示
将一个具体网络抽象为一个由点集V和边集E组成的图G=(V,E)。顶点数记为N=|V|,边数记为M=|E|。无向无权图G的邻接矩阵A=(aij)N×N是一个N阶方阵,第i行第j列上的元素aij定义如下:

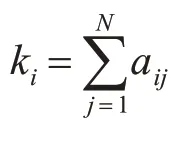
2.2 相关算法
k-壳分解,通过去除网络中度值为1的节点及其连边,将过程中产生新的度为1的节点划分到同一层,直至网络中每个节点的度值至少为2。重复操作,去除网络中度值为2的节点及其连边,直至网络中不再有度值为2的节点为止。k=1,2,3…,直至网络中的每一个节点均被划分到相应的k-壳中,每一个节点对应唯一的ks值,且k-壳中所包含的节点度值满足ki≥ks。所有ks≥k的k-壳的并集为网络的k-核[17]。实际网络中就某些问题而言度大的节点通过k-壳分解的方法,由于具有较小的ks值不一定是重要节点[18]。图1是由17个顶点组成的小网络,节点v6的度大于节点v11,ks值小于v11。
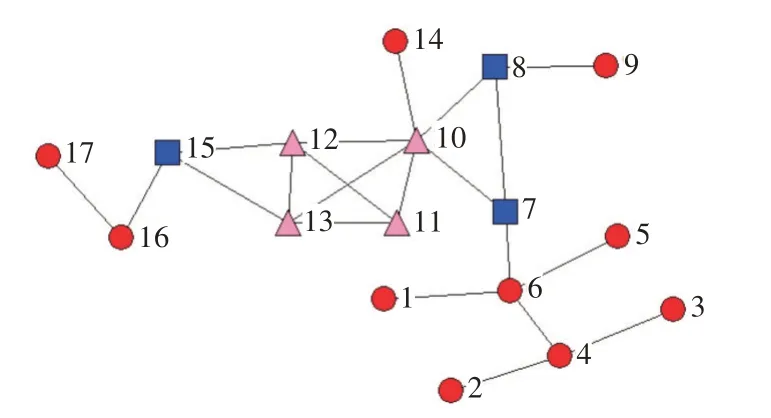
图1 示例图三角形节点ks=1方形节点ks=2圆形节点ks=3
其中公式涉及的k(i)为节点度,n(i)为节点迭代次数,Γ(i)为节点i的邻居节点集合。
文献[10]通过k-shell分解过程中节点被删除的顺序定义迭代次数增加ks值区分程度,结合节点度衡量节点重要性,该指标值越大,节点越重要,如式(1)所示:
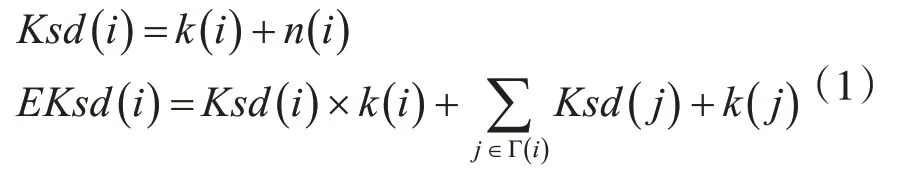
文献[11]通过熵权法计算节点度值和迭代次数两个指标的权重w1、w2,计算权重因子Vw,结合节点本身及邻居节点的权重因子得到节点的综合重要性值DK(i),如式(2)所示:

文献[13]提出通过邻居节点的ks值衡量节点重要性,通过扩展得到Cnc+值,如式(3)所示:

3 k-shell多属性决策改进算法
3.1 改进K核迭代次数指标
节点度是一种局部性指标,可以反映节点的影响能力,K核迭代次数反映节点的全局位置,计算K核迭代次数时,k-壳分解方法中的节点删除顺序不再从度值小于k,k=1,2,3…累计计算,直到网络中每个节点都对应唯一一个ks值。改为按照度值删除度值最小的节点,ks值递增,计算每个节点的ks值;K核迭代次数是在ks值的基础上计算得到,剥除网络中度值小于等于k的节点,若产生新的满足剥除条件的节点,此时依旧首先去除度值最小的节点,ks值不变,节点删除的迭代次数累加,节点的迭代次数即被删除的顺序。通过计算节点到最大核节点集的平均距离改进K核迭代次数,进一步区分相同K核迭代次数值,以此划分节点重要程度,本质为了增加ks值区分程度,解决粗粒化划分问题。节点度和K核迭代次数为效益型指标[15]。
定义成本型指标节点到最大核节点的平均距离Ave_d和改进后迭代次数值n′,如式(4)所示:

其中,φ(G)为网络中最大核节点集合。
3.2 构造规范化决策矩阵
通过计算节点的上述指标,构建规范化决策矩阵RM×N,M=2,N为网络中节点个数。Rij分别表示度值、改进迭代次数标准化后值,i=1,2。
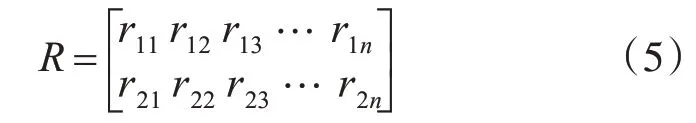
规范化决策矩阵处理方式[15]:

3.3 熵权法确定权重
熵权法根据各项指标所包含的信息量的大小来确定指标权重的客观赋权法[15,19]。首先对决策矩阵R进行归一化处理,得到R′,其次计算第i项指标的熵值Evi,如式(8)所示,然后根据熵值Evi计算两个指标各自权重wi:
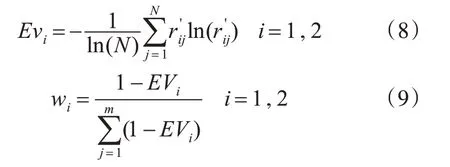
3.4 灰色关联度分析法确定权重
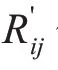
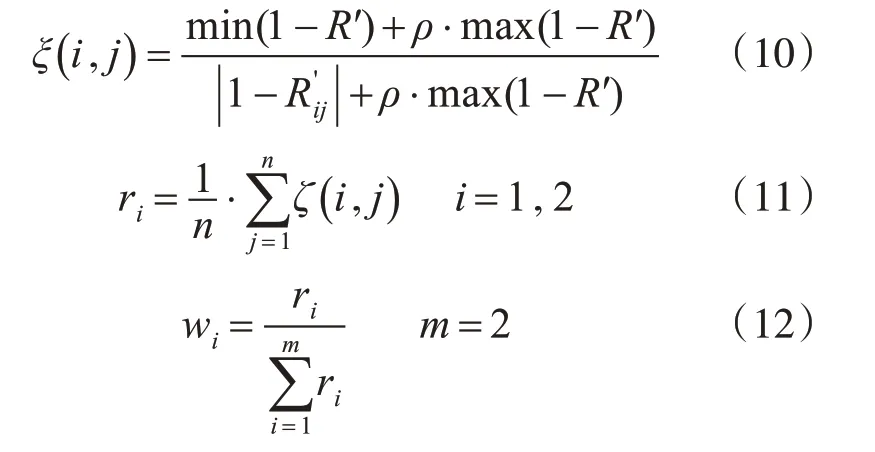
3.5 综合评估节点重要性
根据wi综合评估节点重要性:

考虑局部信息,结合邻居节点定义重要性评价指标:
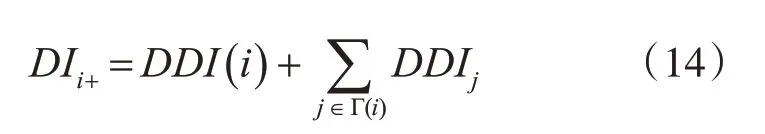
其中,使用熵权法确定权值计算得到的衡量节点重要性指标记为EDI,使用灰色关联度分析法确定权重方法得到的指标记为GDI。
算法步骤:
1)计算网络中每个节点的度、改进的迭代次数;
2)分别使用熵权法、灰色关联度分析法按照式(6)、(7)效益型指标规范化决策矩阵;
3)按照两种赋权方法计算每个指标的贡献权重;
4)根据式(14)计算每个节点的EDI、GDI值。
4 实验分析
4.1 评价标准
4.1.1 单调性指标
本文算法为了解决k-shell方法划分结果粗粒化问题,使网络中的节点尽可能分配单一排序等级,排序相同值的节点少,单调性指标值越大。采用文献[11]中方法评价不同排序方法的单调性。Monotonicity定义如下:
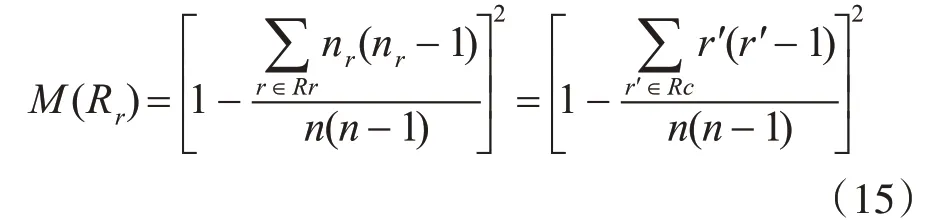
其中Rr为排序等级列表,n为排序结果中元素数目,nr为相同等级节点数目。为简化计算,Rc为划分到相同等级中节点个数非1的列表,该指标公式用于衡量排序结果中相同值所占列表比例。
4.1.2 相关性指标
本文使用SIR传播模型获得标准排序结果,N个节点的状态可分为三类。
1)S:易染状态,初始条件下所有节点均为易染状态,该节点以β的概率被邻居节点感染;
2)I:感染状态,感染某种病毒作为传染源的节点,该个体以β概率感染其邻居节点;
3)R:移除状态,也成免疫状态或恢复状态,感染状态节点以β概率感染邻居易感节点后,以γ概率变为R移除状态,不再具有感染能力和易感特性;
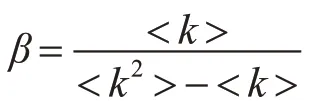
使用Kendall相关系数τ计算两个排序序列list1和list2之间的相似性,定义如下:
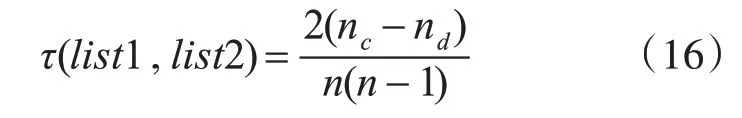
其中,nc表示两个序列中同序对的个数,nd表示两个序列中异序对的个数,n表示排序序列列表的长度。τ值越大,两个列表之间相似性越大。
例:list1={1,2,3,4},list2={1,3,2,4}。

表1 list1与list2二元组集合
4.2 仿真实验
根据上述分析,为了验证本文提出方法的有效性及准确性,设计两组对比实验,在六个网络数据集进行仿真实验,并与Ks、Cnc+、EKsd、DK算法指标进行对比分析,比较算法排序结果单调性;使用SIR传播模型计算标准排序结果,计算各中心性算法与SIR的Kendallτ相关系数;比较熵权法、灰色关联度分析法确定权重的计算方法的差异。具体网络拓扑结构统计特征如表2所示。
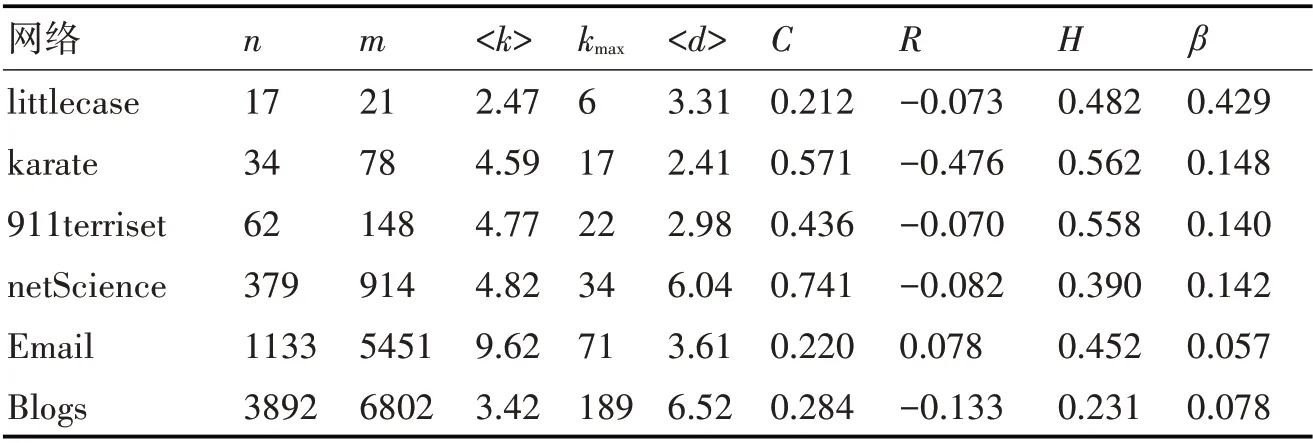
表2 网络拓扑结构统计特征
littlecase为一个案例网络,karaze[20]是具有社团结构的网络,由美国一所大学的空手道俱乐部成员组成的关系网;911terriset[21]网络是恐怖袭击网络,每个节点代表一名恐怖分子,节点之间的边代表恐怖分子之间的联系;netScience[22]是科学家合作网络,网络代表科学家之间的合作关系,本文选取网络中的极大连通子图;Email[23]网络是电子邮件收发网络,联系人之间发送过邮件产生一条边;Blogs[23]网络是MSN上的博客网络,当一个人在另外一个人的博客有评论时,产生一条边。上述网络均按照无向无权网络处理,<k>表示网络平均度,即网络中所有节点度的平均值,kmax表示节点最大度,<d>表示网络节点间最短路径平均数,C表示聚类系数,用来评估节点聚集成团的集聚程度;R表示同配系数,用来反映邻接节点间的度相关性;H表示异质系数,衡量网络中节点度分布的异质[24~25]。β表示SIR传播模型中的感染概率。
表3展示了ks、Cnc+、EKsd、DK及本文提出的两种确定权重方法GDI和EDI分别在上述六个数据集仿真实验进行关键节点识别,排序结果的单调性分析,由表可知,k-shell方法在三个数据集上的单调性验证结果均是最差,存在粗粒化划分问题。本文提出的使用到最大核节点的距离改进迭代次数,两种权重赋予方式提出的GDI、EDI方法单调性验证结果排名Top2,且GDI单调性优于EDI。说明两种赋予权重的方法均能够有效地解决k-shell划分结果粗粒化的问题,使得更多的节点被划分到不同的等级。

表3 不同度量节点单调性分析表
表4展示了ks、Cnc+、EKsd、DK、GDI和EDI算法分别在六个数据集的关键节点识别结果,与SIR仿真传播确定节点传播能力的节点重要性之间的相关性,通过数学计量Kendall相关系数体现相关性差异,本文算法EDI在六个数据集上均与SIR传播模型相关系数值最大,相关性最强,最贴近标准排序结果。EDI算法在DK算法基础上考虑节点到最大核节点的平均距离,改进K核迭代次数,使用熵权法确定权重,在上述六个数据集中,单调性和有效性均优于其他算法。GDI算法使用灰色关联度分析法确定权重进而计算节点重要性指标,但是从表4算法有效性中看出,该方法在部分数据集上优于相同贡献度的EKsd算法、熵权法确定权重的DK算法,如karate数据集、net Science数据集,在部分数据集上与SIR传播模型标准排序差异很大,如Blogs网络。因为在使用灰色关联度分析法确定权重时,对于所有网络人为主观决定分辨系数ρ取定值0.5,取值的不同会最终影响权重的分配,使得算法可信度降低。所以采用熵权法确定权重可以更有效地进行关键节点识别。
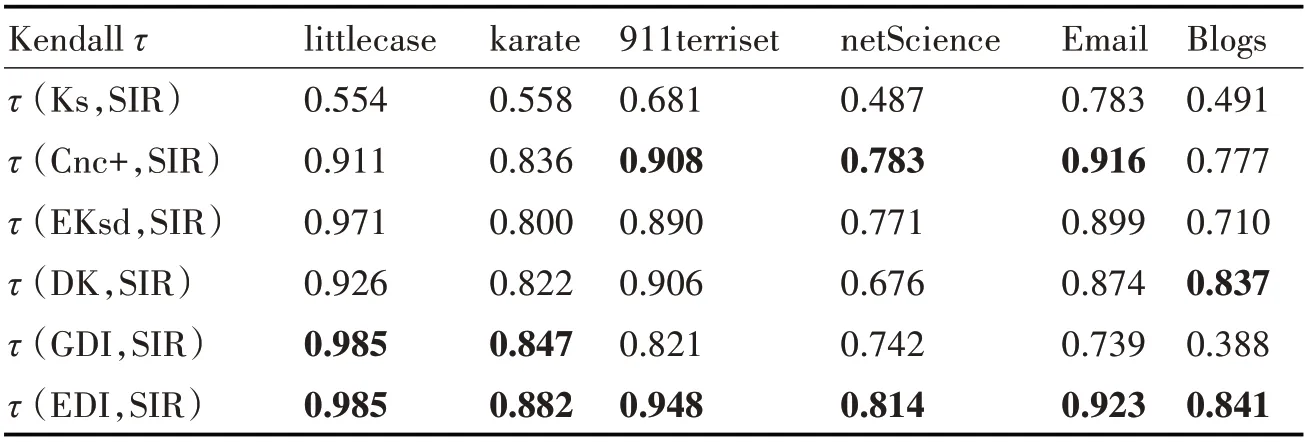
表4 不同度量指标相关性分析表
5 结语
本文算法主要解决复杂网络中关键节点识别问题中,k-shell识别方法带来的粗粒化划分问题,融合网络局部信息和全局信息,更全面地识别网络中的关键节点,通过节点到最大核距离改进K核迭代次数、融合节点度,使用熵权法确定权重,结合邻居节点的贡献,更有效地识别无向无权网络中的关键节点。实验证明,GDI算法虽然在单调性方面明显优于其他方法,但EDI算法在有效性上明显优于其他方法,能够以较高精度识别出网络中的关键节点。下一步计划将点权强度融合到本文算法扩展到加权网络,进一步对灰色关联度分析方法中的参数ρ进行深入研究。

