CBD模型对高年龄段死亡率的预测

吕聪慧 王永茂

摘 要：人口老龄化现象发生在我国日益显著，因此我们越来越多地关注对于死亡率的研究，而对高年龄段老龄人口的死亡率研究则更加显得重要，CBD模型恰恰适合于高年龄段的人群的死亡率预测。本文针对全国分年龄段人口死亡率历史数据，预测出未来10年的年龄人口死亡率及趋势。

关键词：人口老龄化;CBD模型;死亡率

0 引言

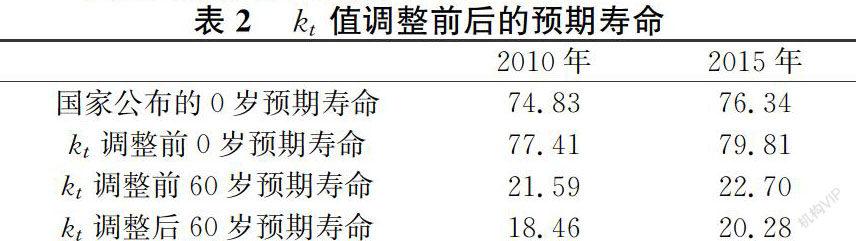
在参考官方提供的预期寿命时，要考虑到官方的预期寿命是0岁人口的预期余寿，而要想得到60岁人口的预期寿命，需要进一步计算才可以。第一步就是根据官方提供的出生人口的预期寿命调整Lee-Carter模型的时间因子，并据此估计60岁人口的预期余寿，利用这一结果再对CBD模型的时间因子进行调整。

1 模型介绍

1.1 Lee-Carter模型

Lee和Carter提出了国内外学者所周知的动态死亡率模型Lee-Carter模型，这个模型综合考虑了年龄和时间两个因素的影响，模型的表达式如下：

1.2 CBD模型

Carins-Blake-Dowd关系模型（以下具体简称模型CBD关系模型）主要定义指的也就是结合Carins，Blake和Dowd在2006年之后首次正式提出的两种多因素关系模型，模型的描述形式及其描述主要如下：

死亡率值经过logit变换后呈现出线性趋势。q（x，t）代替m（x，t）是用来表示一个日历年t年龄大于x岁的一个人在 t +1年之前发生死亡的可能性和概率，但是，m（x，t）和q（x，t）差别极微，所以用m（x，t）代替q（x，t）。x-表示年龄的均值，（k（1）t，k（2）t）为时间序列。

2 Lee-Carter模型参数估计

本文所涉及的数据主要是从2010-2019年《中国人口和就业统计年鉴》中提取。

本文求解Lee-Carter模型参数的方法是最小二乘法。

3 调整Lee-Carter模型的时间因子

调整目标是预期寿命，固定α∧x和β∧x，只对kt的值进行调整，使得调整后的Lee-Carter模型的人群预寿同于国家发布的。调整后2010年Lee-Carter模型的kt值，即k2010=16.34;2015年Lee-Carter 模型的kt值，即k2015=-8.93。

从图1中可以看出，年份相同的情况下，随着年龄的增长，死亡率的对数值逐渐增大，意味着死亡率逐渐增大;而在同一年龄，随着时间的递增，死亡率的对数值逐渐减小，意味着死亡率逐渐降低。

参考文献

[1]苏雯.不规则数据下中国城市人口死亡率CBD模型的估计、预测与应用[D].北京：华北电力大学，2019.

[2]何兴凤，郑静，张桂军，等.Lee-Carter模型在新农保中的应用[J].杭州电子科技大学学报（自然科学版），2014，34（06）：80-83.

[3]Cairns A.J.G.Blake D.Dowd K.A two-factor model for stochastic mortality with parameter uncertainty：theory and calibration[J].Journal of Risk and Insurance，2006，（73）：687-718.

[4]曾燕，陳曦，邓颖璐，等.创新的动态人口死亡率预测及其应用[J].系统工程理论与实践，2016，36（07）：1710-1718.

[5]Ermanno Pitacco，Michel Denuit，Steven Haberman，Annamaria Olivieri.Modelling Longevity Dynamics for Pensions and Annuity Business[M].Oxford：Oxford University，2009.