土壤重金属砷的高光谱估算模型
李志远, 邓 帆, 贺军亮, 魏 薇
1. 长江大学地球科学学院,湖北 武汉 430100 2. 石家庄学院资源与环境科学学院,河北 石家庄 050035
引 言
土壤重金属监测在农业生产中至关重要, 尤其工业和农业密集地区存在重金属扩散到食物链的风险[1]。 砷(As)是人体所需微量元素之一, 但若吸入出现超标, 会对人体健康造成极大危害。 含砷三废的排放和农药化肥的过度使用人为加剧了重金属砷污染[2]。
传统的土壤特性检测方法能够准确测得重金属含量, 但是花费高、 步骤繁琐、 耗时长, 无法做到实时高效[3]。 高光谱技术具有成本低、 效率高、 用时短等特点, 被广泛用于重金属含量估算研究中[4]。 目前, 用于土壤重金属As高光谱反演的线性建模方法主要有单变量回归、 多元线性逐步回归、 主成分回归、 偏最小二乘回归、 地理加权回归等, 这些方法在对应的研究区域取得了较好的效果。
多元线性逐步回归(multiple linear stepwise regression,MLSR)和偏最小二乘回归(partial least squares regression,PLSR)在估算重金属As含量中运用非常普遍, 它尽可能选出对重金属As含量影响较大的自变量, 但是容易出现过度拟合情况, 导致模型稳定性降低[5]; 偏最小二乘回归综合了主成分回归和多元线性逐步回归方法, 能够在波段个数较多且自相关严重时建立回归模型, 避免共线性问题[5]。
以采矿地和冶炼企业较多的石家庄市地表水源地保护区褐土为研究对象, 主要根据重金属As含量与光谱指标进行相关分析选出特征波段, 运用多元线性逐步回归和偏最小二乘回归方法来估算土壤重金属As含量, 找出反演重金属As的优选方法, 对研究该区域土壤As污染的快速监测提供借鉴。
1 实验部分
1.1 研究区概况
研究区位于石家庄市滹沱河中游的平山县和井陉县境内, 主体(一级保护区)包括滹沱河干流、 黄壁庄水库和岗南水库及其支流, 主体外设有二级和三级保护区(如图1)。 总体呈西北向东南逐渐降低, 地势差距较大。 由于样本采集区域开发较早, 人地矛盾突出, 矿产的开采造成了土壤重金属污染问题, 对研究区现有生态安全造成一定的负面影响[6]。

图1 研究区和土壤采样点分布图Fig.1 Study area and the distributionof the soil sampling points
1.2 样本采集
基于研究区地形和土壤空间分布不均匀的特性, 依据研究区内主要采矿点和冶炼企业的分布, 按照地表径流路径设置三条样带, 采集土壤样本48个, 采集深度为0~20 cm, 同时使用GPS定位, 采样点位置如图1所示。 采集的所有土壤样本带回室内, 经风干、 研磨、 过100目筛, 变成粉状土, 然后将每份样本一分为二, 分别进行土壤基本理化性质和高光谱数据的测定。 采用微波消解仪(CEM-Mars)消解, 利用电感耦合等离子体质谱仪(PE-Nexion 300 ICP-MS)测定土壤中的砷含量全量。 表1为48个土壤样本中砷含量的描述性统计值。

表1 土壤中砷含量的描述性统计值(mg·kg-1)Table 1 Descriptive statistics of the arseniccontent (mg·kg-1) in soil
研究区土壤中重金属As含量分布在10.844~15.125 mg·kg-1之间, 平均值为13.230 mg·kg-1, 接近河北省背景值[7], 说明采集的部分土壤样本中重金属As含量已经富集到了一定程度。 土壤重金属污染程度采用单因子评价法[8]来分析, 计算公式为
Pi=Ci/Si
(1)
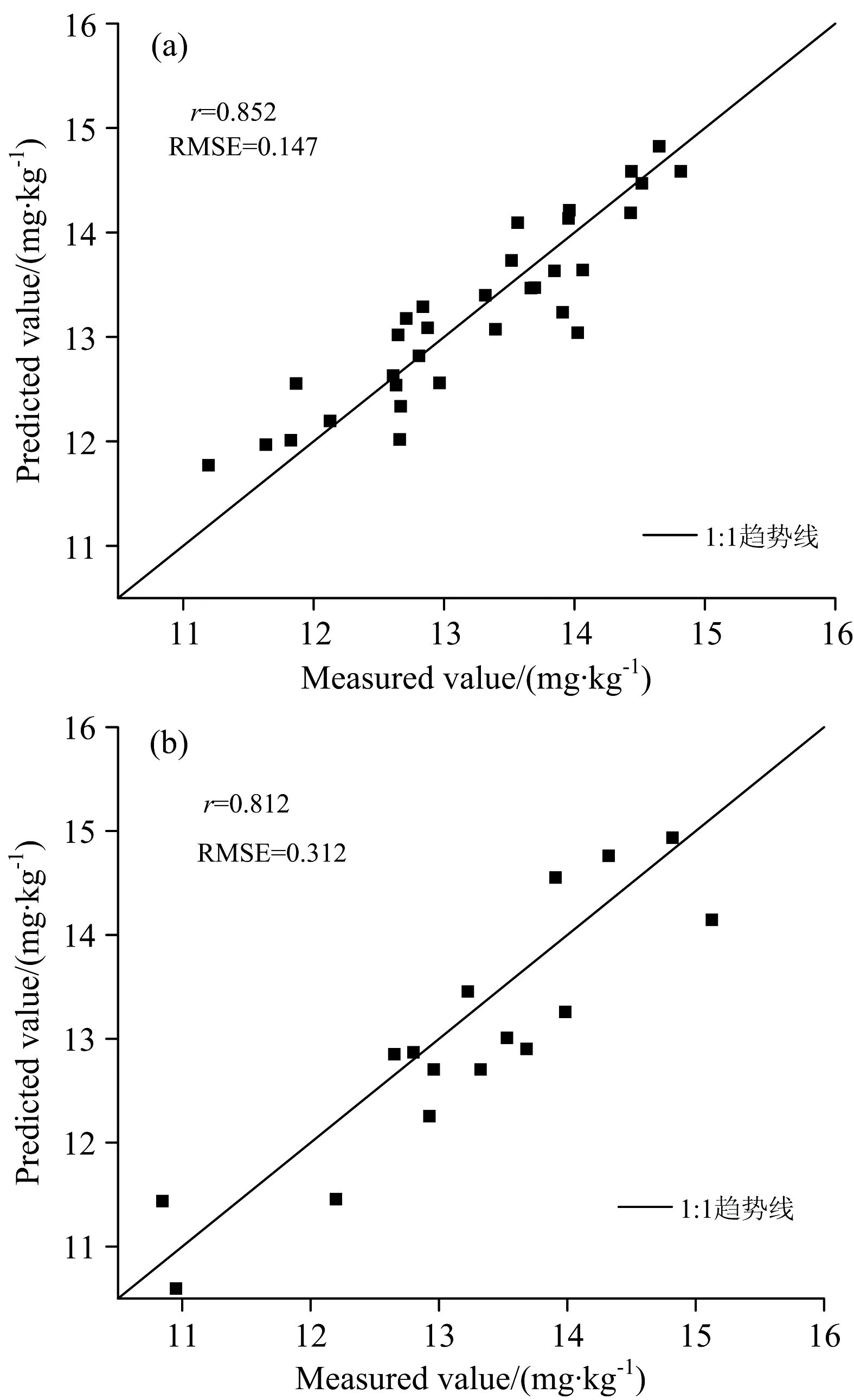
其中Pi表示土壤中重金属As的污染指数, Ci表示土壤中重金属As的实测值, Si表示土壤中重金属As的河北省背景值。 Pi≤0.7为安全范围, 0.7 由表2统计得到, 污染指数的最小值为0.797, 平均值为0.973, 最大值为1.112。 有29个样点处于警戒范围; 有19个样点受到重金属As的轻度污染[9]。 综合看来, 约40%土壤样本受到重金属As的轻度污染, 受到了采矿点和冶炼企业的影响, 有必要对重金属As含量进行长期动态监测。 表2 土壤中砷的单因子污染指数统计结果Table 2 Statistical results of single factorpollution index of the soil arsenic 采用FieldSpec Pro便携式光谱仪测定土壤光谱反射率, 波段范围为350~2 500 nm, 采样间隔为1.4 nm(350~1 000 nm)和2 nm(1 000~2 500 nm), 重采样间隔为1 nm。 光谱测量在可调节光照的暗室内进行, 为尽可能减少外来光线的影响, 选用卤素灯作为唯一光源。 将处理好的土壤样本放入玻璃培养皿(直径10 cm、 深2 cm)内, 置于黑色绒布上, 用工具将土壤表面刮平。 光源天顶角为45°, 距土样表面30 cm, 探头置于距土壤样本表面垂直上方的15 cm处, 光纤探头视场角为5°。 每次测试前进行白板标定, 每个土壤样本测试10次光谱曲线, 取算数平均值作为该样本实际光谱数据。 为消除仪器信噪比、 样本风干和杂散光等因素的影响, 采用Savitzky-Golay 7点平滑, 去除噪声较大的异常波段, 保留1 640个波段用于后续建模研究。 为了提高光谱信噪比, 去除背景噪声, 突出光谱特征, 通过原始光谱反射率(SR)分别计算一阶微分(FD)、 二阶微分(SD)、 倒数(RT)、 倒数一阶微分(RTFD)、 倒数二阶微分(RTSD)、 倒数对数(AT)、 倒数对数一阶微分(ATFD)、 倒数对数二阶微分(ATSD)、 连续统去除(CR)。 将重金属实测值与以上经光谱变换后的数据进行相关性检验, 得到相关性最高的波段。 光谱变换由Origin2020b和ENVI5.1软件进行, 结果见图2。 相关性分析及后续模型建立在Minitab18软件中完成。 图2 光谱变换后的土壤样本光谱反射率曲线Fig.2 Transformed soil reflectance spectra after (1) MLSR 多元线性逐步回归是通过一个因变量和多个自变量组合表达它们之间的线性关系。 回归方程为 y=β0+β1x1+β2x2+…+βkxk+ε (2) 其中, y表示因变量, x表示自变量, βi(i=0,1,2,…,k)表示回归系数, ε表示随机误差, k表示自变量的数量[10]。 将土壤重金属As实测含量作为建模样本的因变量, 将光谱指标作为自变量, 根据贡献率高低来建立MLSR模型。 (2) PLSR 偏最小二乘回归是一种结合主成分回归和MLSR的分析方法, 由Herman Wold于1966年提出, 目前已被广泛应用于光谱数据处理。 PLSR的主要研究内容是在大量的两组高线性相关变量的情况下, 建立自变量的线性模型, 以解决样本数小于变量数的问题, 避免出现过拟合, 因此PLSR是对MLSR的改进。 PLSR的原理是: 首先从自变量(x1,x2,…,xm)中提取相互独立的分量Th(h=1,2,…), 并且提取的主成分携带尽可能多的原始成分; 然后从因变量(y1,y2,…,ym)中提取独立分量Uh(h=1,2,…), 要求Th和Uh之间的协方差最大化, 并利用MLSR得出的因变量建立回归模型。 偏最小二乘回归的基本模型是 X=ThPT+E (3) Y=UhQT+F (4) 其中,P和Q分别是m×h的正交载荷矩阵,E和F是误差项(服从正态分布的随机变量)[11]。 以土壤重金属As实测含量为因变量, 选用单一光谱指标的特征波段作为自变量建立单光谱变换指标偏最小二乘回归(univariate partial least squares regression,U-PLSR)模型, 用MLSR筛选出的多种光谱指标作为自变量建立多光谱变换指标偏最小二乘回归(multivariate partial least squares regression,M-PLSR)模型。 随机将48个样本分为两部分, 32个用作建立模型, 16个用来验证模型。 采用相关系数r、 均方根误差(root mean square error,RMSE)和统计值F来衡量建模效果。F值和r越大, RMSE越小, 建模样本和验证样本的散点分布越靠近1∶1线, 建模效果越好, 由此确定最佳回归模型。 原始光谱曲线经过平滑之后得到的曲线如图3所示, 48个土壤样本的光谱曲线形态基本相同。 在可见光波段, 光谱反射率随波长增长而增大, 在近红外波段, 整体趋于平缓。 光谱曲线在600和800 nm附近有机质的反射峰; 1 400, 1 900和2 200 nm波段附近存在三处明显的水分吸收带, 这是受到土壤中硅酸盐矿物和粘土矿物有关[12]。 FD, SD和ATFD变换光谱曲线起伏较大; RT和AT变换呈现从起始波段迅速下降, 到600 nm附近降幅变缓趋势; RTFD, RTSD和ATSD变换后反射率变化主要出现在500 nm之前; 经CR变换, 光谱曲线归一化在0~1之间, 吸收谷出现在500, 1 010, 1 400, 1 900和2 200 nm附近(图3)。 图3 平滑后的土壤样本光谱反射率曲线Fig.3 Smoothed reflectance spectra of soil samples 为了探究不同光谱指标与重金属砷含量的关系, 将As含量与各种光谱变换进行Pearson相关性分析, 表3表示最大相关系数及其对应的敏感波段。 表3 土壤重金属砷含量与光谱指标的最大相关系数Table 3 Maximum correlation coefficients of heavymetal As content and spectral indexes 可以发现, 经CR光谱变换后682 nm与重金属As含量的相关系数出现明显峰值, 达到0.603(如图4), 这可能与重金属As受到土壤有机质的吸附有关。 FD的1 211 nm与土壤重金属As含量存在最大负相关性。 其中通过0.01(双尾)显著性检验的波段还有SD和ATSD的2 208 nm、 RTSD的1 065 nm、 ATFD的464 nm, SR的2 342 nm, 相关系数均超过0.370, 表示相关性显著, 而RT和AT的1 740 nm相关系数大于0.28, 通过了0.05(双尾)显著性检验, 表示相关性比较显著。 RTFD未能通过任何相关性检验, 因此在最后建立模型时不予考虑。 图4 连续统去除相关系数曲线图Fig.4 Continuum removal correlation coefficient curve MLSR是筛选对因变量影响较大的自变量建立回归模型的方法。 根据自变量对因变量的作用大小, 剔除不显著的自变量, 由大到小逐个引入回归方程, 由于考虑了多个变量因素, 建模结果具有一定的可靠性。 根据土壤重金属砷含量与光谱指标的相关分析, 将表3中各光谱指标对应的敏感波段作为As含量估算模型的自变量, 以As实测值为因变量, 建立MLSR模型。 通过建模分析, 将FD1 211, RTSD1 065, ATFD464和CR6824个对模型拟合度影响较大的光谱指标保留。 具体模型为 Y=-638.304-6 629.954XFD+1 110.784XRTSD- 391.284XATFD+651.907XCR (5) MLSR模型的散点图和验证结果如表4和图5所示, 建模样本r超过0.8, 基本分布在1∶1线两侧, 说明该模型对建模数据具有良好的解释能力。 而验证样本数据分布相较于建模样本距离1∶1线存在较大偏离, 说明模型预测效果不如建模效果, 模型稳定度需要进一步探究。 表4 MLSR模型结果Table 4 Results of MLSR model 图5 MLSR模型建模样本和验证样本散点图(a): 建模样本; (b): 验证样本Fig.5 Scatter plots of fitting and testing sets for MLSR(a): Fitting set; (b): Testing set 依照2.3分析, 将筛选出来模型精度影响较大的光谱指标(FD1 211, RTSD1 065, ATFD464和CR682)分别作为自变量, 构建U-PLSR模型。 为避免发生过度拟合现象, 采用逐一剔除法进行交叉验证(下同)。 U-PLSR模型结果见表5。 表5 U-PLSR模型结果Table 5 Results of U-PLSR model 依照模型的r和F值最大, RMSE最小原则, 经CR光谱变换的建模和验证效果最好, 其次是FD, ATFD效果最差。 相比MLSR建模结果, 4种U-PLSR模型的r均较低, 最高仅达到0.381, 这表明U-PLSR模型稳定性较差, 不能做到准确有效的估算重金属As含量。 基于MLSR和U-PLSR模型, 为了寻找更为稳定的模型, 进一步建立M-PLSR模型, 所用模型光谱指标和MLSR模型相同。 M-PLSR模型的散点图和验证结果如表6和图6所示, 具体模型为 图6 M-PLSR模型建模样本和验证样本散点图(a): 建模样本; (b): 验证样本Fig.6 Scatter plots of the two set of samplesof fitting and testing for M-PLSR(a):Fitting samples; (b): Testing samples 表6 M-PLSR模型结果Table 6 Results of M-PLSR model Y=-690.390-6 011.343XFD+1 174.766XRTSD-391.829XATFD+643.903XCR (6) 建模样本和预测样本均超过0.8, 分布更为均匀, 相较于MLSR模型更靠近1∶1线。 M-PLSR模型的建模样本r,F值和RMSE分别达到0.852, 32.384和0.147, 验证样本r为0.812,F值为8.598, RMSE为0.312, 比MLSR模型相比, 建模r增加0.038,F值增加2.947, RMSE降低0.012, M-PLSR建模效果好于MLSR, 预测模型也有所提升。 综合来看, M-PLSR模型拟合度更高, 建模效果更佳, 模型稳定度也更强, 更适合用于估算研究区重金属砷含量。 通过实地采样分析, 研究区重金属As含量平均值为13.230 mg·kg-1, 接近河北省背景值。 采矿和冶炼企业对土壤重金属As含量有一定影响, 使得部分土壤样本As含量已经存在轻度污染情况, 大部分样本略低于背景值, 处于污染的警戒水平。 研究区域和土壤背景的不同使得重金属As的特征波段存在差别。 某矿区农田潴育性水稻土重金属As的特征波段有450, 700, 1 200和2 200 nm等[13]; 三江源地区以高山草甸土和高山草原土为主的特征波段为400, 429, 470, 550, 600, 815, 900, 1 415, 1 915, 2 205, 2 355和2 455 nm等[12]; 商洛黄褐土的特征波段包括450, 470, 640~660, 1 030~1 060, 1 080~1 110, 1 230和2 190~2 220 nm等[11]。 这些特征波段与本研究所得结果基本一致(464, 682, 1 065, 1 211和2 208 nm), 但并不完全相同, 其中本研究与商洛黄褐土重合率最高, 可能因为两种土壤类型相似性较高。 土壤重金属As含量的研究多采用单光谱变换指标建模, 突出单一光谱指标的特征, 模型可能存在误差。 本工作选用了10种光谱指标, CR与土壤重金属As含量相关性最高, 且在U-PLSR模型中CR建模效果最好, 这主要是因为CR能够有效的消除研究区潜在因素对光谱的影响, 可以增强光谱对As的敏感性。 多光谱变换指标集成建模结合多种最佳特征波段, 一定程度上避免了单一光谱指标的不足, 达到提升建模效果和模型稳定性的目的。 重金属估算模型受到区域位置和土壤类型甚至污染水平的影响, 构建的最佳模型是否适用其他土壤类型和其他地区土壤还有待深入研究。 针对石家庄市水源地保护区褐土重金属As含量的高光谱估测, 通过相关分析, 建立了土壤重金属砷含量MLSR, U-PLSR和M-PLSR估测模型, 具体结论如下: (1)重金属As与经连续统去除变换后的光谱特征的相关性最大, 达到0.603, 与一阶微分含量存在最大负相关性, 达到-0.527。 (2)相较于MLSR和U-PLSR, M-PLSR方法估算土壤重金属As含量建模和验证样本的r分别达到0.852和0.812, 模型预测值和重金属As实测值整体拟合度最高。 (3)多光谱变换指标建模效果显著, 相比单光谱变换指标模型, 它的建模结果和预测能力表现更好, 可以对估算重金属As含量起到较好的作用。
1.3 光谱测定
1.4 光谱数据预处理

1.5 多变量反演方法
1.6 模型建立与检验
2 结果与讨论
2.1 研究区土壤光谱特性

2.2 特征波段提取
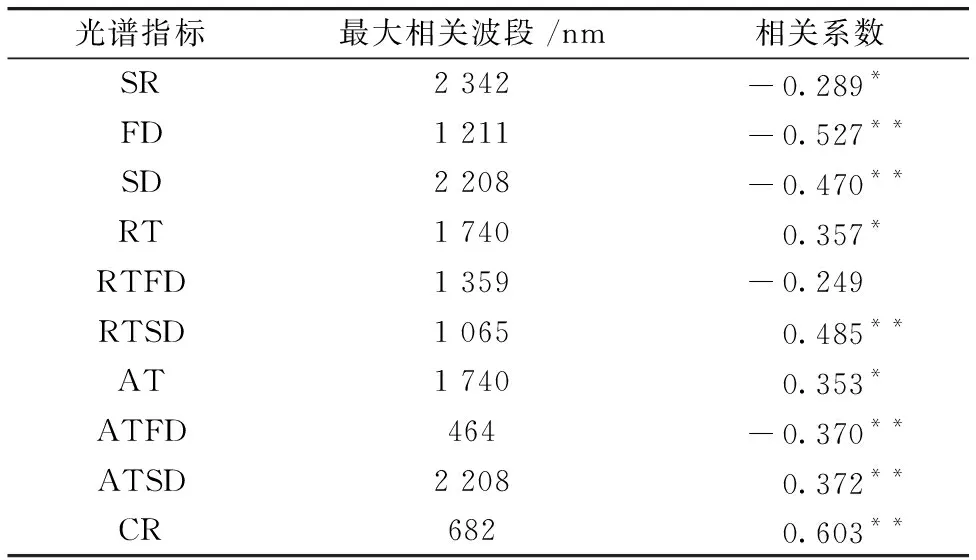
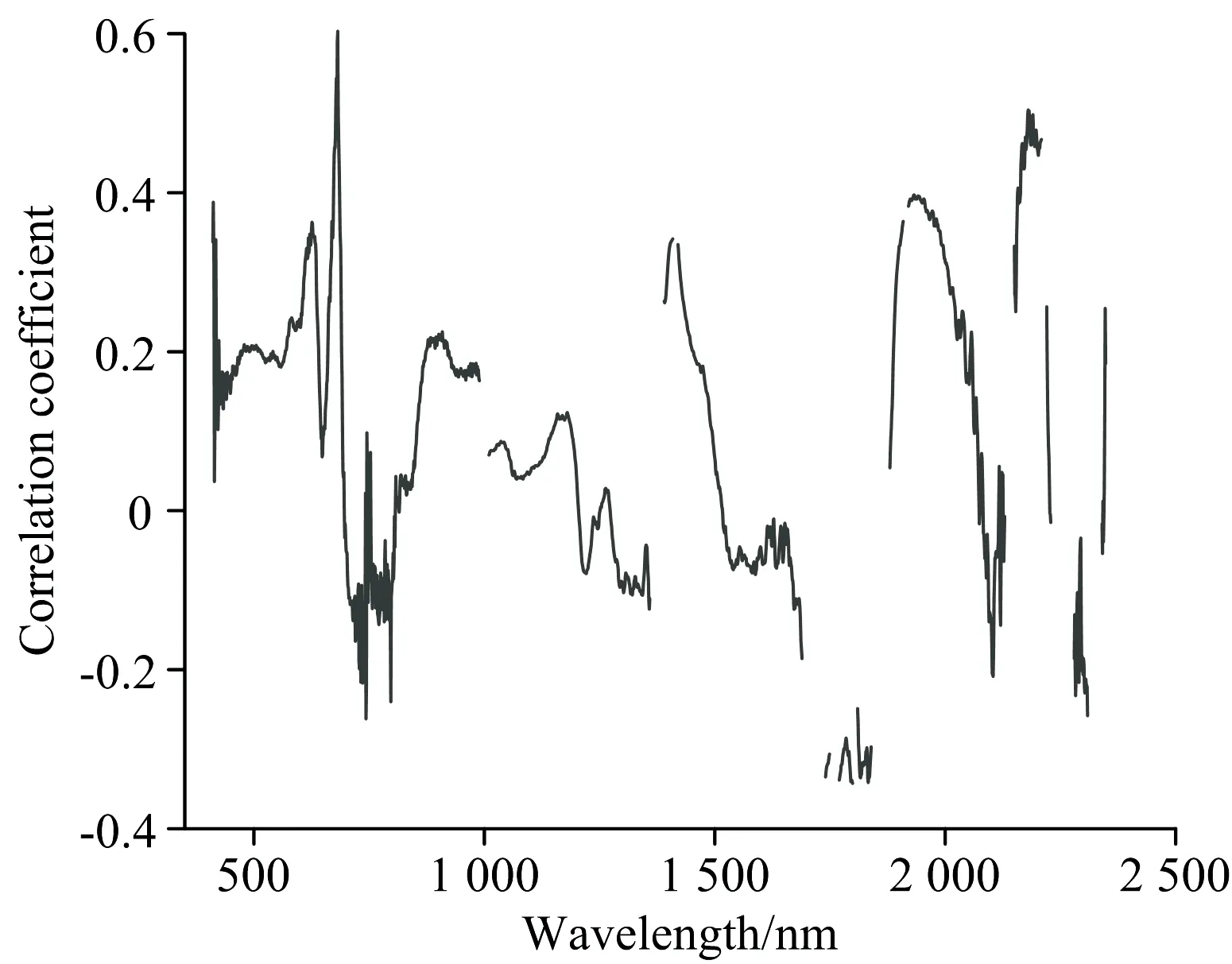
2.3 MLSR
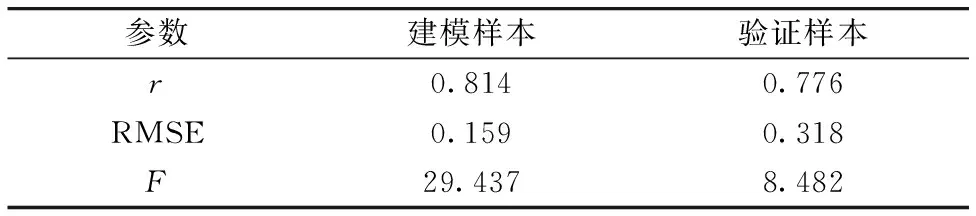
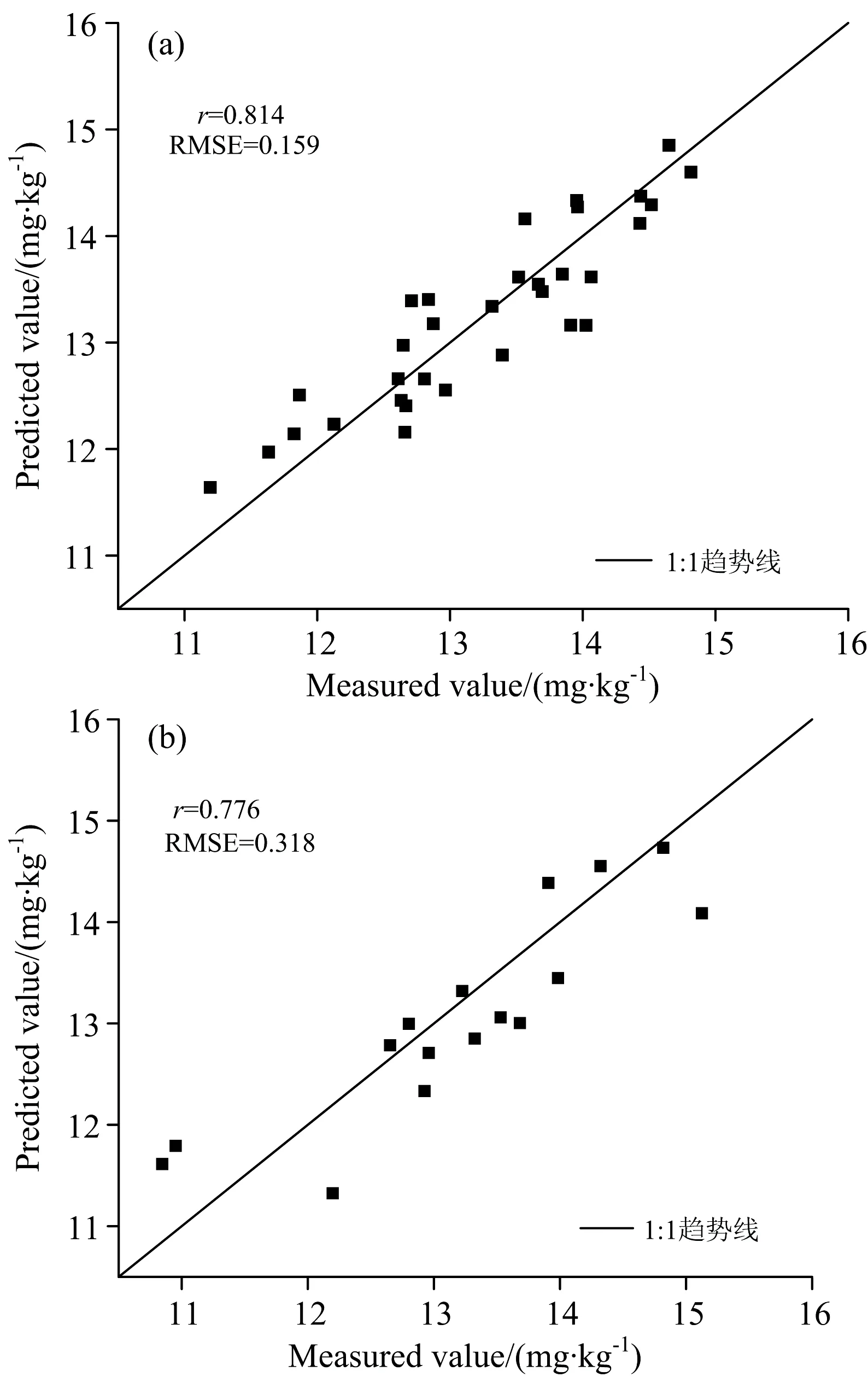
2.4 U-PLSR

2.5 M-PLSR

3 结 论
——与非适应性回归分析的比较

