外后视镜镜壳造型对气动噪声影响研究

叶 佳，夏之祥，朱茂桃，徐 明，邢 鹏

(1.江苏大学 汽车与交通工程学院， 江苏 镇江 212013；2.上汽大众汽车有限公司 产品研发部， 上海 201805；3.上海干巷车镜实业有限公司 产品研发部, 上海 201518)

噪声是衡量汽车性能的重要指标。汽车行驶时，噪声主要有发动机噪声、轮胎噪声和气动噪声。随着车速的增加，气动噪声的影响越发显著，对乘车舒适性有较大影响。后视镜是凸出于汽车外表面的钝体结构，其造型特征对车内气动噪声的影响较大[1]。

对后视镜气动噪声产生机理和影响因素的研究主要集中在3个研究方案：第一，平板模型，即将后视镜安装在平板上进行研究，Chen等[2]将GMT360和GMX320两款后视镜安装在试验台架上单独研究后视镜气动噪声的影响因素；第二，Ahmed模型，对安装在楔形体上的后视镜进行研究，杨博[3]采用子域法对Ahmed模型上的后视镜进行研究，分析后视镜尾流场特征和侧窗表面气动噪声声压级水平，大幅减小了仿真计算量；第三，整车模型，研究安装在整车上的后视镜，Haidong Y等[4]对比了楔形体、后视镜-平板和整车模型3种安装环境对后视镜周围流场的影响，结果表明整车模型计算结果更可靠。目前，国内外研究机构对后视镜气动噪声的研究已取得一些成果。为了解后视镜气动噪声产生机理，袁海东等[5]利用风洞试验研究类后视镜尾迹特征，将后视镜尾部流场可视化，明确了后视镜尾部涡流以大尺度脱落涡为主。对于后视镜外形优化的研究，李启良等[6]以类后视镜模型为基础，研究了后视镜不同外形参数对于后视镜气动噪声的影响。陈鑫等[7]通过风洞试验和数值模拟研究了后视镜凸起位置以及基座造型对气动噪声的影响。这些研究结果表明，造成后视镜气动噪声的主要原因是旋涡不断地从后视镜表面交替产生并脱落，引起周围空气压力脉动，作用在前侧窗区域产生气动噪声。

综上所述，国内外多使用类后视镜-平板模型研究基本造型因素的影响，而基于真实后视镜造型因素对气动噪声影响的研究并不多。为此，从真实后视镜模型入手，采用整车模型，通过数值模拟和风洞试验研究后视镜尾部流场和气动噪声，合理优化后视镜镜壳造型，控制尾涡区域，引导尾涡走向，从而减小后视镜尾涡对前侧窗表面气动噪声的影响。

1 气动噪声理论

流体的流动遵从质量守恒和动量守恒定律[8-9]。数学表达式如下：

(1)

(2)

式中：ρ为流体密度；p为微元体上的压力；u为流体速度矢量。

1952年，Lighthill[10-11]在流体运动方程的基础上提出了著名的Lighthill方程，首次揭示了流场参数和声场之间的关系。该方程建立在理想流场环境中，数学表达式为：

(3)

(4)

式中：Tij为Lighthill张量；p-p0为压力波动值；ui和uj为速度分量；δij为单位张量；c0为声速；ρ-ρ0为流体密度差值。

Curle拓展了Lighthill声类比理论，将其运用到存在静止固体边界的流场中，得到Curle方程[12]：

(5)

式中：n为固体表面法向向量；r为由固体表面指向监测点的向量；S为固体表面。

FW-H方程进一步将Curle方程扩展到运动固体边界的流场中[13]，其方程式为：

(6)

式中：δ(f)为δ函数；Pij为压应力张量；τij为黏性应力张量。方程左边描述的是声音的传播项，右边表示的是声源项。第1项为加速度引起的单极子声源项，第2项为由湍流作用造成表面压力脉动引起的偶极子声源项，第3项为四极子声源项。

Howe在FW-H方程的基础上进行简化，推导出低马赫数等熵流动的Howe涡声方程[14-15]：

(7)

式中：B为流体总焓；P为压强；u为速度矢量；ρ为流体密度；ω为流动涡矢量；c0为声速。方程左边描述了声音在非均匀流动介质中的传播，右边为气动声源产生项。涡声方程表明气动噪声产生于流场中涡的伸缩和破裂，即只有存在涡的地方，才会产生气动噪声[16]。

2 数值仿真

2.1 几何建模及确定计算域

采用某SUV真实后视镜为基本模型，运用CATIA软件修改镜壳造型。原模型为镜壳迎风面低于镜圈结构，如图1所示。模型1为镜壳迎风面与镜圈齐平后视镜模型，模型2为镜壳迎风面高于镜圈后视镜模型。

图1 3种外后视镜几何模型示意图

为节约计算资源、排除其他因素的干扰，对整车模型进行简化。采用四分之一车模型，并简化车轮、行李架和进气格栅等部件。为保证数值仿真和风洞试验结果的一致性，仿真计算域的长、宽和高分别对应于车身尺寸的9倍、4倍和5倍，如图2所示。

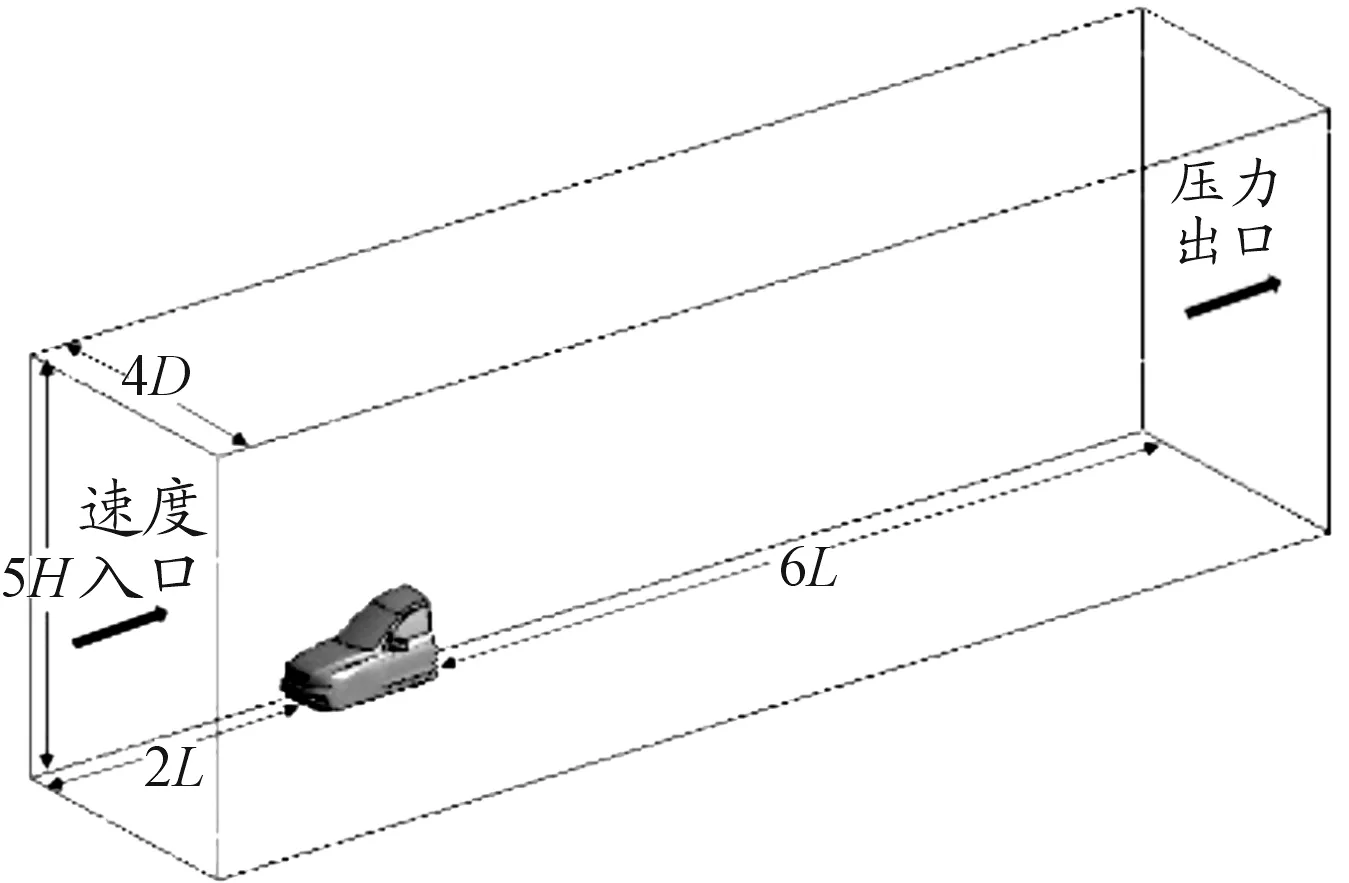
图2 计算域模型示意图

2.2 网格划分

将模型分为不同的网格尺寸，A柱-后视镜区域为重点关注对象。网格尺寸会影响声学计算精度，因此对此区域进行网格局部加密，最小面网格尺寸为2 mm，车身最大面网格尺寸为8 mm，计算域壁面最大面网格尺寸为256 mm。根据面网格拉伸生成10层边界层，第1层高度为0.02 mm，增长率设置为1.2，总高度为0.63 mm。边界层网格划分完成后，在边界层和计算域间生成四面体网格，共约2 700万个网格。稳态计算时，选用Realizablek-ε湍流模型，该模型对于有大逆压梯度的边界层、分离和回流现象有较好的预测结果。入口处湍流强度设置为2.5%，离散格式为较高精度的2阶迎风格式。仿真计算时，由于车尾距离风洞出口具有充足的距离，可以认为气流为完全发展的不可压缩流动，因此出口边界条件设置为压力出口，表1为边界条件设置。后视镜尾部流场中以大尺度脱落涡为主[17]，因此为了准确模拟后视镜引起的气动噪声，瞬态计算时，湍流模型选择大涡模拟(LES)的计算方法。亚格子应力模型为Smagorinsky-Lilly模型。

表1 计算域边界条件

为使非定常流场计算更容易收敛，先进行稳态计算得到定常流场，并作为初始值用于求解非定常流场。在求解外声场时，时间步长应与非定常流场求解的时间步长一致。根据斯特劳哈尔数计算设置为0.000 02 s,采样时间设置为0.2 s，为后视镜流场特征周期的10倍。

3 整车风洞试验

为了验证数值模拟结果的可靠性，该款车模型的整车气动噪声试验在同济大学的上海地面交通工具风洞中心完成。为保证仿真计算和试验条件一致，车身表面连接部位(包括前进气格栅、门窗、门把手等)采用胶带全密封。在前侧窗表面布置GRAS公司生产的表面传声器测量侧窗表面脉动压力和声压。表面传声器上装有导流罩，减少“自噪声”对试验结果的干扰，采用HEAD公司的测试系统进行数据采集和分析。

由于该车型后视镜安装角度左右侧完全对称，且车身沿中间对称面两侧对称，因此只在驾驶员侧的侧窗表面布置监测点，共4个监测点，如图3所示。试验时，温度稳定在24 ℃左右，湿度为82.7%，试验风速为38.9 m/s(即140 km/h)，车辆偏航角为0°。风洞试验和表面传声器监测点分布见图3。

图3 风洞试验和表面传声器监测点分布示意图

图4中分别对侧窗上4个监测点的计算和试验的A计权声压级结果进行比较。结果表明，仿真与试验结果最大误差为4.3 dBA，且每个测点有超过80%的频率下数值计算与试验结果误差在3 dBA范围内。由图4可见：各监测点的计算结果和试验得到的声压级频谱图变化趋势一致，因此可认为该数值模拟方法是合理正确的。

4 数值仿真结果分析

4.1 稳态流场分析

汽车高速行驶时，外后视镜表面边界层从后部发生分离，在其尾部形成类似于卡门涡街结构的旋涡。旋涡产生和周期性脱落，并向其后方发展，引起周围空气压力波动，作用在前侧窗表面产生气动噪声[19]。为探究不同后视镜镜壳造型对其尾部流场的影响，建立XOY,XOZ和YOZ平面对稳态计算结果进行分析，如图5所示。

图5 3个平面示意图

通过比较3种后视镜尾部的流线图可以看出：由于镜壳造型不同，后视镜尾部区域的流态是有差异的。从图6中可以看出：在XOY平面上，原模型和模型1都存在2个涡流中心，模型1上方的旋涡较小，下方旋涡流线稀疏，涡流强度较小；模型2后方只有1个涡流中心，且涡流尺度较小。在XOZ平面上，后视镜尾部存在2个旋转方向相反的旋涡，模型1上方旋涡尺度相比于原模型有所减小，且流线稀疏；而模型2后方两个涡流尺度都相对较小，尾部涡流区面积减小，且上方旋涡有远离侧窗表面，往车门方向引导的趋势。在YOZ平面上，3个模型后方都有两个涡流中心，模型1的涡流尺度相比于原模型有所减小，而模型2后方的涡流中心沿侧窗外法线方向移动，远离侧窗表面，减小涡流对侧窗表面的作用，降低侧窗区域气动噪声。

图6 3个平面上流线图

综上所述，由于后视镜上方镜壳造型结构不同，改变了镜壳表面气流的速度和角度，对后视镜尾部气流走向具有引导作用，使其尾部涡流中心沿远离侧窗表面方向移动。根据涡声理论，涡流是产生气动噪声的主要原因，后视镜尾部涡流尺度越小，离侧窗表面越远，越有利于降低前侧窗区域气动噪声。根据上述分析，模型1和模型2对改善后视镜区域流场有积极作用，有利于降低该区域气动噪声。

为详细研究后视镜尾部流场状态，做XOY、XOZ和YOZ平面上的速度分布云图，如图7所示。后视镜尾部存在低速区，它们在流经后视镜表面高速气流的作用下会产生旋转方向相反的旋涡，因此后视镜尾部低速区越小，产生的旋涡越小[18]。观察XOZ平面速度分布云图可以发现：后视镜尾部存在上下两个低速区，且上方的低速区较大，向后拖拽一段距离。相比于原模型，模型1后方上下两个低速区无明显变化，而模型2后方低速区显著减小，低速中心在垂直方向上远离侧窗位置，有利于降低侧窗表面的气动噪声。观察XOY平面和YOZ平面速度云图可以看出：与原模型相比，模型2后方的低速区明显减小，而模型1无显著改善。

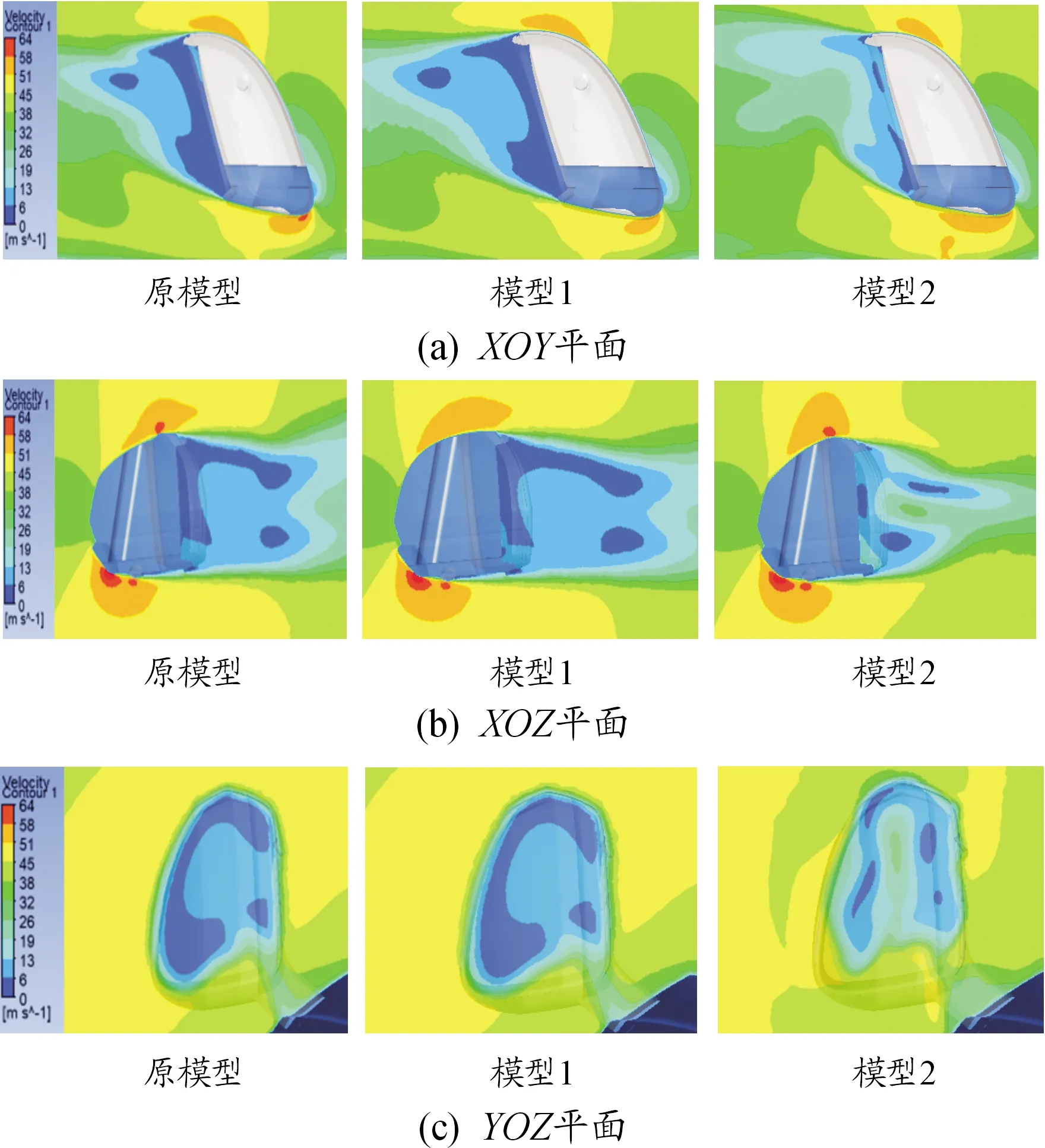
图7 3个平面上速度分布云图

通过后视镜区域的流场分析可知：不同镜壳造型对于表面气流走向具有明显影响，进而影响边界层的分离，影响后视镜尾部涡流大小。涡流在A柱-后视镜区域引起强烈的压力脉动，作用在侧窗表面形成气动噪声。通过对3种模型的对比分析发现：模型2的迎风面高于镜圈的前高后低结构引导后视镜镜壳表面气流下翻，改善了气流与镜壳表面的贴合度，防止气流向四周扩散，延缓了边界层的分离，减小了后视镜尾部涡流强度，改善了后视镜区域流场的分布。因此，可以预测模型2有利于降低侧窗表面声压级水平。

4.2 气动噪声分析

采用声比拟方法求解3种模型侧窗监测点的脉动压力，通过快速傅里叶变换(FFT)得到各监测点的声压级频谱图如图8。对比4个监测点声压级频谱图可以发现，3种模型在低频段声压级差别较小，而在中高频段差异显著，这是由于后视镜引起的气动噪声是中高频段噪声。由图7可见，除了监测点3，模型1和模型2都有一定幅度的降噪效果，这是因为监测点3距后视镜-A柱区域较远，受涡流影响较小。处于后视镜尾流区的监测点1上，模型1和模型2的降噪效果均较为显著，在中高频段1 000～5 000 Hz，取得更明显的降噪效果，其中模型2的最大降幅达到9.3 dB。在监测点2和监测点4，优化后的两种模型都取得了较好的降噪效果，模型2的降噪效果更佳，降幅最大为6.4 dB。

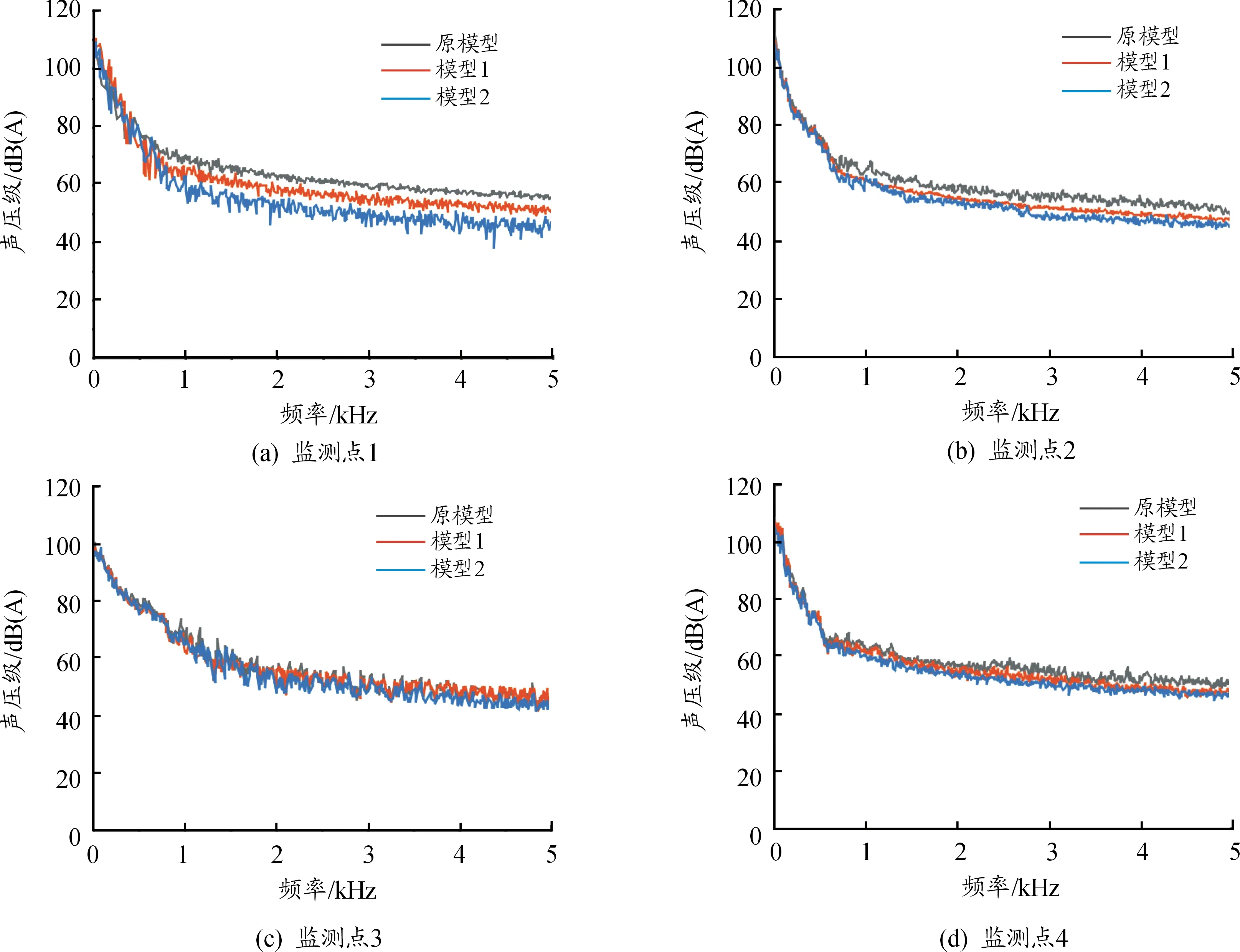
图8 声压级频谱图

综上可以推断，后视镜上方镜壳造型的优化有效地引导了表面气流的走向，使后视镜尾部湍流区域面积减小，降低了后视镜尾部湍流强度，且涡流中心远离侧窗表面，降低了侧窗表面脉动压力，改善了侧窗区域气动噪声水平，与前文流场分析结果相一致。

5 结论

1) 外后视镜镜壳造型对其尾部流场具有较大的影响，后视镜尾部涡流尺度越小，涡流中心越远离侧窗表面，越有利于降低侧窗表面气动噪声。

2) 基于某SUV后视镜模型，通过后视镜镜壳流线型造型优化，模型2尾部低速区域减小，涡流强度减小，且涡流中心远离侧窗表面，降低了对前侧窗处气动噪声的影响。

3) 后视镜引起的气动噪声表现为宽频带噪声，模型1和模型2在中高频段降噪效果较显著，模型2的声压级最大降幅达到9.3 dB，有助于改善用户的乘坐舒适性。

4) 进一步研究考虑在镜壳表面运用仿生结构，梳理后视镜表面流线，引导涡流远离侧窗位置，降低气动噪声。