智能悬架模块切换及底层控制器算法研究
赵 健,柳 江,袁 策,李明星
(青岛理工大学 机械与汽车工程学院, 山东 青岛 266520)
悬架对汽车行驶安全性和乘坐舒适性有着重要影响。传统主动悬架存在着构型相同则控制特征必然相同的桎梏,其减振效果通常只能是综合最优[1-4],而智能悬架拥有多个功能模块,可通过模块间的切换来适应不同路况,提升汽车的性能。对于汽车悬架的多模式切换策略,学者们做出了大量研究[5-7]。包黎明[8]运用模态能量法实现车辆对不同工况路面的识别,并基于神经网络算法构建悬架自适应切换策略,实现了悬架模块在不同路况下的平滑切换;汪少华等[9]提出了汽车的高度和阻尼联合控制模式,采用车身高度优先的切换策略,根据燃油经济性和汽车通过性得出模式切换参数,取得了不错的控制效果;汪若尘等[10]基于模型参考自适应控制方法研究了混合悬架多模式切换的控制,并通过仿真和实验验证了策略的有效性。但上述文献的切换策略都是悬架自适应切换策略,没有充分考虑车主的自主选择权,忽略了车主自身对车辆悬架性能的需求;此外,上述文献尽管针对不同路况进行了模块切换,但是其底层算法都采用单一算法,悬架控制优化目标的适应性受限。
因此,本文提出的智能悬架系统,充分考虑车主的自主选择权,车主可根据自己的意愿决定是否选用系统推荐的功能模块;对于本文的4个功能模块,设计了单-双阈值的模块切换策略,可实现不同路况下功能模块的分配;对于主动控制模块的底层控制器,采用不同算法进行设计,使汽车在不同路况下的性能都能得到提升。最后,本文对舒适性模块和综合性模块的底层控制器进行仿真实验,验证设计的控制器能够提升车辆性能。
1 智能悬架
1.1 智能悬架结构
智能悬架结构如图1所示,由传感器、模数转换器、数模转换器、弹簧、减振器、直流电机、储能装置和ECU组成。

1.车身; 2/11.传感器; 3/12.模数转换器;4.弹簧; 5.减振器; 6.直流电机; 7.数模转换器; 8.ECU; 9.储能装置; 10.轮胎;13.地面
1.2 智能悬架功能模块
智能悬架功能模块如图2所示,馈能模块可用来储存车辆悬架振动产生的能量,尤其适合电动车辆的增程;而主动控制模块则用来改善汽车平顺性和行车安全性,提升汽车性能。

图2 智能悬架功能模块框图
悬架功能模块的简单介绍如下所示:
1) 馈能模块
电机将悬架振动产生的能量转化为电能,并储存在储能装置中。车主可在良好路面行驶时选用,适用于车辆的连续行驶;也可在综合性模块时选用馈能模块,继续回收电能。
2) 舒适性模块
采用误差反向传播(back propagation,BP)神经网络控制和PID控制(PID control)算法相结合的BP-PID控制算法,以车身加速度为优化对象,提升汽车平顺性。
3) 安全性模块
采用模糊控制(fuzzy control,FC)算法,以轮胎动位移为优化对象,提高轮胎的抓地能力,增强行车安全性。
4) 综合性模块
采用线性最优(linear quadratic gaussian,LQG)算法改善汽车平顺性和行车安全性,提高车辆的综合性能。
1.3 智能悬架工作框架
车辆行驶路况变化时,用户对悬架性能的需求亦会变化,智能悬架能为车主推荐合适的功能模块,满足车主的性能需求。
智能悬架工作过程如图3所示,主要包含软硬件两部分,软件由悬架的上层模块切换算法、功能模块、下层控制算法以及车载APP组成;硬件包括ECU、悬架控制器、直流电机和储能装置,其中ECU对应上层算法,悬架控制器对应下层算法。当车辆行驶路况发生变化时,ECU对传感器传输的振动信号进行判断处理,通过车载APP将相应的功能模块推荐给车主,车主便可自主决定是否选择该模块,当车主确认选择后,悬架控制器会控制电机进入相应的工作状态:当车主选择主动控制模块时,电机以纯电动机状态工作,在相应算法的控制下,输出合适的主动力,提升悬架的性能;当选择的功能模块为馈能模块时,电机以纯发电机状态工作,回收的电能通过控制电路传输给储能装置,为其他用电设备提供电能;当车主既选择主动控制模块又选择馈能模块时,电机以可馈能的电动机状态工作,在输出控制力的同时,进行馈能。需要指出的是,考虑到行车安全,车载APP采用语音提示切换类型,用户通过语音识别或视屏确认,相关技术和产品比较成熟,不再赘述。

图3 智能悬架工作过程框图
2 模块切换控制策略
根据A级至D级4种路面切换功能模块,D级以下路面归于D级。
2.1 单-双阈值的顺序判定切换规则
轮胎动位移直观地体现了轮胎抓地力的大小,是行车安全性的评价指标;车身加速度直观地体现了用户的乘坐舒适性,是汽车平顺性的评价指标。因此,以这2个评价指标作为模块切换的评价标准,并设定相应的阈值。
通常而言,汽车安全性比舒适性更加重要。所以,本文提出一种具有判定顺序的单-双阈值切换规则[11],以轮胎动位移为第一级判断标准,车身加速度为第二级判断标准,结论为路面类型(road mode,RM)。这种顺序判定规则,明确了安全性优先的准则,判别计算效率也有所提升。
制定悬架功能模块的判定方法如下所示:

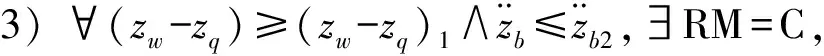

由上述分析,制定出功能模块切换规则,如表1所示。

表1 功能模块切换规则
2.2 功能模块阈值的设定
通过仿真得知,轮胎动位移和车身加速度这2个评价指标都与车速、路面不平度成正相关。通常而言,汽车行驶时,车速基本稳定在10~30 m/s (36~108 km/h)。此时,汽车在A级路面上行驶时,2个指标值都较小;在D级路面上行驶时,2个评价指标都较大;而汽车在B级或C级路面上行驶时,车速不同可能出现2个指标值接近的情况。因此,阈值设定的关键在于能够准确区分B级与C级路面。

(zw-zq)1=(zw-zq)Bmax
(1)
(2)
(3)

2.3 功能模块切换控制流程
功能模块切换控制流程如图4所示,当车辆行驶路况变化时,车轮和车身上的传感器将信号传输给ECU,ECU对信号进行判断处理,计算出轮胎动位移和车身加速度实际的均方根值,并与设定的阈值相比较,确定相应的功能模块,通过车载APP将其推荐给车主,车主确认选择该模块后,将这一信息传输给悬架控制器,控制悬架进行模块切换。

图4 功能模块切换控制流程框图
3 底层控制器设计及仿真分析
对所有功能模块进行仿真实验,由于汽车经常行驶的路面为B级和D级路面,因此仅列举舒适性与综合性控制器这2个底层控制器,控制+馈能的算法可参看文献[12-13]。
3.1 路面模型的建立
以滤波白噪声生成随机路面输入模型,即:

(4)
式中:zq为路面位移(m);f0为下截止频率(Hz);G0为路面不平度系数(m3·cycle-1);u0为车辆前进速度(m/s);w为数学期望为0的高斯白噪声。
3.2 车辆系统动力学模型
3.2.12自由度1/4车辆模型的建立
建立2自由度1/4车辆模型如图5所示。
图5中,mb为车身质量(kg);mw为车轮质量(kg);ks为悬架刚度(N ·m-1);kt为轮胎刚度(N ·m-1);f为悬架主动控制力(N);cs为悬架阻尼系数(N·s·m-1);zb为车身位移(m);zw为车轮位移(m);zq为路面位移(m)。

图5 2自由度1/4车辆模型示意图
可得车辆模型的动力学方程为:

(5)
(6)
3.2.2系统状态方程
对于1/4车辆模型而言,车身加速度、轮胎动位移和悬架动行程是车辆悬架主要的性能指标。因此,选取系统的状态变量X和输出变量Y为:
(7)
则系统的状态空间方程为:

(8)
式中:

其中,A为系统矩阵;B为控制矩阵;C为输出矩阵;D为传递矩阵;H为路面输入矩阵;控制力输入矩阵U=f;高斯白噪声输入矩阵W=w。
3.3 车辆模型仿真参数
以某轿车为研究对象[14],车辆模型的有关参数如表2所示。

表2 车辆模型仿真输入参数
3.4 舒适性控制器的设计与仿真
PID控制器结构简单易调节,但控制器参数间存在非线性和时变性等问题,不能保证稳定控制;而BP神经网络能充分逼近非线性函数,可以弥补PID控制器的缺陷。因此,将这2种算法结合,提出一种复合型算法——BP-PID控制算法[15-17]。对于悬架的舒适性模块,以车身加速度为优化目标,采用BP-PID控制改善汽车平顺性。
3.4.1舒适性控制器的设计
BP-PID控制器结构如图6所示,由BP神经网络和PID控制器组成。图6中,r为系统的期望输出值,y为实际输出值,e为两者间的偏差;kp、ki和kd分别是比例系数、积分系数和微分系数;u为输出控制力。BP神经网络实时整定PID控制器的3个参数,然后PID控制器通过控制力u对1/4车辆模型进行闭环控制,使系统获得最佳性能指标。

图6 BP-PID控制器结构示意图
BP神经网络结构如图7所示。BP神经网络采用3层网络结构,输入层神经元个数为4,分别为x1=r(k),x2=y(k),x3=e(k),x4=1。r(k)、y(k)分别为系统第k次的期望输出值和实际输出值,e(k)为两者间的偏差;输出层神经元的输出值为PID控制器的参数kp、ki和kd,所以输出层节点数取3;隐含层节点数过多则计算量增大,过少会导致BP算法的函数逼近效果变差,综合考虑隐含层神经元个数定为5。综上,确定BP神经网络的结构为4-5-3。

图7 BP神经网络结构示意图
网络输入层神经元的输入为xj,其输出为:

(9)
网络隐含层神经元第k次的输入、输出为:
(10)
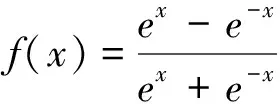
(11)
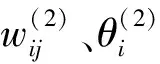
网络输出层神经元第k次的输入、输出为:
(12)
其中,
(13)
(14)

取性能指标函数如下所示:

(15)
采用带有惯性项的梯度下降法对BP网络的权值进行修正,使E(k)快速收敛于对权值的负梯度方向。
(16)
(17)

(18)

利用符号函数sgn[∂y(k)/∂u(k)]近似代替未知量∂y(k)/∂u(k),造成的计算不精确通过调整η来补偿。可得网络输出层权值和阈值的修正公式:
(19)

同理,网络隐含层权值和阈值的修正公式为:
(20)

3.4.2舒适性控制器的仿真与分析
由上述分析计算,在Matlab/simulink中建立仿真模型,选择B级路面作为道路输入,得智能悬架和被动悬架各性能指标的对比如图8~10所示。

图8 车身加速度曲线

图9 悬架动行程曲线

图10 轮胎动位移曲线
由图8~10可得,相较于被动悬架,采用BP-PID算法的舒适性控制器非常明显地降低了车身加速度(body acceleration,BA),即改善了汽车平顺性;但是悬架动行程(suspension working space,SWS)和轮胎动位移(dynamic tire displacement,DTD)的峰值均有一定程度的增大,即表现为轮胎抓地力变弱。为了定量化分析悬架各性能指标的变化情况,作出悬架3个性能指标的均方根值(RMS),如表3所示。

表3 仿真结果均方根值
由表3可得,在采用BP-PID算法的舒适性控制器作用下,智能悬架的BA减小了46.15%,汽车乘坐舒适性明显提升;SWS增大了21.74%,在符合设计要求(±100 mm)的前提下,有利于馈能;但DTD增大了43.48%,尽管在DTD整体较小的情况下,可以认为舒适性控制器的设计满足悬架系统要求,但仍须重视汽车乘员的安全性问题。因此,这种算法只适用于舒适性模块,不适用于路面状况较差、轮胎垂向振动较大的安全性和综合性模块。
3.5 综合性控制器的设计与仿真
对于综合性模块,以车身加速度、悬架动行程和轮胎动位移共同作为优化目标,采用LQG算法改善汽车平顺性和行车安全性。
3.5.1综合性控制器的设计
综合性控制器的性能指标函数J即为上述3个评价指标加权平方和在时域T内的积分。其表达式为:
(21)
式中:q1、q2和q3分别是各性能指标的加权系数。
加权系数的选取决定了评价指标的重要程度,本文经过多次测试,确定合适的权值系数q1=1,q2=500,q3=20 000,使其既能满足汽车的平顺性要求,又能提供良好的行车安全性。
根据最优控制理论,将式(21)改写成如下形式,即:
(22)
式中:Q、R分别是状态变量、控制变量的加权矩阵;N为交叉项的权重。
由Matlab软件中的lqr函数,求出最优增益反馈矩阵K,即:
[K,S,E]=lqr(A,B,Q,R,N)
(23)
式中:S为Riccati方程解;E为系统特征值。
根据反馈状态变量X(t),可得出作动器在时刻t的最优控制力U(t):
U(t)=-KX(t)
(24)
3.5.2综合性控制器的仿真与分析
由上述分析计算,在Matlab/simulink中建立仿真模型,选择D级路面作为道路输入,得智能悬架和被动悬架各性能指标的对比,如图11~13所示,RMS如表4所列。

图11 车身加速度曲线
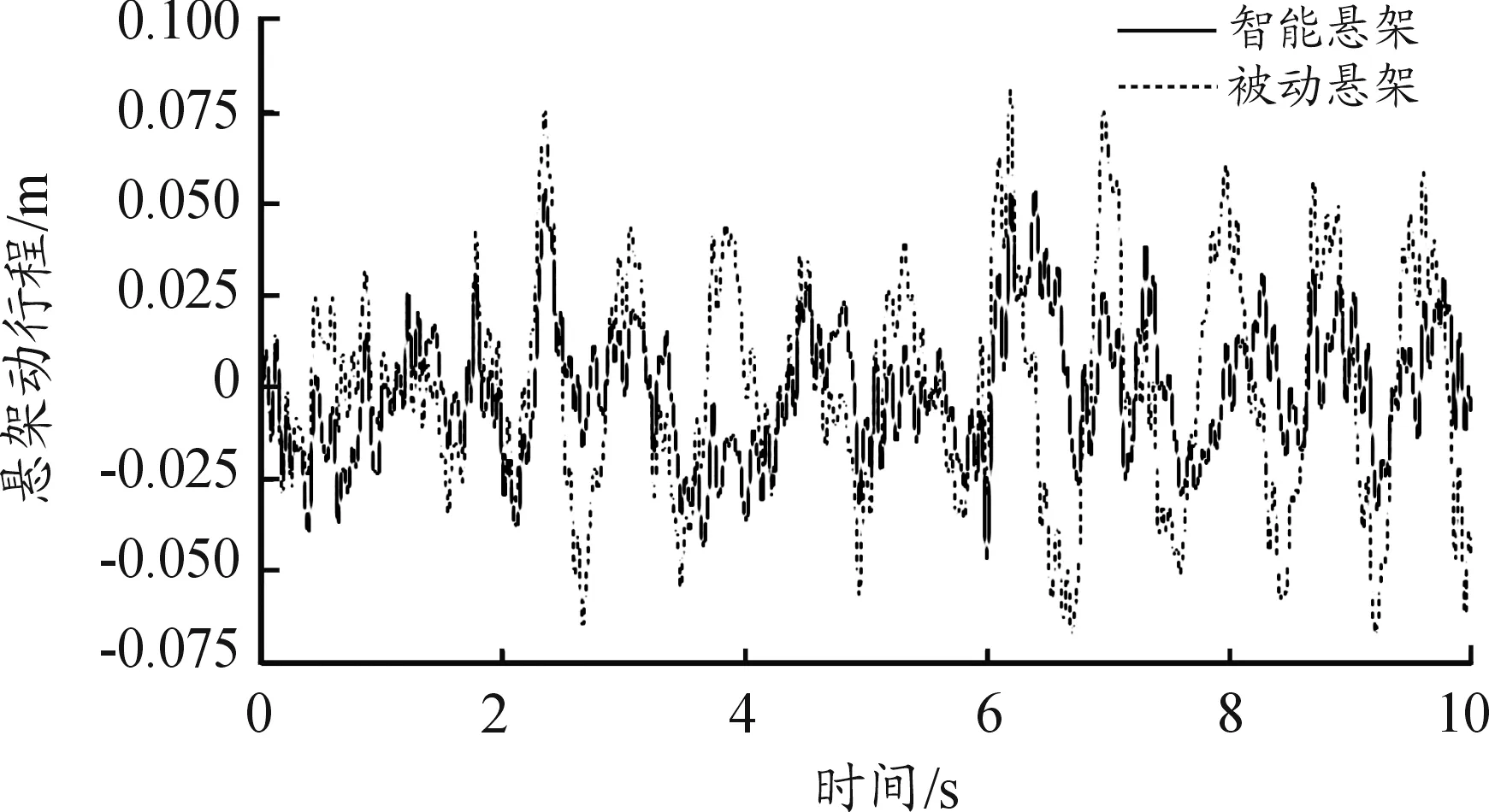
图12 悬架动行程曲线

图13 轮胎动位移曲线
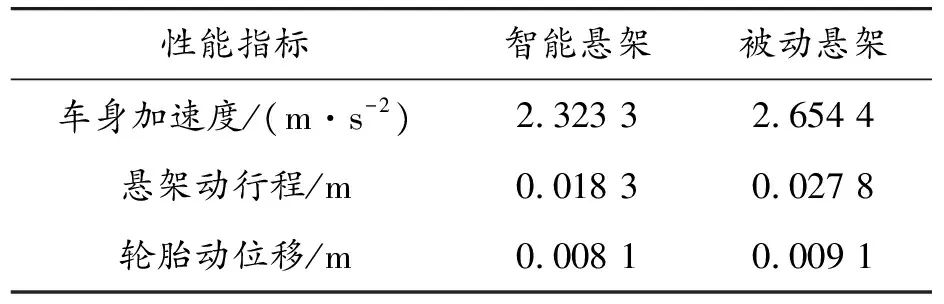
表4 仿真结果均方根值(RMS)
分析上述图表可得:相较于被动悬架,在采用LQG算法的综合性控制器作用下, BA、SWS和DTD分别降低了12.47%、34.17%、10.99%。悬架3个评价指标中,智能悬架的SWS改善最大,有效降低了悬架击穿概率,使悬架工作空间得到更充分地利用;BA和DTD的降幅也超过10%,即汽车平顺性和行车安全性得到提升,综合性控制器的设计满足要求。
4 结论
1) 在双层结构智能悬架基础上引入用户决策环节,更好地满足了路况变化时车主对悬架性能需求的差异;设计了单-双阈值的顺序判别规则,明确了安全性优先的切换策略。
2) 以舒适性控制器和综合性控制器为例,进行仿真实验,结果表明:智能悬架在B级路面能够改善乘坐舒适性(BA减少了46%),在D级路面能够提升汽车悬架性能,其中BA改善了12.47%,SWS减小了34.17%,DTD降低了10.99%。

