基于锁相环改进SVPWM同步调制技术的研究
单宝钰,尹国龙,高宏洋,刘金晶
(中国中车大连电力牵引研发中心有限公司,大连 116022)
0 引 言
永磁同步电机(以下简称PMSM)转子结构由永磁体替代了异步电机的励磁绕组的结构,降低了高速运行时转子发热的问题,并且PMSM具有体积小、效率高、低速转矩大等优势,渐渐地被应用在需要高速运行、负载变化大的领域。由于PMSM相比异步电机极数多,当大功率运行时,受功率开关器件温升限制,需要降低开关频率,因此高速区运行采用波形对称的SVPWM同步调制控制策略。但是,传统SVPWM同步调制策略随着载波比减小,输出谐波含量高,无法平滑切换到方波运行,逆变器开关损耗大,导致逆变器发热严重。
文献[1]介绍了多模式SVPWM同步调制原理和采样方式,与传统SVPWM异步调制进行了比较,验证了方法的合理性和可行性,但该方法调制波为传统SVPWM调制波形,全速度范围运行时存在模式间切换,且最终只能切换到9分频运行,实际PWM脉冲数为9,谐波含量高,逆变器开关损耗大。
文献[2]采用了多模式调制方法,即SVPWM异步调制—SVPWM同步调制—特定谐波消除PWM—方波调制,实验验证了方法的可行性。虽然文中简化了数学模型和切换方式,但还是存在多模式之间切换时的波形不连续问题,实验采用电机功率较小,切换过流等问题并未体现,在实际工程应用中电机功率较大,外部供电因素干扰使切换过流问题更加明显。
文献[3]采用方法虽也为同步调制方式,但存在多模式转换,无法实时调节,实际工程化应用时存在动态响应不高,容易引起切换过流的问题。
针对以上问题,本文提出了一种基于锁相环改进SVPWM同步调制算法,通过在高速区引入简化单模式连续过调制算法,实现高速区平滑切换至方波,减小输出谐波含量,减小开关次数,降低开关损耗。由于简化单模式连续过调制方式无需计算开关角及区分模式转换,简化了数学模型和计算过程,减少了程序计算量,提高了算法执行效率[4]。
1 基于锁相环SVPWM同步调制
1.1 SVPWM同步调制基本原理
SVPWM同步调制算法是在异步调制基础上,结合同步调制对称的特点进行了优化,在变频调速控制时始终保持载波和调制波同步变化,使得PWM脉冲输出半波奇对称、四分之一周期偶对称和三相对称[5]。
相比SVPWM异步调制算法间隔恒定的采样方式,SVPWM同步调制算法则采用空间电压矢量相位差恒定的采样方式。通过使空间电压矢量相位三相对称、电压波形正负半周对称、电压波形在最大值或最小值的轴线对称,即每个扇区采样的次数为奇数、采样矢量关于每个扇区的角平分线对称,原理如图1所示[6-7]。

图1 同步采样原理示意图
异步电机空间电压矢量相位采用开环控制,但PMSM矢量控制时需要定转子相位绝对保持一致,因此对空间电压矢量相位进行闭环控制,通过等幅值的坐标变换转换到指定的对称角度,原理框图如图2所示。

图2 同步采样补偿原理框图
以第一扇区为例,根据伏秒平衡原则可知,空间电压矢量数学模型如下:
(1)
式中:t0为零矢量作用时间;t1为空间电压矢量作用时间1;t2空间电压矢量作用时间2;Ts为开关周期;α为空间电压矢量相位角[8-9]。
1.2 基于锁相环同步调制策略
PMSM相比于异步电机极对数多,在同样的转速范围内,PMSM的最高频率比异步电机高,并且由于其定、转子频率需要严格保持一致,不能出现失步现象,因此其在高速下的脉冲调制方式与异步电机不尽相同。
无论异步电机还是PMSM,当载波比小于15时,为保证线电压最大限度的对称,一般都需要使用同步调制策略,使调制波和载波比保持一致。
本文使用锁相环把电压相位与载波相位锁定,即当线电压相位变化时,通过锁相环函数PI调节器调节载波周期,使载波以同样的趋势改变相位,最终达到两者相位角度实时保持一致。载波计数周期和PWM中断频率关系:
(2)
式中:fPWM为PWM中断频率;fsw为开关频率。
锁相环的具体实现方式为在每一个中断函数中,计算合成空间电压矢量Us与α轴的夹角θ,并把该角度作为反馈值,送入锁相环调节模块,用于载波周期值的调整。Us的起始角度可以任意取值,这里Us的起始角度为α轴位置。
锁相环输出量用于调节载波周期的大小,即:
(3)

基于锁相环的同步调制流程图如图3所示。

图3 软件执行流程图
以9分频为例,根据同步调制采样规则可得算法的调制波和载波波形如图4所示。

图4 SVPWM同步算法波形
以上基于锁相环SVPWM同步调制算法在PMSM矢量控制策略中最后过渡到9分频,需要进行调制切换到方波调制状态,为了进一步降低开关频率,减小逆变器损耗,提高母线电压利用率,本文通过引入简化单模式过调制算法,在此基础上,使逆变器平滑过渡到方波工作状态[10-11]。
1.3 简化单模式过调制数学模型
传统大功率永磁电机牵引控制采用SVPWM异步调制—SVPWM同步调制—方波调制,存在多模式切换,模式之间过渡不平滑,且无法直接过渡到方波运行,运算复杂。本文通过引入简化单模式过调制算法,简化了过调制区切换和扇区判断,减小了算法运算量,提高了算法执行效率。
根据矢量控制算法电压计算数学模型可得:
(4)


图5 空间电压矢量扇区关系
以第一扇区为例,由式(1)可得:
(5)
根据三相电压相位关系可得空间电压矢量作用时间[6-7]:
(6)
式中:t0为零矢量作用时间;t1为空间电压矢量作用时间1;t2空间电压矢量作用时间2;Ts为开关周期。
(7)
(8)
式中:um为中间简化算法中间计算变量;t′1,t′2为过调制区空间电压矢量作用时间;Ta,Tb,Tc分别为三相调制波比较值。
2 改进SVPWM同步调制算法仿真分析
2.1 仿真模型
通过前文数学模型推导,搭建基于锁相环改进SVPWM同步调制仿真模型,进行算法验证和谐波含量分析。
如图6所示,仿真模型包含PMSM、矢量控制算法模型、SVPWM同步过调制算法模型、逆变器电路和检测电路。

图6 改进SVPWM同步调制PMSM控制系统
仿真参数如下:
Time0采样时间为10 μs,Time1采样时间为1 ms,网压Uline= 800 V,仿真用电机参数与实验用电机参数保持一致:Un= 530 V,Pn= 106 kW,fn= 68 Hz,Rs= 0.015 35 Ω,Ld= 0.000 749 1 H,Lq= 0.001 277 5 H,Fm= 0.274 Wb,8极。

图7 改进SVPWM同步调制作用时间仿真模型
SVPWM同步过调制作用时间仿真模型包含了同步过调制算法和传统同步调制算法模型,通过模式选择进行切换。
2.2 分频波形对比分析
如图8所示,以9分频为例,当给定调制系数为0.9时,传统SVPWM同步调制实际脉冲数为9,此时同步过调制算法未进入过调制区,实际脉冲数也为9。
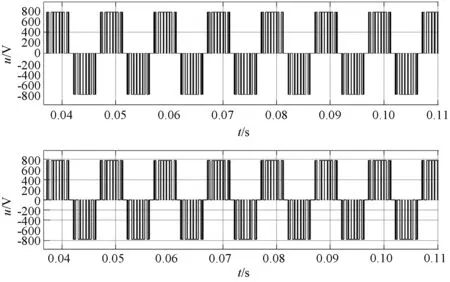
图8 SVPWM同步调制和同步过调制波形1(调制系数0.9)
如图9所示,上半部分为同步过调制算法,下半部分为传统同步调制算法。进一步给定调制系数为1.0时,由于调制系数超过0.906 9时,进入过调制区。传统同步调制给定为0.9,两种算法实际脉冲数为9和6。

图9 SVPWM同步调制和同步过调制波形2(调制系数1.0)
如图10所示,上半部分为同步过调制算法,下半部分为传统同步调制算法。当调制系数为1.1时,SVPWM同步过调制算法实际脉冲数为3。

图10 SVPWM同步调制和同步过调制波形3(调制系数1.1)
如图11所示,上半部分为同步过调制算法,下半部分为传统同步调制算法。当调制系数为1.2时,SVPWM同步过调制算法实际脉冲数为1。

图11 SVPWM同步调制和同步过调制波形4(调制系数1.2)
通过线电压输出对比可知,相比传统算法,逆变器开关次数降低了66%以上,大幅降低了逆变器开关损耗。当调制系数由1.1调整为1.2时,同步过调制算法下,调制波波形由三脉冲顺利过渡到单脉冲的方波模式,进一步降低了开关频率和开关损耗。
SVPWM同步过调制可平滑过渡至方波运行,且波形连续平滑,下面针对两种算法输出谐波含量进行对比分析。
2.3 谐波对比分析
当电机运行在1 500 r/min(100 Hz)和3 000 r/min(200 Hz)时,进行传统算法和改进算法谐波对比分析,结果如图12~图15所示。

图12 传统算法Ia及其谐波含量波形图(1 500 r/min)

图13 改进算法Ia及其谐波含量波形图(1 500 r/min)

图14 传统算法Ia及其谐波含量波形图(3 000 r/min)

图15 改进算法Ia及其谐波含量波形图(3 000 r/min)
通过谐波含量对比分析可以看出,SVPWM同步过调制算法有效降低了5次和7次谐波,整体谐波含量相比传统算法降低了2%以上。
3 改进SVPWM同步调制算法实验
实验设备采用100%低地板永磁牵引系统实验平台。直流供电电压800 V,PMSM极数8极,额定功率106 kW,DL850示波器。

图16 永磁牵引系统实验柜体
以太网与牵引控制单元进行通信,观测本文方法三脉冲和方波运行时的稳定性以及过渡切换时电流畸变情况,可验证本方法的可行性。实验波形如图17、图18所示。

图17 SVPWM同步过调制多脉冲过渡到三脉冲

图18 SVPWM同步过调制三脉冲过渡到方波
SVPWM同步过调制调制波连续,因此不存在多模式切换下的相位畸变,未产生电流冲击,甚至过流保护情况。实验验证了本方法可实现平滑过渡到方波运行。
4 结 语
本文提出了一种PMSM SVPWM同步过调制算法,建立了数学模型和仿真模型,并且对算法进行了简化处理,取消了过调制区计算和扇区判断,通过检测三相电流直接计算出空间电压矢量作用时间,实现了异步调制和过调制运算的连续性,提高了算法运算效率。
相比传统SVPWM同步调制算法,本方法有效降低了输出谐波含量,降低了开关频率,减小了逆变器发热,提高了系统效率,减少了能耗损失。
通过仿真实验,对比分析了输出波形和谐波含量;进行了地面联调实验,实验结果得出输出电压可以平滑过渡到方波运行,过渡过程没有明显冲击和振荡,从而验证了本方法的合理性和可行性。

