一种磁悬浮球形感应电机的仿真特性分析

严博丰，徐衍亮，吴春九，焉来军，黄志斌

(1.中国电力科学院 电力工业电气设备质量检验测试中心，武汉 430074；2.山东大学 电气工程学院，济南 250100)

0 引 言

相较于传统电机，磁悬浮球形电机的转子是一个磁悬浮球体，可以在三维空间任意方向持续旋转，从而输出任意方向的姿态控制力矩，避免了多个传统飞轮之间固有的动力学耦合问题，控制精度和驱动效率更高。磁悬浮球形感应电机作为一种特殊用途的电机，在工作过程中不仅要能够提供3个自由度上的旋转转矩，还需要同时兼顾磁悬浮轴承的悬浮力输出。

本文给出了一种浮转一体的磁悬浮球形感应电机，该电机没有专门的磁悬浮支承部件，而是利用旋转驱动磁极，在产生旋转驱动的同时，产生悬浮驱动，从而有效降低了电机结构的复杂性，提高了电机的功率密度和转矩密度。

1 浮转一体磁悬浮球形感应电机的结构及基本原理

浮转一体磁悬浮球形感应电机由定子和球转子组成，其原理结构图如图1所示。导磁球壳外表覆铜构成了球电机的转子，在定子上，以过转子球心的X、Y、Z坐标轴为对称轴，对称分布了6个完全相同的定子块X1、X2和Y1、Y2及Z1、Z2，各定子块由完全相同的铁心块和其内周的三相对称绕组构成。相对称的两个定子块中，三相对称电流的有效值分别为I0+ΔI和I0-ΔI，其中I0为偏置电流，ΔI为控制电流。这两个定子块中的三相对称电流会在定转子气隙中产生沿其对称轴旋转的磁动势和磁场，旋转磁场在转子表面覆铜中产生感应电动势和感应电流，感应电流与旋转磁场相互作用而受力，从而使球电机沿两定子块对称轴旋转；同时两定子块中的偏置电流I0产生的旋转磁场当作偏置磁场，两定子块中的控制电流产生的旋转磁场当作控制磁场，从而使球转子在两磁极块所在平面方向上悬浮。

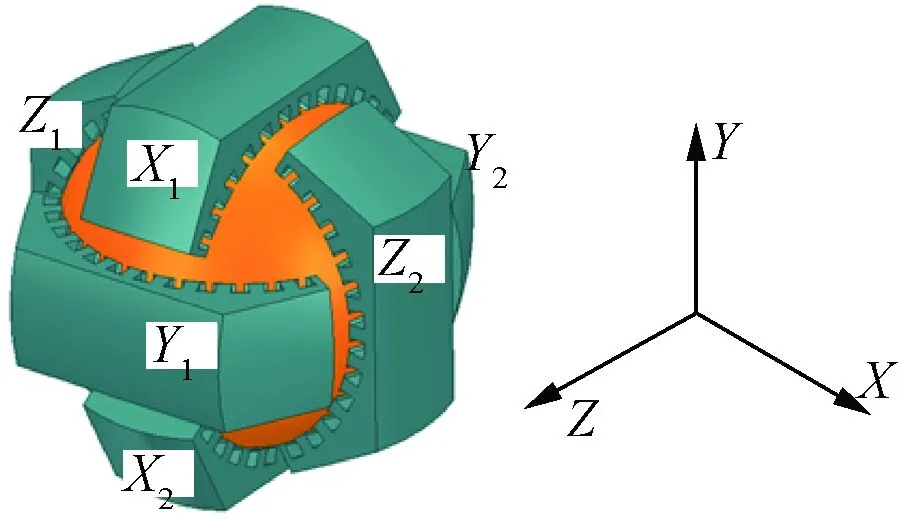
图1 浮转一体磁悬浮球形感应电机的原理结构图

值得注意的是，每个定子磁极为2极、占有120°机械角度，换算成360°机械角度的整圆电机，则电机为6极，因此电机同步速ns与电流频率f之间满足：f=3ns/60。

电机的旋转额定运行状态为2 000 r/min、15 mN·m[1]，并具有低额定运行输入功率。上述球转子的悬浮力为12 N，因此考虑球转子的悬浮支承，悬浮力应高于球转子的1.5倍，即高于18 N。

2 感应电机电流源驱动的电磁转矩-转差率分析

对电流源驱动的感应电机来说，相同的额定工作点，可以有不同的定子电流、定子频率(即转差率)组合(Is，f)，由此具有不同的损耗等其他电机性能。

电流源供电的感应电机T型等效电路如图2所示。图2中，R1及R′2分别为电机定子绕组电阻和转子绕组电阻折算值;L1σ及L′2σ分别为电机定子绕组漏电感和转子绕组漏电感的折算值；Lm为激磁电感;s为转差率，I1、I′2及Im分别为定子电流(等于电源电流Is)、转子电流折算值及激磁电流。

图2 电流源供电的感应电机T型等效电路

从图2的等效电路可以较容易得到电机的电磁转矩表达式：

(1)

由此得到感应电机在电流源供电时的电磁转矩-转差率曲线，如图3所示。在忽略电机的激磁电流时，电机转子绕组电流折算值与电机定子绕组电流相等，即为电流源输出电流Is。

对Te求导，得到临界转差率sm：

(2)

将式(2)代入式(1)便得到最大转矩：

(3)

由式(2)、式(3)可以看出，在电流源供电时，感应电机的临界转差率sm与转子电阻折算值成正比、与电源频率f成反比；最大转矩Tem与转子电阻无关，这一点与电压源供电感应电机具有相同的特点。同时，电机的稳态工作点位于低于临界转差率sm的某个点上，如图3中的(sN，TN)，而且最大转矩Tem与额定转矩TN的比值为过载倍数kM，显然，过载倍数也是感应电机的重要性能指标。

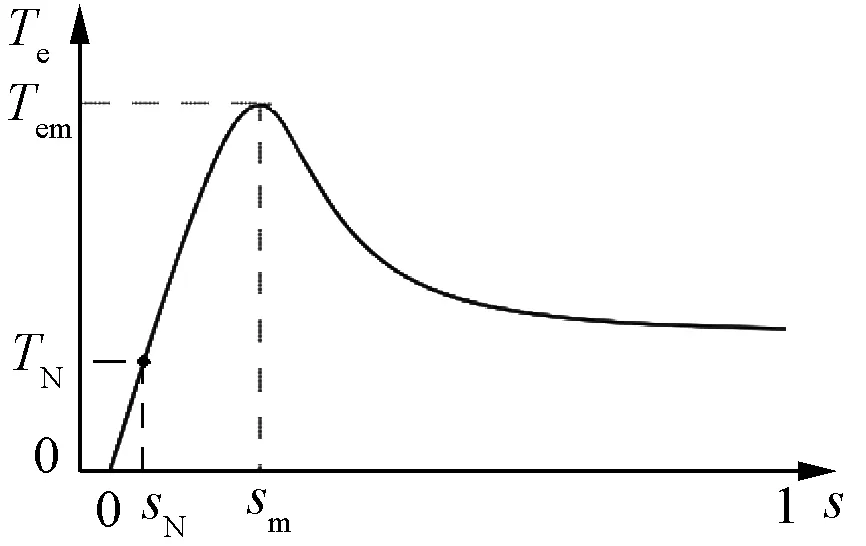
图3 电流源供电的感应电机转矩转差率特性曲线

电流源电流Is保持不变，感应电机的Te-s曲线随电源频率f的变化曲线如图4所示。频率f保持不变，Te-s曲线随电源电流Is的变化曲线如图5所示。由图4和图5可以看出，对已制作完成的电流源驱动感应电机来说，其额定工作点有多个电源电流Is及频率f组合，即其额定工作点可以通过不同的电流Is和频率f实现，但是不同的Is和f具有不同的功率因数、功耗、运行效率及过载倍数。

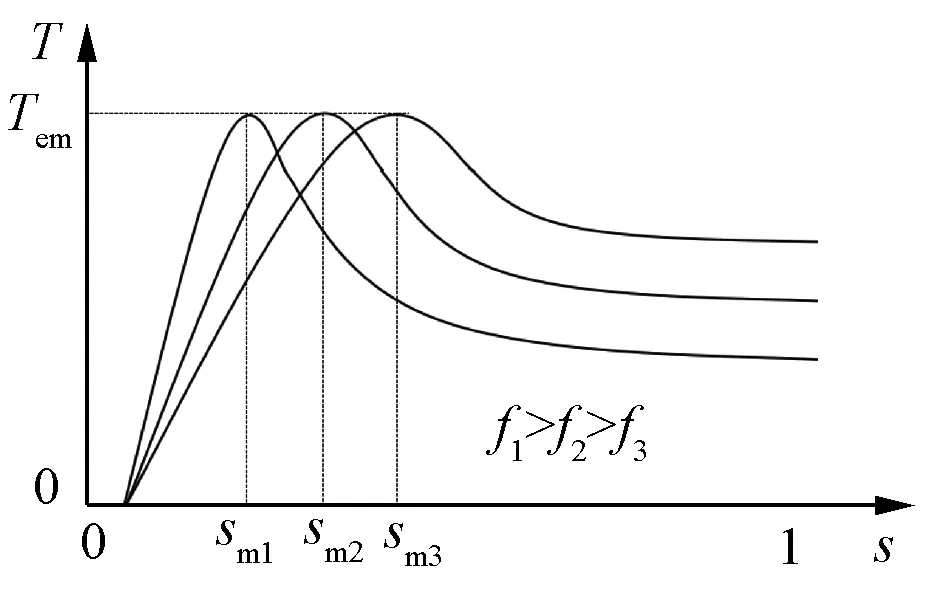
图4 不同频率下感应电机的转矩转差率特性曲线

图5 不同电源电流时感应电机转矩转差率特性曲线

例如，仅从损耗的角度，为保证额定工作点不变，增大电流频率(导致电机的转差率增大)时必须降低电源电流大小，电流变化使定转子铜耗、定转子铁耗都有变化，从而影响总损耗和电机发热、温升。

考虑到本文分析的浮转一体式球形感应电机的额定性能要求，即电机必须满足稳定运行转速2 000 r/min，输出转矩大于等于15 mN·m的额定要求，因此接下来的分析与仿真计算均考虑电机保持2 000 r/min，15 mN·m的情况，对电机施加不同驱动电流、频率的组合也应满足这一条件。

3 浮转一体球形感应电机额定工作时的(Is， f)组合性能研究

3.1 浮转一体球形电机仿真模型建立

浮转一体磁悬浮球形感应电机是三维磁路结构电机，在进行仿真研究时需要采用3D电磁场有限元方法(3D-FEM)，但是3D-FEM计算特别是瞬态场计算，带外电路的瞬态场计算需要很高的计算资源和很长的计算时间。实际上，尽管电机是三维球形结构，但是与一般旋转电机的运行原理没有区别，完全可以采用二维有限元方法进行分析，只不过在仿真分析时，铁心厚度不是实际的铁心叠片厚度，而是定子块内周沿旋转轴方向的弧长长度。

图6及图7分别为浮转一体球形电机的单自由度旋转仿真时的等效二维场仿真模型图及剖分图。赋值电机各构成材料的属性、边界条件，然后施加不同频率、不同电流有效值的三相对称电流源激励，可以进行电机的电磁场有限元仿真计算，得到相关性能参数及损耗参数。

图6 浮转一体球形感应电机单自由度旋转时二维场仿真模型

图7 浮转一体球形感应电机二维场仿真剖分图

3.2 额定工况下(Is，f)组合分析

基于上述有限元模型，满足额定工况下得到不同的(Is，f)组合，如表1所示。其中，对不同组合给出过载倍数、总损耗，图8给出了不同组合时的磁密分布。

表1 浮转一体球形感应电机各(Is， f)组合分析结果

图8 不同(Is，f)组合下电机的各部分磁密

由表1及图8可以看出：

(1)如前所述，不同的(Is，f)组合可产生相同的额定工作状态(2 000 r/min，15 mN·m)，但不同组合具有不同的损耗。在每一状态的损耗中，转子铜耗、定子绕组铜耗、定子铁耗及转子铁耗依次降低，其中定转子铁耗特别是转子铁耗很低，可以忽略不计，因此降低转子铜耗是降低整体功耗的关键。

(2)随着频率的增加，满足额定工作要求的定子绕组电流降低，形感应球电机的总损耗降低，构成总损耗的各部分损耗都降低。可见，提高频率，有利于降低电流、降低电机的总损耗，但是太小的定子绕组电流不能满足电机的悬浮要求，因此，在满足悬浮要求的前提下需要采用尽可能高的频率，从而降低电机电流，降低电机的总损耗。

(3)表1中，电源频率最低为160 Hz，对应的电机同步速为3 200 r/min，此时电机的转差率为0.375，完全不同于普通感应电机具有较低转差率的运行状态。实际上，尽管转差率较大，但电机定转子铁耗较低。

(4)由图8可以看出，各个(Is，f)下的电机运行磁路都没有饱和，这也是定转子铁耗较低的主要原因。

(5)频率增大，电机的过载倍数降低，对电机的旋转稳定性不利。

由表1可以看出，电源频率最低为160 Hz，再降低电机频率，即使绕组电流大，也不能满足额定运行要求，原因是电流的增大导致总损耗增大。同时，电机的端部效应导致电机的出力降低，从而使电机不能运行于额定状态，下面具体分析端部效应对电机的影响。

3.3 端部效应对电机性能的影响

如前所述，电机一个自由度运行时只有相对称的分别占有120°机械角度的两个完全相同的磁极铁心构成。由表1所示，电流的最低频率为160 Hz左右，再降低电流的频率无法满足电机的额定输出，其主要是定子铁心断开而导致的端部效应。两端开断，三相对称电流通入到三相绕组中产生的磁场分布如图9所示。显然，在初级两端开断处的磁通分布与中间铁心部分的磁场分布完全不同，不但磁场较弱，而且发生了严重畸变，这就是所谓的端部效应。由于铁心和槽中绕组在两端处不连续，所以各相之间的互感不相等，当三相绕组通入对称的三相交流电流时，产生的三相反电动势也不对称，这就产生了正向正序行波磁场、反向负序行波磁场和零序脉振磁场，后两类磁场在电机次级运行过程中会产生额外的阻力和附加损耗。同时，初级开断产生相对初级不移动的脉振磁场，可导致电机运行过程中的推力波动，这也是直线电机发生推力波动的主要因素。

图9 一角铁三相绕组通入三相对称电流产生的磁场分布

在对球形感应电机进行120 Hz、1.5 A组合时的仿真计算时，将该电机组合成整圆电机，如图10所示，电机每线圈匝数调整为原电机的2/3，其他完全相同。原电机相对的两个磁极铁心通入三相对称电流时产生相同方向的旋转磁场，整圆电机相当于3个完全相同的角铁，通入三相对称电流时也产生相同方向的旋转磁场。可以看出，这一比较是在相同输入电流源(频率和电流)、相同总安匝磁动势、相同定子相电阻、相同定子铜耗下进行，差异是前者具有端部效应，而整圆电机没有端部效应。

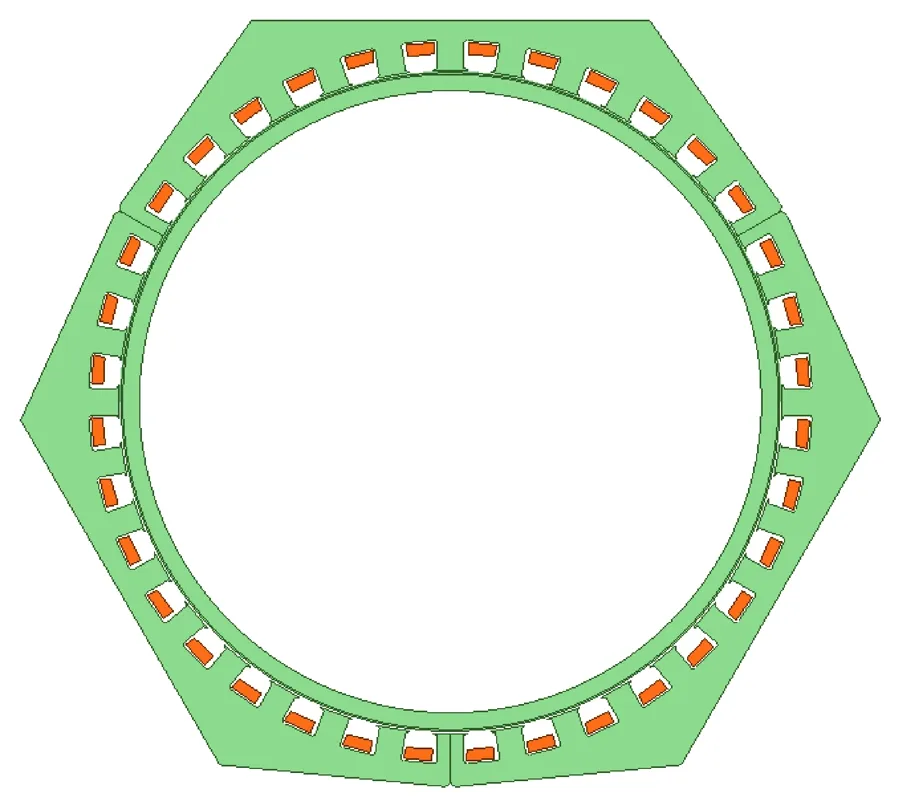
图10 整圆电机模型

在相同的15 mN·m时，对原电机和整圆电机(120 Hz、1.5 A)进行稳态仿真，表2为两电机仿真计算结果比较，图11为两电机稳定运行时在360°机械角度范围内的气隙磁密分布。可以看出：

(1)在相同负载转矩下整圆电机的稳定运行转速可以达到2 094 r/min，而原电机的稳定运行转速只有1 355 r/min，这显然是球形感应电机铁心磁极分断所造成；

(2)由图11可以看出，原电机在磁极铁心范围内的磁动势是整圆电机的3/2，但气隙磁密却比后者具有较大的降低，主要原因是前者由于铁心开断，产生端部效应，使电机转子转速降低，从而有较高的转差率，也就有较高的转子反应；

(3)原电机与其对应的整圆电机相比，具有更低的功率因数和运行效率。

表2 原电机与整圆电机在(120 Hz、1.5 A)组合时的性能比较

图11 原电机与整圆电机在(120 Hz、1.5 A)时的气隙磁密波形

原电机改成整圆后，在(115 Hz，1.5 A)组合下就可以达到15 mN·m、2 000 r/min的额定运行状态，其相关性能如表3所示，图12为此时的气隙磁密波形。与表1中的原电机最低工作频率(160 Hz)时的相关性能比较可以看出，总损耗由40.4 W降低为30.1 W，其中转子铜耗由31.8 W降低为21.68 W，是损耗的主要降低分量。由此也可以看出，由于球形感应电机定子磁极铁心分断，会产生很大的转子铜耗，因此降低铜耗成为球形感应电机降低损耗的关键。

表3 整圆电机在最低频率下产生15 mN·m、2 000 r/min时的相关性能

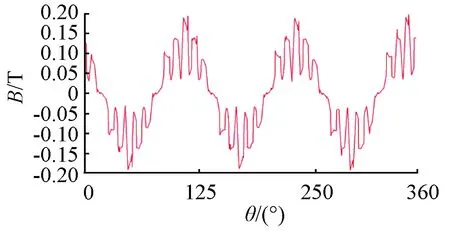
图12 整圆电机在最低频率下产生15 mN·m、2 000 r/min时的气隙磁密分布

4 浮转一体球形感应电机的悬浮特性分析

前面分析了球形感应电机的旋转特性，由于浮转一体球形感应电机的旋转驱动电流和悬浮电流是同一个电流，因此本节在前述旋转特性分析的基础上，分析其悬浮特性。前述分析时，同一旋转自由度的两个相对磁极绕组中的电流相同，但是在分析悬浮特性时，由于采用磁悬浮的差动控制方式，两个相对磁极绕组中电流的相同部分为偏置电流I0，但总电流不同，即两个磁极绕组中的总电流是在偏置电流I0的基础上分别加上和减去相同的控制电流ΔI。

本节分析包括以下内容：

(1)以前述旋转运行不同(Is，f)组合为基础，分析计算其悬浮特性；

(2)考虑球形感应电机的悬浮，使同一旋转自由度的两个相对磁极绕组中的电流有所不同，需要分析这一电流不同对电机旋转的影响，同时需要研究如何弥补这一电流不同对电机旋转的影响。

4.1 不同(Is，f)组合下的悬浮特性分析

以表1给出的(1.52 A，160 Hz)和(1.11 A，180 Hz)两种组合为基础，进行球转子在平衡位置时的电机悬浮特性分析。在分析悬浮特性时，上述组合中电流Is=1.52 A和1.11 A为偏置电流I0，在偏置电流基础上施加控制电流ΔI。在分析时，为了考虑电流频率对悬浮特性的影响，再加一组合(1.11 A，160 Hz)(该组合时如果不加控制电流，球形感应电机不能满足额定运行要求)，即在保持电流I=1.11 A不变时，比较分析频率f分别为160 Hz和180 Hz时悬浮特性的差异。表4、表5为相关计算结果，图13为表4的曲线表示。由表4及图13可以看出，旋转运行电流(悬浮偏置电流)和电流频率都对悬浮有影响。保持偏置电流有效值不变，降低电流频率，有利于提高悬浮力。

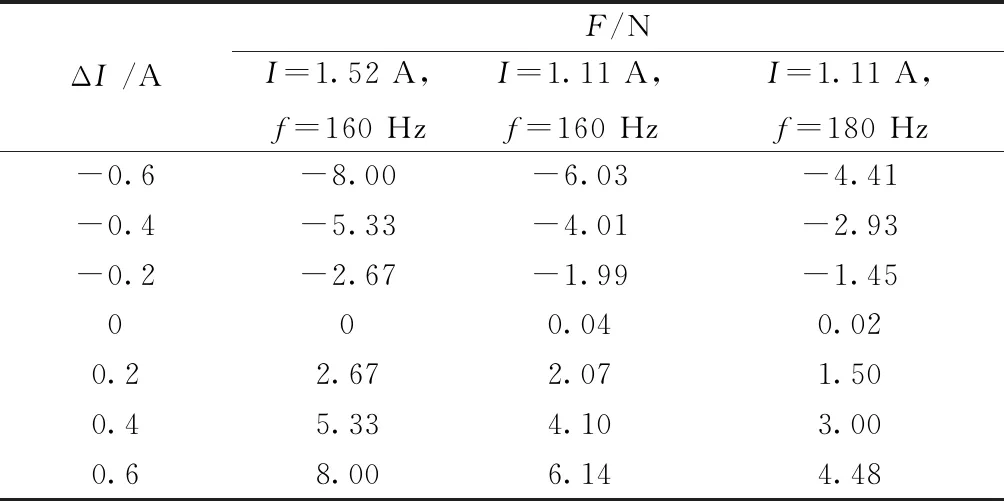
表4 不同旋转运行(Is，f)组合时的悬浮特性比较数据

图13 不同旋转运行(Is，f)组合时的悬浮力特性曲线

图14给出了(1.52 A，160 Hz)组合时悬浮力-电流-位移特性，表5是相关数据结果。可以看出，在平衡位置，1.3 A的控制电流能够满足18 N的悬浮力要求，在球转子最大偏移0.1 mm位置，0.7 A的控制电流就能够起浮12 N的球转子。同时由图14可以看出，球转子无论在平衡位置还是在最大偏移位置，都具有良好的线性悬浮力-电流-位移特性。

表5 (1.52 A，160 Hz)组合时悬浮力-电流-位移特性

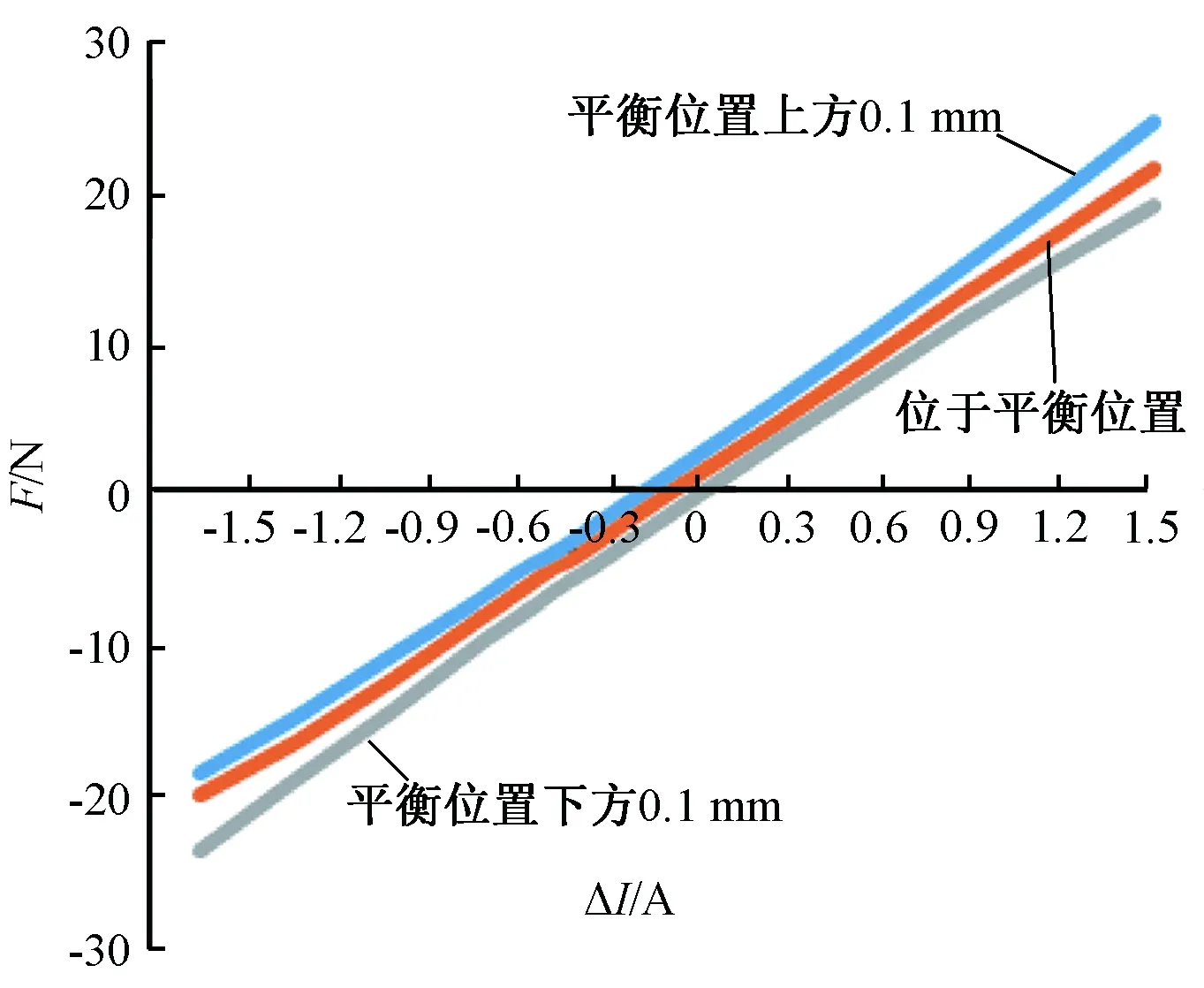
图14 (1.52 A，160 Hz)组合时悬浮力-电流-位移特性

4.2 差动悬浮对电机旋转特性的影响

以(1.52 A，160 Hz)组合状态为基础，在平衡位置，通过改变控制电流ΔI的大小，在保持转速为2 000 r/min时，电机的驱动转矩与ΔI的变化关系如图15所示，相关数据如表6所示。可以看出，随控制电流ΔI的增大，驱动转矩增大。由图5给出的相同频率下不同电流下的转矩-转差率特性可以看出，其最高转矩与电流的平方成正比，假定在转差率在0～sm范围内，转矩成线性变化，在固定转速2 000 r/min时，电机每个磁极产生的电磁转矩也与电流的平方成正比，即两个磁极产生的电磁转矩分别与(I+ΔI)2和(I-ΔI)2和成正比，即两个磁极中一个磁极电磁转矩增大，另一个角铁电磁转矩降低，但是增大的电磁转矩值大于降低的电磁转矩值，因此合成的电磁转矩增大。

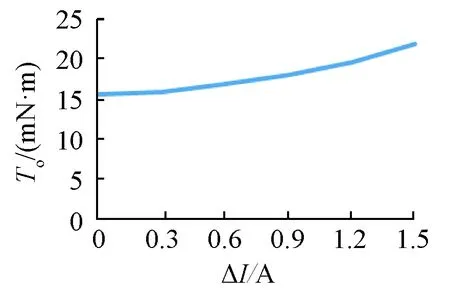
图15 差动悬浮对电机驱动力矩的影响

表6 差动悬浮对旋转驱动转矩的影响数据表

显然，在低悬浮力要求时，控制电流ΔI较小，悬浮驱动对旋转转矩的影响较小，特别是在太空应用时，球形感应电机处于失重状态，所要求的悬浮力很低，此时悬浮控制对旋转驱动影响可以忽略不计。但在地面试验时，要求具有较高悬浮力，悬浮控制影响到旋转驱动。

表7给出了上述计算算例中两个磁极分别产生的电磁转矩大小。可以明显看出，电流增大和电流降低对电磁转矩的不同影响，即在偏置电流的基础上，叠加正控制电流的磁极产生的电磁转矩的增加量，大于叠加负控制电流的磁极产生的电磁转矩的降低量，控制电流越大，这一差值就越大。

表7 不同控制电流对两角铁驱动电磁转矩的影响

同时比较表7和表6可以看出，分别计算两个磁极电磁转矩合成得到的总电磁转矩与同时计算两磁极得到的总电磁转矩具有差异，控制电流越小，差异越明显，随控制电流接近偏置电流，两者结果接近。其原因在于两个磁极之间的耦合关系。图16为两磁极同时通电和单独通电时的气隙磁密分布。比较图16(a)和图16(c)可以看出，两个对应磁极中，对方磁极绕组通入电流对己方磁极气隙磁密造成影响；但在控制电流较大时，对方磁极绕组总电流已很小，对己方磁极的气隙磁密影响很小(图16(b)和图16(d)为相同的状态，对方角铁绕组中的总电流为0)。

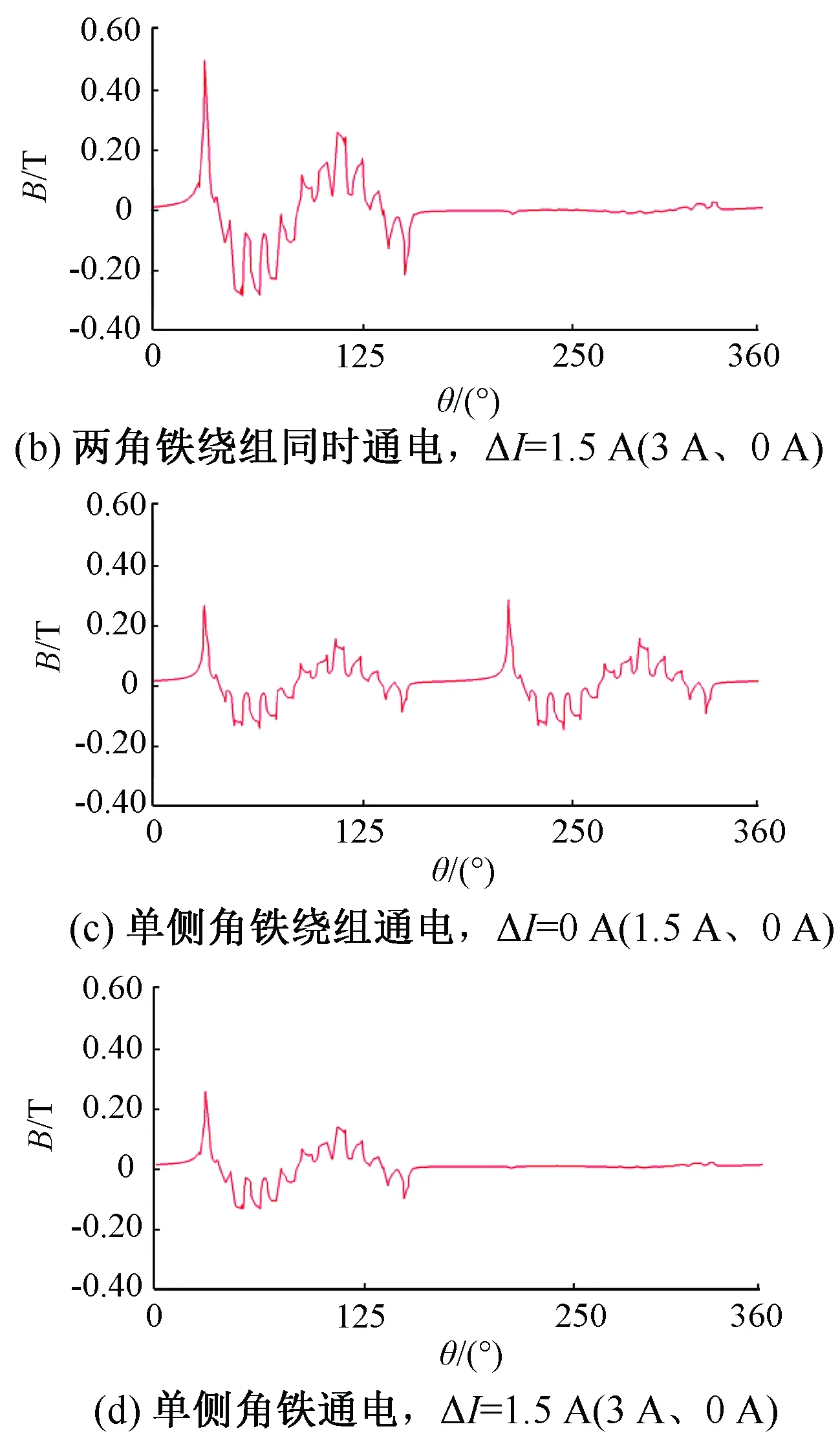
图16 两对应角铁同时或单独通电时气隙磁密分布

5 浮转一体球形感应电机(Is，f)组合的选择

由前述分析可以看出，在只考虑旋转驱动不考虑悬浮驱动时，电机电源频率和电流有效值都影响到电机的旋转驱动，但为了满足额定输出转矩和额定转速，电机电流的频率不能太低，这导致电机的转差率较高，尽管高转差率对球形感应电机的转差损耗影响较小，但降低了电机的过载倍数，这对电机的稳定旋转不利。

在只考虑悬浮驱动时，电机的电源频率和电流影响到电机的悬浮，特别是相同电流下，频率降低有利于提高电机的悬浮力。

如果同时考虑球形感应电机旋转驱动和悬浮驱动，悬浮驱动在一定程度上有利于提高电机的旋转转矩，即在同时考虑悬浮和旋转时，可以降低电机电流的运行频率，而且电机电流运行频率的降低又有利于提高电机的悬浮力，从而降低电机的控制电流，有利于降低电机的整体功耗。因此，对浮转一体球形感应电机来说，电机的偏置电流、控制电流及电流频率需要协调给定，才能在同时满足旋转驱动和悬浮驱动的要求下具有最好的其他性能。

6 结 语

本文对浮转一体球形感应电机的旋转驱动及悬浮驱动进行了理论分析和电磁场有限元分析计算，得到以下主要结论：

(1)基于电流源驱动的浮转一体球形感应电机，满足相同的额定旋转运行，可以有不同的(Is，f)组合，各运行组合具有不同的功耗和过载能力，在各运行组合的功耗构成中，转子铜球功耗最高、定子铜耗次之，而定、转子铁耗较低；随频率降低，电流、功耗及过载能力增大，但由于各旋转自由度两相对磁极的开断结构，影响到电机的性能，因此运行频率不能太低；在相同电流容量下，降低频率，有利于提高电机的悬浮能力。

(2)差动悬浮对电机的旋转驱动具有重要影响，满足球电机的高悬浮力要求的同时，可以提高电机的旋转驱动能力。

(3)浮转一体球形感应电机的旋转驱动和悬浮驱动都与电流源的频率、电流有效值有关，而且旋转驱动和旋转驱动性能彼此相互影响，因此浮转一体球形感应电机的驱动应该综合优化旋转驱动和悬浮驱动，才能得到最优电机性能。