基于局部密度的最小生成树聚类算法及其在电力大数据的应用

靳文星，王电钢，张哲敏

(1.上海电力大学计算机科学与技术学院，上海 200090；2.国网四川省电力公司信息通信公司，四川 成都 610041)

0 引 言

近些年，针对电力大数据收集和存储中数据量大、数据收集不精准的问题,先后提出并采用了K-means、K-medoids[1]和一些改进之后的K-means算法，但是这些算法的使用都必须初始化聚类中心。为了避免初始化聚类中心，在算法领域中的AP算法[2]将所有数据点都视为潜在的中心。K-AP[3]是AP算法的改进，它在消息传递过程中引入约束，利用K簇产生的直接结果，然而，由于每个点总是分配到最近的中心，导致这些算法不能发现任意形状的聚类(即类簇)。还有一种快速搜索发现密度峰值[4](density peak，DP)的聚类算法，选择局部密度最大的点作为聚类中心，将其余点作为密度最大的近邻分配到同一个类别中。假设每个类簇都有收缩的密度核，大致保留了类簇的形状，并提出了一种基于密度核的聚类算法，称为Dcore[5]。基于密度的聚类算法DBSCAN[6]将聚类定义为由稀疏区域分隔的稠密区域。它的关键思想是，设定集群的每个核心点，在每个核心点周围给定半径内必须包含有参数设定数量的点(如参数设定为30，则若一点给定半径范围内有超过30点，即认定此点为核心点)。Dcore和DBSCAN可以有效地识别具有任意形状的数据集，但是它们必须设置许多参数。

针对电力大数据中无法高效识别具有任意形状数据集的问题，提出了基于最小生成树(minimum spanning tree，MST)和局部密度峰值(local density peak，LDP)的聚类算法，称为LDP-MST，它在发现复杂数据时，不仅计算效率高，而且可以与其他先进的聚类方法相媲美。在LDP-MST中，首先找到局部密度峰值，将剩余的点分配到相应的局部密度峰值；然后，定义一个新的基于共享邻点的局部密度峰值之间的距离，并利用新的距离在局部密度峰值上构造最小生成树；最后通过不断地去除最长边，得到了最终的聚类。

1 基于局部密度峰值和共享邻点的MST聚类

现有的基于MST的聚类算法，在整个数据集上构造MST的时候，因为只利用树中包含的边缘信息对数据集进行划分，导致数据的计算量很大，而且容易受到噪声点的影响。基于此问题，提出了一种基于局部密度峰值的最小生成树聚类算法(以图1所示的一个数集为例)。首先，选取相邻区域中局部密度最大的点作为局部密度峰值，并将其余点分配到相应的局部密度峰值附近，如图1(a)所示；然后，定义一个新的局部密度峰值之间的距离分类(它考虑了欧几里得距离和邻点信息)，利用局部密度峰值和距离构建MST，如图1(b)所示。在此之后，根据新的距离不断地去除最长的边，并进行距离连线，直到得到期望的簇数。图1(c)中链接不同簇之间的边是需要从MST中更正的边，最后得到如图1(d)所示的聚类结果。整个算法过程由于只在局部密度峰值上构造MST，减少了噪声点的干扰，大大提高了算法的效率。

图1 LDP-MST的主要思想

1.1 局部密度

为了找到局部密度峰值，首先定义点的局部密度。因为稠密区域的点与其近邻点的距离总和通常小于稀疏区域的点与近邻点的距离之和,在稠密区域，nb值较大；在稀疏区域，nb值较小，所以，点p的局部密度与nb(p)的值成正比，与点p和其相邻点之间的距离成反比。利用这一特性，计算局部密度ρ(p)：

式中：nb(p)为到达自然特征值时的p的反向近邻数；NNK(p)为p的反向k近邻；d(p,q)为p和q之间的距离。

如图2中给出了每个局部密度峰值的邻域(图中粗线表示)，其中包括其成员和一些额外的最近邻域，在图中用不同点间的连线表示。共享邻点的数量和密度越大，表示它们之间的距离越小。

图2 LDP的邻点和共享邻点

1.2 基于共享邻点的局部密度峰值之间的距离

由于欧几里得距离不能很好地对复杂数据进行恰当度量，且由于大多时候都测量不到图形点位置的先验信息，导致不能直接得到准确的测量距离。基于局部密度峰值的共享邻域，采用了一个新的距离，即基于共享邻点的局部密度峰值之间的距离。

由于数据集中局部密度峰值分布不均匀，欧氏距离不适用于测量局部密度峰值之间的差异。所以使用基于邻域的共享距离利用局部密度峰值之间的邻域信息，缩短被稠密区域紧密相连的局部密度峰值之间的距离的方法更恰当地表示了局部密度峰值之间的差异。

以图3所示的数据集为例，图3(a)为局部密度峰值及其邻域点，图3(b)为用欧几里得法构造的局部密度峰值的MST图像，图3(c)为基于共享邻点的距离构造的MST图像。局部密度峰值p和q在同一簇，q和o在不同簇，但是p和q之间的欧氏距离大于q和o之间的欧氏距离，所以用欧氏距离构造的MST会出现错误。但是，基于共享邻点的距离构建的MST正确地保留了原始数据集的结构。

图3 各个方法距离的区别

1.3 算法流程

首先，使用局部密度峰值和基于共享邻点的距离来构建MST；然后，重复切割最长的边(边的长度是采用基于共享邻点距离的)，并保证切割该边导致的两个簇的大小都大于松散估计的最小点数，直到找到给定数量的簇为止。对局部密度峰值进行聚类后，将每个剩余点分配到与对应的局部密度峰值所属的相同类簇中。LDP-MST算法主要包括以下步骤:1)搜索局部密度峰值;2)计算局部密度峰值之间基于共享邻点的距离;3)采用基于MST的聚类算法对局部密度峰值进行聚类。

2 LDP-MST在电力大数据中的应用

如今，智能电网建设速度不断加快，与之而来的是大量的数据，这些数据主要来源于电网的发、输、配、用四大环节。聚类分析可以从大量的、不完全的、有噪声的、模糊的、随机的数据中，提取隐含在其中的人们事先不知道但又具有潜在价值的信息。其中，最具有显著效果的聚类分析就是对用户用电行为的聚类和异常检测。用户用电行为聚类基于用户用电行为模式对相似性用户进行划分类别，而异常检测主要是指检测电力偷窃、电能表错误、计费错误等非技术损失造成的异常用电情况。

LDP-MST算法在电力大数据领域具有良好的应用前景，尤其体现在异常值检测中。异常值检测的目标是将不属于任何簇的样本点与正常点进行区别，从数据的角度来说，就是找出样本点数量较小的簇。故使用LDP-MST算法将样本点较少的簇提取出来，就可以得到异常样本。为验证算法的实用性，以某网站3个月的访问量和网络流量为基础，使用LDD-MST算法检测了其中的异常值。

在进行聚类之前，先对数据进行了预处理，即用缺失点外的其他值的均值代替该属性的缺失值。最终得到LDP-MST算法聚类结果如图4所示。由于只通过聚类法不容易用肉眼判别聚类结果，所以要对数据进行归一化处理。这里采取的归一化的方式为图5为归一化处理后的数据。由图可以看出，在3月之初以及4月中后期有一些数据的网络流量与正常用户访问次数差距较大，明显偏离了正常数值。将这些异常值输出，并经聚类分析和异常值判定后，得到如表1所示的异常值分布。可发现所提算法将数据集中的异常值全部检测出来，说明LDP-MST算法对异常值检测具有比较良好的效果。

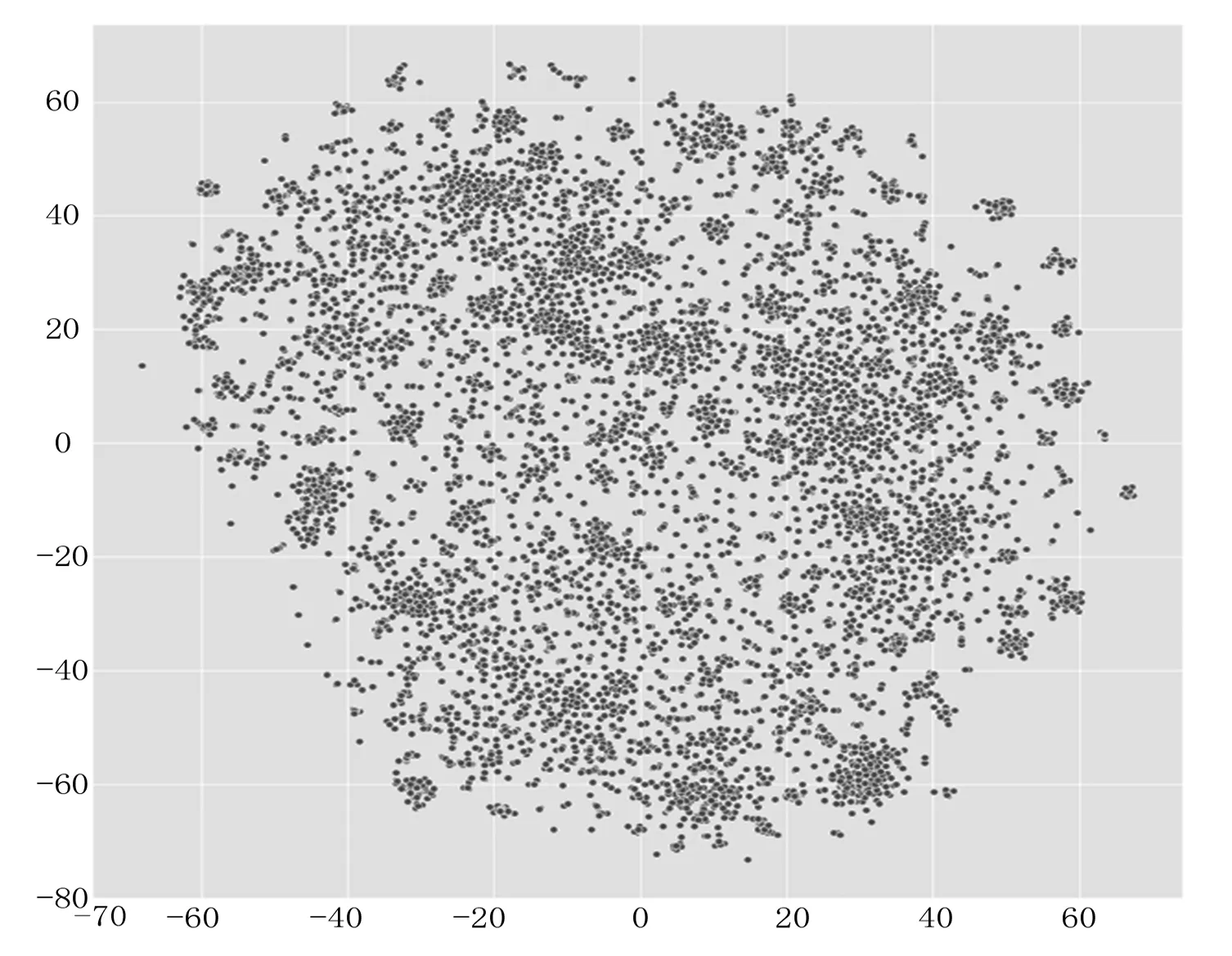
图4 LDP-MST算法聚类结果

图5 归一化处理后的数据分布

表1 异常值数据分布

3 结 语

上面提出了一种新的聚类算法LDP-MST，其核心思想是选择局部密度峰值来构建MST，避免了噪声点的干扰，减少了基于MST的聚类算法的运行时间。电力综合数据集的实验表明，该聚类算法能较好地识别数据集中的复杂模式，且比现有的聚类算法更有效。在进行电力大数据的异常检测时，算法在短时间内有效地检测出了异常结果。今后，将继续完善本算法的缺点以及将这一基于聚类算法的异常检测方法应用到电力系统的更多方面。