循环荷载作用下泥岩动力特性

龙 慧,刘书文,庄 轲,梁海安

(1.南华大学 土木工程学院,湖南 衡阳 421001;2.东华理工大学 土木与建筑工程学院,江西 南昌 330013)

0 引 言

随着经济的发展与社会需求，越来越多的大型工程正在或将要兴建，这些建(构)筑物在使用过程中很可能受到地震作用、冲击荷载等动力荷载的作用。在实际工程中，泥岩是一种较为常见的地基土体，与一般土质地基相比，泥岩质地基承载力相对较高，但泥岩属于软岩，其力学性质较为特殊，为了更好的研究泥岩在地震作用、冲击荷载等动力荷载下的动力性能，保证工程的安全性，需对循环荷载作用下泥岩的动力特性进行深入研究。

段东等[1]利用CT图像和声发射技术，较好地反映出不同加载阶段试件中微裂纹闭合、扩展、分叉等细观损伤活动及岩样内部微破裂、微裂纹的演化过程；王传洋、段东[2-3]等对泥岩进行了单轴压缩下的同步CT 扫描试验，描述了不同荷载水平下，泥岩细观下裂纹演化与宏观的变形特性；王春等[4]基于高轴压与围压的试验条件，分析了围压对岩石动应力-应变曲线及岩石破坏加载次数的影响。

范秋雁等[5]通过单轴压缩无侧限蠕变试验和有侧限蠕变试验并配合扫描电镜来分析泥岩的蠕变特性，实验结果表明岩石的蠕变是岩石损伤效应与硬化效应共同作用的结果;刘海壮、吴仲衡等[6-7]分别通过试验与数值模拟，分析了泥质砂岩在不同围压条件下的应力-应变曲线及岩石的破坏形式，吴仲衡指出随着围压的提高，岩石变形从脆性破裂向脆-塑变形(共轭裂缝)转化。李福林等[8]通过对泥岩在 4 种不同加载速率(0.005、0.05、0.5 和 3 mm/min)下进行的系列性单轴压缩试验，表明泥岩具有明显的加载速率变化效应且表现为等速黏性特性。

蔡国军[9]等使用MTS815岩石力学试验机在频率为1 Hz的条件下对泥岩进行7级循环加卸载试验，发现泥岩动弹性模量随着循环级数的增加逐渐减小，阻尼比则反之; 王金鹏等[10]同样使用MTS815岩石力学试验机研究了单轴循环荷载作用下泥岩与页岩滞回面积、动弹性模量及阻尼比与循环加卸载次数间的变化关系；邓华峰等[11]则通过岩石的单轴加卸载循环试验，探究了在加卸载过程中能量及损伤演化规律，并提出了在残余应变及滞回效应的影响下，各能量参数在循环加卸载过程中的修正方法；潘旦光、陈钒等[12-13]对饱和泥岩进行了变幅分级循环荷载试验，在变幅分级循环加载阶段，阻尼比与动弹性模量都随动应力幅值的增加而增加;王轲等[14]在MTS815岩石力学试验系统上对饱和泥岩与饱和砂岩进行变幅分级循环荷载试验，发现应力幅值不变时，随着循环次数的增加，阻尼比趋向于稳定，应力幅值越大，阻尼比越大;何明明等[15]研究了动弹性模量与应力幅值间的响应，建立了耗散能演化模型来描述循环荷载下能量耗散行为并提出阻尼参数的计算方法;刘建峰[16]等利用 MTS815 Flex Test GT 岩石力学试验系统，对细砂岩和粉砂质泥岩进行单轴压缩循环荷载下的试验研究，发现岩石的加卸载循环塑性变形、滞回环面积、阻尼比、阻尼系数与岩石密度间的相关性。

已有对岩石动力特性的研究更多专注于高围压下岩石的强度与稳定性，或高频激励下岩石的率效应，而多数情况下建(构)筑物基础的埋深不大(如核电站)，岩体多处于低围压状态。因而本文选取0.5 MPa和1 MPa作为岩样施加的围压，同时湖南省内及周边无活跃近断层，所受地震风险以低频成分较多的远场地震动为主，所以取0.2 Hz～2 Hz为岩石的加载频率。在低围压状态下对其施加循环荷载，研究泥岩在低围压低频循环荷载作用下的岩石的破坏形式特性、动强度(模量)及滞回曲线面积特性。相关研究可为浅埋基岩建构物的选址及抗震设计提供理论依据。

1 实验概述1.1 岩样制备

试验岩样采自于湖南浏阳市，岩样为褐色块状结构，泥质胶结，中-强风化。岩石样品为标准岩样即Φ50 mm×100 mm进行加工，岩石样品高度与直径误差分别小于2 mm和0.3 mm，且岩石端面偏离轴向角度小于0.25°。样品误差满足《工程岩体实验方法标准(GB/T50266—2013)》对岩体样品的要求。为减少对试样的扰动以保证试验质量，岩样全程由保鲜膜包裹以减少水分蒸发对岩样抗压强度的影响。

1.2 试验设备及步骤

如图1所示，试验仪器采用东华理工大学的微机伺服岩石三轴试验机TAW-2000，该仪器最大试验力：2000 kN；有效测量范围：在最大试验力的2%～100%范围内，测力精度≤±1%示值；围压系统：最大围压100 MPa，测力精度≤±2%示值；轴向变形范围：0～5 mm，径向变形范围：0～3 mm，测量精度≤±1%示值。试验设备能够较好地满足该实验的实验要求，保证试验的顺利进行。

试验过程中需要对岩样进行编号处理。以编号为M-A1岩样为例，用泥岩单词的首字母“M”表示泥岩，“-A1”为编号，具体见表1。加载过程中，振幅从0 kN开始进行循环加载，每级振幅增加2，循环5次，每个循环结束回到0 kN；轴压通过控制位移的方法实现加载；加载围压主要通过围压室液压油施加围压，频率为余弦函数形式，通过微机控制，当岩样压坏时，停止试验。

2 试验结果

2.1 岩石破坏特征

如图2所示，当围压为0.5 MPa时，岩石破坏形式随频率的变化较大，随着频率的提高，由剪切破坏向劈裂破坏过渡。这是由于此时围压较低，当加载频率提高后，岩石上端加载面产生了较大的动力变形，在端部摩擦力的约束下(即端部效应影响)，应力在局部集中形成类似刚性楔(图2(a)中上端三角形)，并向下劈裂。因此，当建筑在使用过程中可能受到较大的冲击荷载(如大型设备振动)作用时需要防止浅埋泥岩地基出现这种破坏。当围压为1 MPa时，则以水平向的剪切破坏为主。

图2 岩石受压破坏照片Fig.2 Photos of rock failure under compression

如图3所示，泥岩的应力-应变曲线主要分为四个阶段。OA段为微裂隙压密阶段，在荷载加载初期，岩石内部微裂隙、裂缝等缺陷被压缩挤密，曲线下凹，形成早期非线性变形；AB段为弹性变形阶段，岩样中原有裂隙继续被压密，与之前相比，岩石内部缺陷减少，使材料更为理想，此阶段内认为岩石的应力与应变同步增长，故在轴力的作用下，曲线接近一条直线；BC段为裂隙的发生、扩展直至破坏阶段，在荷载的持续加载过程中，形成新的微裂缝，加载方向裂隙不断发展，裂隙进入不稳定发展阶段，裂隙扩展交接形成滑动面，导致岩石试件完全破坏；CD段为不稳定阶段，岩样通过峰值强度后，结构遭到破坏，试件基本保持整体形状，此后岩石变形主要表现为沿宏观断裂面的块体滑移，其承载力降低较快，但并不降为零，说明岩石破坏后仍有一定的承载力。

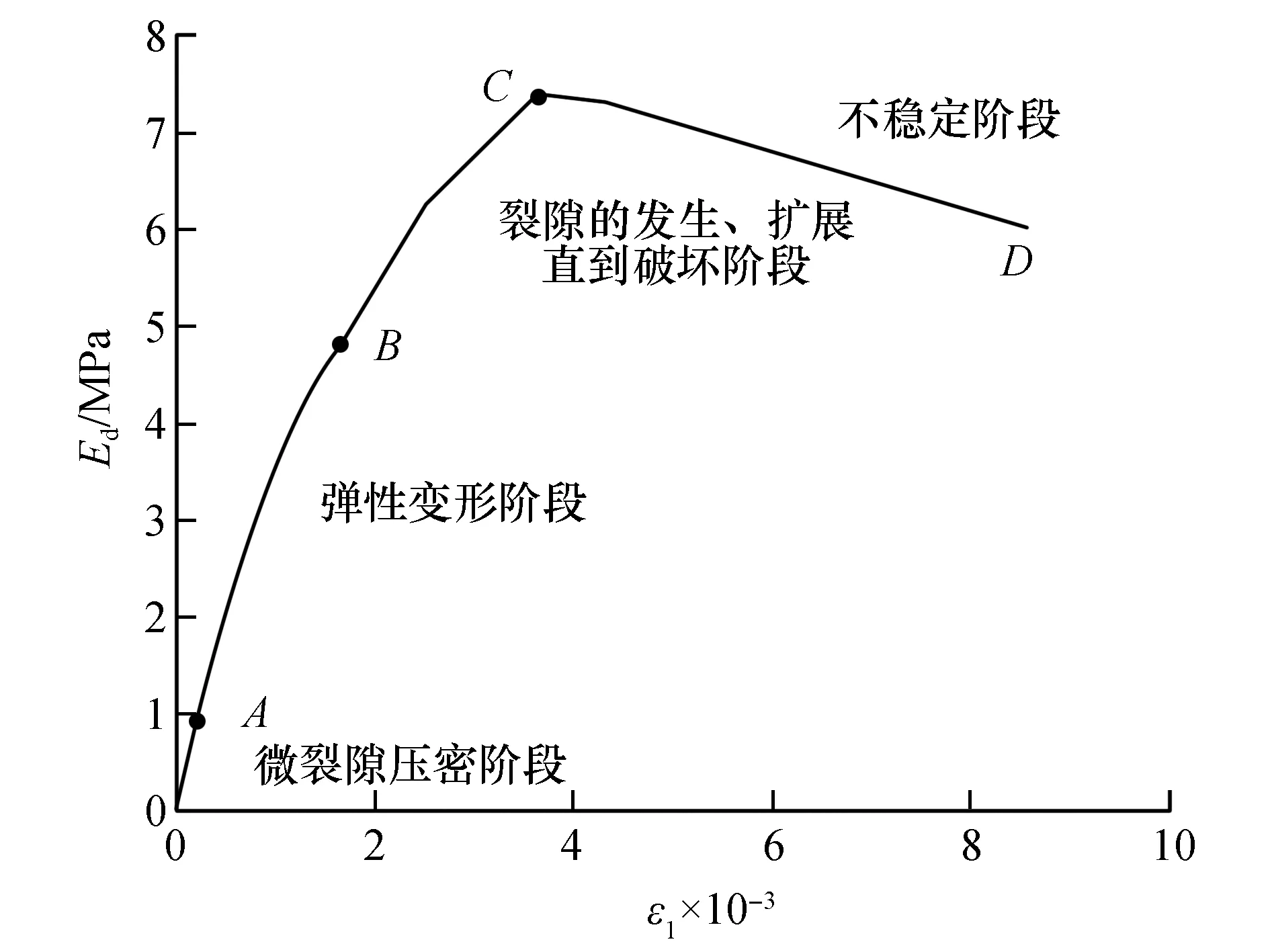
图3 泥岩应力-应变曲线(σ3=0.5 MPa，f=0.5 Hz)Fig.3 Stress strain curve of mudstone (σ3=0.5 MPa，f=0.5 Hz)

2.2 岩石动抗压强度

如表1所示，泥岩的动抗压强度，在0.2 Hz～1 Hz范围内，主要呈现减小趋势，主要是由于泥岩强度较低，在较低的加载频率下，其动力响应较为显著，岩石变形较大，导致泥岩动抗压强度略低于静抗压强度；当频率达到2 Hz时，泥岩的率效应较为显著，且随着围压的提高，动抗压强度均有较大提高。

表1 泥岩基本物理参数Table 1 Basic physical parameters of mudstone

由实验结果可知，岩样M-B1和M-C2抗压强度明显低于岩石其他岩石抗压强度，可能是其内部存在节理造成的，故岩石抗压强度较低，在进行数据分析时，并未考虑这两个岩样。如表1所示，岩样(M-B1)的抗压强度明显较小，主要是岩石是一种不连续非均质多空材料，其内部可能存在缺陷，导致其力学实验结与其它岩样数据产生较大的离散性，故在进行数据分析时，并未考虑岩样(M-B1)的影响。岩的单轴抗压强度为8.18 MPa；当σ3=0.5 MPa,f=0.5 Hz、1 Hz、2 Hz时，与泥岩静抗压强度对比，在0.5 Hz、1 Hz范围内，动抗压强度分别降低了8.2%和3.1%，在2 Hz时，动抗压强度提高了53.5%；当σ3=1 MPa,f=0.2 Hz、1 Hz、2 Hz时，在0.2 Hz、1 Hz范围内，与泥岩静抗压强度对比，动抗压强度分别降低了0.005%和12.1%，在2 Hz时，动抗压强度提高了68.9%。可见在1 Hz范围内，加载频率对泥岩抗压强度总体影响不大，而在加载频率达到2 Hz时，岩石动强度有明显提高。

2.3 应力-应变滞回曲线

以围压为0.5 MPa、加载频率为0.5 Hz的岩样为例，如图4所示。在循环荷载作用下，随着荷载的增加，滞回曲线面积明显增加，并向应变增大方向移动。同一级加载水平下，随着循环次数的增加，滞回曲线向应变增大方向平移，说明在同一级加载水平下，每次加卸载作用下，泥岩均产生了不可恢复的变形。

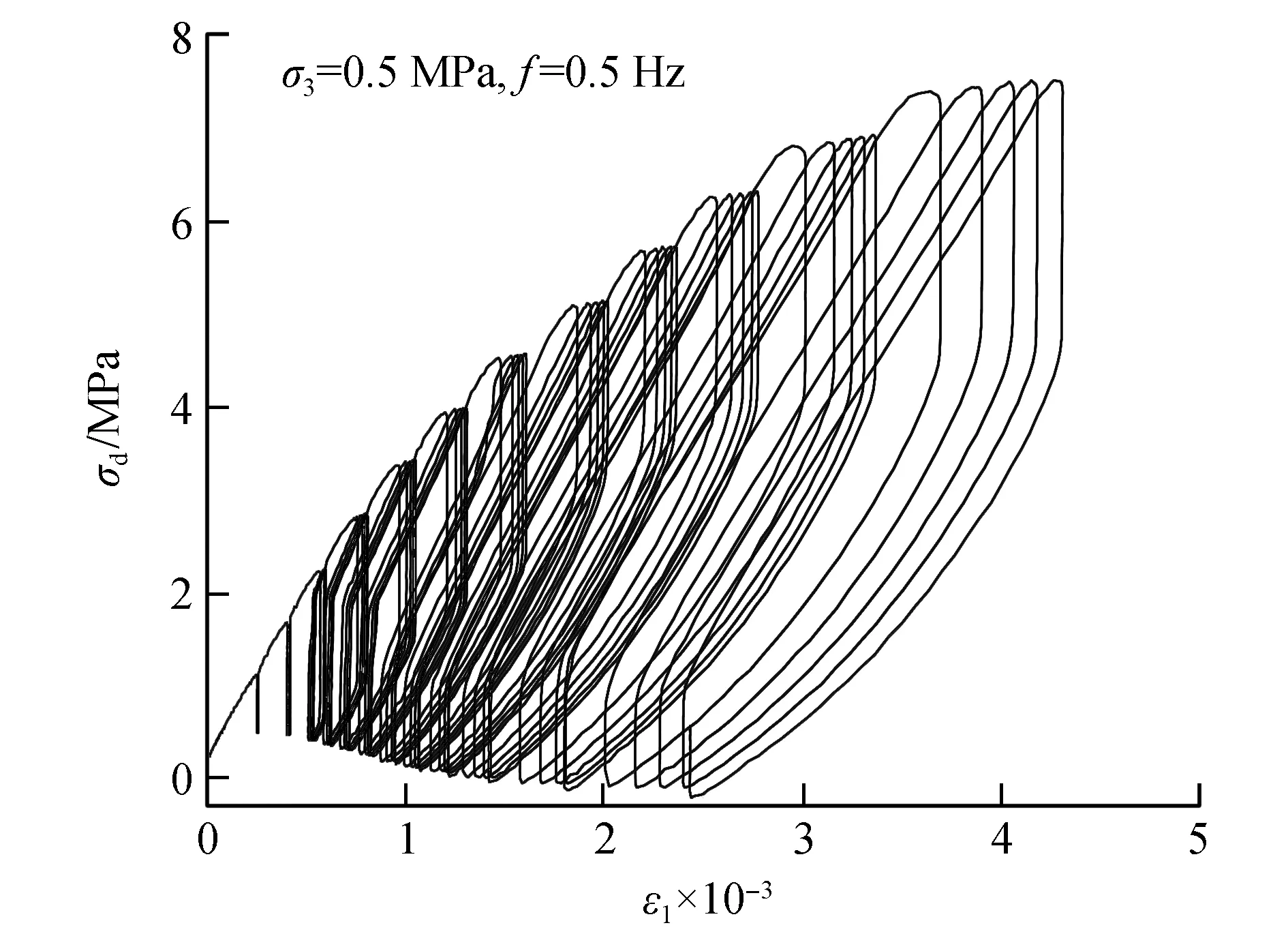
图4 循环荷载作用下岩石应力-应变曲线Fig.4 Stress strain curve of rock under cyclic loading

如图5(a)所示，在围压相同的条件下，随频率的增加，滞回曲线面积与频率间并无明显的相关性；在0.5 MPa～1 MPa的围压下，滞回曲线面积与围压间并无明显的相关性。

如图5(b)所示，泥岩在同一级加载幅值下，随循环次数的增加，滞回曲线面积逐渐减小，且第一次循环下，滞回曲线面积均明显大于第2～4次循环时的面积。同样，第一次循环下，滞回曲线的残余应变均也明显大于第2～4次循环时的残余应变，第一次循环作用下滞回环残余应变较大的现象与张媛[17]实验具有一致性。滞回曲线面积的大小与岩石耗能和内部疲劳损伤的大小有着正相关性。由此可知，泥岩随着加载幅值的增加，泥岩的能量耗散与损伤不断加剧。在同一级加载幅值作用下，能量的耗散与损伤随循环次数的增加呈减小趋势，在加载阶段面积随着循环次数的增加而逐渐减小，卸载阶段面积随循环次数的增加而增大并趋于稳定，故滞回环面积随循环次数的增加而逐渐减小[17]。

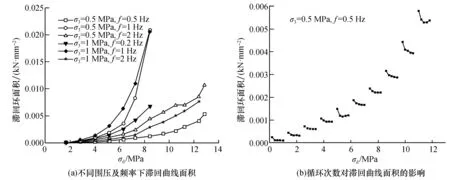
图5 循环荷载及频率作用下岩石滞回曲线面积Fig.5 Hysteretic curve area of rock under cyclic load and frequency

2.4 动弹性模量Ed

动弹性模量与阻尼比的计算公式[18]如下：

A：图6中ABCDA面积，反应了岩石在加、卸载作用下，能量损耗大小；AS:△AFE面积，代表峰值所对应的弹性能。

图6 循环荷载作用下应力-应变曲线Fig.6 Stress strain curve under cyclic loading

在加载初期，泥岩动弹性模量波动较大，故部分岩样未取加载初期动弹性模量。如图7所示，在0.5MPa～1MPa的围压下，加载频率为0.2Hz～2Hz的条件下，泥岩的动弹性模量均随加载幅值的增加逐渐减小,与蔡国军[9]实验结果具有一致性。同一围压作用下,Ed随频率的增加，无明显改变。在加载初期，随着围压的增加，Ed普遍高于低围压下的岩样；随着加载幅值的增加，0.5MPa与1MPa下的岩样Ed并无明显差别；随着加载幅值的增加，Ed先减小后趋于3 600MPa至3 800MPa区间内(σ3=1MPa,f=2Hz的泥岩除外)，直至破坏。

图7 循环荷载作用下Ed-加载幅值曲线Fig.7 Curve of dynamic elastic modulus and loading amplitude under cyclic loading

3 结 论

1)在0.2Hz～2Hz循环荷载及不同围压作用下，岩石破坏形式有所不同；当围压为0.5MPa时，岩石破坏形式随频率的变化较大，随着频率的提高，由剪切破坏向劈裂破坏过渡；当围压为1MPa时，岩石以剪切破坏为主。

2)在0.5MPa～1MPa的围压和0.2Hz～1Hz的加载频率下，泥岩动抗压强度峰值主要呈现减小趋势。当加载频率为2Hz时，随着围压的提高，泥岩动抗压强度均有较大提高。

3)围压由0.5MPa～1MPa的变化过程中，同一幅值作用下，滞回曲线面积随循环次数的增加呈现减小趋势；Ed先减小后趋于3 600MPa至3 800MPa区间内，直至破坏；滞回曲线面积和Ed在0.5MPa～1MPa围压下，其变化规律与加载频率无明显相关性。