基于SM2 数字签名算法的环签名方案*
范 青, 何德彪, 罗 敏, 黄欣沂, 李大为
1. 武汉大学 数学与统计学院, 武汉430072
2. 武汉大学 国家网络安全学院, 武汉430072
3. 福建师范大学 计算机与网络空间安全学院, 福州350117
4. 深圳技术大学 大数据与互联网学院, 深圳518118
1 引言
传统数字签名算法保证了数据完整性和签名者抗抵赖性. 国家密码管理局于2010 年12 月17 日发布了SM2 椭圆曲线公钥密码算法[1], 并于2012 年批准为密码行业标准(GM/T 0003-2012)[2], 2016年正式发布为中国国家密码标准(GB/T32918-2016)[3]. SM2 数字签名算法作为其中之一部分, 与基于有限域上困难问题的数字签名算法相比, 在相同的安全强度下SM2 数字签名具有存储空间小、签名速度快的优势. 在商用密码体系中, 该标准提供了电子认证服务系统所需的安全性能, 替代了国外的ECDSA、Schnorr 等签名算法, 推动了密码技术应用发展的自主化和可控性, 丰富了国产密码体系.
但是日益发展的信息安全技术对数字签名提出了新的功能性需求, 如电子现金、电子投票、匿名通信等具体的应用场景中, 要求用户的身份和位置等隐私信息保密. 环签名能够隐藏真实签名者的身份, 达到匿名性的效果. 2001 年, Rivest 等人首次提出了模糊签名者身份的新型签名概念——环签名[4]. 环签名是指签名者自发选择多个用户, 然后利用自身公私钥对和选取的用户公钥对文件进行签名. 签名者及其选择的用户组成的群组称为环, 构成环的成员由签名者根据所需指定, 验证者只能知道签名值出自环中某一成员, 但不能确定出真实的签名者. 环签名实现了将真实签名者的身份隐藏在环中, 以保护用户的身份隐私.
为深入理解环签名的概念, 下面给出环签名和群签名之间的联系与区别. 环签名和群签名均为个体代表群体签名的体制, 都实现了签名身份的匿名性. 但二者之间也存在着区别, 主要体现在以下三个方面[5–7]: (1) 管理系统: 环签名具有自发性, 环中每个成员地位平等; 群签名中存在一个管理员负责群成员的加入和离开. (2) 匿名特征: 环签名具有无条件匿名性, 即任何人在任何情况下都不能恢复出签名者的真实身份; 群签名的匿名性是有条件的, 群管理员能够根据签名得出签名出自群体中哪一个成员. (3) 签名密钥: 环签名的生成使用用户的密钥, 包括签名者私钥和环成员公钥; 群签名不仅需要用户密钥还需要群管理员的密钥.
环签名因其自发性和无条件匿名性得到广泛应用, 包括电子邮件、数据交换、电子交易和电子货币等领域[7]. 根据密钥生成方式不同, 环签名分为公钥基础设施(PKI) 体系下的环签名[4,8–16]、基于身份(IBC) 的环签名[17–23]以及无证书(CLC) 体系下的环签名[24–29]. PKI 体系下经典的环签名包含基于RSA 签名算法的RST 环签名算法[4]和基于Schnorr 签名的AOS 环签名[8], 但是尚未有公开可查询到的基于SM2 数字签名算法的环签名.
电子商务的广泛深入发展对环签名提出了多样化的应用需求, 根据不同的属性特征, 环签名分为可链接环签名[30]、可否认的环签名[31]、门限环签名[32]、可撤销匿名性的环签名[33]等等, 目前应用较为广泛的是可链接环签名. Liu 等人在2004 年首次提出具有自发性的可链接环签名概念[30], 并提出第一个可链接环签名方案——LSAG. 在环签名算法的基础上, 用户利用自身私钥生成一个关联此次签名的标签, 该标签不可伪造且同一签名者对不同消息生成的环签名具有相同的链接标签, 实现了对同一签名者所生成签名的链接. 在Liu 等人的文章中, 利用LSAG 构建的投票系统既能确保选民身份匿名性又能避免重复投票. 2013 年, Saberhagen 等人将可链接环签名应用于基于区块链的数字货币协议[34], 提出了适用于门罗币的CryptoNote 协议, 该协议有效保护了交易双方的身份隐私; 在此基础上, 出现了可链接环签名在区块链中的典型应用——RingCT1.0[35], RingCT2.0[36]和RingCT3.0[37].
为了弥补SM2 数字签名算法在环签名研究中的空缺, 奠定国产SM2 数字签名算法应用于区块链的基础, 进而把握区块链发展中密码技术的自主可控权, 本文基于SM2 数字签名算法提出了SM2 环签名方案, 并且通过嵌入安全的链接标签提出了SM2 可链接环签名方案及其两种变型方案.
本文结构如下: 第2 节介绍了环签名的预备知识, 包括环签名和可链接环签名的定义, 正确性、不可伪造性、无条件匿名性以及链接性、不可诽谤性等安全性要求, 同时介绍了SM2 数字签名算法; 第3 节提出了SM2 环签名的系统参数生成、密钥生成、(可链接) 环签名、环签名验证等4 个算法, 从系统参数生成、密钥生成、可链接环签名生成、可链接环签名验证、链接等5 个方面介绍了SM2 可链接环签名及其两种变型方案; 第4 节证明了SM2 环签名和可链接环签名的安全性; 第5 节分析了其通信成本和计算成本与环成员数量的关系; 最后在第6 节给出了本文的总结和展望.
2 预备知识
2.1 环签名定义与安全性
本节给出环签名的定义、安全性需求[38]以及椭圆曲线上的困难问题假设.
定义1 (环签名) 环签名包含4 个多项式时间算法: 系统初始化、密钥生成、环签名生成和环签名验证.
• 系统初始化算法(Setup(λ)→params): 一个概率多项式时间(PPT) 算法, 其输入为安全参数λ,输出系统参数Params.
• 密钥生成算法(KeyGen(λ, params)→(PK, sk)): 一个PPT 算法, 输入为安全参数λ和系统参数params, 输出用户的公钥PK 和私钥sk.
• 环签名生成(RSign(M,n,S,skπ)→σ): 一个PPT 算法, 其输入为待签名消息M、n个成员公钥组成的集合S={PK1,PK2,··· ,PKn}以及签名者私钥skπ(1≤π ≤n), 输出签名值σ.
• 环签名验证(RVerify(M,S,σ)→accept/reject): 一个确定性算法, 其输入为签名消息M、公钥集合S以及签名值σ, 若σ是M的有效环签名输出accept, 否则输出reject.
定义2 (可链接环签名) 具有链接性的环签名称为可链接环签名, 在环签名的基础上, 可链接环签名不仅包含系统初始化、密钥生成、可链接环签名生成、可链接环签名验证, 还包含链接算法.
• 系统初始化算法(Setup(λ)→params): 一个概率多项式时间(PPT) 的算法, 其输入为安全参数λ, 输出系统参数params.
• 密钥生成算法(KeyGen(λ)→(PK, sk)): 一个PPT 算法, 其输入为安全参数λ和系统参数params, 输出用户的公钥PK 和私钥sk.
• 可链接环签名生成(LRSign(M,n,S,skπ)→(σ,Qπ)): 一个PPT 算法, 其输入为消息M、n个成员组成的公钥集合S={PK1,PK2,··· ,PKn}以及签名者私钥skπ(1≤π ≤n), 输出签名值σ和链接标签Qπ.
• 可链接环签名验证(LRVerify(params,M,S,σ,Qπ)→accept/reject): 一个多项式时间的确定性算法, 其输入为系统参数params、签名消息M、环成员公钥集合S、签名值σ和链接标签Qπ, 若(σ,Qπ) 是关于M的有效签名, 则输出accept; 否则, 输出reject.
• 链接算法(Link(S,M1,M2,σ1,Q1,σ2,Q2)→linked/unlinked: 一个确定性算法, 输入用户公钥集合S、两个不同的签名消息M1,M2及其分别对应的可链接环签名(σ1,Q1),(σ2,Q2), 若σ1,σ2是有效的环签名且有相同的链接标签Q1=Q2, 输出linked, 否则输出unlinked.一个安全的环签名方案需要满足以下3 个性质:
• 正确性: 由“环签名生成” 算法输出的签名值作为“环签名验证” 算法的输入, 总是输出accept.环签名方案的不可伪造性和无条件匿名性通过模拟器S和敌手A之间的游戏定义, 下面首先介绍A可查询的谕言机JO、CO、SO.
– 加入谕言机(JO(⊥)→PK): 通过此查询, 一个新用户被添加到系统并输出新用户的公钥PK.
– 腐化谕言机(CO(PKi)→ski): 输入用户的公钥PKi, 输出对应的私钥ski.
– 签名谕言机 (SO(M,n,S,PKπ)→ σ): 输入签名消息M, 大小为n的公钥集合S={PK1,PK2,··· ,PKn}, 签名者公钥PKπ(1≤n ≤π), 返回有效的环签名σ.
Pointcheval 等人最早基于“谕言重放攻击” 技术的分叉引理给出了数字签名方案的安全性证明[39], 谕言重放攻击是通过重放敌手一个有效的攻击实现, 该敌手是一个概率多项式时间的图灵机, 能够使用不同的随机谕言机获得关于同一个消息m的两个签名(δ0,h0,σ0) 和(δ1,h1,δ1),其中σ0,σ1分别是攻击者通查询环签名生成谕言机输出的两个签名值, (δ0,h0),(δ1,h1) 分别是计算两个签名值过程中的中间值,h0,h1为随机谕言机的输出, 且有δ0=δ1,h ̸=h′. 根据上述两个签名就可以得到一个困难问题的解.
在一般环签名(generic ring signature) 的定义下, Herranz 等人使用基于“谕言重放攻击” 技术的分叉引理证明了环签名方案的不可伪造性[40]. 一般环签名的定义如下:
定义3 (一般环签名) 一般环签名的定义与本文所定义的环签名都包含4 个基本算法: 系统初始化算法、密钥生成算法、环签名生成以及环签名验证. 关键之处在于一般环签名对签名值的生成过程提出了更具体的要求: 输入消息M、n个成员的公钥(A1,A2,··· ,An)、签名者私钥skπ(1≤π ≤n) 以及安全的哈希函数, 通过产生一组r1,r2,··· ,rn,h1,h2,··· ,hn, 最终输出签名值σ. 其中ri ̸=rj,i ̸=j,hi(1≤i ≤n) 是由m,ri(1≤i ≤n) 以及环成员的公钥确定的哈希值,签名值σ完全由r1,r2,··· ,rn,h1,h2,··· ,hn和消息m决定.
下面给出在一般环签名的定义下不可伪造性的概念.
• 不可伪造性: 环签名的不可伪造性通过模拟器S和敌手A之间的下述游戏定义:
–S生成系统参数params 并将其发送给A;
–A适应性查询谕言机JO、CO、SO 以及随机谕言机H;(2)S∗中所有的公钥均通过查询加入谕言机JO 得到;

(3)S∗中所有的公钥都没有被腐化查询, 即敌手没有得到S∗中任意环成员的私钥;
(4)σ∗不是通过查询签名谕言机SO 得到.如果对任意PPT 的敌手A来说, 赢得上述游戏的概率是可忽略的, 则称环签名方案是不可伪造的.
• 无条件匿名性: 环签名方案的无条件匿名性通过模拟器S和有无限计算力的敌手A之间的游戏
定义:
–S生成系统参数params 并将其发送给A.

–A可适应性查询加入谕言机JO.的基数, 则称环签名满足无条件匿名性.可链接环签名不仅满足上述正确性、不可伪造性和无条件匿名性, 还需要具备可链接性和不可诽谤性.
• 链接性: 链接性是可链接环签名的必备性质, 即一个签名者不能生成两个有不同链接标签的签名值. 链接性通过模拟器S和敌手A之间的下述游戏定义:
–S生成系统参数params 并将其发送给A;
–A可适应性查询谕言机JO、CO、SO;
–A输出两组可链接环签名值(S,M1,σ1,Q1) 和(S,m2,σ2,Q2).称A赢得了上述游戏如果满足以下4 个条件:
(1) 集合S中的公钥均是通过查询加入谕言机JO 得到;
(2)A向腐化谕言机CO 查询S中公钥对应的私钥不超过两次, 即敌手A最多获取S中一个用户的私钥;
(3) (σ1,Q1),(σ2,Q2) 分别是关于消息M1,M2的有效环签名, 即LRVerify(M1,S,σ1,Q1)→accept, LRVerify(M2,S,σ2,Q2)→accept, 并且σ1,σ2不是签名谕言机SO 的输出值;
(4) Link(S,M1,M2,σ1,σ2)→unlinked.
如果对任意PPT 的敌手A来说, 赢得上述游戏的概率是可忽略的, 则称可链接环签名满足链接性.
• 不可诽谤性: 不可诽谤性指敌手A不能生成与真实签名者签名相同的签名标签, 这一性质保证了
A不能陷害真实签名者. 不可诽谤性通过模拟器S和敌手A之间的下述游戏定义:
–S生成系统参数params 并将其发送给A.
–A可适应性查询加入谕言机JO.
–A将签名消息M,n个用户公钥组成的集合S={PK1,PK2,··· ,PKn}以及随机选择的π ∈{1,2,··· ,n}发送给S, 其中用户π的公钥PKπ没有被腐化查询或没有作为签名查询SO查询中的输入;S使用PKπ对应的私钥skπ执行可链接环签名生成算法LRSign(M,n,S,skπ),最后将生成的签名值{σ,Q}发送给A.
–A适应性查询谕言机JO、CO、SO.
(1) LRVerify(params,M∗,S,σ∗,Q∗)=accept;
(2)σ∗不是签名谕言机SO 的输出;
(3)S∗中的公钥都是加入谕言机JO 的输出;
(4) PKπ没有被敌手腐化查询;
(5) Link(S,M,M∗,σ,Q,σ∗,Q∗)→linked.
如果对任意PPT 的敌手A来说, 赢得上述游戏的概率是可忽略的, 则称可链接环签名方案满足不可诽谤性.
本小节最后给出椭圆曲线上的离散对数问题.
椭圆曲线离散对数问题(ECDLP): 给定椭圆曲线E(Fp) 上任意两点P,Q, 求解满足等式Q=x·P的值x是多项式时间内不可解的.
2.2 SM2 数字签名算法
本节介绍SM2 数字签名算法的4 个阶段: 系统参数生成、密钥生成、签名和验证.
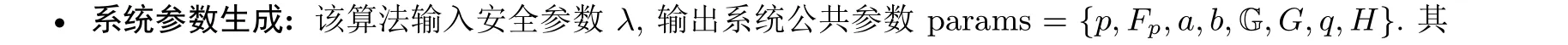

3 基于SM2 数字签名算法的环签名方案
3.1 SM2 环签名方案
环签名方案因其“环签名生成算法” 生成的某些值按一定规则构成一个环状而得名, 本文以Rivest 等人提出的环签名概念为基准, 基于SM2 数字签名算法设计了一个安全的环签名方案, 下面给出SM2 环签名方案的4 个算法.


算法1 SM2 环签名生成算法Input: m,L = {P1,P2,··· ,Pn},dπ Output: 环签名σL(m) = (c1,s1,s2,··· ,sn)1 产生随机数kπ ∈Z∗q, 计算cπ+1 = H1(L,m,kπ ·G);2 对i = π+1,··· ,n,1,··· ,π −1,, 依次执行以下运算:3 随机产生si ∈Z∗q, 计算Zi = si·G+(si+ci)·Pi,ci+1 = H1(L,m,Zi), 其中记c1 = cn+1;4 计算sπ = ((1+dπ)−1 ·(kπ −cπ ·dπ)) mod q;5 输出在L 上关于m 的环签名(c1,s1,s2,··· ,sn).

3.2 SM2 可链接环签名
本节在SM2 环签名方案的基础上, 通过嵌入安全的签名标签, 设计了基于SM2 数字签名算法的可链接环签名方案极其两种变型方案, 下面介绍SM2 可链接环签名方案的5 个算法: 系统初始化算法、密钥生成算法、可链接环签名生成、可链接环签名验证和链接算法.
• 系统初始化算法: 该算法输入安全参数λ,输出系统参数params={p,Fp,E(Fp),G,G,q,H1,Hp},其中p是大素数,E(Fp) 是定义在有限域Fp上的椭圆曲线, G 表示椭圆曲线上的点构成的加法循环群,G是循环群G 的生成元, 阶为素数q,H1:{0,1}∗→Z∗q,Hp:{0,1}∗→G 是两个安全的哈希函数.
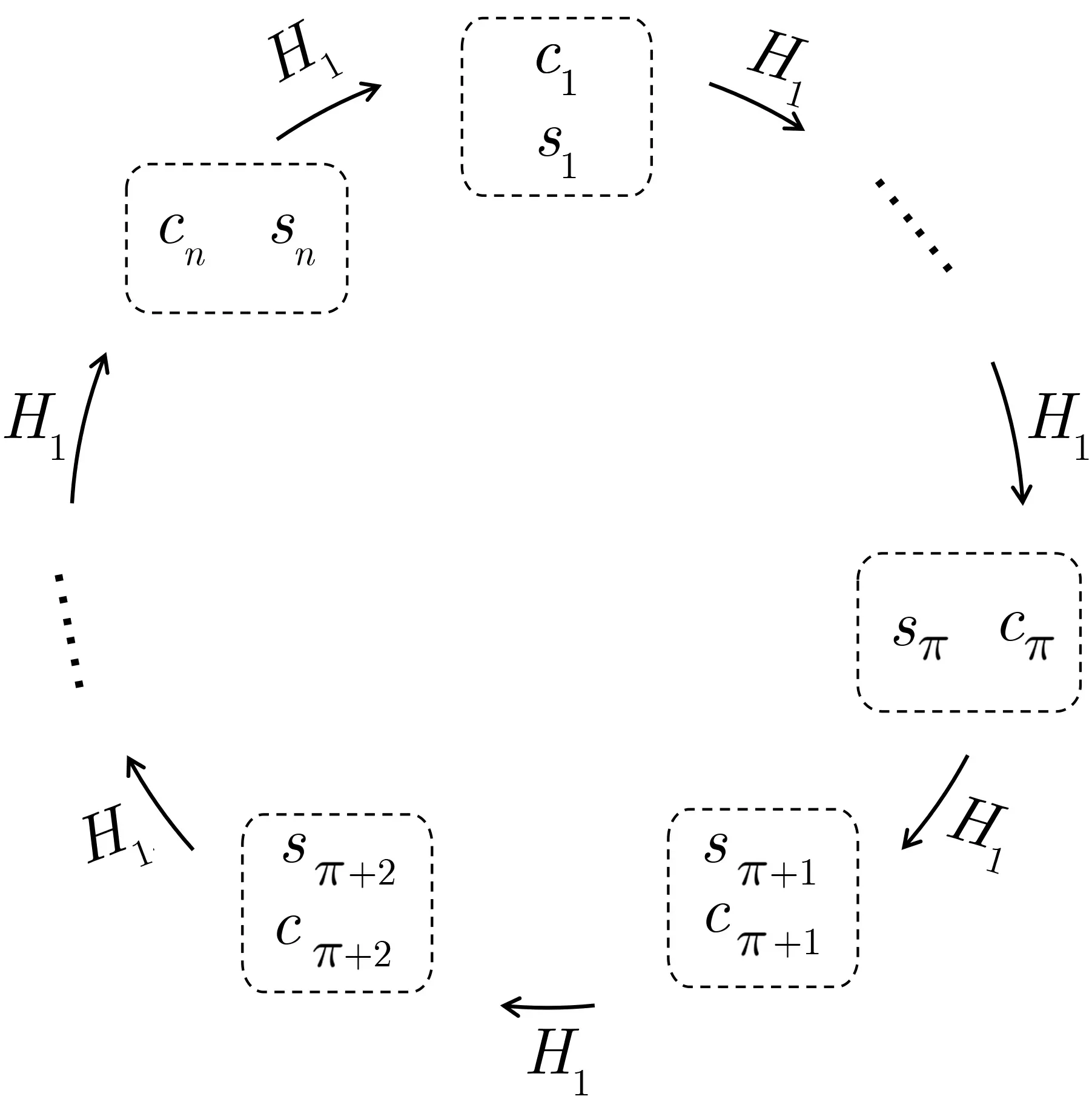
图1 环结构Figure 1 Ring structure
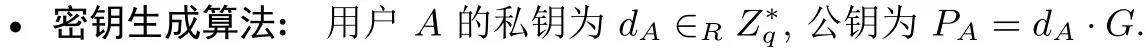
• 可链接环签名生成: 签名者任意选取n−1 个用户公钥,加上自身公钥构成群组L={P1,P2,··· ,Pn}; 签名者为其中第π(1≤π ≤r) 个用户, 利用私钥dπ和环成员公钥L生成对消息m的可链接环签名, 如算法2:

算法2 SM2 可链接环签名生成算法Input: m,L = {P1,P2,··· ,Pn},dπ Output: 可链接环签名σL(m) = (Qπ,c1,s1,s2,··· ,sn)1 计算签名标签Qπ: R = Hp(L),Qπ = dπ ·R;2 随机选取kπ ∈Z∗q, 计算cπ+1 = H1(L,Qπ,m,kπ ·G,kπ ·R);3 对i = π+1,··· ,n,1,··· ,π −1, 随机产生si ∈Z∗q, 并依次计算Vi = si·G+(si+ci)·Pi,Wi = si·R+(si+ci)·Qπ,ci+1 = H1(L,Qπ,m,Vi,Wi), 其中记c1 = cn+1;4 计算sπ = ((1+dπ)−1 ·(kπ −cπ ·dπ)) mod q;5 输出可链接环签名(Qπ,c1,s1,s2,··· ,sn).
• 可链接环签名验证: 为了检验收到的消息m′及其可链接环签名(c′1,s′1,s′2,··· ,s′n,Q′π), 验证者实现以下步骤:
– 计算R=Hp(L);

下面给出SM2 可链接环签名方案的两种变型.



算法3 SM2 可链接环签名变型一Input: m,L = {P1,P2,··· ,Pn},dπ Output: 可链接环签名σL(m) = (Qπ,c1,s1,s2,··· ,sn)1 计算签名标签Qπ: R = Hp(L),Qπ = dπ ·R;2 随机选取kπ ∈Z∗q, 计算cπ+1 = H1(L,Qπ,m,kπ ·(G+R));3 对i = π+1,··· ,n,1,··· ,π −1, 随机产生si ∈Z∗q, 并依次计算Zi = (si +ci)·(Pi +Qπ)+si ·(G+R),4 ci+1 = H1(L,Qπ,m,Zi), 其中记c1 = cn+1;5 计算sπ = ((1+dπ)−1 ·(kπ −cπ ·dπ)) mod q;6 输出可链接环签名(Qπ,c1,s1,s2,··· ,sn).
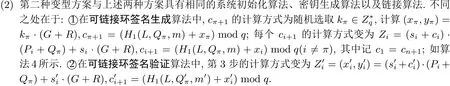

算法4 SM2 可链接环签名变型二Input: m,L = {P1,P2,··· ,Pn},dπ Output: 可链接环签名σL(m) = (Qπ,c1,s1,s2,··· ,sn)1 计算签名标签Qπ: R = Hp(L),Qπ = dπ ·R;2 随机选取kπ ∈Z∗q, 计算(xπ,yπ) = kπ ·(G+R),cπ+1 = (H1(L,Qπ,m)+xπ) mod q;3 对i = π+1,··· ,n,1,··· ,π −1, 随机产生si ∈Z∗q, 并依次计算Zi = (xi,yi) = (si +ci)·(Pi +Qπ)+si ·(G+R),4 ci+1 = (H1(L,Qπ,m)+xi) mod q, 其中记c1 = cn+1;5 计算sπ = ((1+dπ)−1 ·(kπ −cπ ·dπ)) mod q;6 输出可链接环签名(Qπ,c1,s1,s2,··· ,sn).
4 安全性分析
本节主要证明SM2 (可链接) 环签名方案的正确性、不可伪造性、无条件匿名性以及SM2 可链接环签名方案的链接性、不可诽谤性.
定理1 SM2 环签名方案满足正确性.
证明: 假定签名σL(m) = (c1,s1,s2,··· ,sn) 按照算法1 产生, 验证者根据环签名验证算法进行验证, 则有:
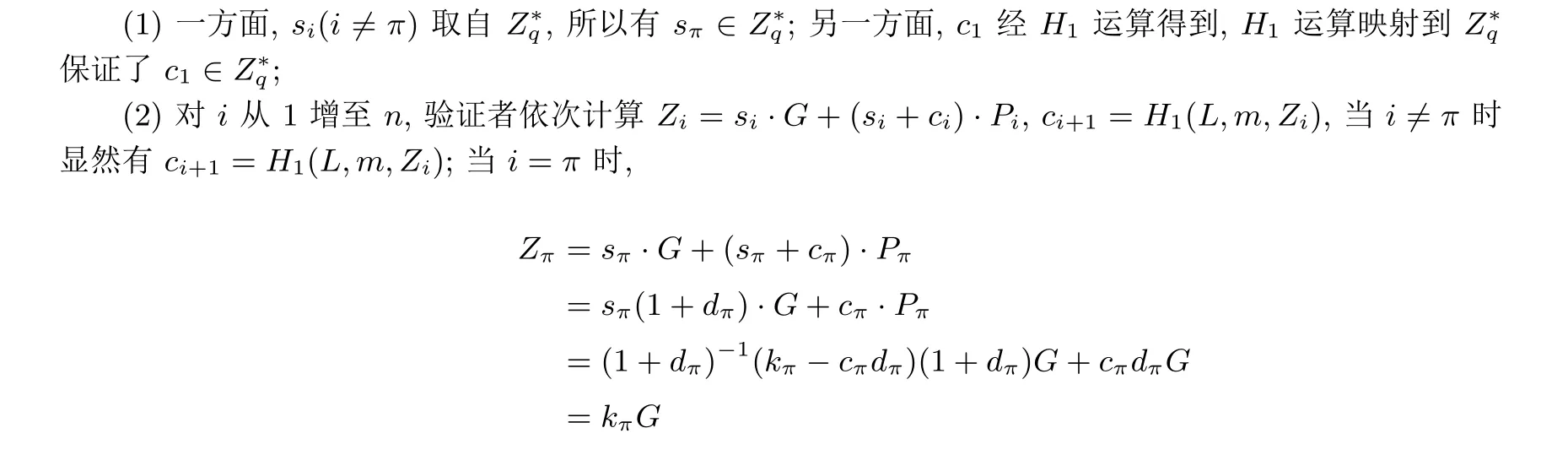
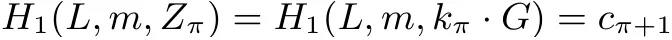
因此满足c1=cn+1, 正确性得证.
为了证明本文中的方案在随机谕言模型下抵抗适应性选择消息攻击, 首先分析本文的方案满足一般环签名的概念, 然后证明在椭圆曲线离散对数问题困难的假设下, 本文提出的方案满足不可伪造性.
分析: 在SM2 环签名方案中,算法1 展示了签名值的生成过程: 输入为消息m、公钥L={P1,P2,···,Pn}、私钥skπ以及哈希函数H1, 中间值为(Z1,Z2,··· ,Zn,c1,c2,··· ,cn), 输出的签名值为σ=(c1,s1,s2,··· ,sn). 其中,ci+1=H1(L,m,Zi) 显然是由L,m,Zi确定的哈希值, 从而SM2 环签名是文献[40] 定义的一般环签名的一个实例, 因此分叉引理适用. 同理可分析SM2 可链接环签名方案也满足一般环签名的定义. 下面主要介绍SM2 环签名方案的不可伪造性.
定理2 若椭圆曲线离散对数问题(DLP) 是困难的, 则SM2 环签名具有不可伪造性.

(G,Q) 问题可解, 与假设矛盾, 定理得证.
定理3 SM2 环签名方案满足无条件匿名性.


可链接环签名方案的正确性、不可伪造性、无条件匿名性证明过程与环签名方案相似, 下面主要证明SM2 可链接环签名的可链接性和不可诽谤性.
定理4 假设离散对数问题(DLP) 是困难的, 则在随机谕言机模型下SM2 可链接环签名具有链接性.

定理5 SM2 可链接环签名满足不可诽谤性.

5 效率分析
5.1 通信量

5.2 计算量
本节分别统计SM2 环签名方案和SM2 可链接环签名方案的计算量与环成员数量的关系, 如表1 所示.

表1 SM2 环签名方案的计算量Table 1 Computation quantity for SM2 ring signature schemes
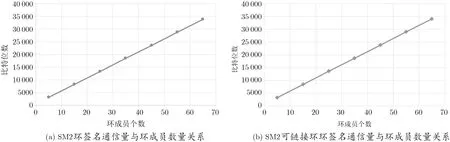
图2 通信量与环成员数量关系Figure 2 Relationship between communication cost and number of ring members
针对SM2 环签名方案, 假设环成员数量为n, 以循环群G 上的点乘、点加、H1运算以及Zq上逆运算的计算量统计计算复杂度. SM2 环签名过程中, 生成cπ+1时包含一次G 上点乘运算、一次H1运算,生成与其他n −1 个ci(1≤i ≤n,i ̸=n) 时包含2n −2 次G 上点乘、n −1 次G 上点加和n −1 次H1运算, 最后生成sπ时包含一次Zq上逆运算; 验证过程包含n次G 上点加、2n次G 上点乘和n次H1运算.
针对SM2 可链接环签名方案, 假设环成员数量为n, 以循环群G 上的点乘、点加、H1运算以及Zq上逆运算的计算量统计计算复杂度.SM2 可链接环签名生成过程中, 首先计算链接标签Qπ需要1 次Hp运算、1 次G 上点乘运算; 然后计算cπ+1包含2 次点乘运算、1 次H1运算, 计算其他n −1 个ci(1≤i ≤n,i ̸=n) 时总共包含4n −4 次点乘、2n −2 次点加和n −1 次H1运算, 最后生成sπ时包含一次Zq上的逆运算; 可链接环签名验证过程包含1 次Hp运算、4n次G 上点乘、2n次点加和n次H1运算.
6 结束语
环签名是一种特殊的数字签名, 它允许一个成员代表一组人进行签名而不泄漏签名者的信息, 实现了签名的无条件匿名性, 可以保护用户的隐私; 可链接环签名是一种具有签名人关联性的环签名, 实现了签名的无条件匿名性和可链接性, 即保护用户隐私的同时保证了签名的可链接性. 环签名/可链接环签名在电子投票、数字货币等多个领域有着广泛应用. 科研人员已经提出了多种不同形式和不同特性的环签名算法, 但没有基于SM2 数字签名算法的环签名. 为了推广SM2 数字签名算法在这些领域的应用, 本文提出了基于SM2 数字签名算法的环签名/可链接环签名, 并证明了其安全性, 具有安全性高、实现简单、易验证的特点. 下一步的工作重点是减弱环签名通信量、计算量与环成员数量的关系, 如对数关系甚至与环成员数量无关.

