ODBR-DCSK系统调制技术研究

张 桐，隋 涛，虞明灯，蒋 强

(1.沈阳理工大学 a.信息科学与工程学院；b.自动化与电气工程学院，沈阳110159；2.中国人民解放军63612部队，甘肃 敦煌 736200)

正交混沌信号具有良好的宽频谱特性、非周期性和对初始条件的极度敏感性，因此被广泛应用于数字通信和扩频通信中[1-2]。混沌数字调制技术是用混沌信号取代传统正弦载波，既完成信息调制也实现频谱扩展，保留了扩频通信的优势，还可实现保密通信，且电路实现简单，具有广阔的应用前景和实用价值[3-7]。在诸多的非相干混沌数字调制技术中，差分混沌移位键控(Differential Chaos Shift Keying，DCSK)技术因其可靠性高而得到各国学者的青睐[8-9]，但其存在传输速率较低的问题。文献[10]针对DCSK传输速率较低的缺点提出了双倍速差分混沌移位键控(Double Bit Rate Differential Chaos Shift Keying，DBR-DCSK)通信方案，比特传输速率得到了很大改善，但该方案解调时需要定时同步。

针对DCSK算法存在传输速率低的缺陷，本文提出正交双倍速差分混沌移位键控(Orthogonal Double Bit Rate Differential Chaos Shift Keying，ODBR-DCSK)算法，对系统的误码性能进行仿真分析，探究混沌映射种类、半扩频因子β等对ODBR-DCSK系统的误码性能影响；研究在相同条件下ODBR-DCSK系统与DCSK系统的性能差异。

1 ODBR-DCSK系统原理

1.1 发送端

与DCSK系统的信号结构相似，ODBR-DCSK系统仍采用传输参考模式，在ODBR-DCSK系统中每个码元同样被划分为前后两个相等的时隙，在前一个时隙内传输长度为β的经混沌映射系统产生的混沌信号，称为参考时隙；在后一个时隙中，传输2比特经不同的混沌信号调制的数据信号，称为信息时隙。

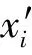
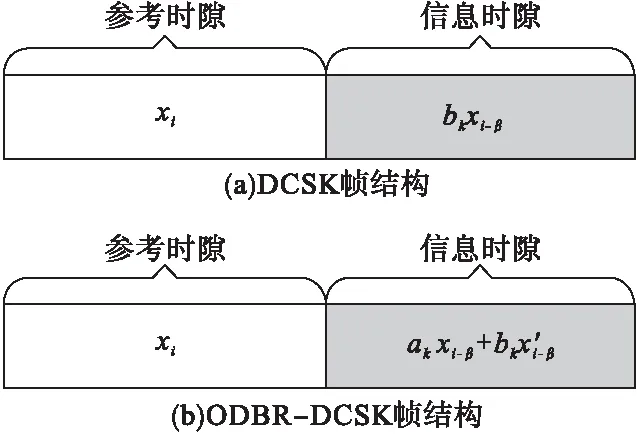
图1 ODBR-DCSK系统与DCSK系统帧结构

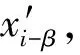
图2 ODBR-DCSK系统调制结构

依据上述描述，结合图2，该系统在第k个符号周期内所传输信息Si的表达式为

(1)

1.2 接收端

图3为ODBR-DCSK系统解调器结构图。

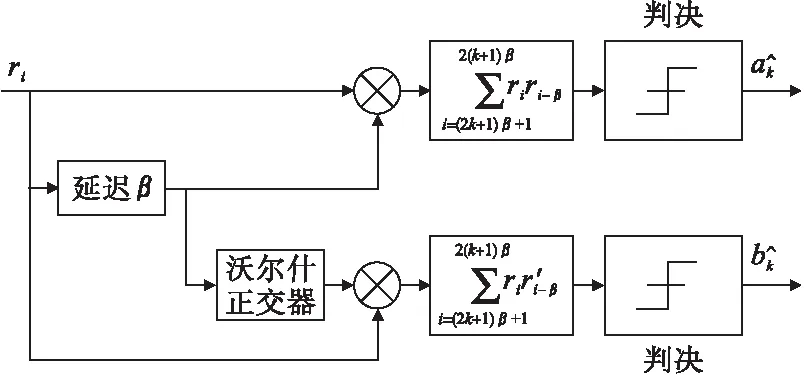
图3 ODBR-DCSK系统解调器结构

由图3可知，在第k个码元周期内，系统恢复信息时，先将接收到的信号与自身延迟半个周期后的信号进行对应位置的相乘；然后将半个周期内的信号值进行累加；最后将累加的信号值与判决门限值进行比较。ak只对其中一路信号进行恢复；对于bk信号的恢复，需要将接收到的参考信号进行与接收端同样的沃尔什正交处理，然后将正交处理后的混沌参考信号和信息信号相乘相加，将结果与判决门限值比较，得出原始信号。

2 ODBR-DCSK性能分析

2.1 系统能量利用率分析

将一个码元周期内的参考时隙和信息时隙的能量分别用Eref和Edata表示，用Eb-DCSK表示DCSK系统发射时的比特能量，公式为

(2)

在ODBR-DCSK系统中，一个码元周期内发送的比特能量可以表示为

(3)

由于两组混沌信号是通过沃尔什函数产生的在一个周期内统计有半周期混沌信号互为相反数；由于特殊的正交关系，公式(4)的第二项为0，故在一个码元周期内信号的比特能量为

(4)

DCSK系统和ODBR-DCSK系统在一个码元周期内信号的能量相等。两个系统对比可知，要发送相同数量的数据，DCSK系统所需要的能量是ODBR-DCSK系统的两倍，因此ODBR-DCSK系统的能量利用率相比DCSK系统提高了一倍。

2.2 高斯白噪声信道下误码率分析

假设在高斯白噪声信道下的信道系数在每个符号周期内保持不变(为常数1)，同时假设在该信道中只含有一种加性高斯白噪声，则通过高斯白噪声信道后，接收机接收到的信号为ri，满足ri=si+ni，其中ni为服从高斯分布的白噪声，其均值为0，方差为N0/2。

根据图3的解调器结构图，可将判决信号Z1、Z2表示为

(5)

(6)

(7)

(8)

假设数据源是等概率的发送二进制信息{1，-1}，信息码元ak的BER表达式为

(9)

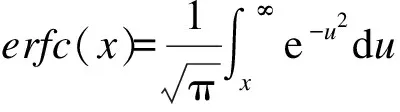
将式(7)、式(8)带入式(9)中，可得到ODBR-DCSK系统的BER表达式为

(10)

对于判决变量Z2的计算也采用高斯近似法，与Z1计算结果相同。记信息码元ak的误码率为BER1，信息码元bk的误码率为BER2，满足BER1=BER2。因此，ODBR-DCSK系统在AWGN信道条件下的平均BER表达式为

(11)

在高斯白噪声信道下，ODBR-DCSK方案理论误码率和实验BER关系曲线如图4所示。由图4可以看出，实验BER和理论BER基本吻合。

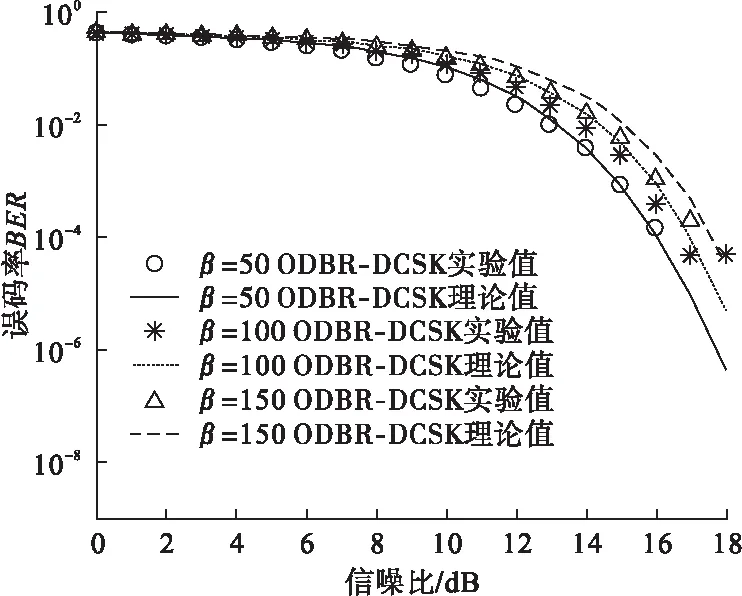
图4 ODBR-DCSK实验误码率和理论误码率的比较

3 仿真分析

3.1 半扩频因子β对BER的影响

图5为ODBR-DCSK系统在β分别为50、100、150情况下BER随信噪比变化曲线。

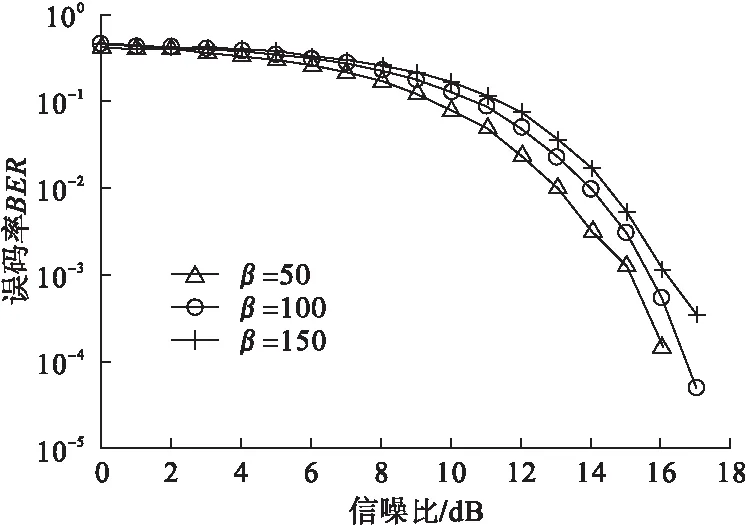
图5 不同β下BER随信噪比变化曲线

由图5可知，选择不同的β会对系统产生不同的影响。对于改进型Logistic混沌映射来说，选择的β较小时，误码率BER较小；随着β的增大，系统的误码率BER也随之增大。

图6是在信噪比为13dB和15dB的情况下，ODBR-DCSK系统BER随β变化的曲线。

图6 不同信噪比下BER与β的关系

由图6可以看出，随β的增加，误码性能呈现先变好后变坏的趋势；在不同信噪比下，同一混沌映射对于ODBR-DCSK系统要取得较好的误码性能，半扩频因子的最佳取值也略有不同。

3.2 不同系统间比较

图7为 DCSK系统和ODBR-DCSK系统在相同条件下BER的关系对比图。

图7 DCSK与ODBR-DCSK同条件下BER比较

采用初值为0.35的改进型Logistic映射，半扩频因子β分别为18、50和100时的实验结果表明，在相同条件下DCSK系统的误码性能优于ODBR-DCSK系统。

4 结论

针对DCSK系统传输速率慢的缺点进行了改进，提出了ODBR-DCSK系统。实验结果表明：ODBR-DCSK系统整体呈现随半扩频因子的增大，误码性能出现先改善后恶化的现象；ODBR-DCSK系统相比DCSK系统具有更高的传输速率。