SSA和DSC-ResNet的TE过程故障诊断方法

付丽君，张齐鹏，姜宇宏，杨 青

(沈阳理工大学 自动化与电气工程学院，沈阳 110159)

近年来，随着现代化工业过程的大规模生产与发展，使得化工过程的操作复杂性不断增加，操作设备出现老化和腐蚀的情况日益增多，由此可能出现化学物质泄露、火灾、爆炸等难以预测的安全隐患的发生，同时也会导致环境污染等严重的人身安全问题和财产损失事故[1]。因此，对化工过程进行故障诊断可以预防灾难性事故的发生和减少人员的伤亡以及达到保证产品质量的目的。

伊斯曼化学公司创建的田纳西-伊斯曼(TE)化工过程，其主要作用是对化工过程的故障诊断及监测研究领域提供实际的工业过程控制数据集。现阶段，使用TE数据集进行故障检测和诊断的研究已经取得了一定的进展和成果；并且由于研究者对深度学习和神经网络研究的不断深入，使得更多的研究者以深度学习和神经网络为基础，对TE过程进行故障诊断分析。

刘丽云等[2]使用K-means聚类方法对TE过程进行故障诊断，并通过主成分分析(Principal Component Analysis，PCA)方法对故障发生的原因进行分析和识别。Wu D S等[3]提出了基于提升小波和支持向量机(Lifting Wavelets and Support Vector Machine，LWSVM)相结合的故障诊断方法；首先使用提升小波对数据集进行预处理操作，然后使用支持向量机(Support Vector Machine，SVM)进行故障诊断。杨青等[4]提出一种基于变分模态分解、独立主成分分析和核主成分分析相结合的多模态故障检测方法，以此达到对TE过程进行故障诊断的目的。Gu X H等[5]提出一种基于混合卷积神经网络的结构模型，对TE过程进行故障诊断；同时这一模型在卷积神经网络中加入Mixup卷积网络，以此训练网络模型，获得更好的泛化能力。付丽君等[6]提出了基于图像的轻量级卷积神经网络对轴承故障数据进行诊断的方法，针对轴承故障数据通过小波包变换的方式将一维数据转化成二维图像数据，然后通过分类网络对二维图像数据进行故障诊断。

综上，在针对TE数据的诊断分类上，大多数方法是对一维数据直接进行处理并分类。但相比于一维数据，二维图像数据更易通过卷积神经网络来进行特征提取，从而保证数据特征的全面性及分类的准确性。所以本文采用小波包变换的方法对TE数据进行处理，生成二维小波图像；然后通过改进残差网络模型对预处理后的TE数据进行特征提取并完成相应的故障诊断分类。相比较于其他一维数据的处理方式，本文采用的预处理生成图像数据的方法可以更大程度保留和提取原始信号的特征，达到进一步提高TE化工过程故障诊断精度的目的。

1 WPT-SSA-ResNet方法

1.1 小波包图像生成

小波变换[7]是一种新型的关于线性时频分析的方法。所谓的“小波”是指其本身具备的衰减性和波动性，其主要作用是自动适应时频信号的分析要求。小波变换对原函数使用小波从不同的角度对函数进行分解，通过这种方式得到原函数在不同尺度小波下的系数。而小波包变换(Wavelet Packet Transform，WPT)[8]可以理解为是小波变换的一种升级和优化，其与小波变换最大的区别在于：小波变换是对低频部分进行分解，将其分解为高频、低频两类；而小波包变换则是对高、低频两部分进行分解。可以将小波包变换看作信号在子空间坐标系下的投影。第j层分解后的小波包节点可表达为

(1)

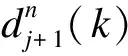
通过上述方式生成的二维TE图像数据如图1所示。

图1 经小波包处理后的图像数据

本文对TE数据进行二维图像的转换时，利用小波包变换对每一个输入的信号进行第10层分解，即j=10，并对节点能量进行计算。从上至下、从左至右对应小波包图像的每个像素点，构成小波包图像的能量矩阵为

(2)

式中q表示生成小波包图像的维度。

1.2 麻雀搜索算法(SSA)

受到麻雀生物群体社会性的启发及人工智能的发展需要，Xue J K等[9]在2020年提出了一种用于处理优化问题的新型优化算法——麻雀搜索算法(Sparrow Search Algorithm，SSA)。SSA算法中将n只麻雀组成的种群用公式表达为

(3)

式中：d为待优化问题的变量维数；n为麻雀的数量；X为种群。所以麻雀的适应度值可以表达为

(4)

式中Fx表示适应度函数值，在该算法中分为发现者和加入者两大类，较好适应度值的发现者能够优先获取食物，同时，作为发现者还负责整个种群的食物寻找及为加入者提供食物方向。

1.3 深度可分离卷积

深度可分离卷积与原始的卷积操作不同。深度可分离卷积使用通道数为1的卷积核对输入的特征层进行逐层的特征提取，然后再使用1×1的卷积核对融合后的输出特征层的通道数进行调节[10]。将深度可分离卷积的思想应用到残差分类网络中，构成深度可分离卷积残差网络(Dept-hwise Sparable Convolution-ResNet，DSC-ResNet)模型，该模型改变残差网络中传统的卷积操作，从而减少了模型的参数，改变了计算方式，并缩短了训练时间。深度可分离卷积的示意图如图2所示。

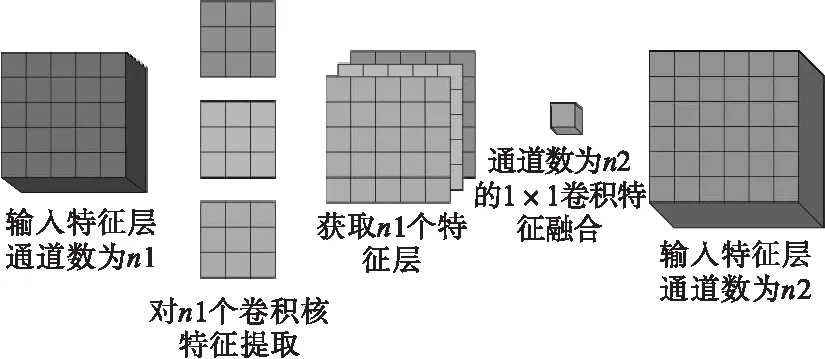
图2 深度可分离卷积示意图

在卷积核为3×3、输入特征层的通道为3、输出特征层参数为16的情况下，分别进行一次卷积操作和深度可分离卷积操作。计算通过卷积操作后的参数量为3×3×3×16=432，而进行深度可分离卷积操作后的参数量为3×3×3+3×1×1×16=75。可以明显看出，进行深度可分离卷积操作和进行卷积操作的计算方式不同，从而减少了参数量，达到降低训练时间复杂性的目的。

1.4 WPTS-SAA-DSC-ResNet算法

该算法主要分为数据预处理阶段和故障分类阶段。WPTS-SAA-DSC-ResNet算法流程如图3所示。

图3 WPT-SSA-DSC-ResNet算法结构图

预处理阶段第一步，为保证数据的时间连续性，对数据按时间性进行分割；预处理阶段第二步，利用WPT方法将一维时间序列数据转化成为二维图像数据。

故障诊断网络以传统的残差分类网络为基础，但因为传统的残差网络在图像分类应用中，通常使用较多的网络层数以提高对图像分类的精度，因此随着网络层数的不断增多，过多的网络层数也会使网络中的参数数量增加。所以将深度可分离卷积替换到网络中。

故障诊断阶段在对二维图像进行训练诊断时，对网络中的卷积层和深度可分离卷积层进行批量归一化；同时采用SSA智能优化算法对分类网络中的学习率及各个卷积层的大小和数量等主要参数进行优化，以实现在不损失分类精度的基础上缩短分类时间的效果。

2 实验研究

为验证本文的研究方法在TE化工过程中的可行性，采用田纳西-伊斯曼过程作为验证的实验数据集。TE过程主要由反应器、冷凝器、汽提塔等多个单元组成，具体流程如图4所示[11]。

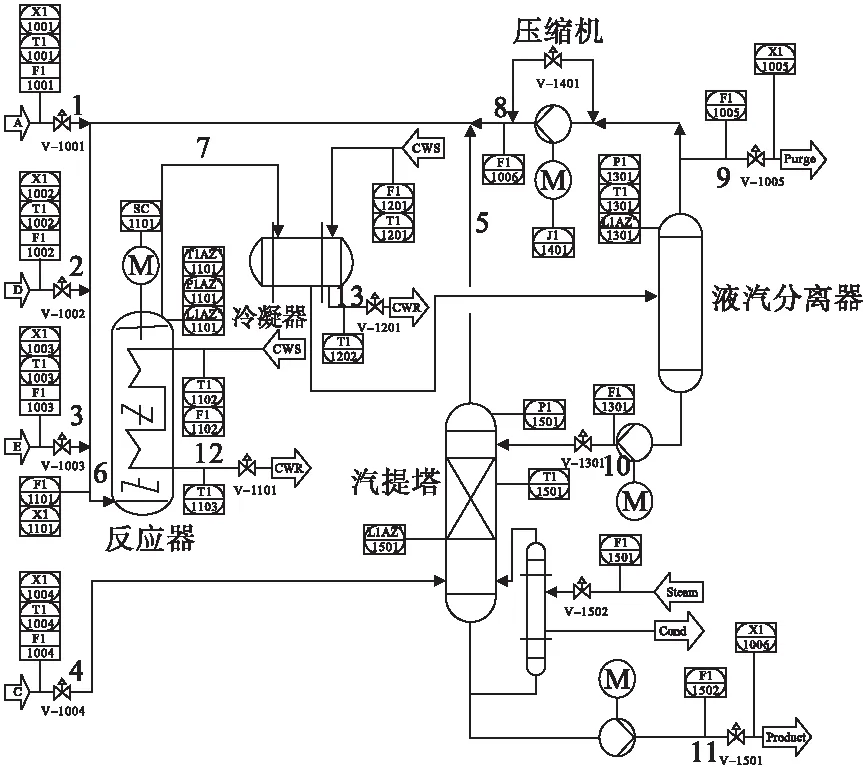
图4 TE过程流程图

在TE过程数据集中对故障进行了如表1所示的定义。本文使用TE过程数据中同一模态下的故障1、故障4、故障8和故障12四种故障数据作为实验的数据集；使用Matlab对数据集进行预处理和图像生成；利用Python软件进行分类网络的实验和验证。在实验过程中，对四种故障数据进行划分，按7∶3的比例将数据集分为训练和测试两个样本，每次训练16张二维图像数据，共迭代20次。图5为二维数据准确率曲线图。

表1 TE过程故障

图5 二维数据准确率曲线图

由图5可知，经过WPT-SSA-DSC-ResNet故障分类网络训练后的训练集的准确率能够达到99%；测试集准确率可达到98%。

损失率的结果如图6所示。由图6可知，利用WPT-SSA-DSC-ResNet故障分类网络训练后，训练集的损失率为0.6%；测试集的损失率为0.2%。

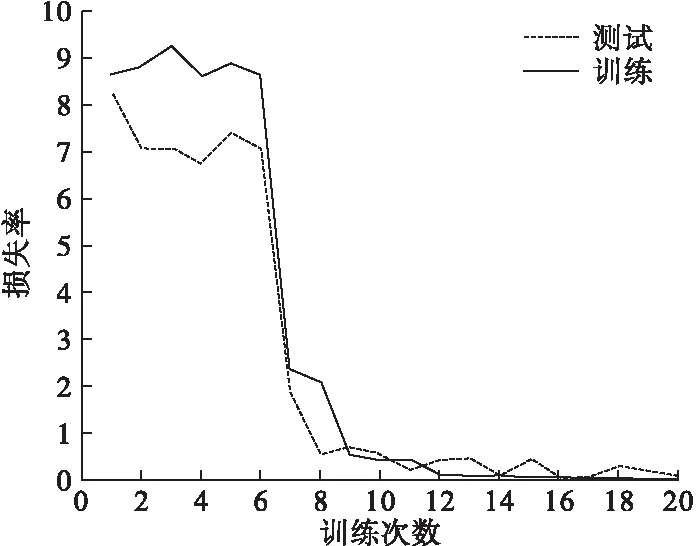
图6 二维数据损失率曲线图

本文提出的故障诊断方法在相同实验数据集下与其他故障诊断方法的准确率对比如表2所示。

表2 故障诊断方法准确率对比 %

通过表2中的数据可知，本文提出的WPT-SSA-DSC-ResNet算法的准确率优于其他模型。

3 结论

针对TE过程提出了一种基于麻雀搜索算法和深度可分离卷积残差网络相结合的集合型故障诊断方法。在数据预处理阶段使用小波包变换对TE数据进行预处理，将其一维数据转换成二维的图像数据；在传统的残差网络基础上将残差网络中的卷积层替换成深度可分离卷积，可有效地减少训练所需时间，提高诊断效率。通过对TE数据分类的实验结果分析，证明了WPT-SSA-DSC-ResNet方法的可行性。