注射模斜顶受力分析

谭宪纲

（深圳市金三维模具有限公司，广东深圳518108）

1 引言

很多塑料制品都会存在出模倒扣结构，这类塑件的注射模通常都会采用滑块抽芯或者斜顶（也叫斜推杆）抽芯机构来解决脱模问题，特别是在塑件内侧出现倒扣时，斜顶机构是最优甚至是唯一的解决方案。斜顶机构除了抽芯的作用外，还兼具顶出作用，占用空间小等优点，所以，这种机构在注射模中应用非常广泛。图1是一个典型的斜顶结构局部构造图。

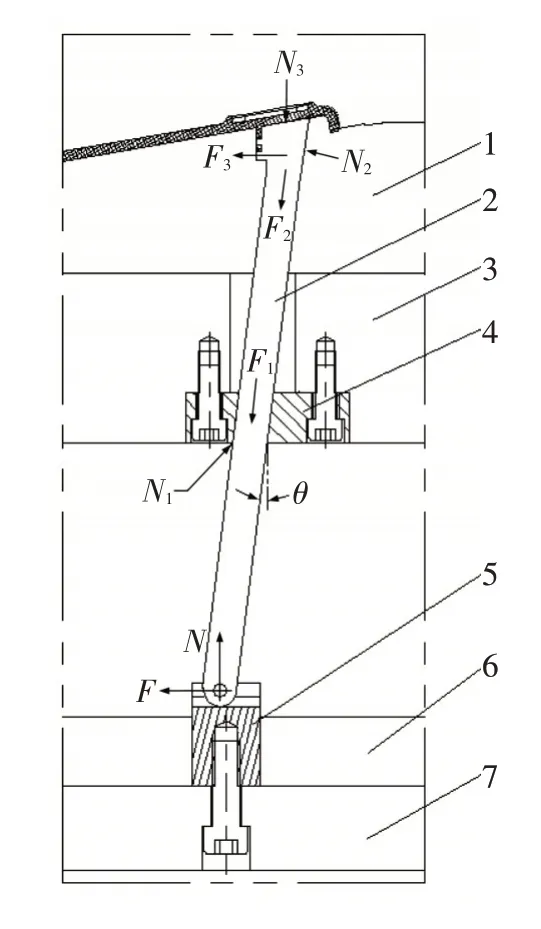
图1 常规斜顶结构图

斜顶机构通常由头部胶位型面及定位、中间导向斜孔及管位、底部斜顶滑座等组成，复杂的还有冷却水路等其它功能部件。而导向斜孔的夹角θ（顶出力方向与运动方向的夹角），会使顶出力产生一个径向的分力，这个径向分力随着θ的加大而变大，并增加斜顶功能失效的风险，如弯曲变形、卡死、折断等。所以夹角θ有一定限制，通常不大于15°~18°，那么这个经验值是否有什么理论依据呢？本文试图通过简化的力学分析来进行探讨。

2 斜顶受力分析

斜顶在运行过程中，主要受力是在顶出和回退（复位）这两个动作过程中产生的，特别是在注射成型后开模顶出启动的瞬间所受的力是最大的，这时候塑件顶出阻力（塑件包紧力）最大，而斜顶机构也正处于由静摩擦向滑动摩擦转换的前夕，摩擦阻力最大，斜顶杆的悬臂也是处于最长位置。所以，这个时候斜顶应该是承受最大破坏力的时机，此时，斜顶的受力如图1所示，N为顶出力，F为底座摩擦力，N1为导向块支撑力，F1为斜顶与导向块的摩擦力，N2为型芯支撑力，F2为斜顶与型芯的摩擦力，N3为塑件顶出阻力，F3为塑件包紧力及摩擦力，θ是斜顶角度。

对于同一副模具上，上述N3和F3基本稳定，可以理解为一个常值，为了方便研究和简化计算，暂不考虑这两个值的影响（相当于未射胶空顶状态），把导向定位部分和型芯部分的支撑力N1、N2简化为两个支点力，并且把斜顶简化为一根长条，这样的简化受力图如图2所示。

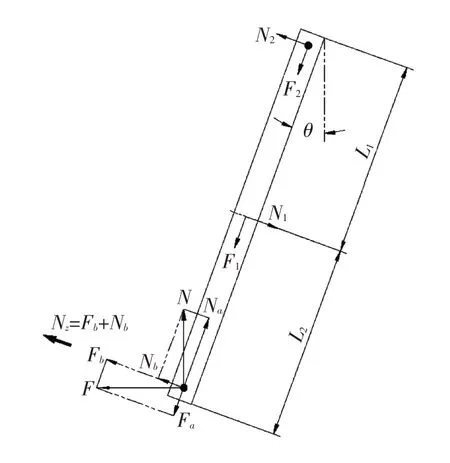
图2 简化斜顶受力分析图（顶出启动瞬间）

图2中，N可以分解为Na（斜顶杆轴向力）、Nb（斜顶杆径向力），F力同样分解为Fa、Fb，由此可得：

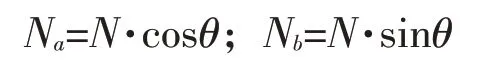
模具和斜顶的材料都是以模具钢为主，它们之间的最大静摩擦系数为μ，则：

F=μN；

Fa=μN·sinθ；Fb=μN·cosθ；

Nb与Fb叠加合力为下端点的径向力Nz：

Nz=Nb+Fb=N·sinθ+μN·cosθ；

图2中，L1相当于模架管位以上部分（藏在模架内），L2相当于管位以下到斜顶座的部分（方铁顶出空间内）。为简化计算且也大致符合常规模具结构尺寸，这里简化设定L1=L2，根据杠杆和力的平衡原理，可得：

N2=Nz；N1=N2+Nz=2Nz

摩擦力F1、F2分别为：

F1=μN1=2μN·sinθ+2μ2N·cosθ

F2=μN2=μN·sinθ+μ2N·cosθ

2.1 斜顶轴向受力分析

斜顶轴向力由顶出分力Na和若干阻力的合力：

动力：Na=N·cosθ

阻力：F1+F2+Fa=4μN·sinθ+3μ2N·cosθ

要推动斜顶，斜顶动作不自锁，要满足动力大于阻力，即：

Na＞F1+F2+Fa

N·cosθ＞4μN·sinθ+3μ2N·cosθ

即斜顶的最大安全顶出角应该是：

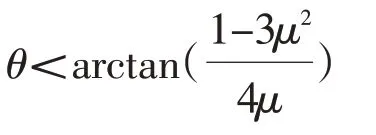
理论上，钢材之间静摩擦系数在0.1~0.15mm，考虑到模具的加工情况及工作环境，实际应该会大于这个理论值。模拟斜顶及斜顶孔的加工工艺及材料，进行摩擦系数的简单验证：

取200×50×50mm的长方形1.2738H材料零件A，其中一个面用慢走丝割出（200×50mm）；取40×40×40mm长方体材料1.2344（46~50HRC）零件B，其中一个面磨削到Ra0.5μm。对应这两个面贴合，按图4所示方法进行简单测试。

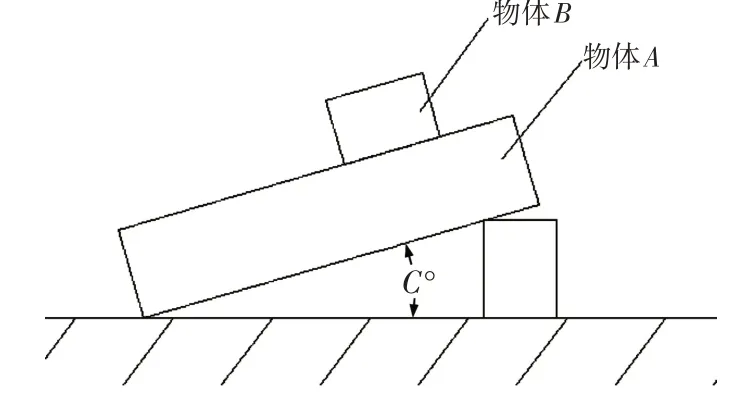
图4 最大静摩擦系数验证方法

多组数据数据试验，B滑动的临界状态，角度C从15°到19°之间，平均约17°，求tan17°≈0.31，得出这两种材料在这种表面状态的摩擦系数μ≈0.31，代入前述轴向受力分析公式，求出：

最大安全角度θ＜30°

民族图腾图案纹样风格。这类风格的纹样基本是以蒙古民族特有的图腾纹样为基础，利用描摹纸将图案描摹到皮上走一遍刀线，然后利用敲边工具，敲打出阴影和立体感。用到的印花工具也是相对比较简单。

考虑到加工精度及装配精度、注射成型中热变形等影响，对摩擦系数取一个1.2倍的安全系数，即取μ=0.37，通过上述计算，可得：θ＜21°。

这个结论与经验值比较接近，特殊情况下，斜顶角做到20°也是有实例的。

从图3可以看出，减少摩擦系数，会显著降增加斜顶的最大安全角度，从而降低斜顶失效的风险。所以，在加工制造中要尽可能提高模具零件表面光洁度、选用合适的材料和表面硬度、提高加工精度和装配精度、改善斜顶的润滑条件等等。

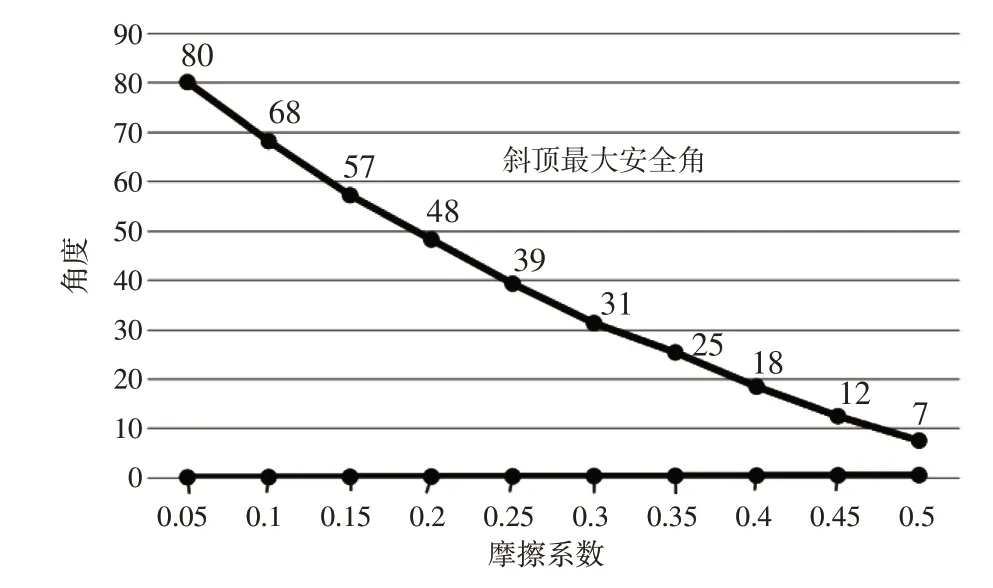
图3 斜顶最大安全角与摩擦系数的关系

2.2 斜顶径向受力分析

从图2简化斜顶受力分析图中看，径向力只有3个，N1、N2和合力Nz。径向没有位移，力学上总体是平衡的。其中L1段有型芯和管位支撑，但L2段是悬臂，在受力情况下会发生变形。把径向力简化为一个悬臂梁结构，如图5所示。

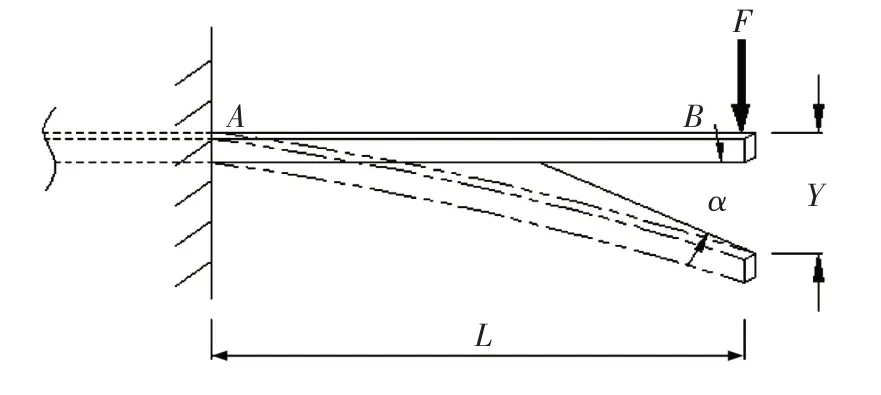
图5 斜顶挠度变形简化

悬臂梁挠度变形计算公式如下：

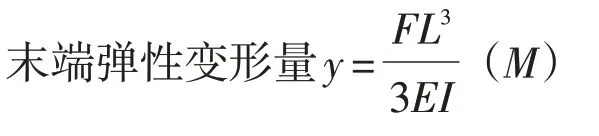
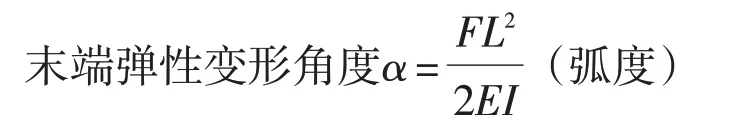
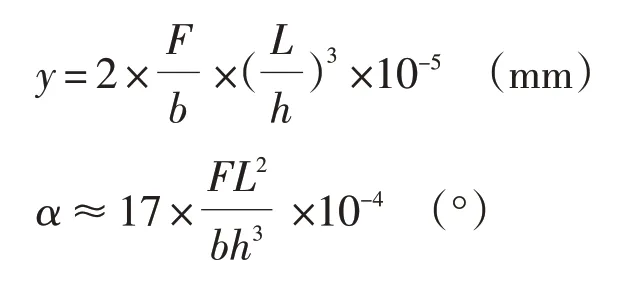
长度单位是毫米，力的单位是牛，角度单位是度。

模拟一个斜顶截面为20×20mm，悬臂长L2=200mm，并且假定合力Nz=200N（约20公斤）的场景，则得：

y=0.2mm α≈0.09°

如果其它条件不变，但斜顶的截面改为20×10mm（h=10），则计算结果是：

y=1.6mm α≈0.64°

从公式和上述计算结果对比可知，斜顶悬臂L和厚度h之比（简称长径比）对变形结果的影响是立方级的，其它因素相对小些。所以，在斜顶设计时尽可能将管位向下（顶杆板方向），以及加大斜顶杆的厚度（或加粗斜顶杆）可以有效的减少变形量。

这种弯曲变形会加大摩擦阻力，导致顶出力加大，从而产生一系列影响，当变形量达到一定程度时会导致斜顶的塑性变形（弯曲）甚至断裂，出现功能失效。另一方面，L1段的长期磨损，可能会导致配合面表面粗糙度情况恶化，配合间隙加大等，这样也会加大摩擦系数，随着摩擦系数的加大，上述两个方向的失效风险也会加剧，从而进入恶性循环。所以，模具在生产过程中必须进行定期检查和维护，特别是针对斜顶等运动部件，应尽可能避免或推迟失效情况的发生。

3 大角度斜顶的改善方法

在特殊的情况下，如抽芯行程较大、顶出行程受限等，斜顶的顶出角会超出最大安全角度，除了尽可能减少摩擦系数加大安全角度之外，是否还有更可靠的方法呢？

从上述斜顶轴向及径向受力分析中，可以发现一个重要的参数，那就是斜顶下端的一个径向合力Nz，它是产生径向力的源头，并进而产生摩擦力，也是图5中使斜顶杆产生挠度变形的F力。图6所示为这种平行导向杆结构可以直接减少或消除力Nz。

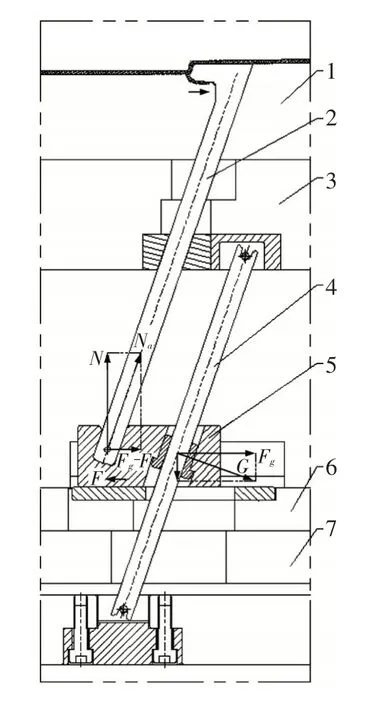
图6 大角度平行导向杆斜顶结构

辅助导向杆和斜顶平行，上下两端分别固定在动模板和动模座板上，当顶出力向上推动顶杆垫板时，辅助导向杆对滑座的压力会产生一个向右的分力Fg，这个力Fg在消除顶杆垫板对滑座摩擦阻力后，其合力（Fg-F）会与顶出力N再形成的合力Na指向斜顶的轴向，推动斜顶运动，这样基本消除了Nz这个径向力。当然，这种结构的导向杆部分也仍然受摩擦力自锁的制约，其角度并不能任意加大，这个力学模型和前述原理类似，在此不再分析计算。

实际运用中，由于加工精度及配合间隙的存在，向右的分力Fg会存在滞后的风险，并不能达到力学模型的理想状态，但仍然可以很好地保护斜顶杆的运动。

这种结构的缺点是模具上需要有足够的安装空间（可能会和其它顶出产生干涉等），结构的复杂度也更高，加工和装配要求更高。

在此基础上，通过对辅助导向杆及斜顶滑座进行复杂角度的计算拟合，可以解决斜顶斜角度抽芯的同步问题，以下两种结构供参考。

（1）平行导向杆，如图7所示。

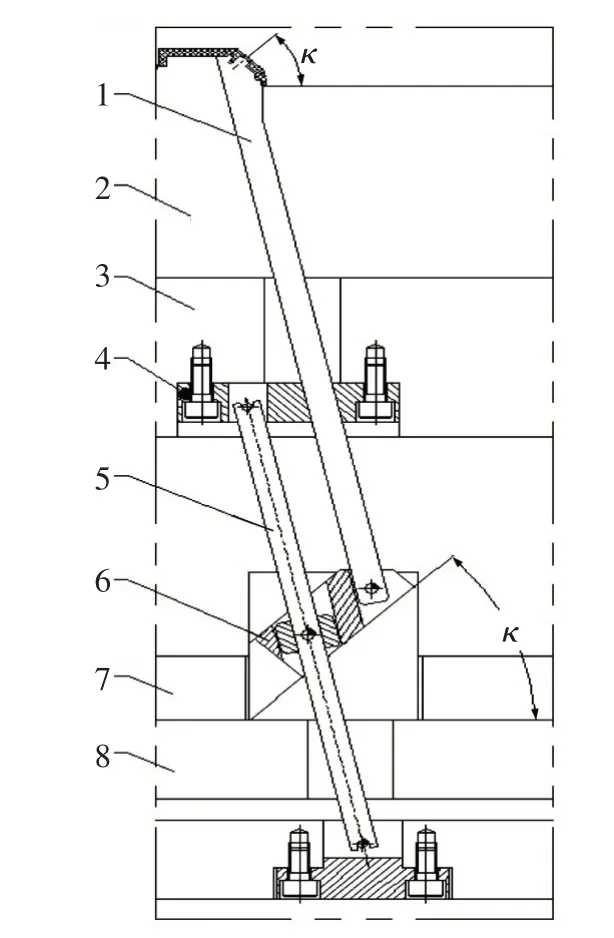
图7 倾斜角度平行导向杆斜顶结构图

斜顶的抽芯方向与分型面存在K角度，常规斜顶方案不能脱模，设计时斜顶滑座也设计为K角度斜面，并利用辅助导向杆来辅助驱动和保持脱模同步。

（2）交叉导向杆双滑座，如图8所示。

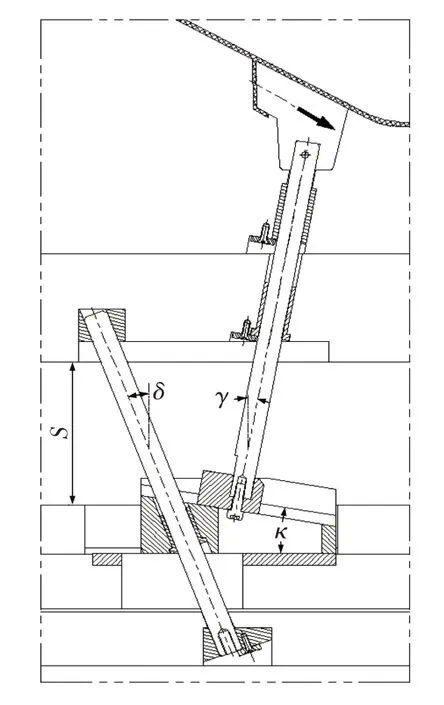
图8 交叉导向杆双滑座结构图

交叉辅助导向杆来需要采用双滑座配合的复合运动，角度计算更复杂，其角度拟合如图9所示。

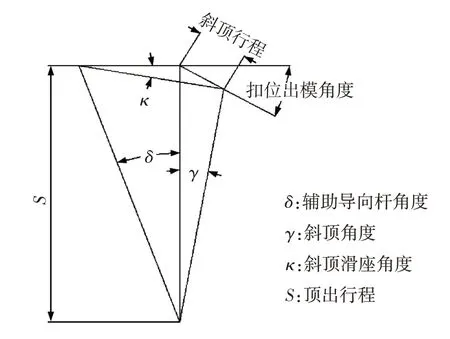
图9 交叉导向杆角度拟合

4 结束语

本文仅是个人的一些理解和分析，水平有限，某些方面自我也感觉不够严谨，难免存在错误或疏漏，仅仅在于抛砖引玉，期待读者批评指正，并进一步探讨。