高频GNSS信号去噪的小波和多方向主成分分析

李保金，李艳艳

( 山东科技大学测绘科学与工程学院，山东青岛 266590 )

0 引言

高频(1 Hz)和超高频(20～50 Hz)全球卫星导航系统(GNSS)定位技术的发展在地震学、气象学和火山学等多种领域的广泛应用[1-4]，对GNSS定位精度提出了更高的要求.影响高频GNSS定位精度的主要因素是GNSS信号中的各种噪声[5].短基线解算时，通过差分定位和误差改正模型可以有效地消除卫星钟差、接收机钟差、卫星轨道误差、对流层及电离层延迟等误差[6]，但难以处理信号中不具有相关性的多路径误差和随机误差.戴吾蛟等[6]指出小波去噪(WD)和经验模态分解(EMD)[7]对信号中的随机误差具有极为显著的剔除效果.敖敏思等[8]指出主成分分析(PCA)[9]方法对多路径误差可以做到有效地提取和消除.此外，GNSS坐标时间序列中还包含有未模型化的系统误差，如影响所有站点的共模误差(CME)[10-11].殷海涛等[12]指出PCA 方法可以有效剔除高频GNSS信号中的共模误差.然而，传统PCA 需要分别依次处理所有站点的 东(E)、北(N)、天(U)方向二维分量矩阵，未考虑所有站点各方向坐标时序的相关性.Tucker[13]于1963年提出了一种新的多元时间序列分析方法：多方向主成分分析(MPCA)，该方法将三维数据矩阵展开成二维数据矩阵，然后进行传统PCA，弥补了传统PCA 忽视各坐标分量之间相关性的缺陷.

针对GNSS的噪声特性，张昊楠等[14]于2013年提出了WD-PCA 组合方法，卢辰龙等[15]于2014年提出EMD-PCA 的组合方法.这两种组合方法较单一滤波方法均能有效削弱多路径效应及高频随机噪声，但都未考虑各坐标分量之间相关性.为了充分利用测站不同分量之间的相关性，本文采用WD-MPCA组合方法对高频GNSS信号进行去噪，以提高高频GNSS的定位精度.并与EMD-PCA 和WD-PCA 两种组合方法的去噪结果进行比较，以证明本文方法的优越性.

1 去噪原理

1.1 EMD方法

EMD于1998年由Huang 最先提出，该方法广泛应用于数据分析领域并取得成功.EMD依据信号本身的固有特性，自然地将信号分解成有限个本征模函数(IMF)和剩余信号.这些IMF是在不同时间尺度上筛选出的单一频率的波，无需进行频域上的变换.IMF必须要满足以下条件：由极值构成的上下包络线均值为0且包络线上极值数与信号过零点数在数量上相差不超过1.

1.2 小波去噪方法

小波变换相较于傅里叶变换改进了基函数，不再受傅里叶变换正弦函数假设的限制，使得非稳定信号可以在多尺度上分析. 离散小波变换(DWT)的原理如下：

对信号进行WD时，通常先将信号按层分解，然后利用阈值剔除每层噪声对应的高频小波系数，最后重构信号.该方法的去噪效果受到选取的小波基、阈值计算方法、阈值处理方式，小波分解层数的制约.小波基的选取通常综合考虑其正交性、紧支性、正则性、对称性和消失矩以做出判断[20].通过MATLAB软件不断调试，本文WD选取db8小波对信号6层分解，得到了消噪效果好且具有良好光滑性的结果.在阈值选取策略上选择了分层阈值降噪的Birge-Massart 算法，该方法自适应的针对每层小波系数的特点采用不同的阈值，具有显著的降噪效果.同时考虑到硬阈值函数造成的小波系数不连续和半软阈值函数实现起来较为困难，阈值函数选择WD中最常用的软阈值函数，使信号最终尽可能平滑.

1.3 PCA 和MPCA 方法

PCA 把多变量的信息用少量综合变量表示以达到降维的目的[21].它通过构造相互正交的分量来消除变量之间的相关性，依据分量贡献值决定保留的信息，最终用尽可能少的变量进行分析[15].

2 高频GNSS数据处理

2.1 高频GNSS数据及解算

图1为美国南加州实时GNSS观测网络(CRTN)选取的试验网中10个GNSS连续观测基准站组成.采样频率为1 Hz，由于数据量较大，选取的时间为2016年年积日100天04:00:00—05:00:00(3 600历元)的观测数据.数据处理所使用的软件为GAMIT/GLOBK软件中用于运动学分析的TRACK 模块.P503站作为TRACK 模块双差定位的基准站，采用短基线模式，解算数据类型为LC，数据回代方法选择smooth，解算结果坐标表示为N、E、U，卫星截止高度角为5°，运行该模块得到测站各方向上的坐标时间序列.

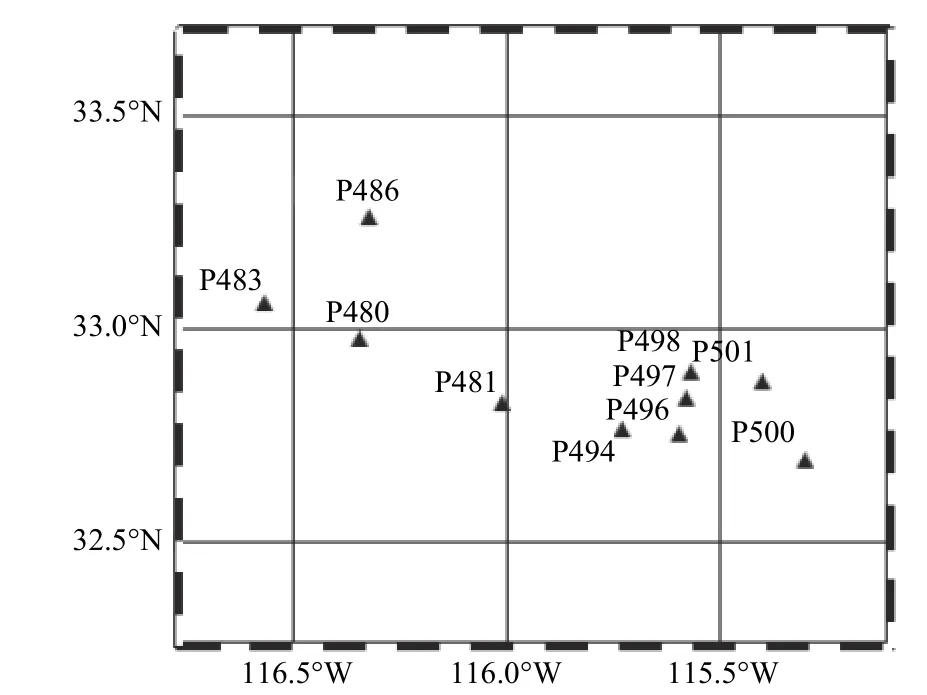
图1 美国南加州CRTN 观测网络中高频GNSS测站分布图

2.2 实验结果及分析

为验证本文方法的有效性，其去噪结果与EMDPCA 和WD-PCA 组合方法的去噪结果进行比较.由于篇幅限制，本文仅以P494测站为例，去噪结果如图2所示.

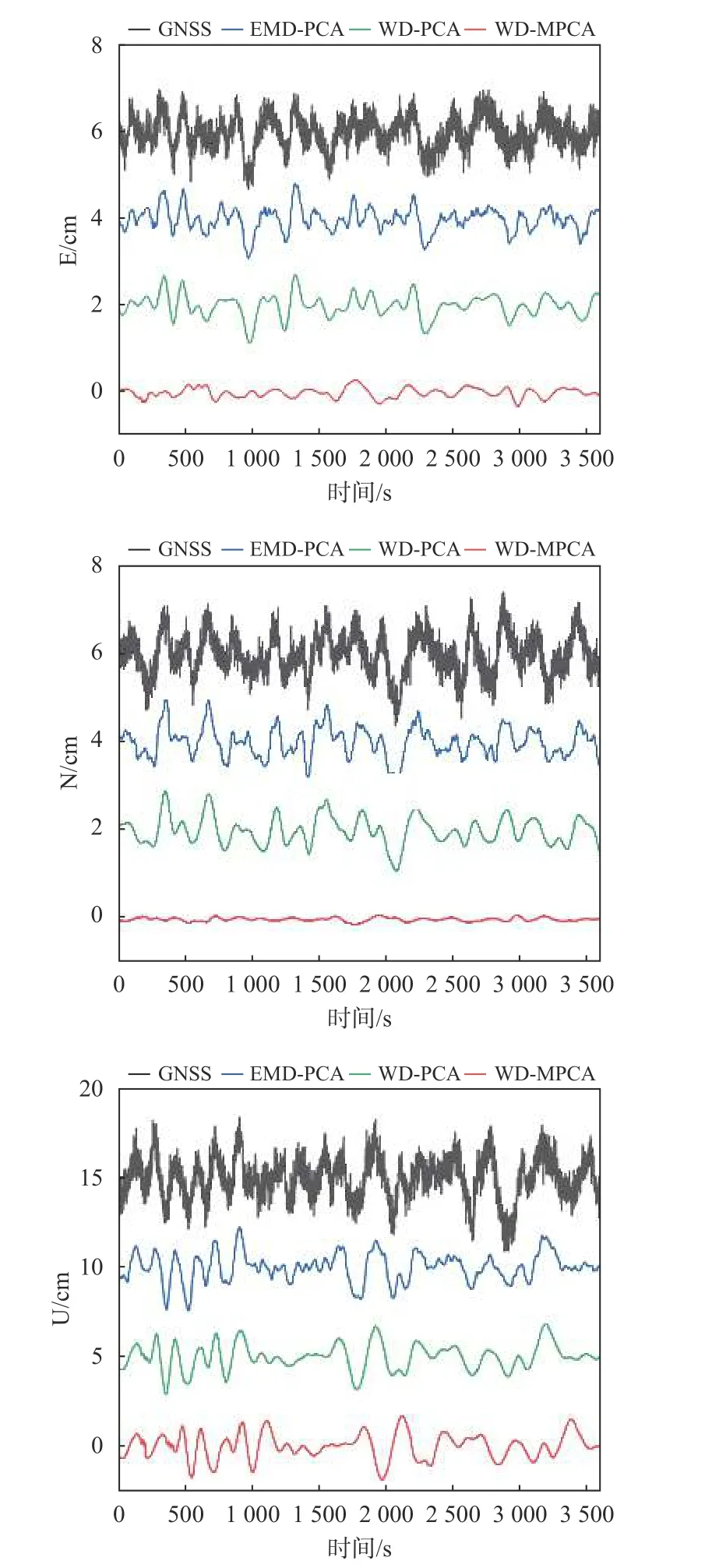
图2 P494站滤波前后GNSS残差时间序列对比图

由图2可知，从滤波前后GNSS残差时间序列对比中可以明显观察到cm 级波动和高频随机震荡.这说明原始信号中含有低频有色噪声(CN)和高频随机白噪声(WN).这些噪声主要是未能在双差模式下消除的误差，低频CN 可能是由重复性的多路径误差[22]和同时影响所有站点的未模型化的共模误差[10]引起的.高频随机WN 则主要是来自接收机自身.三种方法对原始时间序列都有明显的去噪效果，WD-MPCA方法水平方向上的滤波相比另外2种组合方法效果更为显著.垂直方向上三种方法的去噪效果十分近似，对低频噪声的剔除效果较差.这可能是由于误差影响，使得GNSS定位结果的垂向精度通常会明显低于水平分量精度且相差2～3 倍[23].WD-MPCA 组合方法结合WD和MPCA 两种方法的优势，在极大限度削弱随机WN 的同时，有效地剔除了低频噪声.因为考虑了站点三个坐标分量之间的相关性，其滤波效果总体来看明显优于另外两种组合方法.

图3为滤波后滤除的误差曲线对比图.表明三种方法滤除的误差曲线中都有cm 级波动和高频随机震荡，水平方向上WD-MPCA 组合方法滤除的误差曲线相较于其他两种组合方法有更明显的波动，垂直方向上三者波动程度近似.总体来说WD-MPCA 组合方法对时间序列中低频CN 和高频随机噪声具有更为有效地滤除效果.

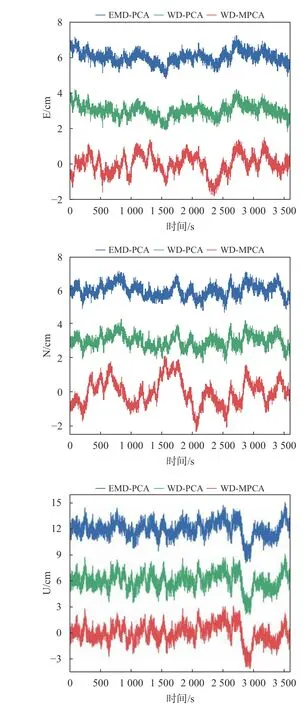
图3 P494站滤波前后滤除的误差曲线对比图

图4为定量描述GNSS定位精度的提高程度，给出了各个方法在各个测站残差时序的中误差.由图4可以看出，各方向三种滤波中误差相较于原始残差时间序列中误差均有明显的降低，说明三种组合方法都能够有效降低信号中的噪声.在三个方向上，EMDPCA 组合方法的中误差略高于WD-PCA 组合方法的中误差，因为EMD跟小波去噪的效果相当[6]，所以两种组合方法得到的中误差也大致相当.在水平方向上，WD-MPCA 组合方法显著优于其他两种方法，其原因是充分考虑了不同测站的三个坐标分量之间相关性.在U 方向上，可能因为垂向上卫星几何分布致使该方向精度较低，导致WD-MPCA 组合方法得到的中误差仅略低于WD-PCA 组合方法，优势不明显.综合来说WD-MPCA 组合方法更能有效降低信号中的噪声.

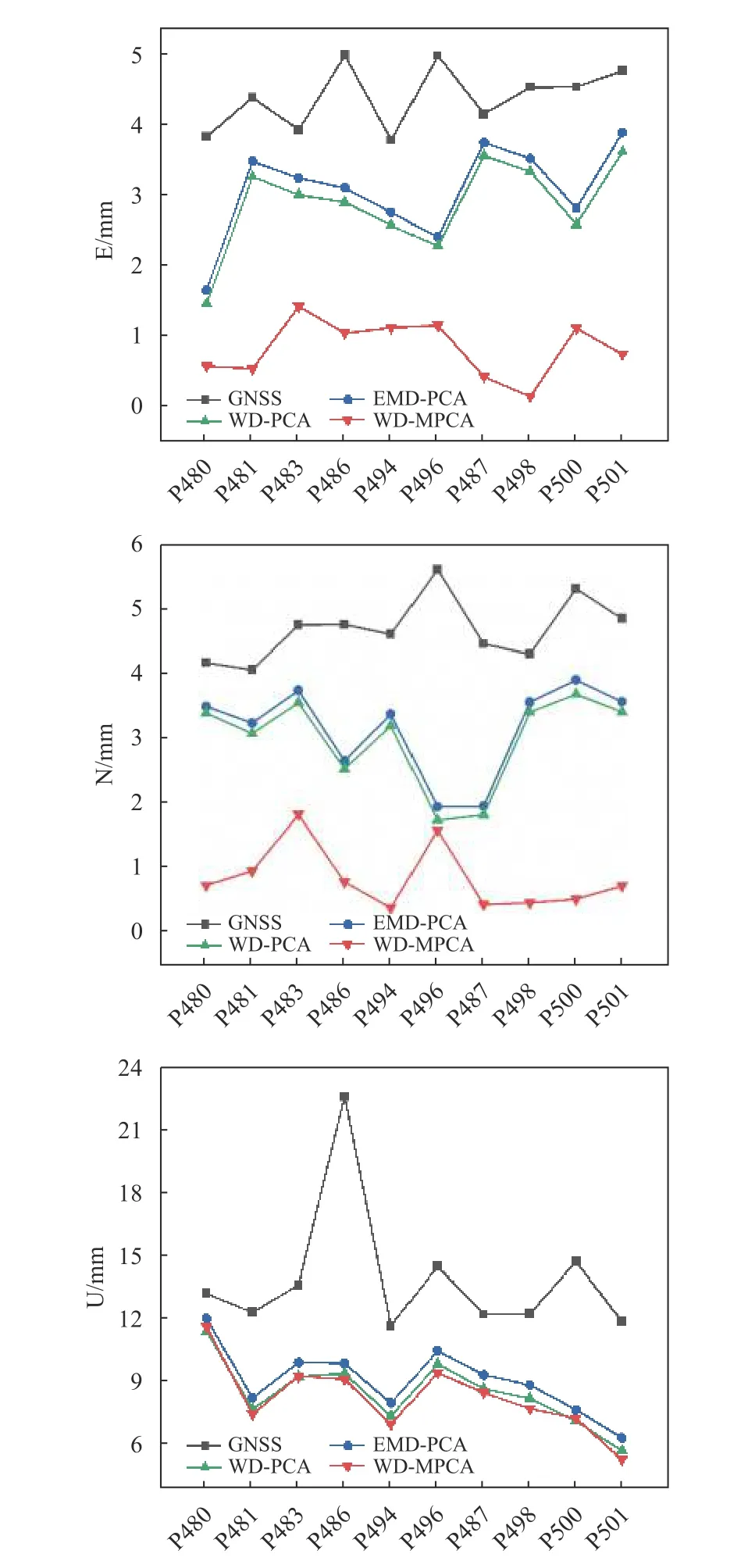
图4滤波前后中误差比较图

表1为比较滤波前后10 个GNSS站的残差时间序列的平均中误差.从表中可以看出WD-MPCA 组合方法得到的平均中误差小于其他组合方法，经WD-MPCA 组合方法去噪后，其平均中误差分别为0.83 mm、0.85 mm 和8.30 mm，相比原始时间序列平均中误差分别有81.14%、81.91%和40.37%的降幅.考虑了测站不同方向坐标时序相关性的WD-MPCA组合方法相比另外两种组合方法，在其基础上进一步的剔除噪声，可以明显消除水平方向上的噪声和垂直方向上的部分噪声.

表1 滤波前后10个GNSS站的残差时间序列的平均中误差mm

功率谱密度(PSD)可以用来表征每个测站的高频GNSS定位结果中的噪声信息[1].对测站进行功率谱密度估计得到滤波前后残差时间序列的功率谱密度比较图如图5所示，在原始信号的残差时间序列中可以明显观察到信号中含有高频WN 跟低频CN.由图5中可知，在10～100 s周期内的高频WN均能被三种滤波方法有效消除.对于在100～103s 周期内的较高频CN 和103～104s周期内的低频CN，在水平方向上，WD-MPCA 组合方法明显优于EMD-PCA和WD-PCA 组合方法.其主要原因是充分考虑了各测站不同分量之间的相关性，极大限度剔除高频噪声的同时，有限剔除了共模误差和多路径误差.在垂直方向上，可能受精度的制约导致效果不明显，但是仍然可以看出该方法能够剔除垂直方向上的部分噪声.综合来说，与EMD-PCA 和WD-PCA 组合方法相比，WD-MPCA 组合方法更具有优越性.

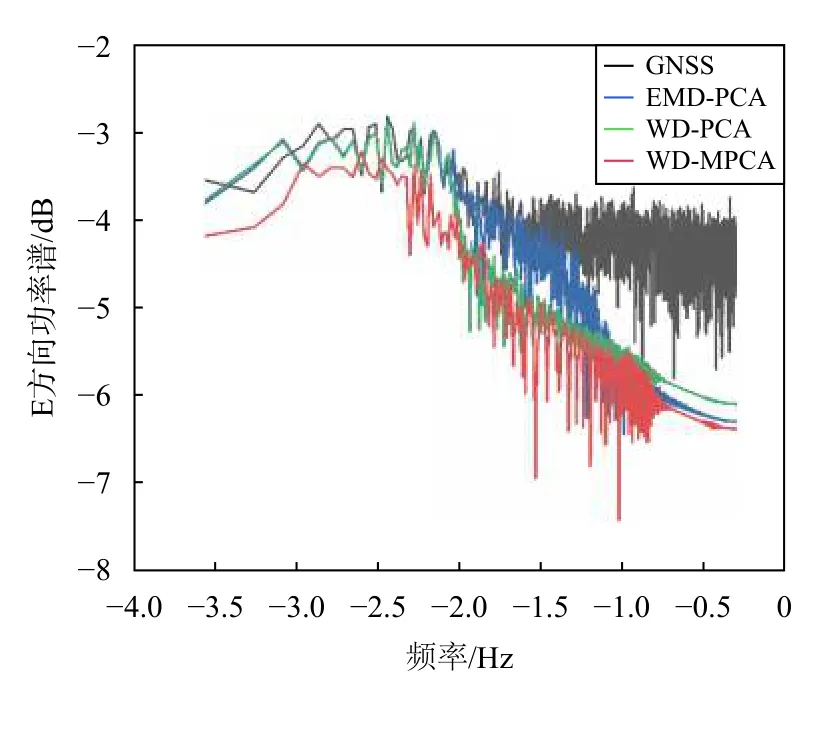
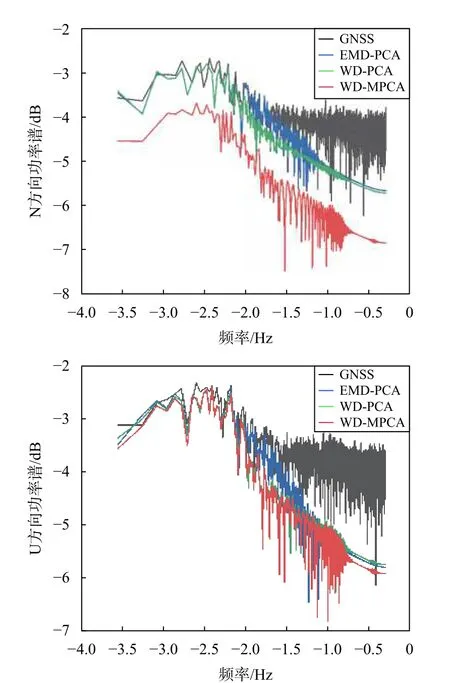
图5 P494站滤波前后残差时间序列的功率谱密度比较图

3 结束语

高频GNSS观测结果中不可避免的含有各种观测误差，这严重降低了GNSS的定位精度和可靠性.因此，需要采用高效去噪方法来消除高频GNSS观测结果中的低频噪声和高频随机噪声，以提高其定位精度和可靠性.

本文采用WD-MPCA 组合方法对高频(1 Hz) GNSS数据进行去噪，结果表明可以有效地消除测站坐标时间序列中的高频WN和低频CN. 谱分析结果显示：WD和EMD方法可以很好地剔除高频随机噪声，但是难以剔除信号中由多路径误差和共模误差引起的低频CN.PCA 可以削弱低频CN，但未考虑各测站不同分量之间的相关性.MPCA 方法在传统PCA 方法的基础上进一步考虑了各测站不同分量之间的相关性.与EMD-PCA 和WD-PCA 组合方法相比，WD-MPCA组合方法精度最高，该方法充分利用不同测站不同分量间的相关性，较好地增强了对噪声的提取能力，有效地提高了GNSS定位精度.