激发学生内驱力，促进深度学习

李砚霞

北京师范大学教育学部郭华教授认为，“深度学习是指在教师引领下，学生围绕具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程。”教育家苏霍姆林斯基也说过：“在人的内心深处，都有一种根深蒂固的需要，就是希望自己是一个发现者，研究者和探索者。”只有激发学生学习的内驱力，把“要我学”变成“我要学，我要积极地学”，才能促进学生深度学习。下面，笔者结合小学数学《圆的认识》一课教学实践，谈谈这方面的探索。

一、丰富视域，激发学生深度参与

学生对概念定义的理解往往是概念的表象开始。数学源于生活，又回归生活。在日常教学过程中，从学生的生活经验出发，充分展示生活中物体的图片或视频，罗列素材，开阔学生的视野，丰富学生的知识视域，激发学生深度参与的欲望。

笔者在教学《圆的认识》一课时，新课伊始，课件首先出现一段视频：在柔和流淌的音乐中，随着充满滋性的解说，出现水中泛起圆形的涟漪、大树的年轮、滚动圆形的车轮、转动着摩天轮、北京天坛公园……美轮美奂，一下子把学生吸引住了，原来很多世界上自然现象、生活物品都是圆形。在学生的认知当中，圆就不仅仅是一个曲线图形，它有丰富的内涵，生活因为有了圆而变得更加生动、精彩、便利。笔者适时进行引导：为什么生活中那么多的现象及物体都是圆形？这其中有什么奥秘呢？车轮制成方形或长方形行不行？碗口为什么要制成圆形的？……从宏观视野丰富学生的认识视域，从而激发学生产生深度学习的求知欲、探究欲与参与欲。

二、任务驱动，促进知识深度建构

学习不是知识简单的传授，而是要在建构知识的过程中，设置任务目标，不断激发学生的内驱力，让学生充满激情地全身心、全程投入到学习中，经历知识的形成过程，深度建构知识体系。让学生成为知识的发现者、研究者、探索者，这样，深度学习才可以达成。

在圆的认识中，最重要的是要引导学生深刻理解“圆心”“半径”“直径”等概念以及“在同圆或等圆内，半径与直径的特征”。那么，如何引导学生深度建构知识体系？在教授这两个内容时，笔者设计两个不同维度的挑战任务引导学生动手操作、观察、交流、表达、比较、小结等，并以核心问题引领学生深度探究，从而构建知识体系。

任务1：独学：探索圆的各部分名称

学生通过个人独学，完成任务1后，再去学习圆心、半径等概念，理解半径与圆规两脚间距离的关系、理解圆心、半径的作用，就水到渠成了。

任务2：共学：小组合作探索圆的特征

任务2是在教师的组织下，学生通过赛一赛、画一画、折一折、量一量、想一想、说一说等多种数学活动方式，理解圆的本质特征：“在同一个圆内，有无数条半径、无数条直径;在同圆或等圆内，所有半径的长度相等，所有直径的长度也相等;直径的长度是半径的2倍”。

《义务教育数学课程标准（2011年版）》指出：数学活动经验需要在“做”的过程和“思考”的过程中积淀，是在数学学习活动过程中逐步积累的。学生在“做”和“思考”中，亲身经历知识的发生、形成过程，深刻理解知识的来龙去脉，从而积累知识经验，发展知识技能，感悟数学思想。

三、凸显本质，引领学生深度思考

数学来源于生活，应用于生活，而且高于生活。运用数学知识可以很好地解决生活中的实际问题，或将学到的数学知识和技能应用于生活实际，体现数学学习的重要价值。但事实上，很多学生很难将数学与生活两者深入地融汇贯通。教师可利用信息技术，虚拟仿真，打破两者间的壁垒，把数学知识与生活现象进行沟通联系，引领学生对问题进行深度思考，提升学生应用知识解决问题的能力。

笔者在教授《圆的认识》一课时，对于“为什么车子的轮胎都是圆？造成方形、长方形或其它形状不行吗？”学生们认为：“因为车轮很圆很光滑，适合滚动。如果车轮设计成方形或长方形，很平，不会滚动。”可见，学生只是表面上理解“在同圆里，圆心到圆上一点的距离处处相等。所有的半径都相等”，但还未深入理解知识在生活中的应用。教师可适时应用Flash制作的仿真多媒体动画进行教学：小猴子分别坐在方形、椭圆形、圆形轮子的车子上行进。三辆车的车轴都装在轮子的中央。当看到小猴子坐在方形、椭圆形轮子的车子上，在滑稽的音乐中，上下颠簸，龇牙咧嘴、痛苦而狼狈不堪的样子时，学生们哈哈大笑起来;当看到小猴子坐在圆形轮子的车子上，配合着轻松愉快的音乐在悠然地挥手时，学生们又不由地发出会心的微笑。在教师精心创设的情景中，在笑声中，学生们恍然大悟了：原来车轮做成圆形，车轴的位置放在圆心，是利用“同圆内，所有半径相等”的原理，让车轴与地面的距离保持不变。这样，车子才能平稳快速地前进，人坐在车子上才舒服。

“除了这些，生活中哪些事物或现象也与圆的特征有关联？”一石激起千层浪，有的学生认为，碗口、杯口要制作成圆形，是因为圆形的碗口和杯口，用起来舒畅。用圆杯喝水，也不至于水会从嘴角流出来;有的学生认为，水波纹是圆形的原因是，物体掉进水里，有一定的张力向四周扩散，扩散的力度是一样的，就像圆的半径一样，所以水波纹是圆形的……

史宁中教授说过：“数学知识的形成依赖于直观，教学知识的确定依赖于推理。”通过演示，架起了直观与想象的桥梁，达到“通过现象，看到本质”的目的。在这一过程中，学生的想象、思考、推理、辨证等能力得到了提升，且思维潜力被充分挖掘，使学习真正走进深入。

四、适度拓展，持续发展深度学习

拓展是指在原有知识基础上补充新知识，或者站在知识角度和学情角度，设计知识的延伸点，丰富学生的视野，拓宽学生的思维空间，让学生深度学习、持续发展。

例如，笔者在教授《圆的认识》一课时，课堂进入尾声，笔者对学生进行“圆文化”的拓展。

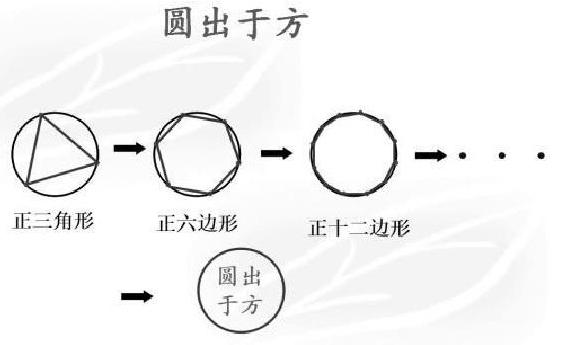
师：早在二千多年前，《周髀算经》记载：“圆出于方，方出于矩”，所谓“圆出于方”，就是说最初的圆形并不是用现在的这种圆规画出来的，而是由正方形不断地切割而来的。

（借助几何画板依次画出正方形、正六边形、正八边形、正十六边形）

师：你们发现什么？

生：随着正多边形边数的不断增加，它们越来越接近圆。

师：你们想到了什么？

生：如果继续增加边数，变成正三十二边形、正六十四边形、正一百二十八邊形……无限地增加下去，会变成一个圆。

随着借助几何画板画出的正多边形的边数越来越多，学生们都按捺不住，不约而同地说：“圆、圆、圆……”当画出正一百二十八边形，学生们一起鼓起掌来：“哇，太圆了！”

师：早在二千多年前，古人就能发现“圆出于方”这个道理，你们有什么想说的呢？

生1：感到特别的自豪和骄傲！

生2：古人实在太厉害了。他们没有信息技术就能发现这个道理，肯定经过无数次的实践。

生3：我们要学习古人锲而不舍的精神和严谨的科学态度。

师：看来，你们的感悟真深。是的，古人对我国的科学文化发展作出了很大贡献，我们不但要学习古人对科学求真的态度，更要把古人留下来的文化精粹传承与发扬下去。

让学生深切体会到“圆文化”的博大精深，激发了学生的民族自豪感，增强了学生的文化自信，丰富了他们的情感，使学生体验了数学的价值，让学生感受到数学发展的不歇动力，有效地促进学生深度学习与持续发展。

通过丰富学生的知识视域、揭示知识的本质，把枯燥的学习变成有意义、有激情的学习，有效促进学生主动学习、深度思考，深度建构知识体系，提升学生数学思维能力与解决问题能力。

责任编辑  吴华娣