基于ANSYS-UPFs的岩土等效线性模型二次开发

金海 黄明镇 高宇航 曾勇文

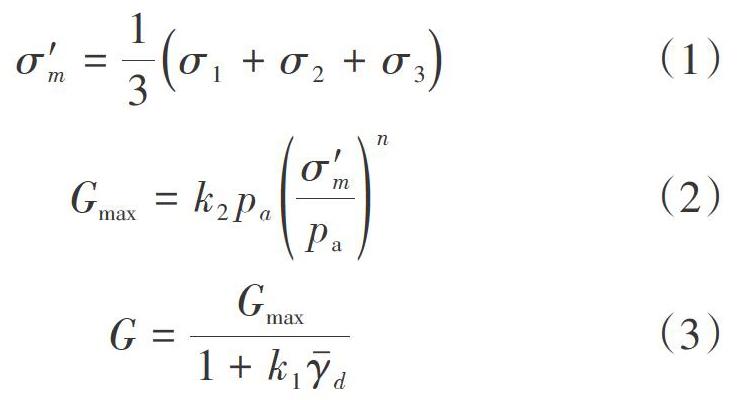
摘要：岩土在动荷载作用下的应力-应变关系非常复杂，在进行土石坝有限元动力分析时，需要选择合适的岩土本构关系模型。基于黏弹性理论的等效线性本构关系模型因其计算效率高、计算结果合理而得到广泛使用。使用ANSYS平台的User Programmable Features（UPFs）开发了基于黏弹性理论的等效线性本构关系模型。使用 SHAKE91说明文件中的经典案例对比分析和土石坝的地震反应分析进行有效性验证，所得结果符合一般规律，验证了该模型的可靠性。结果表明：以ANSYS平台为基础开发的等效线性模型可用于复杂的三维岩土结构的动力分析。研究成果为大型岩土结构工程的动力分析问题提供了一种新的选择。

关键词：岩土等效线性模型;二次开发;ANSYS;岩土动力分析

中图法分类号：TU435文献标志码：ADOI：10.15974/j.cnki.slsdkb.2021.08.014

文章编号：1006 - 0081（2021）08 - 0073 - 04

土石坝等岩土结构动力分析研究的主要难点在于构造有效的土体应力-应变模型来模拟岩土结构在动力作用下的响应。1966年Clough[1]将有限单元法引入岩土力学领域后，Dibaj[2]、Idriss[3]等相继提出了岩土结构的非线性分析方法，直到1972年，Hardin和Drnevich[4]把土体作为黏弹性材料，提出了可以反映土体材料非线性和黏滞性的Hardin-Drnevich等效线性模型。1996年，沈珠江[5]结合等效线性黏弹性模型以及残余应变经验公式，提出了沈珠江等效黏弹塑性模型，可直接计算土石坝在地震作用下的残余变形，又根据大型振动三轴试验结果，对堆石料动力本构模型作了系统研究，改进了堆石料的等效黏弹性模型，在后续土石坝的动力研究中被广泛应用。

本文基于ANSYS-UPFs，结合经沈珠江改进的等效黏弹塑性模型进行二次开发，通过SHAKE91说明文件中的经典案例对比分析和土石坝的地震反应分析进行有效性验证。

1 基于黏弹性理论的等效线性本构模型

在循环荷载作用下，土体会表现出非线性、滞后性和变形累积等应力-应变关系特点。对于某些简单问题，可将三者分别加以考虑，在特定范围内能得到较好的结果。对于复杂问题，则需要将3种特性结合考虑。

1.1 等效线性模型的表达方式

在岩土动力分析中需要考虑动剪切模量和阻尼比这两个参数，在循环荷载作用下，动剪切模量和阻尼比会随着土体剪应变的变化而改变。因此，在等效线性模型中引入等效剪切模量[G]和等效阻尼比[D]的概念，将滞回特性用等效阻尼比[D]与剪应变幅值[γa]的关系反映;而土体的骨架曲线则用等效剪切模量[G]与剪应变幅值[γa]的关系反映。

本文使用沈珠江[5]提出的如下形式确定等效剪切模量[G]和等效阻尼比[D]：

1.2 子程序编制思路

由式（2）可知，坝体的初始剪切模量[Gmax]与震前的平均有效应力有关，因此需在动力分析前进行静力分析，得到各单元的初始应力状态并计算平均有效应力，可通过APDL命令“INISTATE，WRITE，1，，，，，S”将应力状态输出为IST文件。在第一步计算时，通过INISTATE，READ‘保存的文件名，‘IST命令读入单元的初始应力，计算出平均有效应力，进而计算出初始剪切模量[Gmax]。由于在后续计算中需要用到初始剪切模量，且该变量在地震过程中保持不变，因此使用子程序中的状态变量statev（1）保存，在第一步计算的起始步更新 ，后续过程无需修改。

在第一次迭代前假定初始动剪应变为0，并根据式（1）～（4） 确定初始剪切模量比[G1Gmax]和阻尼比[D1]。然后，通过线性分析方法求解得到各单元的剪应变并更新。在一次迭代结束后，通过更新的应变水平按照式（5）～（7）确定各单元的剪切模量和阻尼比，并进入下一次迭代。由于剪切模量比和阻尼比在每次计算中保持不变，在子程序中用statev（2）和statev（3）保存，并在每次计算起始步更新。最大剪应变[γdmax]用statev（4）保存，并在每个增量步进行更新。等效线性模型结构框架见图1。

1.3 岩土材料液化判别

由于地震激励的周期和幅值是不固定的，结构模型频率的取值和边界约束的施加会对计算结果产生较大影响。在实际计算中，可能会使局部单元的剪应变过大。实际上，当土体等效动剪应力大于抗液化动强度时，土体发生液化。在一定振次下达到某一应变标准时的动应力幅值称为土的动强度。

要对土体材料进行液化的判别，需要获取各单元的等效动剪应力和材料动强度。而动强度需要根据材料的动强度与破坏周次关系曲线和地震等效振动次数确定。一般情况下，在后处理中进行液化的判别。本文考虑土体液化对计算结果的影响，在程序中事先设定一个液化应变的判别标准（如取[8%]）、土体液化后剪切模量比（[1%～5%]）和阻尼比（[Dmax～2Dmax]），當剪应变大于设定的液化应变时使用液化后的等效参数。

2 算例验证

2.1 算例1

本例使用费康[6]、谢伦武[7]等的SHAKE91说明文件[8]中的经典算例来验证子程序的可行性和可靠性。算例为一坐落于基岩上的水平地基，由砂土和黏土组成。土体材料参数及相应的等效线性参数见表1。砂土和黏土的剪切模量比、阻尼比与剪应变关系见图2。输入的地震加速度时程曲线见图3。

如图4（a）所示，在ANSYS前处理中建立高45 m（y方向）的土柱进行分析。土柱使用三维八结点SOLID185单元，共剖分为5 632个单元。土体材料使用自定义的等效线性材料参数。最大剪切模量按表1给定值输入。土柱地面施加全约束，顶面无约束，侧面只允许发生x向变形，并沿x向输入地震波，输入的地震波加速度峰值设置为0。图4（b）为最大地震反应加速度沿地基深度分布。本文计算方法与SHAKE91计算方法相比较，加速度沿深度方向的变化符合变化趋势，土层底部加速度的变化很小，在土层中上部加速度变化明显，且上部的加速度放大较为明显。本文方法和SHAKE91求得的土层顶面绝对加速度值分别为0.315 g和0.29 g，误差在容许范围内，约为8.6%。

将输入的地震波加速度峰值调整为0.000 1 m/s2，重复上述计算，得到加速度放大系数与输入的峰值加速度关系曲线，如图5所示。

2.2 算例2

对于一个高100 m、坝顶宽10 m、心墙顶高6 m心墙土石坝，上下游对称，坡比为1∶2，心墙坡比为1∶0.2，如图6所示。土石坝使用三维八结点SOLID185单元，共剖分为14 000个单元，等效线性材料参数如表2所示。输入的河道向加速度按如图7所示加速度时程曲线取最大加速度为0，竖向加速度取河道向加速度的2/3。

观察图8（a）心墙中心线上最大加速度分布，在70 m以下的最大加速度变化不明显，而在70 m以上部分最大加速度随着坝高急速上升，并在坝顶处达到最大，最大加速度分布存在着鞭梢效应。观察图8（b）心墙中心线上最大剪应变分布，在60 m以下变化较小，在60～80 m急速增大，在80 m以上又迅速减小。最大剪应变出现在坝体2/3处，与土石坝受地震作用后，常出现裂缝或产生较大变形的位置相符。

3 结 语

基于ANSYS-UPFs编译了用于岩土动力分析的等效线性本构模型用户子程序，并通过SHAKE91说明文件中的案例建立了三维土层进行对比分析，计算结果符合实际情况，证明了本文基于ANSYS-UPFs开发的等效线性模型的可靠性和适用性。通过土石坝算例的计算以及对计算结果的分析证明了本文方法可利用ANSYS的前后处理优势对大型岩土结构进行应力-应变动力分析。

参考文献：

[1] CLOUGH R W，CHOPRA A K. Earthquake Stress Analysis in Earth Dams[C]// Proc.ASCE，No.EM2，1996.

[2] DIBAJ  M， PENZIEN J. Nonlinear Seismic Response of Earth Structures[R]. Report EERC-69-2，1969.

[3] IDRISS I M，SEED H B，SERFF N. Seismic Response by vari-ble Damping Elements[C]// Proc.ASCE，No.GT1，1974.

[4] HARDIN B O，DRNEVICH V P. Shear modulus and damping in soils design equations and curves[J]. Journal of Soils Mechanics and Foundation Division，1972，98（7）：667-692.

[5] 沈珠江，徐刚. 堆石料的動力变形特性[J]. 水利水运科学研究，1996（2）：143-150.

[6] 费康，刘汉龙.ABAQUS的二次开发及在土石坝静、动力分析中的应用[J].岩土力学，2010，31（3）：881-890.

[7] 谢伦武，熊峰，姚梓渝，等.基于MATLAB和ABAQUS的土体等效线性化方法二次开发[J].地震工程与工程振动，2015，35（1）：135-142.

[8] IDRISSIM，SUN J I. Users manual for SHAKEE91[M].Davis： University of California，1992.

（编辑：李 慧）