变速抽水蓄能和直驱风电系统的阻抗建模及稳定性分析

王方洲，刘开培，秦 亮，陈 满，朱 蜀，杜一星

（1.武汉大学电气与自动化学院，湖北省武汉市 430070；2.中国南方电网调峰调频发电有限公司，广东省广州市 510630）

0 引言

储能与海上风电联合运行可有效平抑海上风电机组输出功率的波动，减缓其对电网稳定运行的冲击［1］。由于海上风电的特殊性，采用海水抽水蓄能方式有较大的优势［2］，南方电网公司正在万山群岛进行海水抽水蓄能系统的建设，并计划与海上风电系统联合运行［3］。变速抽水蓄能机组可以给电力系统带来额外的灵活性，进而改善电力系统的动态性能［4］。本文研究分析对象为可逆式水泵水轮机和双馈 感 应 电 动 机（doubly-fedinduction machine，DFIM）组成的双机式机组［4］。

文献［5］推导了基于DFIM的变速抽水蓄能机组的数学模型，但由于将原动机简化为恒转矩模型，因而无法分析系统超低频段（小于1 Hz）的稳定性。文献［6］给出了换流器的简化模型，但其简化方式会对系统高频段稳定性分析带来影响。文献［7-9］将特征值分析方法应用于变速抽水蓄能机组的稳定性研究中，但文献［7，9］仅在大系统中分析了接入变速抽水蓄能机组后的功角稳定问题。文献［8］仅对电磁部分进行了建模与分析。文献［10-15］对双馈感应发电机（doubly-fedinduction generator，DFIG）与换流器阻抗模型进行了研究，提出可以在同步旋转d-q-0坐标系［15］、相序［14］和相量域［13］中，建立其交流侧阻抗模型的方法。文献［10，12］给出了DFIG的阻抗模型，但文献［10］忽略转子侧变流器（rotorside converter，RSC）和 电 网 侧 变 流 器（grid-side converter，GSC）之间通过电容的耦合作用。文献［12］忽略了不同阻抗模型中换流器交、直流之间的耦合作用。文献［16］给出了直驱风电机组的建模方法。上述文献在线性化过程中，均将锁相环（phase-lockedloop，PLL）相角固定在0°进行线性化，这样会影响PLL相角在不为0°的工况下稳定性分析的精度，且变速抽水蓄能机组中DFIM存在电动工况，因此稳定性还会存在差别。由于水泵水轮机非线性程度较高，当水泵水轮机进行功率控制时，如果不引入水泵水轮机的阻抗模型，则会影响超低频段的稳定性分析结果。

变速抽水蓄能机组采用电压外环和电流内环的双环控制策略来进行直流电压、有功功率、转速和无功功率的控制［5］。目前，变速抽水蓄能机组有3种控制方式［5］：①快速功率控制；②快速转速控制；③以上2种控制的组合。在发电工况下，可采用快速功率控制；在水泵工况下，由于水泵效率和功率是由转速决定的，因此须对转速进行精确控制。为此在实际工程中大都采用快速转速控制［5］，在该工况下的稳定性问题亟须研究。

本文结合多输入多输出（multiple inputmultiple output，MIMO）系统中的传递函数与控制系统传递函数矩阵（transfer function matrix，TFM），将联合运行系统的线性化模型转换到复频域，建立了包含水泵水轮机的变速抽水蓄能机组阻抗模型［17］，并将DFIM转速当作变量引入阻抗建模，以便进行超低频段的稳定性分析。同时，分析了变速抽水蓄能机组与直驱风电机组之间的耦合问题，并对水泵工况进行了分析。

1 联合运行系统拓扑结构

变速抽水蓄能和直驱风电联合运行系统结构如图1所示。

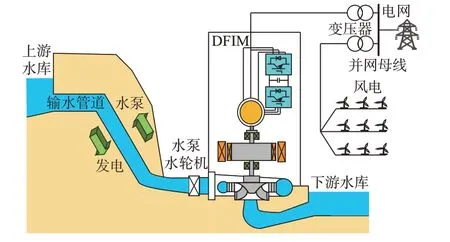
图1 变速抽水蓄能和直驱风电联合运行系统示意图Fig.1 Schematic diagram of combined operation system with variable-speed pumped storage and direct-drive wind turbine

变速抽水蓄能机组采用可逆式水泵水轮机和DFIM，由于发电工况与水泵工况的切换通过换相进行［8］，因此在建模时将水泵与水轮机模型分开处理。直驱风电机组原动机与RSC等效为由输入功率控制的可控直流电源，所有变流器均采用两电平变流器。

2 变速抽水蓄能机组的复频域方程

2.1 水泵水轮机在不同工况下的复频域方程

水泵水轮机系统由三部分组成：引水管道、水泵水轮机和控制器。本文采用文献［18］提出的单引水管道刚性水模型进行系统的暂态稳定性分析。水泵水轮机控制部分的转速和功率控制是一种伺服控制；快速功率控制与快速转速控制下的水泵水轮机也有所差别。附录A给出了水泵水轮机模型与线性化的复频域方程。

2.2 DFIM的复频域方程

DFIM的机械部分如式（1）所示。

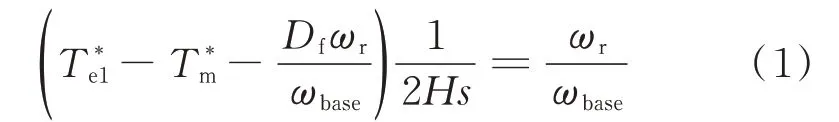
在DFIM电气部分的动态模型中，定子及转子电流和电压通过定转子线圈互感相互影响，其方程如式（2）所示。

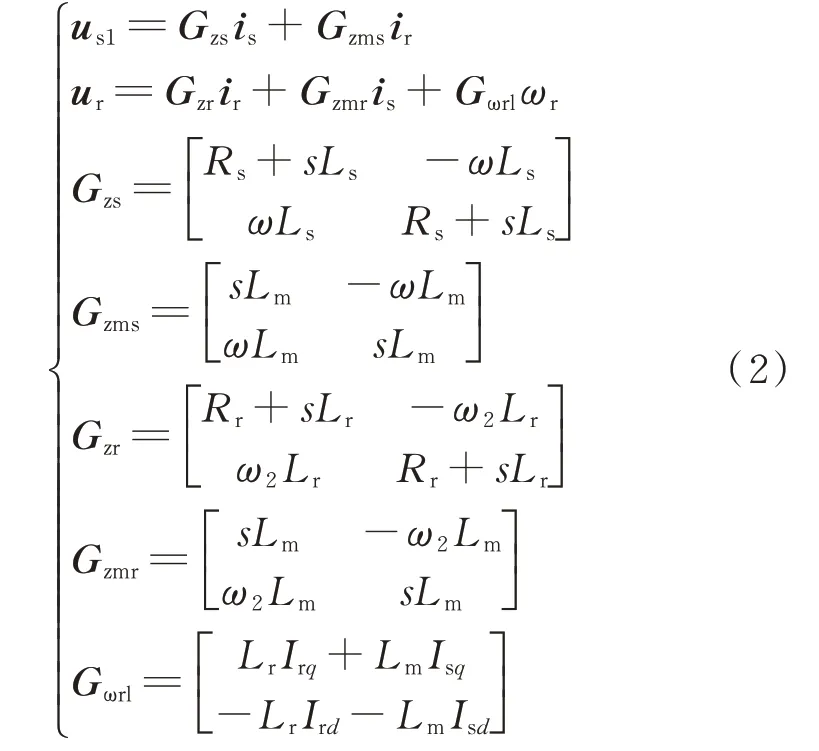
式中：us1、is和ur、ir分别为定子和转子的电压和电流，均包括d轴和q轴上的2个分量；Ls、Lm、Lr分别为定子电感、耦合电感、转子电感；Rs和Rr分别为定子电阻和转子电阻；ωr为转子转速；ω为参考坐标系转速；ω2为ω与ωr之间的差；Gzs、Gzr、Gzms、Gzmr、Gωrl为引入的传递函数矩阵；Isd、Isq和Ird、Irq分别为定子电流和转子电流的d轴和q轴分量稳态值。

为了便于描述，式（1）可表示成如下形式：

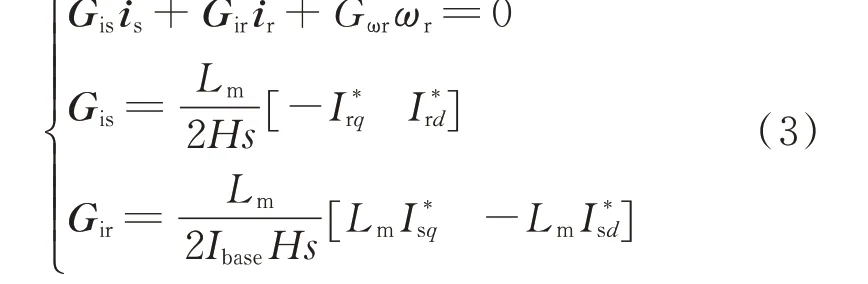
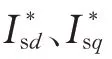
2.3 GSC的复频域方程

2.3.1网侧线路

线路在复频域上的方程为：

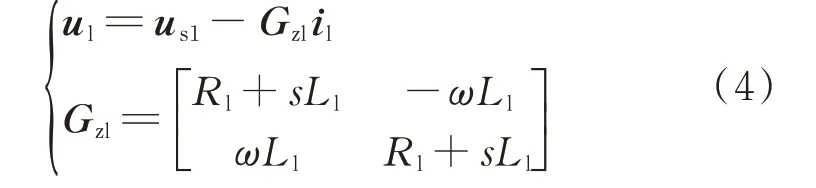
式中：Rl和Ll分别为线路电阻和电感；ul和il分别为定子侧GSC的电压和电流；Gzl为引入的传递函数矩阵。

2.3.2直流电容

直流电容的动态特性代表RSC和GSC之间的耦合关系，其方程如式（5）所示。

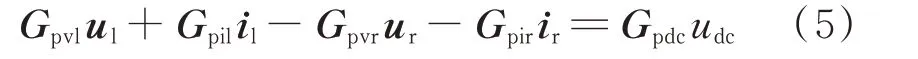
式中：Gpvl=1.5[Ild Ilq]，为引入的传递函数矩阵，其中Ild和Ilq分别为定子侧GSC电流的d轴和q轴分量稳态值；Gpil=1.5[Uld Ulq]，为引入的传递函数矩阵，其中Uld和Ulq分别为定子侧GSC电压的d轴和q轴分量稳态值；Gpvr=1.5[Ird Irq]，为引入的传递函数矩阵；Gpir=1.5[Urd Urq]，为引入的传递函数矩阵；Gpdc=sCDFIMUdc，为引入的控制变量，其中CDFIM为直流线路电容，Udc为直流电压稳态值；udc为直流电压。

2.3.3电网侧外环直流电压控制器

直流电压采用比例-积分（proportional integral，PI）控制器实现，其复频域方程如式（6）所示。

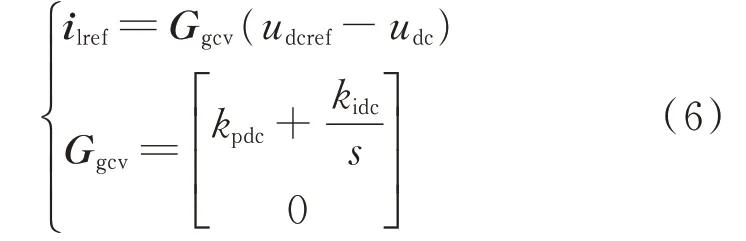
式 中：kpdc和kidc分 别 为 电 网 侧 外 环 控 制 器 比 例 和 积分系数；ilref为电网侧外环控制器输出电流参考值；udcref为直流电压参考值；Ggcv为引入的传递函数矩阵。

2.3.4电网侧内环电流控制器

电流控制器的动态特性包括PI控制、解耦控制和电压前馈控制，取阻抗的基准值为Zbase，其复频域方程如式（7）所示。

2.3.5 PLL小信号模型

所建立PLL小信号模型在θ为任意值时均准确。控制器和电气部分在参考坐标下电压和电流之间的复频域方程如式（8）所示。

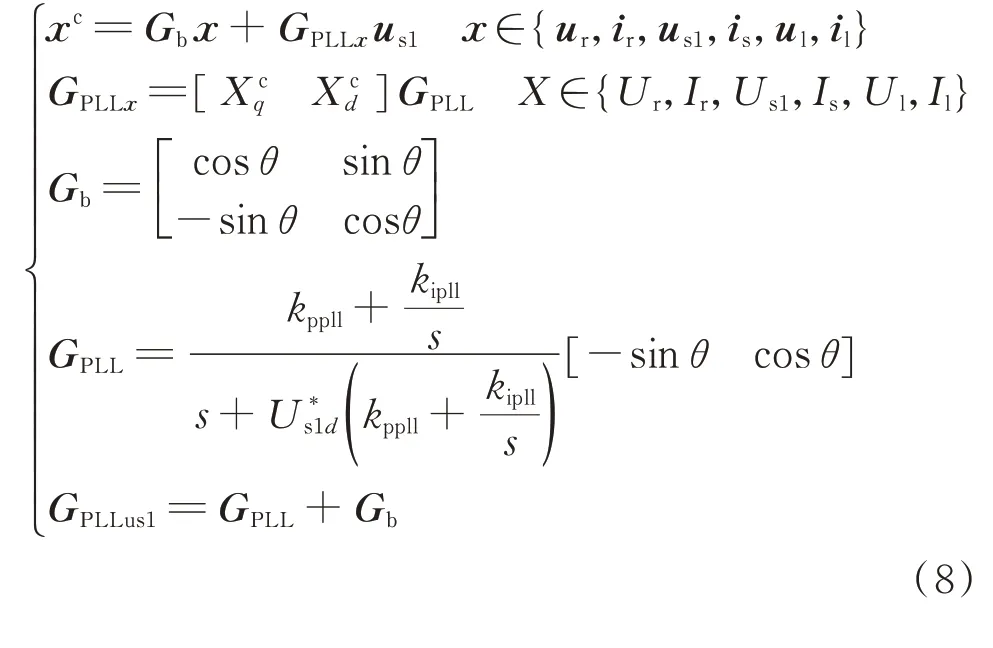
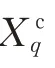
2.3.6 GSC端电压与控制器输出参考电压耦合关系

GSC端电压与控制器输出参考电压的耦合复频域方程如式（9）所示。

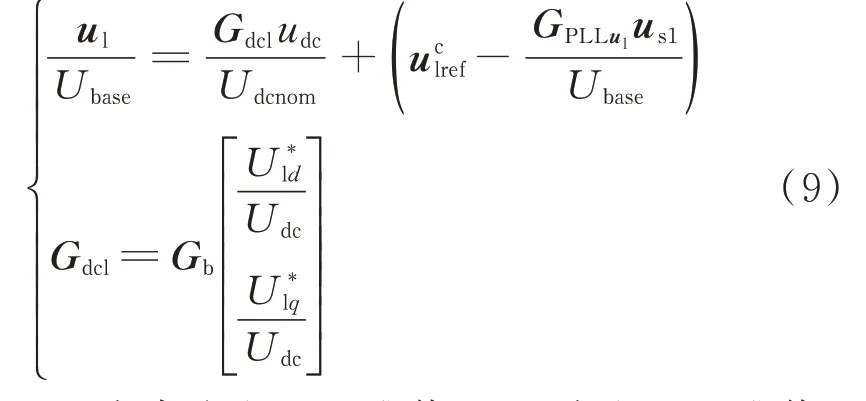
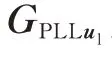
由于耦合问题，DFIM导纳不能直接计算为GSC和RSC导 纳 之 和。

2.4 RSC的复频域方程

RSC的阻抗模型与GSC相似，但转速的变化会影响RSC在低频段的阻抗，本文在复频域方程中引入了转速变量。

2.4.1转速和功率控制器

在快速功率控制模式下，控制器控制有功和无功功率；在快速转速控制模式下，控制器控制转速和无功功率，其复频域方程如式（10）所示。

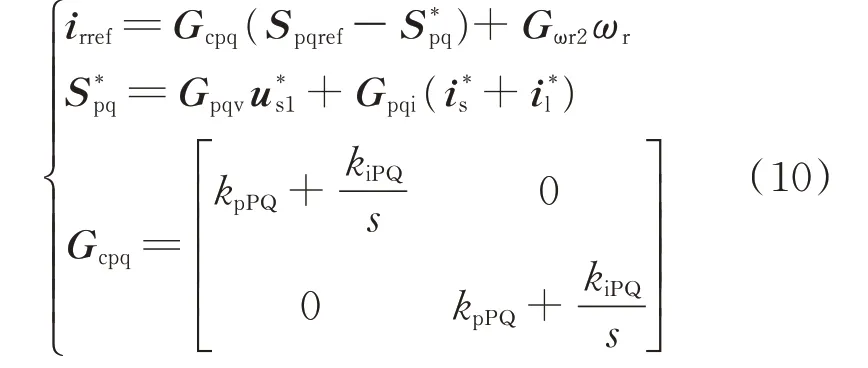
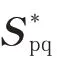
在快速功率控制下，Gωr2=[0 0]T，

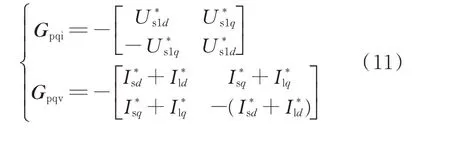
3 联合运行系统的阻抗模型及验证

3.1 直驱风电机组与线路复频域方程

采用等效直驱风电机组代替直驱风电机组，等效直驱风电机组采用双环控制。GSC控制变流器间的直流电压［16］，如附录B图B1所示。直驱风电机组模型包括线圈、直流电容、直流电压控制器、电流控制器、PLL和交直流侧耦合动态模型。具体的复频域方程与相应的传递函数矩阵如附录B所示。

3.2 联合运行系统完整阻抗模型

通过构造传递函数矩阵，在并网母线处，可以得到联合运行系统的完整阻抗模型如式（15）所示。

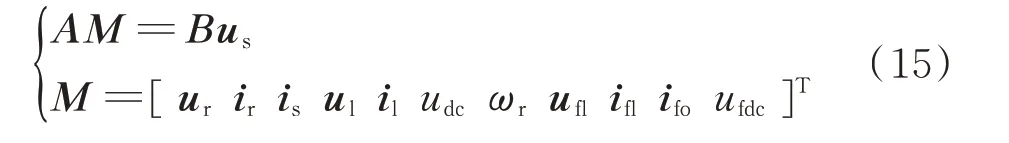
式中：us为并网母线电压，经变压器得到us1和us2；M为 各 变 量 小 信 号 值 矩 阵；ufl、ufdc和ifl、ifo分 别 为 直 驱风电机组变压器二次侧和GSC出口处的电压和电流；A和B为系数矩阵，具体内容见附录C。

最终可以获得19×2转移矩阵Y=A-1B。Ywhole=-Y（17∶18），表示联合运行系统的导纳模型。对导纳模型求逆后，即可得到联合运行系统的阻抗模型Zl。由于生成的模型过于复杂，因此无法以解析表达式形式呈现，但通过相应软件很容易找到符号或数值解。

3.3 模型验证

文献［11，13］介绍了如何通过仿真获得阻抗。在标准工况下系统参数如附录C所示，0.1～200 Hz内 的实测 导 纳Ywhole如 图2所 示。图2中，Ydd、Ydq、Yqd和Yqq分别为Ywhole在dd通道、dq通道、qd通道、qq通道的导纳值。由图2可知，由理论分析得到的导纳与通过扫频法所得导纳基本一致，因而该模型适用于从超低频段到高频段的稳定性分析。

根据图2，由于发电工况（下称工况1）与水泵工况快速功率控制（下称工况2）仅有控制功率正负的变化，其阻抗大致相同。在水泵工况快速转速控制（下称工况3）中，由于控制方式改变，在超低频段阻抗差别较大。

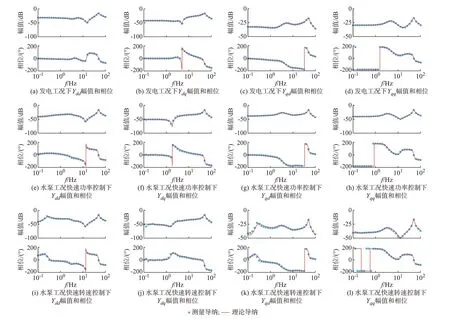
图2 系统的导纳Fig.2 Admittance of system

4 联合运行系统的小信号稳定分析

变速抽水蓄能机组并网运行系统在同步旋转dq-0坐标系下的小信号模型为双输入双输出系统，分析并网系统稳定性时须应用广义奈奎斯特稳定判据（generalizedNyquist stability criterion，GNC）［19］。

阻抗比回率矩阵J定义为：

式中：Zg为电网侧阻抗矩阵。

计算矩阵J的特征函数并绘制奈奎斯特曲线；根据特征函数曲线是否包围临界稳定点（-1，0）可判断并网系统稳定性，特征根轨迹与单位圆的交点处的频率值则代表了系统d轴和q轴的振荡频率［20］。图3给 出 了 在 工 况1、2、3下 的 奈 奎 斯 特 曲线。这些曲线均未包围临界稳定点（-1，0），因此联合运行系统在3种工况下均能稳定运行。

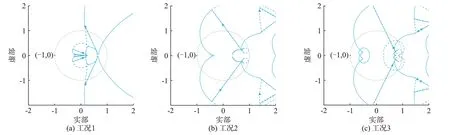
图3 系统奈奎斯特图Fig.3 Nyquist diagram of system

4.1 短路比对系统稳定性影响

电力系统中短路比（short circuit ratio，SCR）的大小可以表示系统并入电网的强弱，用σ表示，σ的计算参考文献［21］。

这里将3种工况作对比，采取线路电阻不变、增加线路电感的方式减小σ，直至σ减小到0.819 6，奈奎斯特曲线逐渐增大，附录C图C1展示了在σ为0.816 9时工况1、2、3的奈奎斯特曲线。附录C图C1表明，工况1和2在σ减小到较低时曲线均未包围临界稳定点（-1，0），系统依然稳定；但工况3下，曲线包围（-1，0），系统失稳，且曲线与单位圆交点对应频率为0.34 Hz，产生了0.34 Hz的超低频振荡，σ的变化对采用快速转速控制方式的工况稳定性影响更大。

4.2 PLL参数对系统稳定性的影响

二阶PLL阻尼比和振荡频率分别为ζ和ωn，PLL的开环带宽为fbw，PLL中PI的系数与其关系参考式（17），通过fbw与ζ可以计算PLL的PI参数。

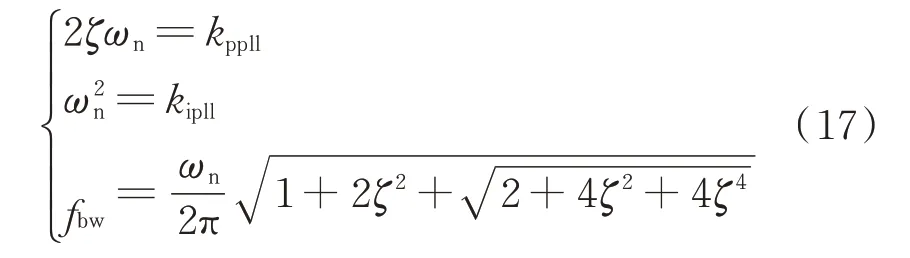
在标准工况下，变速抽水蓄能机组与直驱风电机组的PLL带宽均为10 Hz，阻尼比为0.707，分别维持二者带宽不变，并将阻尼比调至0.01，附录C图C2展示了工况1下二者阻尼比改变后系统的奈奎斯特曲线，工况2与工况3情况与之大致相同。

当变速抽水蓄能机组PLL阻尼比减小到0.01时，系统依然稳定，但当直驱风电机组PLL阻尼比减小到0.01时，图C2（b）奈奎斯特曲线在远处存在交点，曲线包围临界稳定点（-1，0），且与单位圆的交点对应频率为6.053 4 Hz，系统出现了约6 Hz的低频振荡，直驱风电机组PLL阻尼比对联合运行系统稳定性影响更大。

为探究二者阻尼比之间是否存在耦合，使变速抽水蓄能机组PLL阻尼比在0.01～1间改变，直驱风电机组PLL阻尼比在0.01～0.06间改变。根据奈奎斯特曲线对稳定性的判定，可以绘制联合运行系统在二者阻尼比下的稳定域，如图4所示。图4中ζS和ζW分别表示抽水蓄能机组和直驱风电机组PLL阻尼比。

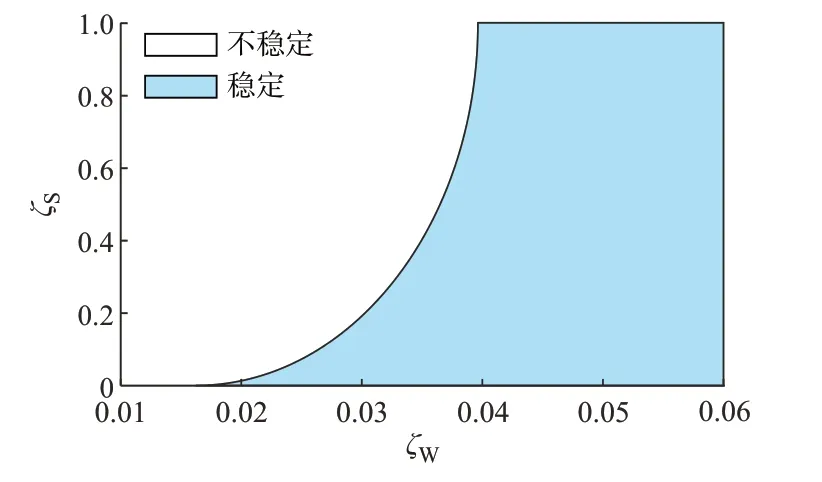
图4 PLL阻尼比稳定域Fig.4 Stability domain of damping ratio of PLL

当变速抽水蓄能机组PLL阻尼比减小时，直驱风电机组PLL阻尼比失稳的临界值会降低，说明二者之间存在耦合，且在一定程度上二者之一的PLL阻尼比减小能够增大另一方的稳定域。

4.3 主要控制器参数对系统稳定性的影响

对变速抽水蓄能机组与直驱风电机组的控制器参数影响进行分析。首先将σ调整为1.56，然后逐渐增大各控制器变量到较大的值。根据奈奎斯特曲线判断系统稳定性情况，如表1所示，失稳代表奈奎斯特曲线包围了（-1，0），稳定代表未出现包围情况。在kpPQ（kiω）与kpgc增大时，稳态值计算会出现异常，本文暂时不分析这3个参数。表1中，kpfdc、kifdc和kpfc、kifc分别为直驱风电机组外环与内环控制器比例和积分系数。

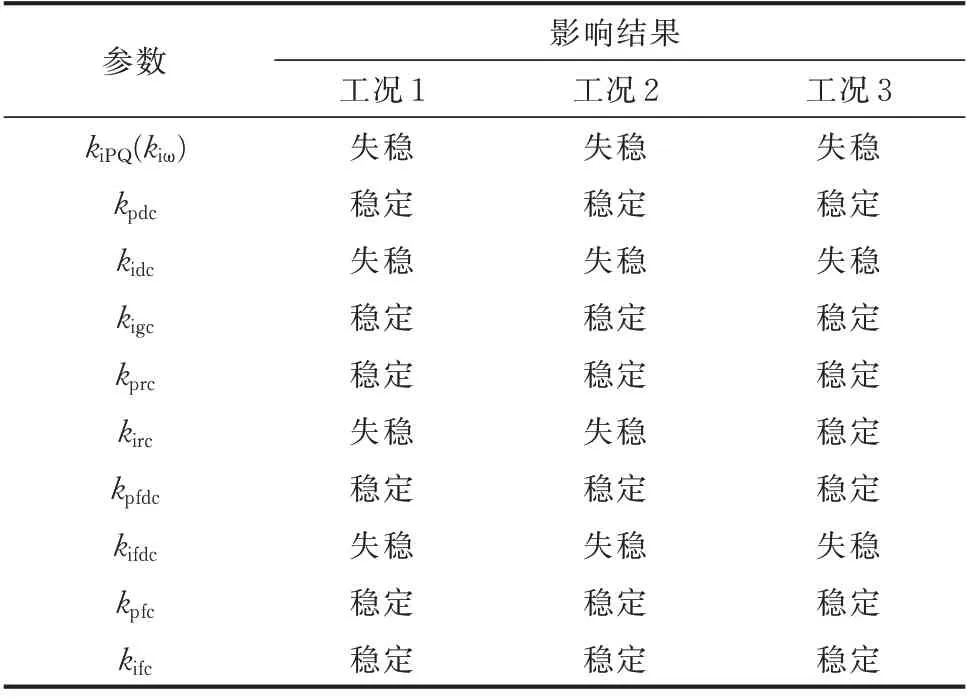
表1 不同工况下控制器参数对稳定性的影响Table 1 Influence of controller parameters on stability under different operation conditions

由表1可以看出，工况1与工况2对控制器参数响应大致相同，工况3因为控制方式的不同导致结果有一定区别，因此选取3种工况响应相同的kifdc、kidc、kiPQ这3个外环控制积分参数研究变速抽水蓄能机组与直驱风电机组间控制器的耦合作用。

以工况1为例，当kiPQ分别增大20、40、70倍时，联合运行系统的奈奎斯特曲线如附录C图C3所示。从奈奎斯特曲线可以看出，kiPQ增大20、40倍时，联合运行系统依然稳定；当其增加到70倍时，奈奎斯特曲线包围临界稳定点（-1，0），系统出现27 Hz的低频振荡失稳。类似地，当kifdc、kidc分别增加50、400倍时，系统同样会出现低频振荡，下面探究这3个参数之间是否存在耦合。

在短路比为1.56的情况下，kifdc、kidc与kiPQ分别在标准工况下扩大50、70、400倍，取一定量的点分别进行计算，通过奈奎斯特曲线判断系统稳定性，得到kifdc与kiPQ、kifdc与kidc的稳定域，如图5所示。

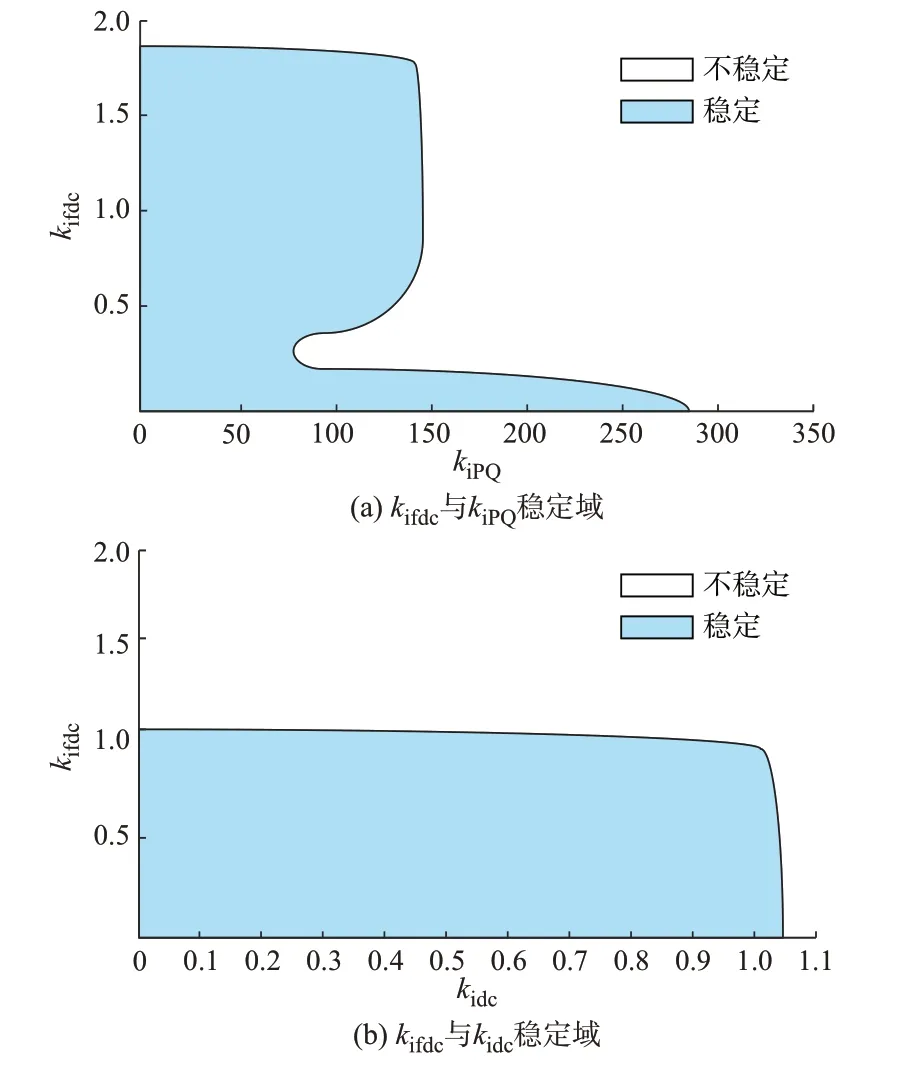
图5 控制器参数稳定域Fig.5 Stability domain of controller parameters

由图5可知，变速抽水蓄能机组与直驱风电机组 的 控 制 器 参 数 之 间 存 在 耦 合，kifdc与kidc之 间 的 耦合关系较kifdc与kiPQ之间的关系要弱。在kifdc与kiPQ之间，当kifdc=0.22时kiPQ的稳定域减到最小，系统更容易失稳。

5 仿真验证

为了验证上述分析的正确性，本文搭建了变速抽水蓄能机组与直驱风电机组联合运行的电磁暂态模型，具体参数与附录C一致。

5.1 SCR对系统稳定性的影响

将σ调整为0.819 6，在此条件下工况2依然稳定，工况3将发生低频振荡，频率约为0.34 Hz。附录C图C4展示了此条件下工况2与工况3并网电流在d轴和q轴上的变化。工况3发生低频振荡，频率约0.328 Hz，与理论分析一致。

5.2 PLL阻尼比对系统稳定性的影响

变速抽水蓄能机组与直驱风电机组PLL存在交互，选取直驱风电机组PLL阻尼比为0.035，变速抽水蓄能机组PLL阻尼比为0.2与0.707，分别进行仿真，如附录C图C5所示。根据奈奎斯特曲线，在变速抽水蓄能机组的PLL阻尼比为0.707、直驱风电机组PLL阻尼比为0.035时，系统失稳频率为5.98 Hz，如附录C图C5（b）所示，失稳频率为6 Hz，理论分析得到的2个参数稳定域与仿真结果一致。

5.3 主要控制器参数对系统稳定性的影响

在 工 况1下，将σ减 小 到1.56，kiPQ=100，kifdc分别设置为0.005、0.220、0.440。根据奈奎斯特曲线，在kifdc=0.220时，系 统 会 出 现15.384 Hz的 低 频 振荡，仿真结果如附录C图C6所示。在该参数下进行仿真，如附录C图C6（b）所示，系统发生了15.6 Hz的低频振荡，与理论分析结果基本一致。

6 结语

在同步旋转d-q-0坐标系下，本文将DFIM小信号模型中的电机转速作为变量，引入水泵水轮机小信号模型，PLL则采用精准的小信号模型，最终建立变速抽水蓄能与等效直驱风电系统的宽频段阻抗模型。然后基于阻抗法对联合运行系统进行了小信号稳定分析，得出以下结论。

1）电网参数发生变化时，在水泵工况快速转速控制方式下系统更容易发生低频振荡，所以在此工况下引入功率转速联合控制方式，可在一定程度上增强系统稳定性。

2）变速抽水蓄能机组的PLL与直驱风电机组的PLL之间存在耦合作用。当变速抽蓄机组PLL阻尼比减小时，直驱风电机组PLL阻尼比的稳定域在一定程度上会增大。

3）变速抽水蓄能机组与直驱风电机组控制器参数存在耦合。当直驱风电机组直流电压控制积分参数值从小到大改变时，存在一个值使变速抽水蓄能机组功率控制积分参数稳定域最小。

下一步工作可以深入研究其他控制器参数对联合运行系统稳定性的影响。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。