基于模糊综合评价法的可控震源振动器平板疲劳可靠性分析与优化

陈 振，李 涛，薛晓伟，周 阳，敬 爽，陈 言

（1.西南石油大学机电工程学院，四川成都610500；2.长庆油田分公司油气技术研究所，陕西西安710018）

可控震源具有激发能量可控、安全环保以及适用于复杂地形的优势，其已成为地震勘探的主要激发装备。但可控震源振动器的平板在恶劣工况下会出现疲劳失效，因此须在设计制造阶段对平板的疲劳可靠性进行评估和优化，以提高其抗疲劳性能。由于影响平板疲劳可靠性的因素（主要包括振动器的结构参数、载荷参数（如液压力）和近地表物性参数等）均具有随机、数据量少等特点，使得平板疲劳可靠性的评估精度低，从而无法对平板的带伤作业状态做出准确的预测，导致物探信号的激发精度显著降低。长此以往，会引发平板疲劳断裂，迫使可控震源停机检修，甚至返厂更换平板，严重降低了地震激发作业的效率。

目前，针对复杂工况下结构可靠性的研究较多，其中用于疲劳可靠性分析的主要有S—N曲线法和断裂力学法。为了研究尺寸参数对结构疲劳可靠性的影响，王文静等［1］考虑焊接板的厚度效应，提出了基于表面外推的热点应力法，并对S—N曲线进行修正，以更准确地分析焊接结构的疲劳可靠性。为了分析载荷对结构疲劳可靠性的影响，朱顺鹏等［2］提出了一种高温低周疲劳-蠕变寿命预测模型，能够综合反映加载方式、保载时间和平均应力对结构疲劳损伤的影响，其精度优于其他基于应变能损伤的寿命预测模型；Hu等［3-4］将铁轨摇枕离散化，并基于离散点处疲劳失效的统计相关性建立了异维干涉模型，准确评估了铁轨摇枕在复杂随机载荷作用下的疲劳可靠性；陈惠亮等［5］提出了一种基于6σ概念的疲劳可靠性计算方法，综合考虑了载荷和几何尺寸的不确定性对平板疲劳可靠性的影响。但是，上述疲劳寿命预测模型的适用范围较窄。为此，吕志强［6］基于Walker准则，考虑了不同材料对平均应力影响的灵敏度，将灵敏度参数引入SWT参数模型（由Smith、Watson和Topper三人共同提出），提出了适用于不同材料的疲劳寿命预测模型。为研究微观裂纹扩展对结构疲劳可靠性的影响程度，李政鸿等［7］针对多孔多裂纹平板的疲劳裂纹扩展问题，提出了基于Eshelby夹杂理论和权函数法的求解方法，并结合Paris裂纹扩展公式预测了飞机结构的疲劳裂纹扩展寿命；Shahani等［8］基于无裂纹扩展和慢速裂纹扩展理论，得到了直升机翼梁的最小扩展裂纹长度及其疲劳裂纹扩展寿命；Corbetta等［9］针对平板的疲劳裂纹扩展现象，提出了基于马尔可夫链的自适应随机动态空间模型，其可准确预测平板的剩余疲劳寿命；Grbović等［10］针对飞机焊接部位的疲劳失效问题，提出了基于扩展有限元法（extended finite element method，XFEM）的数值模拟法，并对飞机焊接部位的疲劳寿命进行了预测；Dong等［11］将焊接接头在复杂随机载荷作用下的裂纹轨迹描述为半椭圆，并结合Kriging插值模型与自适应程序，对焊接接头的疲劳可靠性进行了评估。随着概率统计学在微观裂纹扩展中的应用，Doshi和Han等［12-13］考虑了载荷、材料参数以及疲劳裂纹扩展参数的不确定性，采用贝叶斯方法对船舶结构的疲劳可靠性进行了预测；Yuan［14］等针对飞机结构疲劳可靠性分析时各参数存在的不确定性，基于贝叶斯裂纹平均扩展原则，将3种裂纹扩展模型进行组合，提高了疲劳可靠性分析结果的鲁棒性。

然而，上述针对结构疲劳可靠性的分析存在理论模型过于复杂，疲劳寿命与其影响因素的关系曲线难以确定以及评估时未综合考虑宏、微观因素等问题，故本文采用模糊综合评价法来定量分析基于S—N曲线法和断裂力学法的可控震源振动器平板疲劳可靠性分析模型，以确定2种疲劳可靠性分析模型的权重，得到平板疲劳可靠性的模糊综合分析模型；同时，根据振动器的宏、微观参数，对其平板的疲劳可靠性进行优化设计，旨在为平板的疲劳可靠性预测及优化提供一定的理论指导。

1 可控震源振动器平板动力学分析

1.1 可控震源振动器的结构

可控震源振动器是一个可连续产生振动信号的激发装置，主要由提升缸，双导柱，活塞杆，上、下十字，重锤和平板构成，如图1所示。振动器的平板采用矩形钢板焊接而成，其结构如图2所示。平板中部的2对心形加固板上设有4个通孔，用于安装连接重锤的下十字底座；平板内部焊有由矩形管和矩形板构成的加强骨架，以保证整体的刚度和强度。

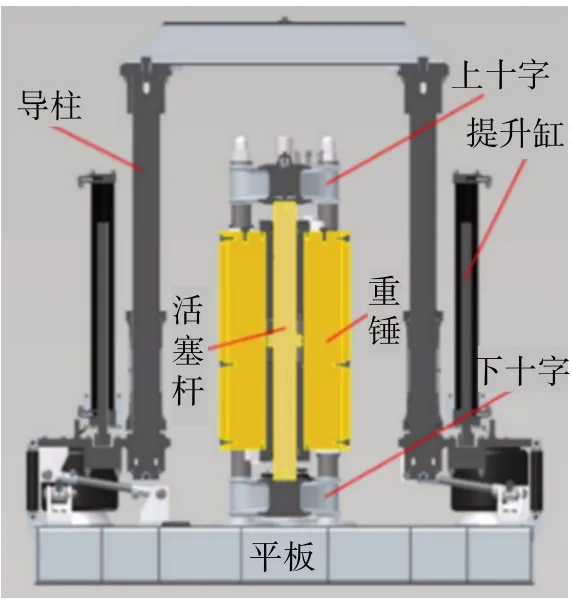
图1 可控震源振动器剖面图Fig.1 Cross-section view of vibroseis vibrator

图2 振动器平板结构示意Fig.2 Structure diagram of vibrator baseplate

1.2 平板动力学仿真正交试验设计

在可控震源振动器激发地震波的过程中，活塞杆上、下端面在交变液压力交替作用下产生激振力并传递到平板上，从而引起大地振动，形成扫描地震信号。由此可知，振动器平板的疲劳特性与振动器的结构参数（活塞杆端面面积A和下十字柱直径D）和载荷参数（交变液压力峰值P）紧密相关。基于此，采用三水平三因素正交表来设计平板的动力学仿真正交试验，如表1所示。

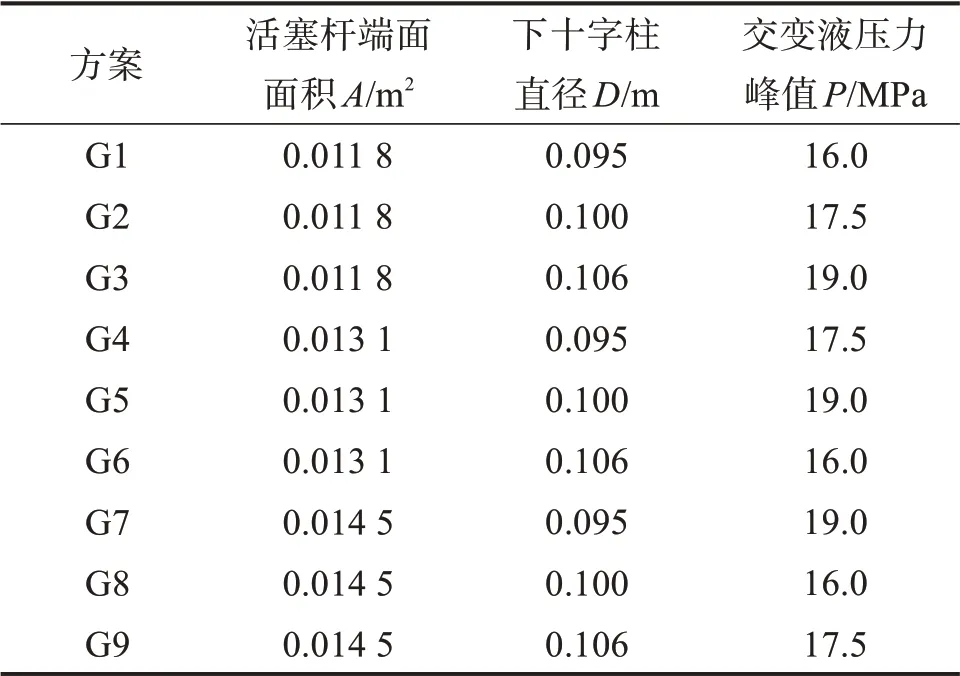
表1 平板动力学仿真正交试验方案Table 1 Orthogonal test schemes for baseplate dynamics simulation

1.3 平板动力学仿真分析

基于设计的9个正交试验方案，开展振动器平板动力学仿真分析，得到平板的疲劳关键部位及其等效应力曲线。

平板所受的外载荷主要包括振动器重力、重锤力以及交变液压力。根据振动器的设计参数可知，其重力为272 kN，均匀作用在平板的4 个空气弹簧座上；重锤力为36 kN，均匀作用在平板的2个心形加固板上；交变液压力的最大峰值为平板输出力峰值的70%。平板输出力Fd的函数表达式为：

式中：xb为平板位移幅值；Gs为大地的弹性系数，Gs=1.061×108；Gv为大地的阻尼系数，Gv=4.271 4×105；ω为振动器液压力的角频率，ω=30π rad/s。

平板动力学仿真模型的边界条件为：大地底部及四周施加6个自由度的约束，并将大地与平板之间设置为对称接触类型，从而真实地模拟平板与大地之间的相互作用。

1.4 平板动力学仿真结果及分析

1.4.1 平板疲劳关键部位确定

利用有限元仿真软件分析得到振动器平板的应力分布情况，最终确定激发地震波时平板的疲劳关键部位主要为：部位1，心形加固板与平板盖板焊接处；部位2，压重底座与平板侧板焊接处；部位3，平板盖板与侧板连接处；部位4，平板侧板与底板角焊接处，如图3所示。

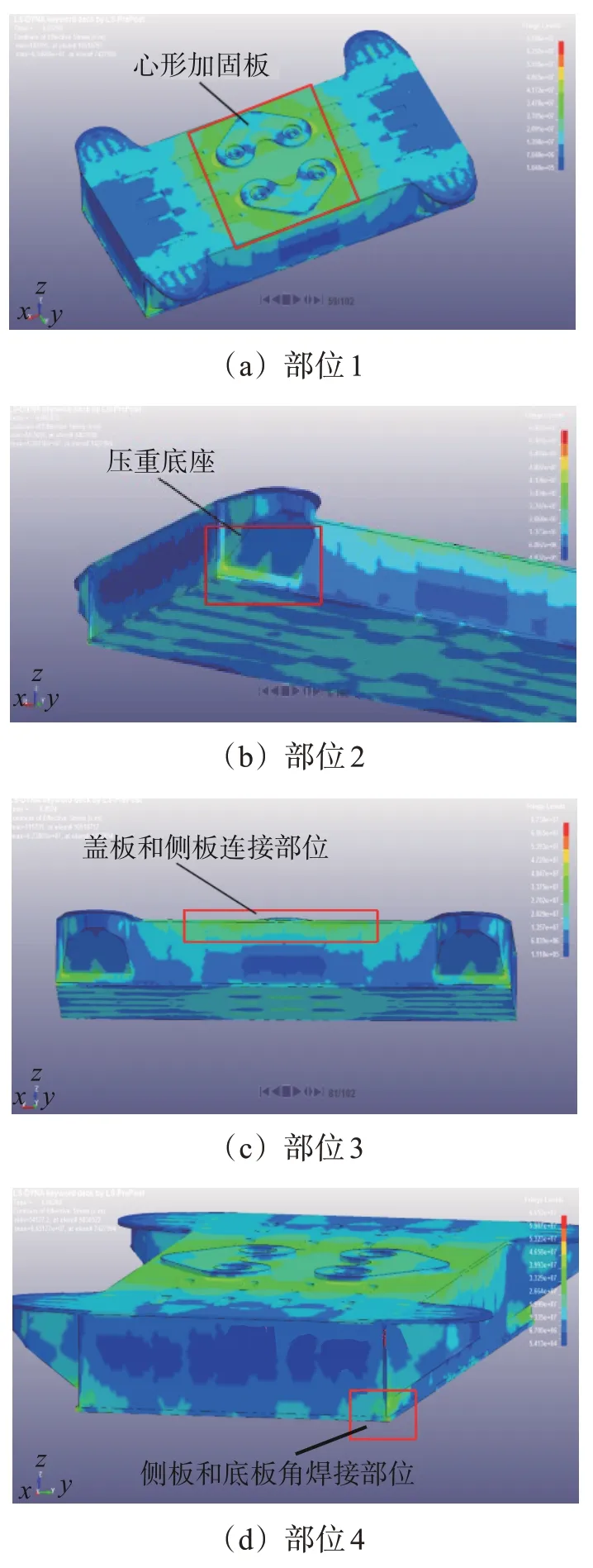
图3 平板的疲劳关键部位Fig.3 Key fatigue parts of baseplate

1.4.2 平板疲劳关键部位应力分析

在9种参数组合下，振动器平板疲劳关键部位的等效应力如图4所示。由图可知，平板关键疲劳部位1的等效应力峰值最大，是最容易产生疲劳损伤的部位。

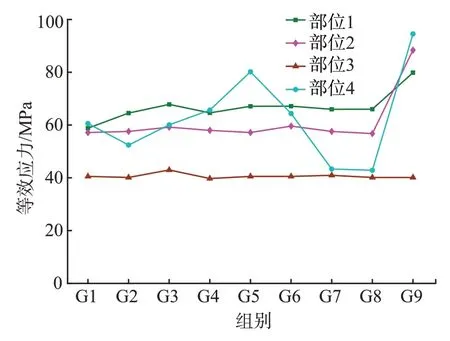
图4 平板疲劳关键部位等效应力对比Fig.4 Comparison of equivalent stress of key fatigue parts of baseplate

1.5 平板疲劳关键部位热点应力响应函数的确定

1.5.1 热点应力响应函数的建立

振动器平板的热点应力一般位于焊趾表面［15］。为此，根据线性外推法理论，分析距离焊趾0.5t～1.5t（t为平板厚度）范围内平板的热点应力，并运用多元非线性函数模型拟合得到平板疲劳关键部位的热点应力与各输入变量（活塞杆端面面积A、下十字柱直径D和交变液压力峰值P）之间的函数关系：

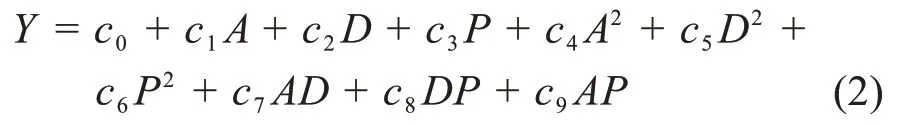
式中：c0至c9为常数。

1.5.2 热点应力响应函数系数的确定

根据基于三因素三水平正交试验表设计的方案，通过仿真分析得到振动器平板疲劳关键部位的热点应力峰值与活塞杆端面面积A、下十字柱直径D和交变液压力峰值P之间的关系，并求解得到热点应力响应函数中各系数的值，如表2所示。

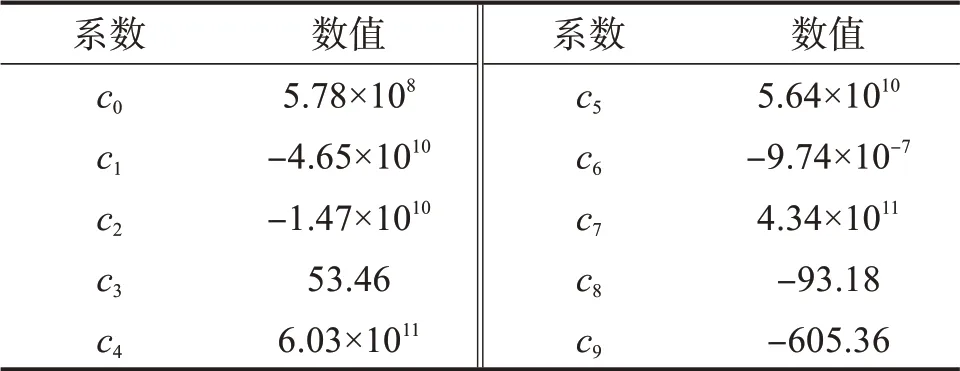
表2 平板疲劳关键部位热点应力响应函数的拟合系数Table 2 Fitting coefficient of hot spot stress response function of key fatigue parts of baseplate

2 复杂工况下振动器平板的疲劳寿命预测

针对振动器平板在复杂工况下的疲劳失效问题，采用S—N曲线法和断裂力学法来预测平板在复杂工况下的疲劳寿命。

2.1 基于S—N曲线法的疲劳寿命预测

2.1.1 平板试件的S—N曲线拟合

S—N曲线是表征构件最大应力S与循环次数N关系的曲线。在双对数坐标系中，S与N通常呈线性关系，即：

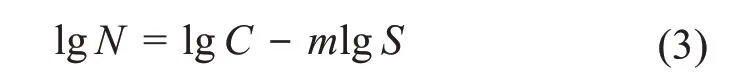
式中：C、m为构件的材料常数。

本文研究的平板试件的材料为45钢，由文献［16］可知，在常温条件下m=7.314 4。结合MTS-810疲劳试验机的加载结果，利用式（3）反推得到C，从而确定平板试件的S—N曲线：

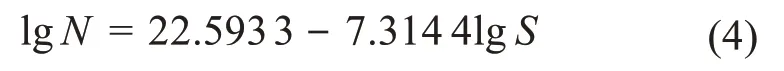
2.1.2 平板试件的S—N曲线修正

通常情况下，构件的S—N曲线很难通过实验方法来获取。因此，本文采用特征试件的S—N曲线［17］来修正平板的S—N曲线，为：

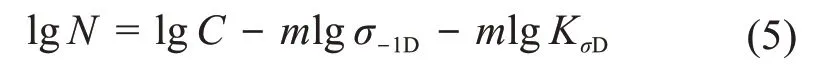
式中：σ-1D为平板的对称循环应力幅；KσD为修正系数，由平板的尺寸、粗糙度和应力集中系数决定，本文取KσD=1.332［18］。

修正前后平板试件的S—N曲线如图5所示。

图5 修正前后平板试件的S—N曲线对比Fig.5 Comparison of S-N curves of baseplate speci‐men before and after correction

2.1.3 基于S—N曲线法的平板疲劳寿命预测模型

首先，利用Goodman理论对平板疲劳关键部位的各级应力进行简化处理，得到应力水平函数N=h(S)；然后，结合热点应力响应函数，基于Palmgren-Miner累积损伤准则，运用S—N曲线法建立以振动器的结构、载荷参数（A、D、P）及其平板的材料参数（抗拉强度Su）为变量的平板疲劳寿命预测模型：

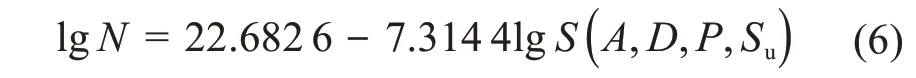
基于式（6）可得平板的疲劳寿命随振动器的结构、载荷和材料参数（A、D、P和Su）的变化规律，如图6所示。

图6 平板疲劳寿命随振动器的结构、载荷和材料参数的变化规律Fig.6 Variation of baseplate fatigue life with structure,load and material parameters of vibrator

2.2 基于断裂力学法的疲劳寿命预测

振动器平板在加工制造过程中会出现非常细小的气孔、夹渣和裂纹。在外载作用下，裂纹会不断扩展，直至平板断裂失效，因此可采用断裂力学法来构建平板的疲劳寿命预测模型。

影响平板疲劳裂纹扩展的主要因素包括初始裂纹尺寸a0、临界裂纹尺寸ac、材料常数E和h、形状参数Ys、材料断裂韧度Kc、应力比R和应力变程Δσ。运用Paris和Forman裂纹扩展理论，建立基于断裂力学法的平板疲劳寿命预测模型：

由式（7）可知，平板的疲劳寿命与疲劳裂纹扩展的影响因素（a0，ac，R，Δσ）直接相关，其随各参数的变化规律如图7所示。

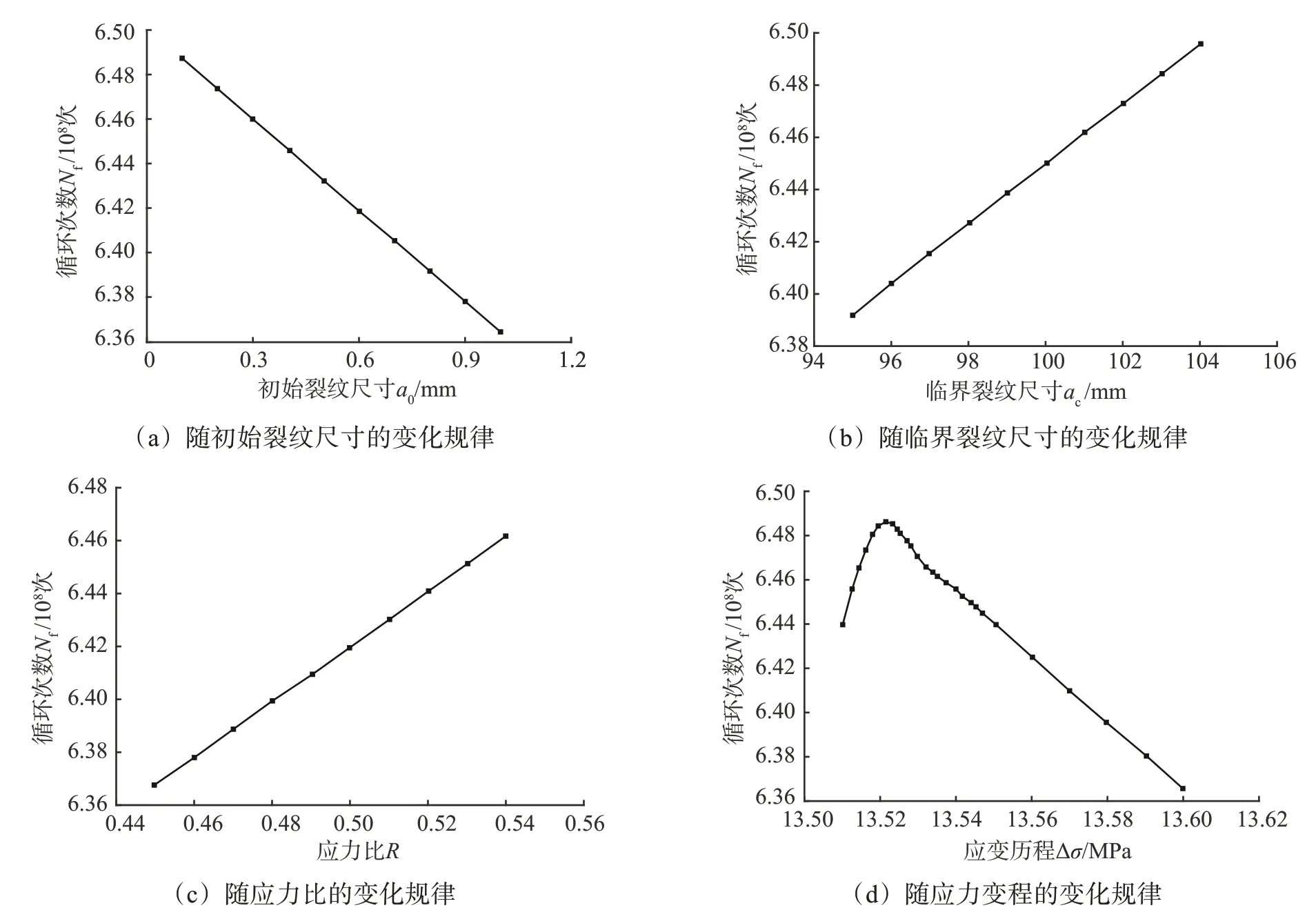
图7 平板疲劳寿命随疲劳裂纹扩展的影响因素的变化规律Fig.7 Variation of baseplate fatigue life with influence factors of fatigue crack propagation

3 传统的振动器平板疲劳可靠性分析方法

传统的疲劳可靠性分析是基于S—N曲线法和断裂力学法单独展开的，其中S—N曲线法是基于振动器的结构、载荷和材料参数（A、D、P和Su），即从宏观角度开展疲劳可靠性评估的，而断裂力学法是基于平板疲劳裂纹扩展的影响因素（a0、ac、R、Δσ），即从微观角度开展疲劳可靠性评估的。

3.1 基于S—N曲线法的平板疲劳可靠性分析

根据基于S—N曲线法的平板疲劳寿命预测模型，建立平板的极限状态函数，并结合Monte-Carlo（蒙特卡洛）法，求得平板的4个疲劳关键部位的可靠性。

3.1.1 平板疲劳可靠性计算参数确定

由于平板疲劳关键部位的热点应力响应曲线在1 个周期内是单峰值曲线，故基于S—N曲线的平板疲劳寿命预测模型可表示为：

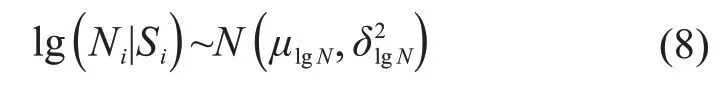
其中：

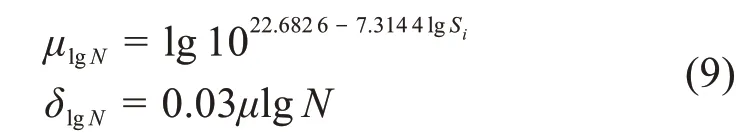
式中：μlgN、δlgN分别为均值和方差。

本文通过实验获取振动器的结构、载荷和材料参数的分布类型和取值，如表3所示。

表3 振动器的结构、载荷和材料参数的分布类型和取值Table 3 Distribution types and values of structure,load and material parameters of vibrator

3.1.2 基于S—N曲线法的极限状态函数确定

基于S—N曲线法的平板疲劳寿命预测模型中共有4个随机变量（A、D、P和Su），则平板疲劳寿命的极限状态方程可以表示为：

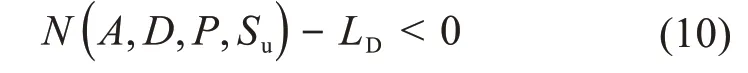
式中：LD为平板的设计寿命，根据现场统计资料，在激振力作用下平板承受2.0×108次循环激励后发生开裂现象，则本文取LD=2.0×108次。

3.1.3 基于S—N曲线法的平板疲劳失效概率计算

对平板的4个疲劳关键部位的失效概率进行计算。利用Monte-Carlo 法，生成n个独立随机变量样本N(A，D，P，Su)，然后通过计算机进行抽样，并统计实际寿命未达到设计寿命的样本数，计算其与总样本数量的比值，由此得到平板的4个疲劳关键部位的失效概率，如图8所示。

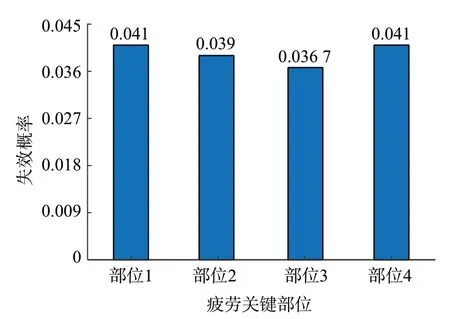
图8 基于S—N曲线法的平板疲劳关键部位的失效概率Fig.8 Failure probability of key fatigue parts of baseplate based on S-N curve method

3.2 基于断裂力学法的平板疲劳可靠性分析

根据基于断裂力学法的平板疲劳寿命预测模型，建立其极限状态函数，并结合Monte-Carlo法，求得平板疲劳关键部位的可靠性。

3.2.1 平板疲劳裂纹扩展的影响因素的分布类型确定

根据平板疲劳裂纹扩展的影响因素，本文通过实验来确定其分布类型和取值，如表4所示。

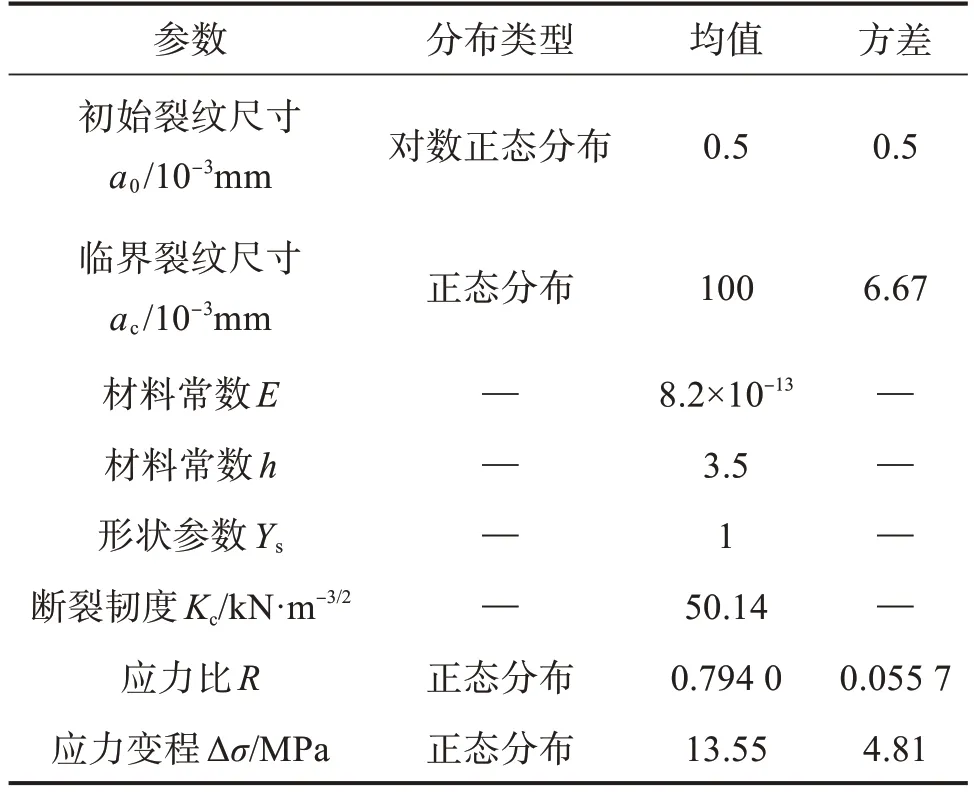
表4 疲劳裂纹扩展的影响因素的分布类型和取值Table 4 Distribution types and values of influence factors of fatigue crack propagation

3.2.2 基于断裂力学法的极限状态函数确定

基于断裂力学法的平板疲劳寿命预测模型中共有4个随机变量（a0，ac，R，Δσ），则平板疲劳寿命的极限状态函数可表示为：

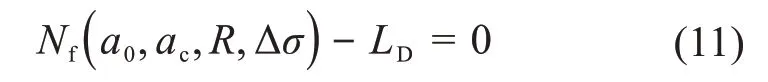
3.2.3 基于断裂力学法的平板疲劳失效概率计算

对于基于断裂力学法的平板疲劳可靠性分析，仍采用Monte-Carlo法来计算平板的4个疲劳关键部位的失效概率，如图9所示。

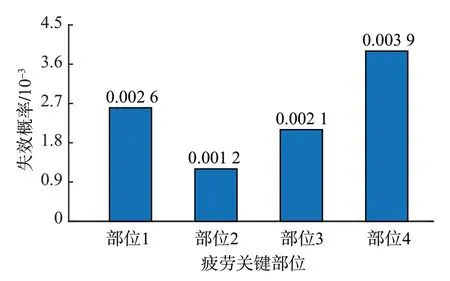
图9 基于断裂力学法的平板疲劳关键部位的失效概率Fig.9 Failure probability of key fatigue parts of baseplate based on fracture mechanics method

4 基于模糊综合评价法的振动器平板疲劳可靠性分析

由上文分析结果可知，2种疲劳寿命预测模型均具有一定的精度，但平板疲劳失效不仅与振动器的结构、载荷和材料参数有关，还与疲劳裂纹扩展的影响因素有关，故单一的疲劳寿命预测模型很难准确地预测平板在复杂工况下的疲劳寿命。为此，提出一种平板疲劳可靠性模糊综合分析模型，即结合S—N曲线法和断裂力学法的优势，找到一种可准确分析平板疲劳可靠性的方法。

4.1 建立因素集

从计算的精确性、分析效率、稳定性、适用性、便捷性和分析成本等多个方面考虑，构建平板疲劳可靠性模糊综合分析的因素集：

4.2 建立权重矩阵

考虑上述因素集中各因素的影响，由专家对各因素进行打分，以此建立平板疲劳可靠性影响因素的权重矩阵C：

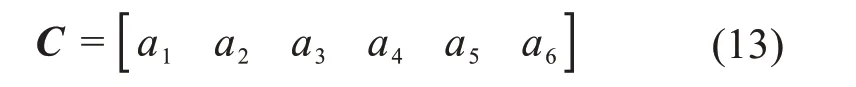
式中：ak为权重系数，满足。

在本文中，权重矩阵C=［0.2 0.1 0.2 0.2 0.1 0.2］。

4.3 建立模糊矩阵

根据每个因素的影响，对基于S—N曲线法和断裂力学法的2 种平板疲劳可靠性分析模型的隶属度进行计算，得到平板疲劳可靠性分析的模糊矩阵Z：

4.4 建立模糊综合评价矩阵

根据模糊综合评价矩阵B与权重矩阵C和模糊矩阵Z的关系，结合5 位专家打分的情况，计算得到平板疲劳可靠性的模糊综合评价矩阵B为：

则平板疲劳可靠性的模糊综合平均评价矩阵B1=[0.70184 0.732 84]。

4.5 疲劳可靠性模糊综合评价

基于权重分配原则，对基于S—N曲线法和断裂力学法的2种疲劳可靠性分析模型进行加权处理，其中权重系数须满足：

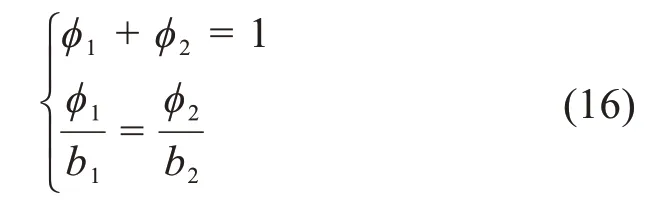
式中：ϕ1、ϕ2为模糊权重系数；b1、b2为模糊评价参数。

通过上述条件可得，基于S—N曲线法的平板疲劳可靠性分析模型的权重系数ϕ1=0.49174，基于断裂力学法的平板疲劳可靠性分析模型的权重系数ϕ2=0.508 26，则可得平板疲劳可靠性的模糊综合分析模型为：

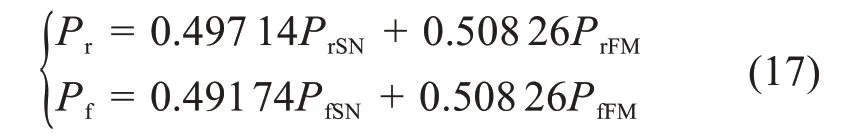
式中：Pr、Pf分别为基于模糊综合分析法计算的平板疲劳可靠度和失效概率；PrSN、PfSN分别为基于S—N曲线法计算的平板疲劳可靠度和失效概率；PrFM、PfFM分别为基于断裂力学法计算的平板疲劳可靠度和失效概率。

以平板的疲劳关键部位1为例，对比由基于3种疲劳可靠性分析方法计算得到的平板疲劳可靠度和失效概率，如表5所示。

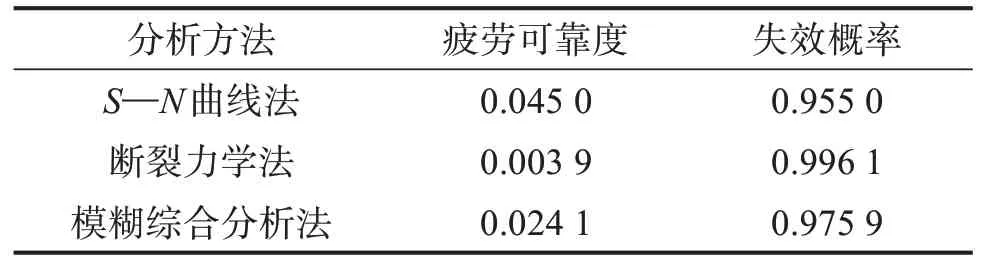
表5 基于3种疲劳可靠性分析方法的平板疲劳可靠度和失效概率对比Table 5 Comparison of fatigue reliability and failure prob‐ability of baseplate based on three fatigue reliabil‐ity analysis methods

5 振动器平板的疲劳可靠性优化设计

基于平板的疲劳可靠性模糊综合分析模型，以振动器的结构、载荷和材料参数（A、D、P和Su）以及疲劳裂纹扩展的影响因素（a0、ac、R和Δσ）为随机变量，对平板的疲劳可靠性进行优化设计，优化流程如图10所示。

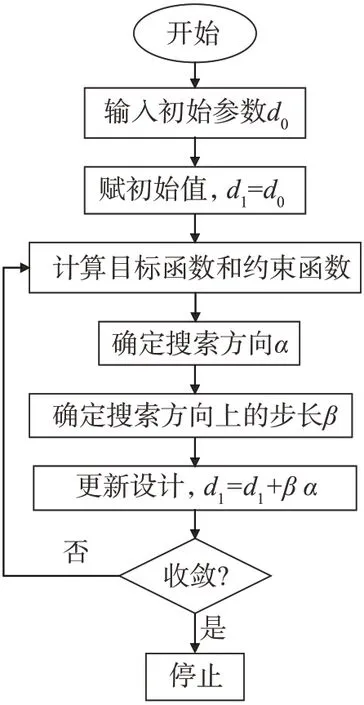
图10 平板疲劳可靠性优化设计流程Fig.10 Optimization design process of baseplate fatigue reliability

5.1 基于S—N曲线法的平板可靠性优化设计

由上文分析可知，在平板工作过程中，振动器的结构、载荷和材料参数（A、D、P和Su）对其疲劳寿命有重要影响。根据基于S—N曲线法的平板疲劳寿命预测模型，建立相应的约束函数：

其中：

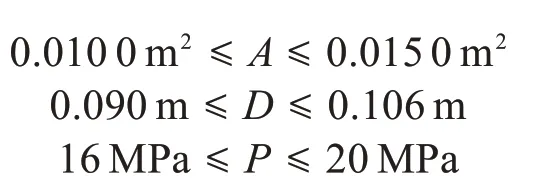
以平板疲劳部位的失效概率为约束条件，优化设计变量d=(A，D，P)，结合优化目标（失效概率小于0.010）和约束函数，建立基于S—N曲线法的平板疲劳可靠性优化模型：

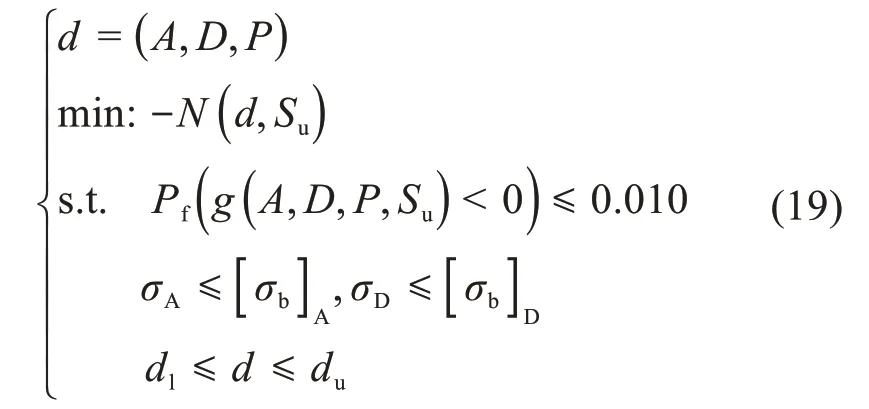
基于平板的最危险部位（疲劳部位1），从疲劳失效概率为0.045开始，逐步提高优化要求，分别取Pf=0.045，0.043，0.040，0.035，0.030，0.026，0.022，0.016，00.012，0.010，0.008，以此为约束条件，对振动器参数进行优化设计，从而优化平板的疲劳可靠性，结果如图11和图12所示。

由图11和图12可知：随着平板疲劳失效概率约束值的减小，振动器的结构、载荷参数（A、D、P）均减小；当平板的疲劳失效概率约束值减小为0.010 时，疲劳寿命曲线出现拐点，此时平板的疲劳可靠度达0.990 0，故振动器的最佳结构、载荷参数为：A=0.092 m2，D=0.011m，P=16.33MPa。

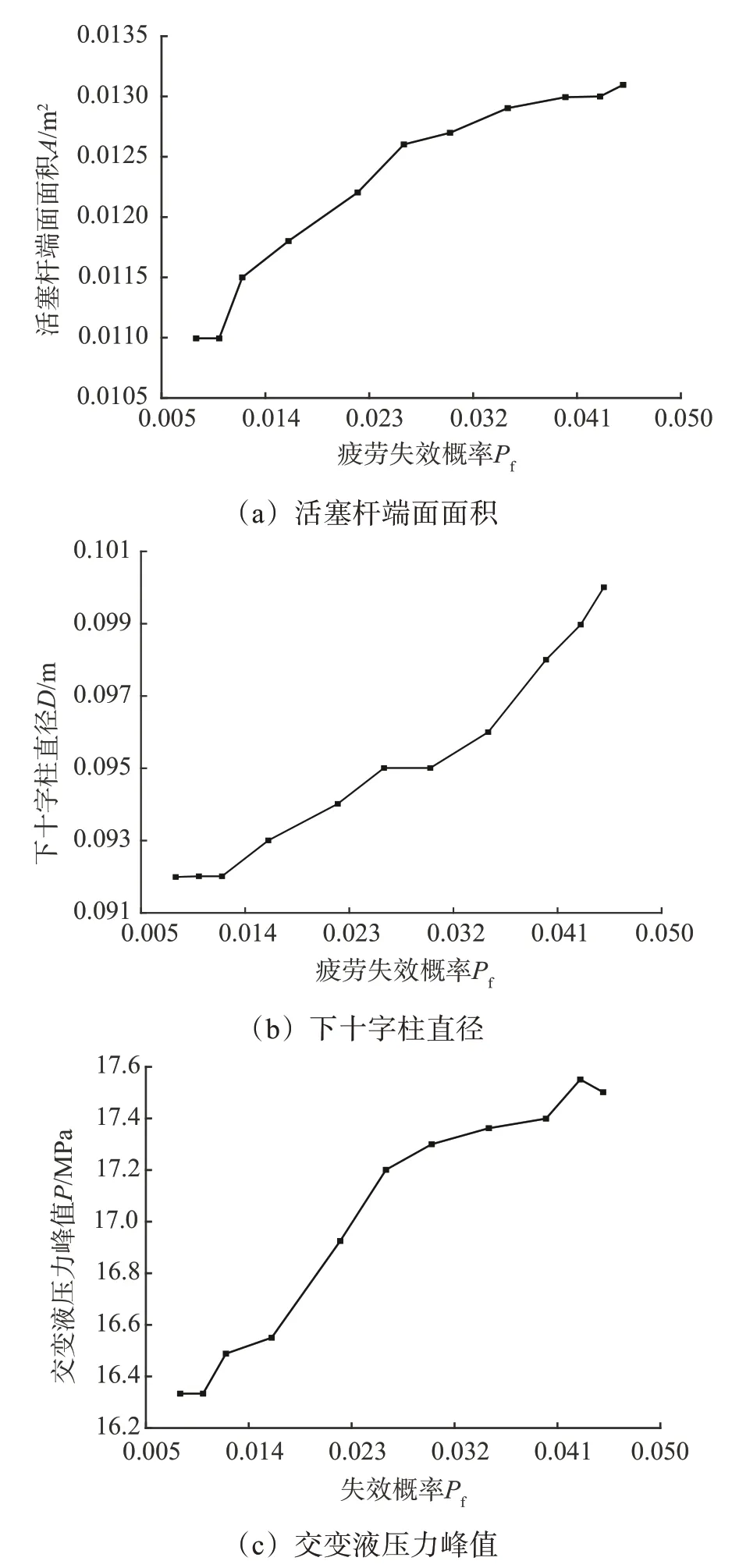
图11 基于S—N曲线法的振动器参数优化结果Fig.11 Optimization results of vibrator parameters based on S-N curve method

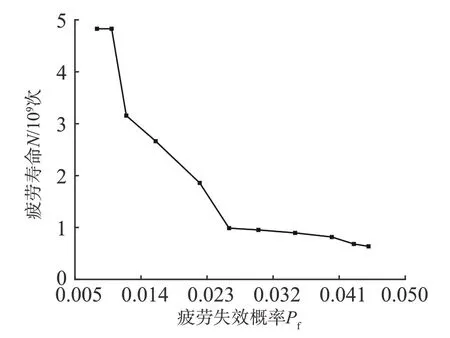
图12 基于S—N曲线法的平板疲劳寿命优化结果Fig.12 Optimization results of baseplate fatigue life based on S-N curve method

5.2 基于断裂力学法的平板疲劳可靠性优化设计

以Δσ、a0、ac、R为设计变量，建立约束函数h(d)=Nf-LD（其中0.1mm ≤a0≤1mm；95 mm ≤ac≤104 mm，0.6≤R≤0.95，0 MPa ≤Δσ≤13.6 MPa），以保证目标函数Nf(a0，ac，R，Δσ)取得最大值，由此得到基于断裂力学法的平板疲劳可靠性优化模型：

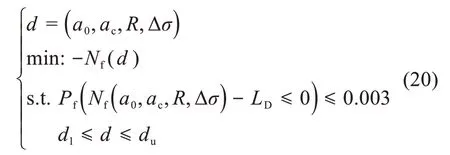
同样基于平板的最危险部位（疲劳部位1），从失效概率0.003 9 开始，逐步提高优化要求。取Pf=0.039 0，0.003 8，0.003 7，0.003 6，0.003 5，0.003 4，0.003 3，0.003 2，0.003 1，0.003 0，0.002 9 和0.002 8，以此为约束条件，对疲劳裂纹扩展的影响因素进行优化设计，从而优化平板的疲劳可靠性，结果如图13和图14所示。

由图13和图14可知：随着平板疲劳失效概率约束值的减小，a0和Δσ均减小，而ac和R增大；当疲劳失效概率约束值减小为0.003 0时，平板的疲劳寿命曲线出现拐点，此时疲劳可靠度达到0.997 0，则疲劳裂纹扩展的影响因素的最佳值为：a0=0.21mm，ac=103mm，R=0.93，Δσ=13.06 MPa。

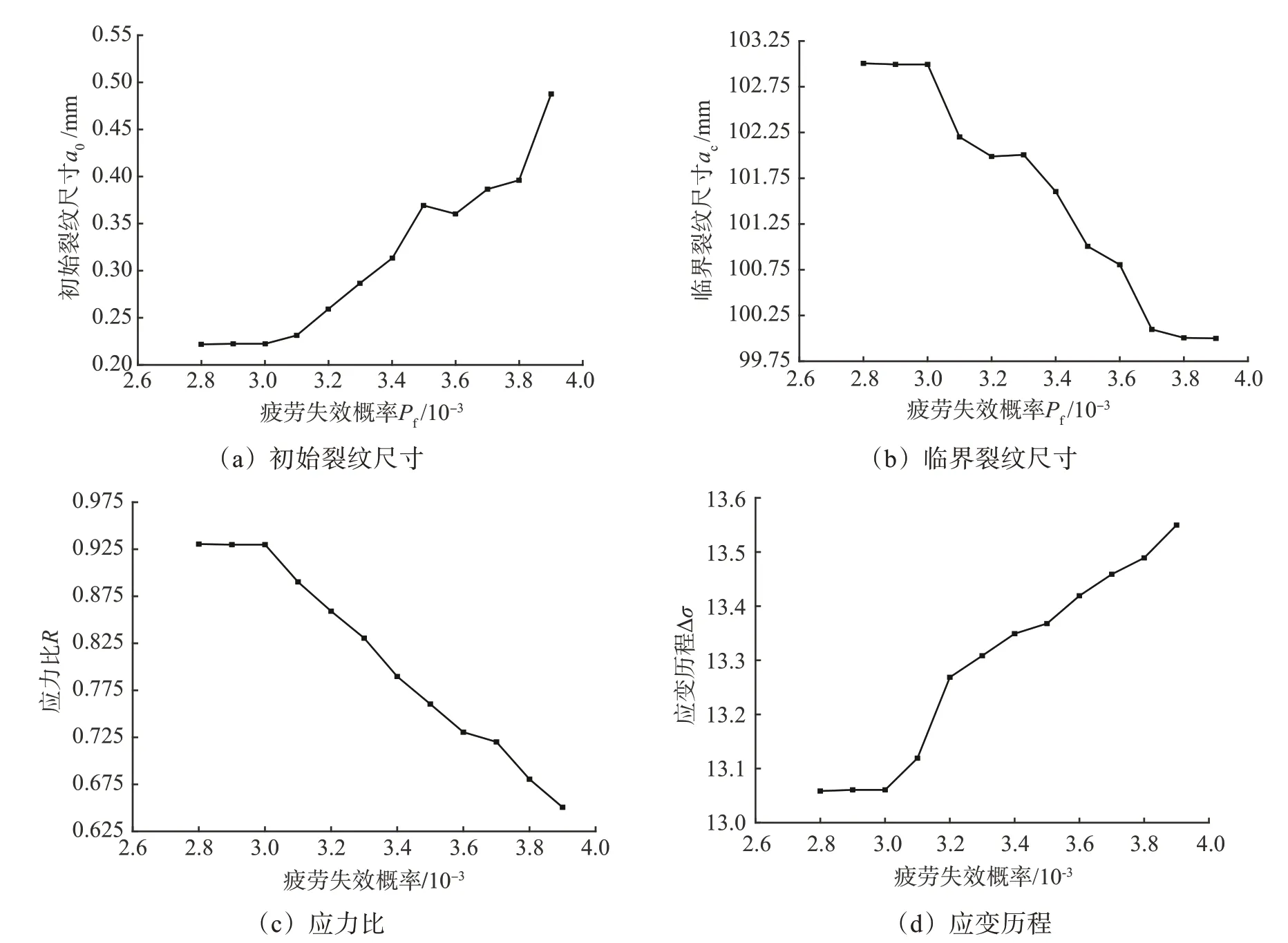
图13 基于断裂力学法的疲劳裂纹扩展的影响因素的优化结果Fig.13 Optimization results of influence factors of fatigue crack propagation based on fracture mechanics method

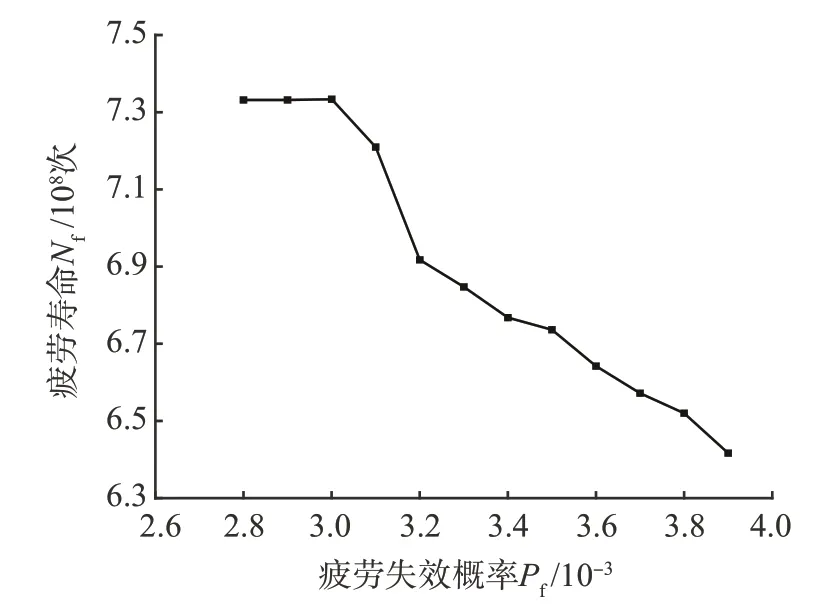
图14 基于断裂力学法的平板疲劳寿命优化结果Fig.14 Optimization results of baseplate fatigue life based on fracture mechanics method

综上，通过分别基于S—N曲线法和断裂力学法对平板的疲劳可靠性进行优化设计后，平板的疲劳可靠度分别达到0.990 0和0.997 0，将其代入式（17）可得平板的综合疲劳可靠度为0.993 5，相比优化前提高了1.8%。

6 结论

1）根据平板的动力学分析结果，确定了平板的4个疲劳关键部位，并建立了疲劳关键部位的热点应力响应函数。

2）利用平板的特征试件，建立了基于S—N曲线法的平板疲劳寿命预测模型。同时运用Paris和Forman裂纹扩展理论，建立了基于断裂力学法的平板疲劳寿命预测模型。结合2种疲劳寿命预测模型对应的极限状态函数，运用Monte-Carlo法，得到4个关键部位的疲劳可靠性。并依据模糊综合评价法定量分析了S—N曲线法和断裂力学法的权重系数，构建了平板疲劳可靠性模糊综合分析模型。

3）利用S—N曲线法对振动器的结构、载荷参数进行优化，结果表明，当A=0.092 m2，D=0.011m，P=16.33MPa时，平板的疲劳可靠度为0.990 0。利用断裂力学法对疲劳裂纹扩展的影响因素进行优化，结果表明，当a0= 0.21mm，ac=103mm，R=0.93，Δσ=13.06 MPa时，平板的疲劳可靠度为0.997 0。基于平板疲劳可靠性模糊综合分析模型的计算可得，优化后平板的综合疲劳可靠度为0.993 5，相比优化前提高了1.8%。

基于模糊综合评价法的平板疲劳可靠性分析与优化方法综合考虑了振动器的结构、载荷和材料参数以及疲劳裂纹扩展的影响因素对平板疲劳可靠性的影响，具有较高的计算精度、稳定性和适用性。优化结果为可控震源振动器的结构、载荷参数的改进提供了工程指导建议，这对振动器平板抗疲劳性能的提高和使用寿命的延长具有重要意义。