快速成型技术中分段算法的研究综述
王春香,纪康辉,王 耀,刘 流
(内蒙古科技大学机械工程学院,内蒙古包头014000)
快速成型(rapid prototyping)是在现代CAD/CAM(computer aided design/computer aided manu‐facturing,计算机辅助设计/计算机辅助制造)技术、激光技术、计算机数控技术、精密伺服驱动技术以及新材料技术的基础上发展起来的新兴技术,其基本原理为“分层制造,逐层叠加”[1],可实现数字化模型到实体模型的转化。但在快速成型技术的实际应用中,存在几个较为突出的问题,如表1所示。

表1 分段算法应用情况Table 1 Application of segmentation algorithm
针对表1所示的情况,若直接进行等厚分层或自适应分层处理,则均无法得到较好的分层效果。为了更好地解决上述问题,引入分段算法。分段算法是表面分割算法的延伸。表面分割是指将模型表面分割为多个区域,而分段处理是对模型进行体分割,即基于由大变小的原则将完整的三维模型分割为多个子部分,将模型的整体成型转换为多个分块模型的成型与拼接。按照应用方法的不同,可将分段算法划分为多种类型。本文将从人机交互分段和自动分段(包括体素化分段、特征识别式分段、多目标优化分段和聚类式分段)两个方面对分段算法展开分析,对相关文献进行对比并对各分段算法的适用情况进行总结,旨在为快速成型技术的相关研究提供参考。
1 人机交互分段算法
对于在成型方向上有多个精度和粗糙度要求的待加工模型,在进行分层处理时,目前仍无法自动且准确地判断其分段界线,须人为地输入各个段块的边界位置,以完成分段处理。
Mani等[2]根据模型的几何形状和粗糙度要求,人为地设定了模型表面的分段位置,以进行人工干预分段。王春香等[3]从装配要求出发,考虑现有等厚分层算法的优势与不足,提出了按照成型方向上不同的精度要求,对具有装配要求的零件模型进行分段等厚分层的思想。Liu 等[4]基于给定的误差,将点云数据划分为多个区域。Li等[5]基于快速行进分水岭和标记控制的方法,提出了自动阈值设置和手动阈值调节相结合的方法以减少堆栈操作,克服了视觉直观分段控制中存在的困难,解决了可操作性差的问题,提高了分段质量及缩短了算法运行时间。
目前,主流的分层算法包括等厚分层算法和自适应分层算法,但这2种算法均无法兼顾成型精度和成型效率[1]。基于分段处理思想,结合等厚分层算法和自适应分层算法对模型进行划分,即先分段后分层,如图1所示[6]。但目前这种混合分层算法存在模型分段界线不明确和难以自动划分的问题,仍须采用人机交互方式,即人为地判定等厚分层算法或自适应分层算法的使用界限。Tyberg 等[7]提出了局部自适应思想,即先将模型细分为多个区域,再基于误差最小原则对每个区域进行自适应分层。Wang等[8]利用基于视觉显著性分段方法,手动地将模型划分为具有不同显著性的区域,并单独对每个区域进行自适应分层。

图1 模型的单一分层与基于分段的混合分层对比Fig.1 Comparison of single layering and mixed layer‐ing based on segmentation for model
应用分段算法也可将实体零件模型分为内、外两部分,鉴于内部永不可见,可采用比外部层厚大的层厚进行分层。Sabourin等[9]运用2种分层算法对模型内、外部分进行处理:外部精度要求高,采用较小层厚进行自适应分层;内部则采用较大层厚进行等厚分层,如图2所示[10]。Tyberg等[11]利用Stratasys公司的FDM1600 型快速成型机验证了文献[9]中分段算法的可行性,该分段算法可使零件模型的成型时间大幅缩短。
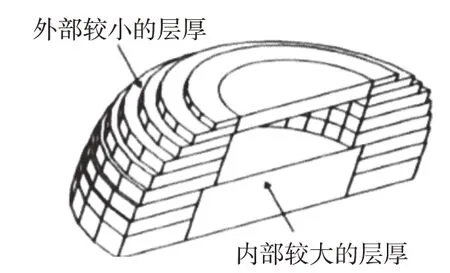
图2 基于内外分段的模型混合分层Fig.2 Hybrid layering of model based on inner and outer segmentation
然而,上述混合分层算法需要有专业人员通过人机交互方式来输入模型分段的边界位置。对于边界特征明显的模型,其段块界线易确定;但对于具有多曲率、多凹凸特征的模型,其段块界线较为模糊,不易精确划分且划分时要考虑后续制作过程,这对专业能力有要求,从而导致适用人群受到限制。
2 自动分段算法
针对人机交互分段算法在实际应用中存在局限的问题,国内外学者开展了关于自动分段算法的研究。自动分段是指在无人为干预的情况下直接得到准确的分段界线,自动地将整个模型划分为多个段块。本文将从体素化、特征识别和多目标优化等角度入手,以曲率、二面角等多个因素作为判断依据,结合区域生长、聚类等多种算法,对不同的自动分段算法进行分析和总结。
2.1 体素化分段算法
体素化(voxelization)是指将物体的几何表示形式转化成最接近该物体形状的体素形式。体素化分段是基于由大变小的原则,将一个整体模型转化成遵循同一划分规则的多个体素块模型。不同形状体素块的优缺点如表2所示。体素化分段可有效解决模型无法一次成型的问题,通过将模型划分成多个体素块,利用转换成型方向等方法,有效避免了支撑结构的存在。

表2 不同形状体素块的优缺点对比Table 2 Comparison of advantages and disadvantages of voxel blocks with different shapes
Hu等[12]和耿国华[13]将模型划分为类金字塔状体素块,如图3所示,前者将分段与ECP(exact cover problem,精确覆盖问题)相联系,并运用聚类方法推导得到一组类金字塔状的模型段块,相较于经典的凸分段算法[14],该方法产生的段块数量较少;后者根据FDM(fused deposition modeling,熔融沉积成型)工艺,提出了一种全局最优的模型分段与“打包”算法,将分段与“打包”加工相结合,以消耗的支撑材料和成型体积为约束条件,得到了一组模型分段的最优解。但是,Hu等采用的方法过度依赖于聚类方法,在理论上无法保证分段效果最优。魏潇然等[15]先采用区域生长算法对模型进行分区,并分析了各分区的多个候选划分方向,然后采用空间期望和椎体期望确定各个切分平面,将模型分成多个不需要支撑结构的椎体模型。虽然上述算法可将模型分段为类金字塔状和椎体形的体素块,减少或避免了因支撑而产生的材料消耗,便于模型的成型制作,但其并未考虑模型成型后的拼接问题。

图3 类金字塔状体素块Fig.3 Pyramid-like voxel block
为解决成型后的拼接问题,很多学者将模型划分为常规形状的体素块。Krause等[16]先将CAD模型分段成多个长方体体素块,然后分别对每个长方块进行切片分层,每一层的厚度取决于所需的表面粗糙度。Zhou等[17]采用连续折叠序列将三维模型转化为多个立方体体素块(如图4所示),各体素块之间可形成树形连接结构。Medellin等[18]和Chan等[19]采用规则分段和不规则分段相结合的方法对模型进行分段处理,对于规则分段,以圆柱体体素块和正方体体素块为基本单元;对于不规则分段,从实际装配要求出发,在接口处形成形状互补的凹陷/凸起结构。此外,上述文献也考虑了多个段块之间的光滑圆弧过渡连接结构,形成了单独的过渡块。

图4 立方体体素块Fig.4 Cube voxel block
2.2 特征识别式分段算法
特征识别式分段算法以二面角、特征环等为模型分段的判断依据,同时结合阈值、凹凸信号值等对模型进行特征识别,以找到分段的边界位置,实现模型的分段处理。结合实际应用情况,可形成多种特征识别式分段算法,该类算法可有效地解决成型范围过大和存在多个最优加工方向的模型的分段问题。
汤瑞清等[20]和Jiang 等[21]针对STL(stereolithog‐raphy,立体光刻)模型,提出了一种基于二面角的特征识别式分段算法,即通过比较相邻三角形的法向夹角与预设的角度阈值来识别STL模型的分段边界特征。王泽昊等[22]提出了一种基于凹凸信号最小值边界检测的三角网格模型分段算法,通过边界凹凸信号最小值的检测,实现了对三角网格模型分段边界特征的提取。上述特征识别式分段算法的优缺点如表3所示。

表3 不同特征识别式分段算法的优缺点对比Table 3 Comparison of advantages and disadvantages of different feature recognition segmentation algorithms
然而,上述算法中的模型大多为STL模型,存在因面片近似逼近模型表面而引起的分段边界线提取不准确的问题。为此,王会凤等[23]提出了基于特征的模型多目标优化分段算法,先采用基于图的特征识别方式[24]进行可加工性分析,再根据基于约束条件建立的目标函数对模型的最优分段面进行选取,并运用遗传算法进行多目标优化,从而完成模型的分段;Chiu等[25]基于识别得到的特征对模型凸出部分进行分段,将其划分为特征一致的小尺寸模型,该方法适用于具有悬臂特征的模型。
鉴于特征交汇处会形成特征环,可通过识别和重新构造特征环的方法来确定模型的分段边界线,从而实现模型的分段处理。Hao 等[26]通过提取特征边缘并构造特征环,基于合适的环路和节点将复杂的大尺寸模型划分为具有相似形状节点的简单小模型(如图5所示),该算法基于模型表面曲率进行分段处理,相比基于点和面的分段方式,其计算量大大减少;但是,虽可直接将特征环作为模型的分段边界线,但要求待分段模型表面具有显著特征,导致该算法的适用性并不强。对于结构较为简单的模型,可结合上述算法和体素化分段算法或矩阵划分算法进行模型分段处理。Kazemi等[27]运用交互循环方法和交互表面方法分别识别模型的特征,若识别的特征存在交集,则以该特征轮廓线作为分段边界线,对模型进行分段处理。纪小刚[28]基于三维模型与分层切平面相交形成的多个分段轮廓线,利用三角形网格对相邻的分段轮廓线进行填充,并在分段处加入空间封闭面,从而完成模型的分段处理。

图5 基于特征环的模型分段Fig.5 Model segmentation based on feature loop
2.3 多目标优化分段算法
多目标优化分段算法是从实际成型应用的影响因素入手,先建立打分评价机制,构建各影响因素的约束条件,再以各影响因素作为目标函数中的变量并对其赋予相应的权重,由此将模型分段问题转化为目标函数最优解求解问题。这类多目标优化分段算法可有效解决成型尺寸过大且无法一次成型的模型的分段问题。
Yao等[29]提出了6个模型分段质量评价指标:应力负载、表面细节、界面面积、包装大小、可打印性和组装性,并采用层次集方法将这6个评价指标集成到1个分段边界线寻优算法中,重复进行局部多目标优化,直至找到最优的模型分段边界线,如图6所示。相比于基于网格和粒子的表示方法,基于层次集的表示方法能更加灵活地处理模型多目标优化分段问题。Oh 等[30]从加工时间、加工成本和表面粗糙度这3 个因素出发,对模型进行区域划分,再将划分后的模型按最优加工方向进行加工。Cheng 等[31]将零件成型精度、打印时间和稳定性作为评价指标,在将实体模型的表面划分为不同类型的子表面后,对每个子表面赋予相应的权重,以确定最优的分段结果,并完成模型的优化分段。该算法不仅适用于平面、圆柱面类模型,也适用于复杂曲面类模型,适用范围较为广泛。

图6 基于层次集方法的模型分段Fig.6 Model segmentation based on hierarchical set method
然而,上述3种分段算法均以多个因素作为模型分段目标函数的约束条件,但均未考虑段块的后续拼接问题。考虑到段块单独成型后须拼接为整体,则应在分段时预留连接位置,以便于后续拼接。Lau等[32]提出了一种预留螺钉连接口的多目标优化分段算法,通过在对家具模型分段时预留螺钉连接口的方式,实现了各零部件模型单独打印成型后的后续装配。Xin等[33]基于鲁班锁的构造原理,将模型分段为连接件和被连接件两部分,连接件部分采用鲁班锁连接结构形式,如图7所示,该连接结构不需要粘结剂且稳定性很高。Wang等[34]从优化打印方向的角度来提高各模型段块的表面打印质量,并在段块切面上设计了连接器,以便分段模型成型后的手工组装和拆卸,如图8所示。
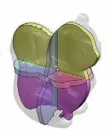
图7 鲁班锁连接结构Fig.7 Luban lock connection structure
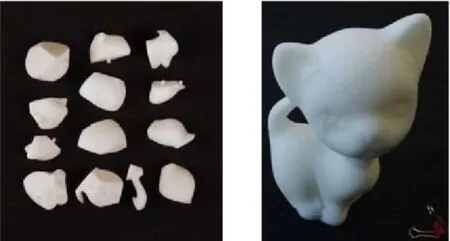
图8 基于预留连接器的模型组装Fig.8 Model assembly based on reserved connector
在对模型进行分段时,还须考虑段块的数量。Luo 等[35]提出了“Chopper”框架,并制定了一些理想划分的评价指标,包括可装配性、分块数量、可打印性、美观性和结构稳定性,并建立相应的目标函数,采用定向搜素(beam search)优化方式逐步构建最优的BSP(binary space partitioning,二叉空间分割)树,并通过用户指导生成模型段块,如图9所示。该方法对分段约束的选择和目标函数的建立有很大的参考价值,但未将打印材料的选择和支撑结构的构建纳入优化体系。

图9 基于“Chopper”框架的模型分段Fig.9 Model segmentation based on‘Chopper’frame
2.4 聚类式分段算法
聚类分析是目前最常用的数据分析处理技术之一,其通过簇划分使数据集形成若干个性质相似的聚类,属于无监督的机器学习方法[36]。在模型分段过程中,较常使用自适应谱聚类、迭代聚类和层次聚类等算法。在很多情况下,常通过结合聚类算法和其他算法来实现模型的自动分段。聚类式分段算法可有效解决存在多个最优加工方向的模型的分段问题。
石晨晨[37]为了将三角网格聚类成单元,引入了打印方向这一对成型质量至关重要的因素,并采用投票的方法对每个打印方向上的三角网格进行投票,将打印方向相同的三角网格聚类成一个单元;形成聚类单元后,对所有打印方向上的聚类单元进行相似度测量,形成聚类单元之间的相似度矩阵,并以此作为谱聚类的依据来对单元进行分块,从而完成STL 模型表面的分割;最后采用SVM(support vector machine,支持向量机)算法生成相邻块之间的切割平面,从而完成STL模型的分段,效果如图10所示。该算法极大地提高了加工效率,但受限于加工效率和支撑材料的消耗。对于复杂模型,采用该算法分段时产生的段块较少,不利于后续拼接,而且段块少不但不能提高加工效率,反而会延长加工时间。

图10 基于聚类算法的模型分段Fig.10 Model segmentation based on clustering algorithm
模型分段问题也可以转化为关键节点划分问题,即先找到可表征模型特征的关键节点,再根据相关判据进行段块划分。高天一等[38]利用平均曲率骨架方法[39]对点云模型进行骨架提取,并根据骨架之间的关系选择关键节点,然后选择同一领域内距离质心最近的点作为最终的关键节点,并以此关键节点作为改进区域生长算法的种子,从而完成点云模型的分段处理。但是,上述算法未保留点云和三角面片的关联关系,会造成可视化过程中分段边界线不光滑的问题。Jiang 等[40]采用PCA(principal component analy‐sis,主成分分析)方法将模型分段问题从三维转化为二维,即先运用网格收缩方法将三维网格模型收缩成平面骨架模型,然后采用PCA 方法对骨架进行节点提取,并采用迭代聚类算法提取非节点,从而实现完整平面骨架模型的提取,最后利用遵循最小规则的空间扫描法将模型划分成多个段块,并考虑划分后段块的大小以及整个模型的对称性、过渡约束和可装配性,运用贪婪算法进行调整划分,最终完成模型的分段处理,如图11所示。但该算法不适用于缺乏明显凹陷特征的模型,且未考虑最优加工方向和支撑材料的问题。Hildebrand 等[41]通过法线层次聚类算法寻优得到一组最优的正交基,并按这3个正交方向对模型进行分段。相较于传统的PCA 方法,基于该算法产生的段块的体积误差较小,但计算量较大且耗时较长。
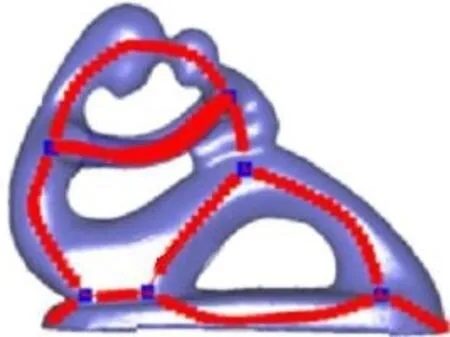
图11 基于节点提取的模型分段Fig.11 Model segmentation based on node extraction
3 结论与展望
本文总结了快速成型技术中的分段算法,从人机交互分段和自动分段两个方面展开分析,梳理了各分段算法的应用情况及优缺点,旨在为后续的分层处理提供参考,结论和展望如下。
1)综合国内外研究现状可知,尽管现有分段算法众多且面向不同成型模型,但其适用范围仍然有限,且缺乏系统的分段效果评价标准。
2)在快速成型制造中,人机交互式分段算法得到了实际应用,且成型工艺类型多为FDM及光固化。而自动分段算法仅限于仿真模拟,在实际成型制造中的应用仍有待研究。
3)目前仅少数分段算法考虑了模型分段后的拼接问题,但拼接类型仍有待进一步研究。此外,分段时预留的装配接口须考虑模型的性能及可行性。
4)现有分段算法的应用对象多为斯坦福兔子等非工程用模型,针对工程应用领域的零部件(如斗齿、链轨节)模型等的分段技术仍不成熟。未来可结合相关理论,拓宽分段处理在机械工程领域的应用范围。

