水下机械手动力学研究综述
刘晓瑜,田 颖,张明路
(河北工业大学机械工程学院,天津300132)
地球表面约75%的面积被海洋所覆盖,我国的海洋面积约为陆地面积的1/3。海洋中蕴藏着丰富的生物、能源和矿产资源,但目前我国海洋开发事业的发展相对缓慢。近年来,随着海洋资源开发和海洋科学研究的不断深入,对水下机器人的需求大幅提升。
水下机器人是一种能在水中浮游或行走的机械装置,机械手是大部分水下机器人的重要组成部分。例如:对于常见的复杂水下采集作业,水下机器人在缺乏机械手时根本无法完成。准确的动力学分析是水下机械手精确、高效地完成作业的前提。因此,对水下机械手进行动力学分析具有重要的理论意义和工程价值。
为此,针对水下机械手动力学的研究方法与技术,笔者对其进行分析总结,主要包括:1)现有水下机械手的功能和设计特征;2)基于误差补偿的水下机械手动力学建模方法以及基于水动力学模型的水下机械手动力学建模方法;3)惯性及黏性水动力学模型构建方法。通过对比不同的水下机械手动力学研究方法,旨在探究现有研究方法的不足并提出未来可研究的新方向。
1 水下机械手的功能和设计特征
水下机械手是最适合用于执行海底作业的工具,可用于海底石油和天然气的勘测等。水下机械手多搭载于移动平台,如载人航行器(human occupied vehicle,HOV)、远程遥控航行器(remotely operated vehicle,ROV)和自主水下航行器(autonomous under‐water vehicle,AUV)等[1-2]。通常情况下,这些移动平台均配有1个或多个水下机械手。
水下机械手常用于辅助人类执行各种难以完成的任务。Zhang 等[3]开发了一种深海主从液压机械手(如图1所示),可通过远程操作来测量海下7 000 m处的压力。Chang等[4]为辅助水下施工作业,设计了一种可远程遥控的水下机械手系统,其配有距离测量系统,可提供水下物体的准确位置信息,从而快速又准确地完成水下作业。Jones[5]通过远程操作水下机械手来完成深水环境下的样品收集,以对水下生态环境进行评估,从而为人类提供用于改善水下生态环境的数据。Bowen等[6]开发了一种新颖的水下航行器,其机械手上装有摄像头和声呐,可通过远程遥控操作来探索海下11 000 m处的生态环境,实现对深海环境的科学调查。Ribas等[7]基于自主设计的水下研究平台Girona 500,开展了多种水下机械手的设计,通过在平台上配置多种机械手来完成勘测和干预等不同形式的水下任务。此外,他们还研发了一种可完全自主执行水下任务的介入式AUV(简称为I-AUV,如图2所示),该AUV配备了七自由度电动机械臂(装有三指式抓爪),可通过自由浮动模式来完成水下作业。

图1 深海主从液压机械手Fig.1 Deep sea master-slave hydraulic manipulator

图2 I-AUV的水下机械手Fig.2 Underwater manipulator for I-AUV
针对水下机械手的研究包含机械手的结构设计、静/动力学分析、运动轨迹规划以及末端执行器与外部传感器配置等多个方面。Siciliano等[8]分析了不同类型的机械手,详细介绍了机械手的设计理论、动力学推导过程以及运动控制算法。考虑到水下机械手与陆上机械手的工作环境存在差异,Pal 等[9]对多种不同类型的水下机械手与陆上机械手进行了分析,讨论了两者在运动学、动力学以及控制方面的不同之处,旨在为水下机械手的设计提供参考。
水下机械手的控制系统是其重要的组成部分,其设计十分关键。Marani等[10]研制了一款用于干预任务的半自主水下航行器(semi autonomous under‐water vehicle for intervention mission,SAUVIM),其自动操纵控制系统具有强鲁棒性,使得其末端的机械手能够可靠地用电缆将目标钩住并拉至水面。但是,由于机械手与水下航行器之间的相互作用会影响机械手的作业精度,使得机械手与水下航行器的控制系统较为复杂。对此,Antonelli等[11]提出了一种配备七自由度机械手的水下航行器的动态控制方案,该方案采用自适应方法和递归方法,假定机械手各关节串联并采用独立控制方式,从而抵消了机械手引起的动态相互作用,实现了考虑机械手的复杂控制系统的开发。水下机械手的控制性能在很大程度上决定着水下机器人的作业能力。不同于陆上机械手,水下机械手在运动中会受到由水产生的巨大阻力,这对其稳定运行及作业精度有较大干扰。因此,须对水下机械手的动力学模型进行分析,并设计相应的控制系统,以消除水环境的影响。
2 水下机械手的动力学建模方法
水下机械手作业时须基于稳定的控制策略,而构建准确的动力学模型是提升控制系统稳定性的前提[12-13]。根据机械手的动力学建模经验,采用牛顿欧拉法建立其动力学模型:

式中:τ为机械手各关节的理论力矩;M(q)为机械手各关节的惯性力矩;为机械手各关节的科氏力矩;为机械手各关节的重力矩;分别为机械手各关节的位置、速度和加速度。
完整的水下机械手动力学模型必须考虑水环境的影响[14-15],即水下机械手不仅要克服自身的重力和有效负载,还要克服水动力及其力矩。考虑水环境影响的水下机械手动力学模型为:
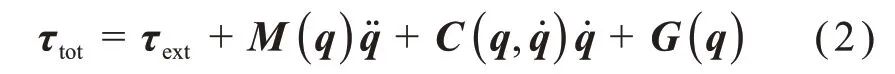
式中:τtot为水下机械手各关节所受的总力矩;τext为水环境产生的外力矩。
针对水下机械手作业时受到水环境的影响,目前主要采用以下2种方法来构建其动力学模型:基于误差补偿的动力学建模方法和基于水动力学模型的动力学建模方法。
2.1 基于误差补偿的动力学建模方法
水环境的影响导致传统的机械手动力学模型不够准确。因此,对于水下机械手各关节所受的力矩,传感器的测量值与基于传统动力学模型的计算值存在一定的误差,可表示为:

式中:τerror为水下机械手各关节所受力矩的误差;τsensor为水下机械手各关节所受力矩的测量值。
基于误差补偿的思想,可通过干扰力补偿、动态反馈调节和控制策略优化等方式来降低水环境的影响。
2.1.1 干扰力补偿
干扰力补偿是指将水下机械手受到的水作用力视为干扰力,通过补偿的方式来降低水环境的影响,从而使水下机械手可按预期要求工作。
李冀永等[16]以SY-II 水下机器人-机械手系统为对象,对机械手在水下作业时受到的干扰力进行了详细分析,并根据基于扰动力模型建立的动力学控制律设计了协调运动控制器,对影响机器人姿态的扰动力进行了估计和补偿。Soylu等[17]提出了一种与水下遥控航行器连接的六自由度空间机械手的动力学建模策略,在机械手受到干扰时重新调整控制力的大小,并通过数值模拟验证了该方案的有效性。Ishitsuka等[18]建立了水下机器人Twin-Burger的机械手的动力学模型,其将机械手视作二连杆刚性系统,因动态机械手与水环境之间存在相互作用,用1个简单的未知量来表示机械手在水下的额外受力,以补偿水流和其他外界环境的影响。
基于误差的干扰力补偿的前提是分析干扰力的状态[19],对分析结果的准确性要求较高,且分析方法没有固定思路,因此在动态多变的水环境中难以准确补偿干扰力,导致基于干扰力补偿的动力学建模方法的可移植性较差。
2.1.2 动态反馈调节
动态反馈调节是指根据反馈信息对机械手的实际运动状态与模型的预期运动状态进行比较,并计算传感器测量值与模型计算值的误差,通过改变模型输出来实时调整机械手的运动,以缩小机械手的作业误差,使其能够按要求完成作业。
Tiano等[20]构建了水下自主航行器上配置的机械手的多变量动力学模型,为了最小化航行器与机械手的动态相互作用以及水环境的影响,根据机械手的运动反馈信息确定了动力学参数,并将得到的动力学模型用于航行器控制系统的设计。Balas等[21]对水下机械手在超低速和超高速下运动时的动力学模型进行了研究,基于运动状态反馈信息消除了超低速情况下的时间延迟和超高速情况下的非线性干扰。张钰等[22]以七功能水下电动机械手为研究对象,提出了一种通过力传感器感知机械手末端位置控制输出误差并在线调整的轨迹规划算法,以减小机械手末端的位置偏差,有效提高了机械手的作业精度。
动态反馈调节是基于传感器的反馈值来调节机械手的运动的,对采样频率及采样精度的要求较高[23-24],且由于水下环境不断变化,使得传感器的反馈值不稳定,从而导致水下机械手一直处于跟随状态,这会给机械手各关节的电机带来额外负荷,使得其在水下精准控制中的可靠性低,从而导致机械手运动不稳定。
2.1.3 控制策略优化
控制策略优化是指采用模糊理论或神经网络对水下机械手的控制系统进行改进,对机械手运动过程中因水环境影响而产生的不确定性参数进行估计和调整,以提高控制系统的抗干扰能力,从而降低水环境的影响。
陈显亭等[25]以六自由度SIWR-II 型水下机械手为原型,提出采用模糊小脑模型关节控制器(cerebel‐lar model articulation controller,CMAC)的控制理论对水下机械手进行动力学分析,并基于连续可微的高斯隶属函数在线调整模糊CMAC 的参数,同时根据该机械手的实际结构及参数对所提出的模糊方法进行仿真验证,结果表明该方法具有较高的抗干扰能力。杨超等[26]对水下机械手作业时引发的机器人动力学不稳定问题进行了研究,采用径向基函数(radial basis function,RBF)神经网络对机械手动力学模型的不确定性和水环境干扰进行了在线逼近,并结合自适应终端滑模控制器对水下机器人的控制参数和神经网络权值进行在线调节。Chatchanayuenyong等[27]采用基于神经网络的智能方法对水下机械手的动力学非线性参数进行了辨识,基于神经网络系统的输入与输出之间的关系,提出了一种基于神经网络的鲁棒非线性时间最优控制器,并通过试验验证了其可有效解决参数的非线性和不确定性问题。
基于模糊理论或神经网络设计的非线性控制器能有效提高水下机械手控制系统的精度与稳定性,使其在复杂多变的水下环境中具有较强的自适应能力[28-29]。但无论是模糊控制还是神经网络控制,都要进行大量的运算,这增大了水下机械手控制系统的复杂程度,使其难以应用于实时环境中。
2.2 基于水动力学模型的动力学建模方法
水下机械手在复杂多变的环境中工作,其稳定性决定了其作业能力。针对基于误差补偿的水下机械手动力学建模方法存在的不足[30-31],提出了基于水动力学模型的水下机械手动力学建模方法,即采用切片理论或条带理论对水下机械手进行受力分析[32],结合流域状态,通过数值模拟或实验分析来计算水动力学参数,并将计算得到的水动力学模型与机械手动力学模型结合,作为水下机械手控制系统的前馈项,以提高控制系统的通用性、稳定性与实时性[33]。
通过对水环境影响进行分析,直接构建水动力学模型,并将其引入水下机械手的动力学模型,可得:
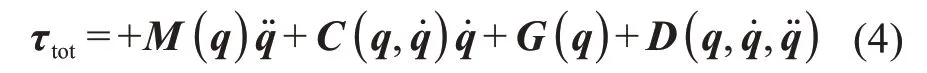
基于前馈思想,分析水下机械手的运动状态和水环境的影响,预测机械手在运动过程中所受的力矩,以降低水对机械手运动的干扰[34]。
Mclain等[35]基于单自由度旋转机械手,利用理论分析和实验方法对水动力项进行了计算并确定了水动力系数,还对其受到的阻力和附加质量力进行了分析,并利用水下机器人进行了验证实验,建立了其配备的水下机械手的动力学模型,并将基于动力学模型的前馈信息整合到机械手的控制系统中,以提高其作业能力。王华等[36]采用切片理论分析了水下机械手的动力学特性,并考虑了水环境的影响(包括水流对机械手的作用和机械手在水中运动时对自身造成的影响),同时通过仿真分析验证了水下机械手的动力学特性。Kolodziejczyk等[37]通过建立单自由度机械手模型,并基于条带理论分析了机械手在水下运动时受到的附加质量力和水阻力,然后采用CFD(compu‐tational fluid dynamics,计算流体动力学)仿真软件对水下机械手作不同运动时的受力状况进行了分析,确定了水动力系数,这可为水下机械手的动力学控制奠定一定的基础。Zhang 等[38]针对黏性水动力系数测定难度大的问题,建立了单自由度水下机械手模型,基于数值模拟方法对该机械手作业时受到的水环境的黏性影响进行了分析,并提出了一种瞬态黏性水动力系数的数值模拟方法,进一步完善了水动力学模型。
综上,现有文献对基于水动力学模型的水下机械手动力学建模方法的研究尚未深入[39],仍缺乏经大量试验验证且被广泛认可的方法,即尚未形成固定的研究方法。但是,对于水动力学模型的构建,目前已有大量较为完善的方法,下文将对惯性和黏性水动力学模型的构建方法进行总结。
3 不同水动力学模型的构建方法
水动力学模型的构建是水下机械手动力学分析的基础,其准确性会直接影响到机械手动力学模型的准确性,进而影响到控制模型的精确性。准确的水动力学模型可有效分析与预测水流的运动规律,进而准确分析水下机械手的受力情况。
水动力系数为时变参数且数量多,各系数之间还存在耦合,因此难以建立可准确表征水下机械手工作状态的水动力学模型,通常考虑为由加速度引起的惯性水动力及由摩擦引起的黏性水动力。
3.1 惯性水动力计算方法
理论研究表明惯性水动力与加速度有关,其系数(即水阻力系数和附加质量力系数)的数量较少,一般是一些固定的比例常数。这些比例常数可通过经验法估算、面元法计算以及平面运动机构法测定等手段来获取。
3.1.1 经验法
经验法是指利用已有的半经验公式或数据库,根据已测试过的且外形结构相似的模型样本的惯性水动力系数,分析得到适用于新模型的水动力系数。该方法的优点是简单方便,缺点是对象单一,不适合用于外形复杂的机械结构。
Nahon 等[40]对自主水下航行器的非线性动力学模型进行了研究,通过将航行器简化为指定的几何形状并对其进行分解,基于经验法对各基本元素进行了惯性水动力学建模分析,并结合校正系数确定了总的惯性水动力和力矩。肖治琥等[41]以三自由度四功能深海电驱动水下机械手为研究对象,基于Morison公式分析了其大臂、小臂的惯性水动力,并采用叠加原理将水下机械手在静水环境下运动时所受的力与静止时所受的水流干扰力相结合,得到了总的惯性水动力。Azarsina 等[42]对轴对称鱼雷形船体的惯性水动力系数计算方法进行了分析,通过将惯性水动力系数的线性化经验公式嵌入到轴对称水下航行器的动力学模拟计算中,基于仿真分析得到了水阻力系数和附加质量力系数并与理论结果进行了对比,而后利用海试数据对仿真模型进行了校准。
经验法适用于计算已有试验数据库的水下机械手的惯性水动力,其能预测外形规则的水下机械手运动时所受的水阻力和附加质量力,可充分利用现有资源,结合经验公式对惯性水动力系数进行估算。经验法的计算速度快,使用方便且成本低,但其适用范围在很大程度上取决于现有的研究数据,此外其预测精度难以保证。
3.1.2 面元法
面元法是指对结构特征面进行离散和划分网格,用平面或曲面代替原特征面,基于面元求解惯性水动力的方法。计算惯性水动力时须进行计算空间和积分方程的双重离散,其中:计算空间的离散是指对结构表面进行网格划分,以得到四边形曲面或三角面;积分方程的离散是指用离散变量代替连续变量,将线性积分方程转换成线性代数方程组。
张玲等[43]以形状复杂的水下机器人为研究对象,采用CAD(computer aided design,计算机辅助设计)方法对水下机器人表面进行网格划分并获取面元坐标(如图3(a)所示),通过计算得到了其所受的惯性水动力,并拟合得到了水阻力系数和附加质量力系数。杨磊等[44]采用面元法编写了任意三维物体附加质量的计算程序,并利用Gambit软件对水下滑翔机模型表面进行网格划分(如图3(b)所示),获取了表面的节点信息,将其导入所编写的程序,通过计算得到水下滑翔机的附加质量,并与仿真结果进行对比,验证了面元法的可行性和准确性。庞永杰等[45]采用面元法分析了2个水下物体在相互接近过程中的惯性水动力,通过计算得到了惯性水动力系数随物体间距离的变化曲线,试验结果验证了面元法对相互接近的任何形状的物体均适用。

图3 基于面元法的网格划分Fig.3 Meshing based on panel method
面元法适用于计算具有回转特性的水下机械手的惯性水动力,其计算空间的离散大多采用CAD方法,操作简单;其积分方程的离散大多采用数值方法,效果理想。基于面元法计算得到的惯性水动力的准确度高于经验法,但其计算过程较复杂,导致其应用范围小于经验法。
3.1.3 平面运动机构法
平面运动机构法是指采用水平面及竖直面的特定运动(如图4所示)来模拟机械装置在水环境中的运动,然后系统地求取其运动时产生的力和力矩,进而得到其加速度导数与速度导数。

图4 平面运动机构法示意Fig.4 Schematic diagram of plane motion mechanism method
董苗苗等[46]基于平面运动机构法对2 种水平面和2种垂直面的非定常运动进行了数值模拟,运用叠加原理计算得到相应的惯性水动力和力矩,并运用傅里叶积分和数据拟合等方法对计算结果进行处理,获取了对应的惯性水动力系数。杨磊等[47]采用平面运动机构法对水下滑翔机进行了仿真试验,得到了给定运动下的惯性水动力和力矩,并通过分析处理求取了对应的惯性水动力系数,通过与基于面元法得到的结果进行对比,验证了该方法满足工程需求。范士波等[48]建立了4 500 m级深海作业型ROV的缩尺比模型,采用平面运动机构法对其进行水动力试验,包括各方向的阻力试验和操纵性试验,通过计算得到了对应的惯性水动力系数,并将其应用于运动控制器的设计。
平面运动机构法适用于计算非定常运动下水下机械手的惯性水动力,通过对运动性质的分析和运动叠加来计算对应平面运动的惯性水动力和力矩。该方法可通过预设水下机械手的运动轨迹来求解对应的运动阻力,进而计算惯性水动力,其求解方式较为系统化且理论性强,但在精确性要求高的应用场合中,须进一步结合面元法或其他方法进行对比分析。
3.2 黏性水动力计算方法
理论研究表明黏性水动力的计算要比惯性水动力困难,且其系数的数量众多。目前,较为可靠的黏性水动力计算方法有模型试验法、系统辨识法和CFD 数值模拟法,已有众多研究证明了这些方法的有效性。
3.2.1 模型试验法
模型试验法包括实体试验法和比例试验法。实体试验是指将机械装置实体模型放置在实际环境中进行任务测试;比例试验是指将通过放大或缩小实体模型得到的试验模型放置在模拟的作业环境进行任务测试。
Lin等[49]以单连杆水下机械手为研究对象,分别在水平角运动模式、垂直角运动模式以及线性运动模式下进行水池试验,量化得到了该机械手的黏性水动力系数。钟朝廷等[50]将英国SMD 公司生产的ROV按1∶4的比例缩小为几何外形和作业特点相同的试验模型(如图5所示),通过拘束模型试验得到了其黏性水动力和力矩,并利用最小二乘法拟合得到了对应的无因次水动力系数。Filaretov 等[51]考虑到在水环境影响下水下机械手运动时会产生很大的力和扭矩,提出了一种基于动量传递的黏性水动力系数计算方法,并基于图6所示的空气动力学试验装置开展了空气动力学试验以确定黏性水动力系数,最后通过在实际海洋环境中的实体试验验证了该方法的准确性。

图5 ROV的试验模型Fig.5 Test model of ROV

图6 空气动力学试验装置Fig.6 Aerodynamics experimental device
模型试验法适用于计算对流体特性及外界干扰要求不高的水下机械手的黏性水动力,可通过专门的设备进行试验测试以准确地分析水动力的影响。在模型完备的条件下,该方法操作便捷且获取水动力的速度较快及结果准确,但耗时费力且具有尺度效应,同时也无法分离由不确定因素造成的影响,此外还不便于通过修改水体参数和机械装置几何形状来进行水动力学模型的优化。
3.2.2 系统辨识法
由于动力学模型具有非线性、强耦合的特性以及水下工作环境复杂,在建立了水下机械手动力学模型后,须对模型中的未知参数进行辨识,以更有效地控制水下机械手。
Fang等[52]对六自由度带缆遥控水下机器人的运动特征进行了分析,建立了相应的水动力学模型,通过仿真试验获得了特定运动下的黏性水动力系数,并结合极大似然法及遗传算法完成了水动力系数的辨识。刘建成等[53]对水下机器人的水平面运动进行了探讨,建立了包含水动力系数的数学模型,采用极大似然参数估计法辨识得到该水下机器人的黏性水动力系数,并基于辨识得到的水动力系数建立了水下机器人的运动模型。袁伟杰等[54]提出了一种基于遗传算法的水动力系数辨识方法,该方法不受参数初始值的影响,仿真结果表明该方法能有效辨识水下机器人的黏性水动力系数,其具有较好的鲁棒性和全局寻优特性。
系统辨识法适用于计算已建立动力学模型且存在待求解系数的水下机械手的黏性水动力。当机械手按预设轨迹运动时,建立运动轨迹信息数据库,并采用遗传算法或极大似然法等优化方法对水动力学模型中的未知参数进行求解。该方法具有良好的辨识效果且不受参数初始值的影响,可为运动控制和状态预测等提供更为准确的数据。
3.2.3 CFD数值模拟法
CFD数值模拟法是指运用Fluent等软件,在设定的特定条件下分析流场中机械装置模型的受力,进而计算黏性水动力系数。
Irwin等[55]比较了各种湍流模型和网格划分方法对黏性水动力系数的影响,通过与工程试验方法对比,验证了基于CFD 数值模拟法得到的结果是准确的。Racine 等[56]基于非线性模型、非定常雷诺-时均方程和斯托克斯方程,采用CFD 数值模拟法分析得到水下航行器的黏性水动力系数,并与理论计算结果进行了比较,验证了该方法的可行性。王太友等[57]基于CFD 数值模拟法对复杂ROV 的水动力性能进行了仿真分析,并将数值仿真结果与试验结果进行对比,验证了该方法的可行性和准确性。胡志强等[58]提出了一种水下机器人黏性水动力的数值计算方法,并通过CFD仿真软件对自治水下机器人的黏性水动力进行了计算,结果表明基于该方法获得的黏性水动力系数具有较高精度。
CFD数值模拟法适用于计算复杂水流环境下复杂外形的水下机械手的黏性水动力,其采用的数值支撑技术(网格生成、并行计算和可视化等)能够很准确地模拟黏性流场以及精确预测机械手周围复杂的湍流流场,可提供许多难以通过试验得到的水动力信息。CFD数值模拟法的计算周期短且不存在尺度效应,可预测惯性、黏性水动力,优势明显。诸多研究证明了CFD 数值模拟法的准确性,其目前已是黏性水动力的主流计算方法。
4 结论
本文对水下机械手的功能和设计特征进行了总结,针对不同海上应用区域,水下机械手的功能多样。对水下机械手动力学模型的构建方法进行了详细介绍,并对2种消除水环境影响的方法进行了具体分类和详细比较,主要结论如下。
基于误差补偿的水下机械手动力学建模方法是通过改进控制方案来补偿机械手实际运动与期望运动之间的误差,即根据误差进行实时调整,使得机械手能够按预设的轨迹运动,完成作业;基于水动力学模型的水下机械手动力学建模方法是从前馈信息出发,根据机械手的运动趋势与水环境对机械手产生的干扰力进行建模分析,进而实现对机械手的高效控制。基于水动力学模型的水下机械手动力学建模方法已逐渐被国内外机器人领域专家认可,其应用前景非常广阔。
由于实际水环境复杂多变,目前基于水动力学模型的水下机械手动力学建模方法仍停留在理论仿真阶段,只开展过少量的浅水实体试验,说明其应用于实际海洋或复杂水流环境的难度较大,这将是未来须重点研究的内容。

