非均匀Kuramoto振子系统的频率同步

熊河浪，张 华

(重庆理工大学 理学院， 重庆 400054)

群体运动一直是近几十年国内外众多学者研究的重要问题，其中耦合振子系统是研究热点问题之一。17世纪物理学家惠更斯发现了两邻近钟摆同步的振动现象。随后，Kuramoto Y[1]提出的耦合振子模型解决了钟摆的同步特性问题，并可以描述自然界中很多集群同步现象。振子集群同步现象在物理、生物、化学、社会等不同领域具有非常广泛的应用，如在物理和化学中，用于自旋玻璃模型的建模和分析[2]、Josephson结阵列的同步现象[3]、原子反冲激光中的同步现象[4]、中微子的味道演化[5]、电化学振荡器中的同步现象[6]、在互联网连接网络中各路由器同步发射信号时发生的网络堵塞现象[7]；在生物中，心脏起搏器细胞[8]、昼夜节律[9]、神经科学[10]、动物群集行为[11]、鱼群涌现[12]等。

早期Kuramoto振子模型常是基于平均场耦合的，其解析处理方法一般基于平均场理论和自洽方法，如Thomas等[13]通过大型网络上的广泛数值模拟，系统地比较了非均匀度平均场(HMF)和淬灭平均场(QMF)方法的预测结果。Yook等[14]研究了Kuramoto振子在去同步阶段的2个不同阶参数的行为。Wesley等[15]分析了2个改变标准的易感-感染-易感(SIS)动力学模型。随后有学者开始将Kuramoto振子模型转化为梯度系统的形式，利用Lojasiewicz不等式理论分析该振子模型(梯度系统形式)的动力学行为[16]。

1阶Kuramoto振子的模型还拓展到不同的连通拓扑效应、噪声效应、混杂耦合形式的效应以及复杂网络连接效应等多种复杂外部和内部环境中考虑[17]。2阶Kuramoto振子的模型可以拓展到固有频率服从不同的分布、相位延迟等制约因素下考虑。常用于分析模拟动物群集行为的粒子模型[18]、结构保持的电力系统模型[19]、网络简化电力系统模型[20]、耦合节拍器[21]等。如Choi等[22]利用Gronwall不等式方法分析有限惯量Kuramoto振子的渐近完全相频同步，Koditschek等[23]利用Lyapunov稳定性理论证明了闭环机械控制系统的几乎全局渐近稳定性，Dörfler等[24]利用奇异摄动理论分析了摇摆方程与非均匀Kuramoto模型之间的关系等。然而，这些方法或者完全局限于2阶Kuramoto振子，或者只适用于均匀惯性和单位阻尼，或者需要充分小的惯性系数。因此，本文给出了一个充分条件改进现有方法，使结果应用更加普遍。

本文提出了一个使2阶Kuramoto振子达到频率同步的充分条件；重新定义了振子的频率同步和相位内聚，将本文结果和奇异摄动方法得到的结果进行对比，发现在满足一定的条件下惯性项对于同步的发生无影响，通过计算机数值模拟进一步验证了充分条件的正确性。

1 预备知识

给定Rn空间中，元素全为1的向量记为1n，向量z∈Rn的2范数和∞范数分别记为‖z‖2和‖z‖∞；In表示n阶单位矩阵[26]。

给定一个无向连通图G=(V，E，A)，V= {1，2，…，n}表示所有顶点的集合，记e为总边数， {1，2，…，e}=E⊂V×V表示顶点之间构成边的集合，A=[aij]∈Rn×n表示图G的邻接矩阵，其中权重aij>0，且A=AΤ[26]。

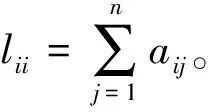
如果diag({as}s∈{1，2，…，e})是边权重的对角矩阵，那么对应的拉普拉斯矩阵为L=Bdiag({as}s∈{1，2，…，e})BΤ[26]。

Brouwer’s不动点定理：假设X⊂Rn是一个非空紧凸集，f∶X→X为连续映射，则存在x*∈X，使得f(x*)=x*[27]。

2 问题阐述

考虑连通图G中具有n≥2个的2阶Kuramoto振子系统：

(1)

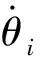
记θ=[θ1，θ2，…，θn]Τ∈Rn，令Φ(θ)=BΤθ表示角的增量。同理，ω=[ω1，ω2，…，ωn]Τ∈Rn，Φ(ω)=BΤω表示固有频率的增量。

定义1给定常数α∈[0，π/2)和上述θ，若||Φ(θ)||∞≤α成立，则称系统(1)是相位内聚的。

定义2对于任意充分小的正数ε，如果||Φ(ω)||∞≤ε成立，则称系统(1)是频率锁相的或者是频率同步的。

带有惯性项的2阶Kuramoto振子可以写成如下梯度系统：

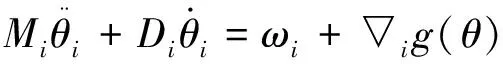
(2)

3 主要结果

引理1[26]无向连通图G的拉普拉斯矩阵L是可对角化的，即L=Udiag(0，λ2，…，λn)UΤ，U∈Rn×n表示正交矩阵，令L†∈Rn×n是L的加号广义逆，记：

L†=Udiag(0，1/λ2，…，1/λn)UΤ

(3)

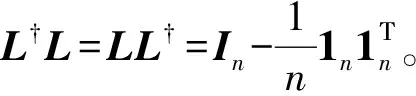
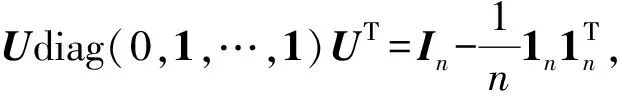
证明：首先对式(1)的所有方程求和，得：

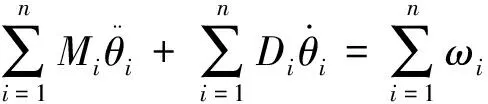
(4)

定义如下1阶Kuramoto振子系统：

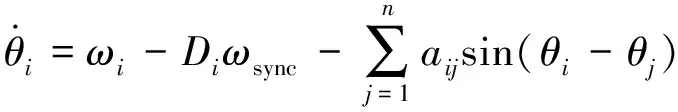
(5)

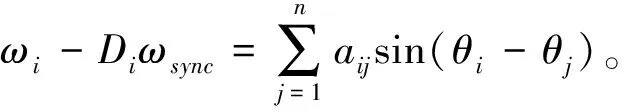
定义：

由于Φ(θ)=BΤθ，那么平衡方程可转化为：

ω-Dωsync=Bdiag({as}s∈{1，2，…，e})sin(BTθ)=

Bdiag({as}s∈{1，2，…，e})y(BTθ)BTθ=

(6)

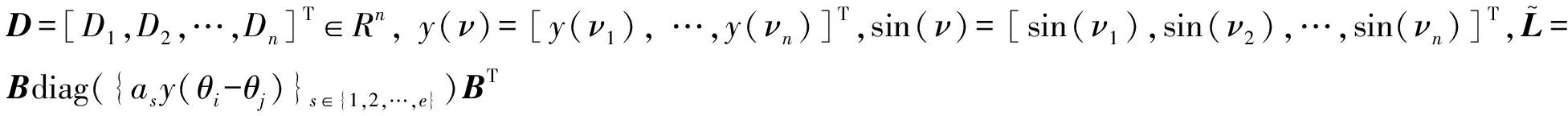
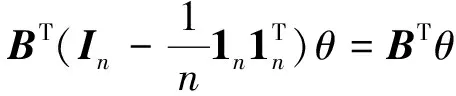
(7)

式(7)左边是θ∈Ω的连续函数。若存在紧凸集Γ∞(α)={x∈Rn∶‖x‖∞≤α}，使x=BTθ∈Γ∞(α)，则式(5)存在一个平衡θ∈Ω。

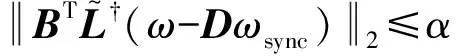
||BTU(x)diag(0，γ2，…，γn)UT(x)(ω-Dωsync)||2≤

γ2||BTU(x)diag(0，1，…，1)UT(x)(ω-Dωsync)||2=

γ2||BT(ω-Dωsync)||2

(8)

对于x∈Γ2(α)，有：

(9)

当ν∈(0，π/2)时，y(ν)=sin(v)/v的值域为(0，1]，故λ2(L)≥λ2(L)y(ν)，因此1/λ2(L)≤ 1/(λ2(L)y(ν))。

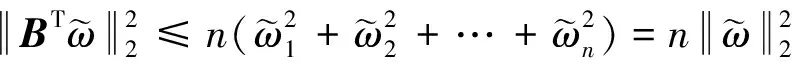
又||x*||2≤α，则式(9)等价于：

(10)

即：

λ2(L)sin(α)≤λ2(L)

(11)

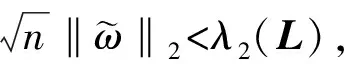
注1 在定理1条件下，当α∈[0，π/2)时，相位差满足‖θi-θj‖∞<α；对于任意充分小的ε，固有频率满足‖ωi-ωj‖∞<ε，则式(1)处于同步平衡状态。

奇异摄动分析[28]假设式(1)是过阻尼的，即Di>>Mi。定义扰动参数ε=Mmax/Dmin，其中：

Mmax=max{M1，M2，…，Mn}

Dmin=min{D1，D2，…，Dn}

或

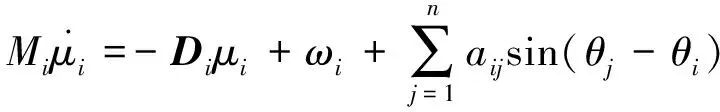
在等式两边同时乘以ε，得：

(12)

在式(12)两边同时除以Mi，得：

(13)

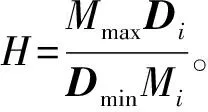
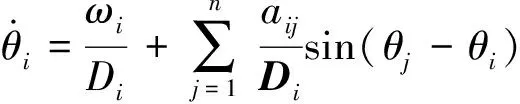
(14)

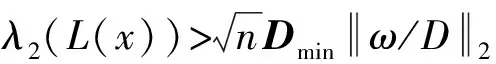
4 数值模拟

考虑n=5的情形，设固有频率初值ω=[0.01，0.02，0.03，0.04，0.05]T，阻尼系数初值D=[3，1，4，2，3]T，相位初值θ= [π/4，π/3，π/6,π/5,π/6]T，邻接矩阵为：

系统(5)在时间[0，5]内，利用奇异摄动分析得到振子的演化曲线，如图1所示。

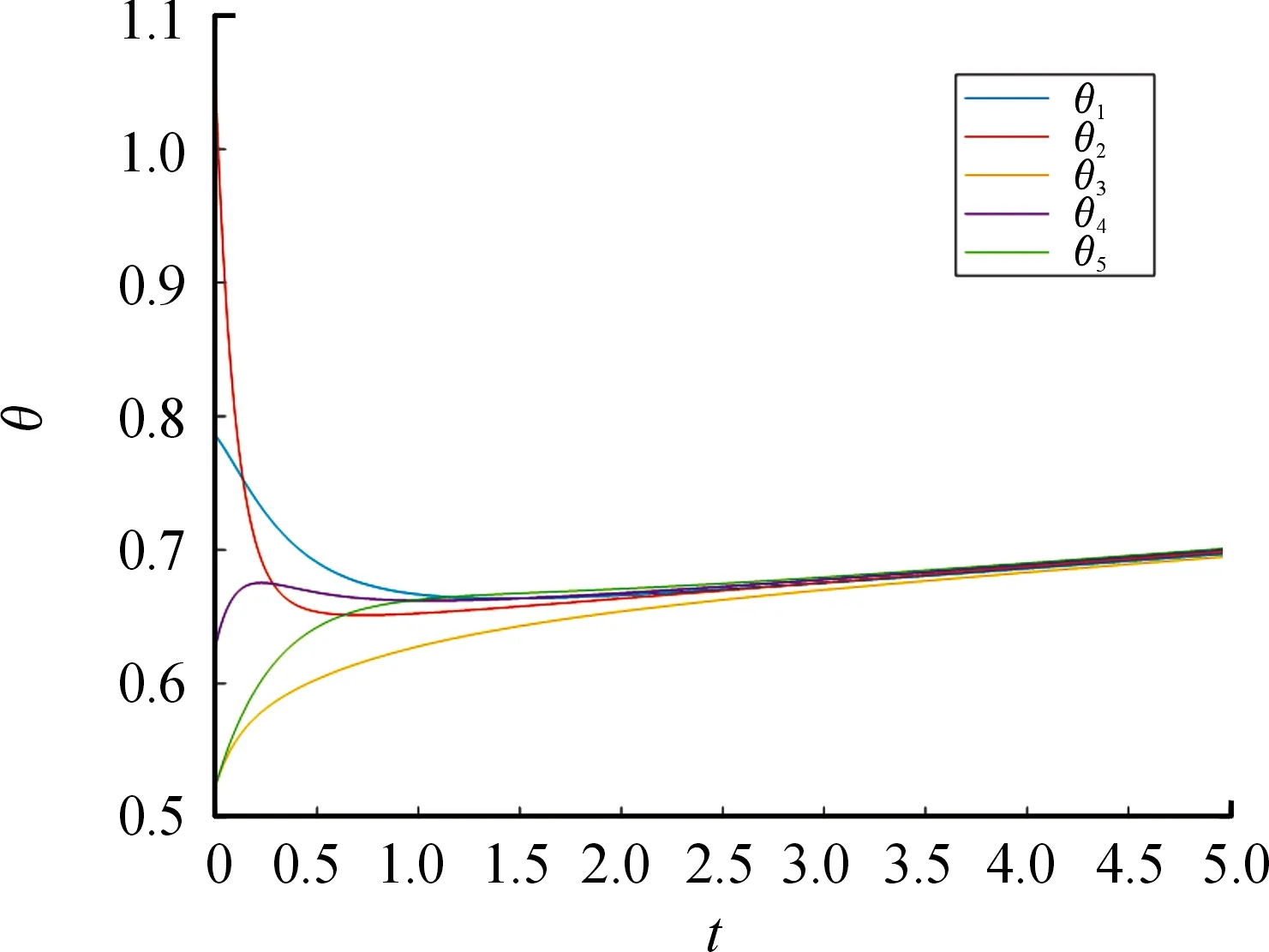
图1 满足条件Di>>Mi，时，振子同步曲线

系统(5)在时间[0，5]内，模拟满足定理1条件，得到振子的演化曲线，如图2所示。

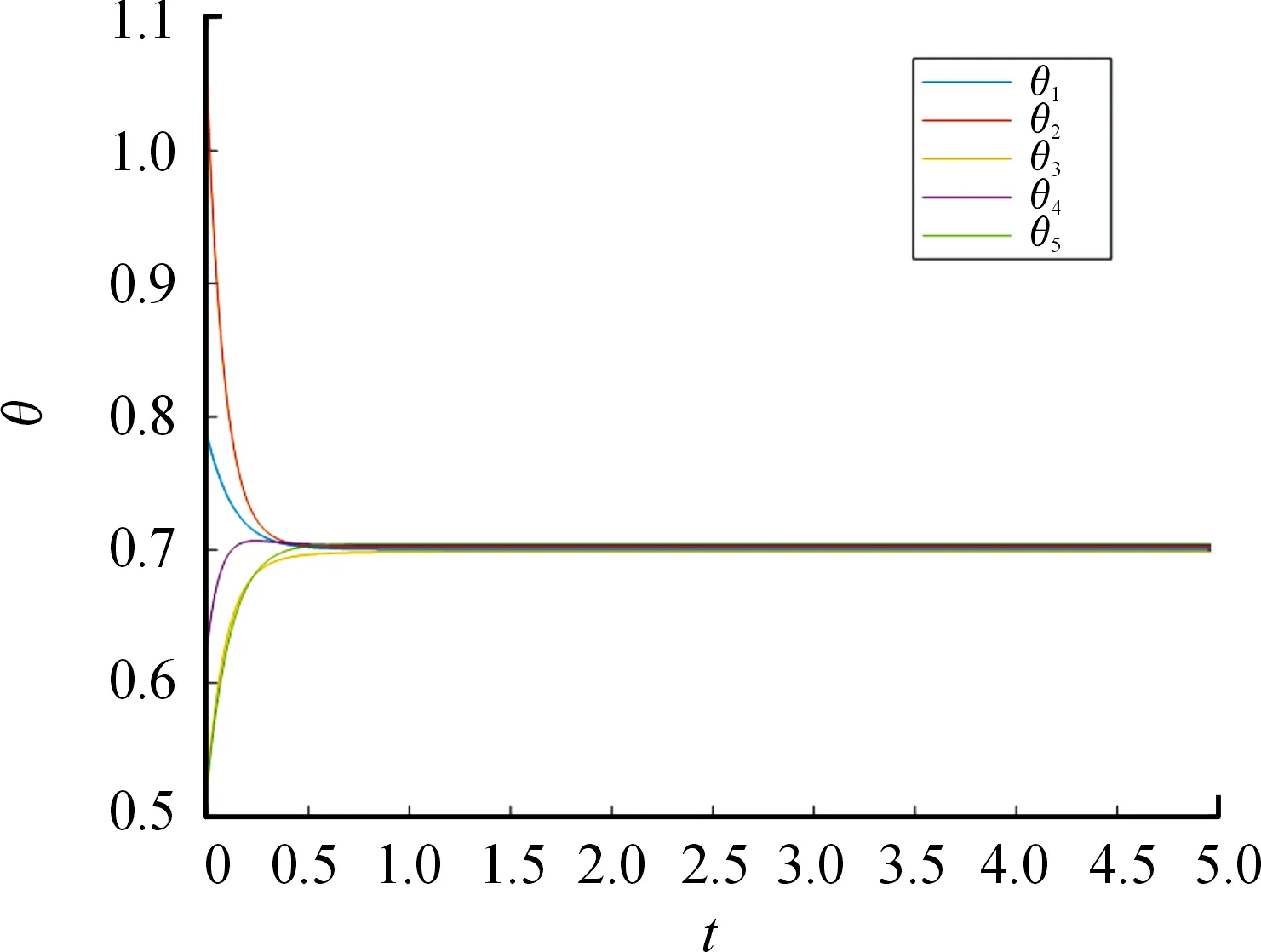
图2 满足条件时，振子同步曲线

系统(5)在区间[0，5]内，模拟不满足定理1条件，得到振子的演化曲线，如图3所示。

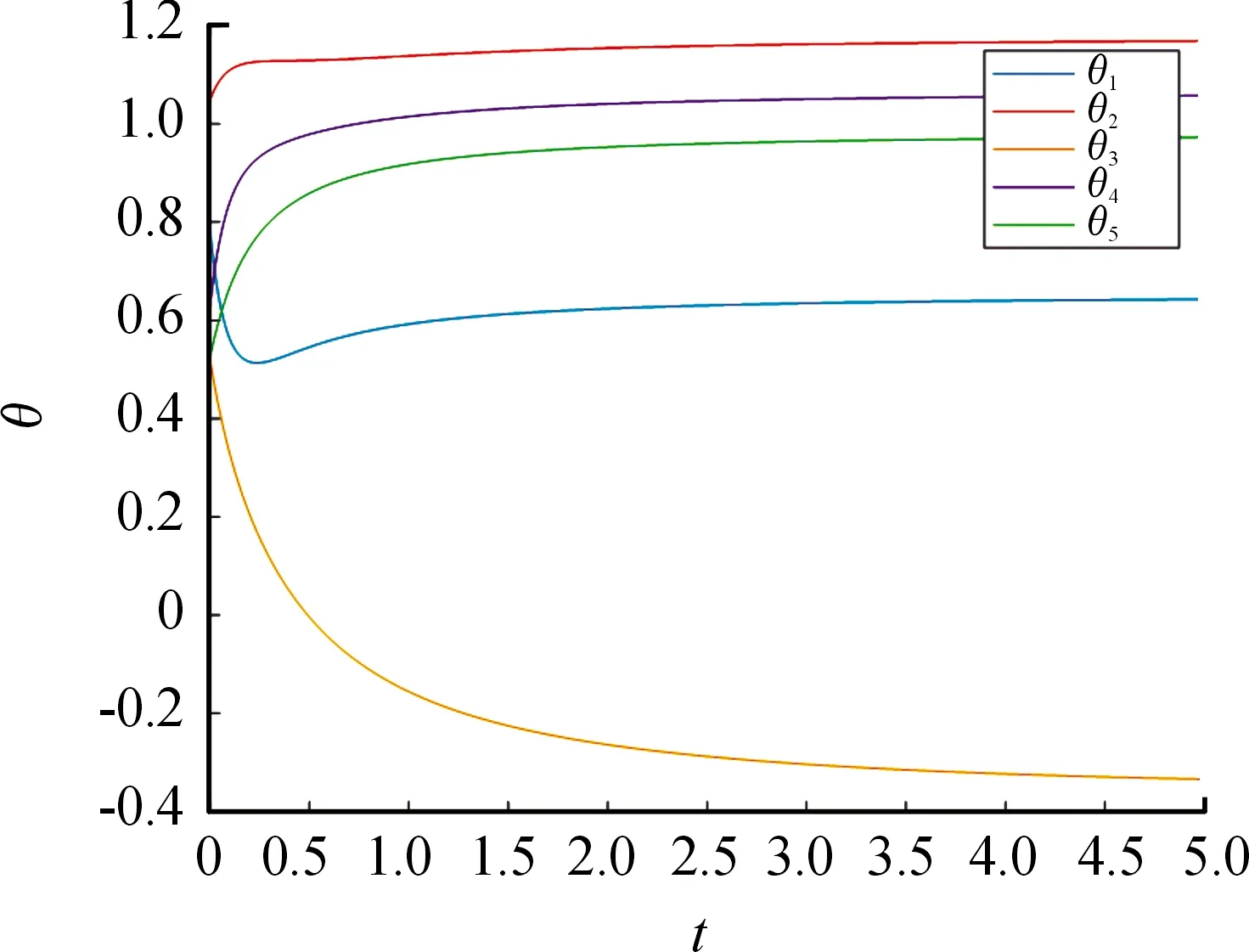
图3 不满足条件时，振子不同步曲线

注2定理1的方法是通过构造紧凸集，运用不动点定理，得到惯性项，不会影响同步发生。奇异摄动理论是使阻尼系数远大于惯性系数，通过计算找到一个充分条件，得出惯性项，会影响同步发生。因为惯性系数对于同步发生一直是有争议的，在其他文章中也提到这个问题[29]。所以，通过2种情形的对比，在满足一定的条件下，争议是可以避免的。参考图1、2，系统(5)最终会都会收敛到相同的数值。

下面验证当振子数目n=2时，得出的结论是否与定理1给出的充分条件一致。模型如下：

(15)

(16)

其拉普拉斯矩阵为：

对应的特征值为λ1=0和λ2=2a。给出一个差分函数h∶R→R：

(17)

图4 不同K值下的零点分布图

5 结论

主要讨论了2阶Kuramoto振子的频率同步问题，在满足充分条件的情况下，所有振子之间的相位差都趋于零，即系统(1)达到同步。

提供的方法适用于1阶和2阶Kuramoto振子等价的情形，而在不等价的情形是否可以运用这个方法还需进一步研究。本文可以推广到其他情形，如将固有频率推广到时变的固有频率、在振子间的相互作用函数中加入相位延迟、惯性系数与阻尼系数的其他比率等。上述情形都是需要继续研究的方向。