基于信赖域改进的动态Kriging模型的冲压成形工艺参数优化
冯美强,谢延敏,王东涛,郭元恒
(西南交通大学 机械工程学院, 成都 610031)
有限元仿真技术在冲压成形工艺开发上的应用能有效地减少开发时间与成本。然而板料成形是一个非线性过程,仿真计算复杂,仍然十分耗时。于是,通过反复调用仿真模型进行试验的方法优化板料成形工艺,但仍十分繁琐。将代理模型优化方法应用到板料成形工艺开发上可以提高效率,缩短开发周期。常用的代理模型有径向基函数(RBF)、人工神经网络(ANN)、Kriging、支持向量回归机(SVR)等[1]。Kriging代理模型是方差估计最小的无偏估计随机过程,具有提供预测响应和预测方差的能力,在工程优化领域受到了广泛关注。Feng等[2]基于Kriging模型对板料成形过程变压边力进行优化,提高了零件的成形质量。Hamdaoui等[3]基于Kriging模型对CPU密集型钣金成形进行多目标优化,减小了成形件的回弹,并消除了起皱与拉裂现象。岳跃鹏等[4]使用Kriging与水平集方法对压边圈结构进行优化,提高了十字杯型件成形的均匀性。
使用合适的加点策略对Kriging模型完成更新,可以提高代理模型的预测精度与算法的效率[5]。Jonse等[6]提出了期望最大加点准则(EI),该准则同时考虑代理模型的预测值与预测方差,很好地平衡了算法的全局搜索与局部探索。Zhong等[7]将EI加点准则与最小响应面加点准则相结合,发展了一种并行加点策略。谢延敏等[8]基于EI加点准则提出一种并行加点准则,提高了建模精度与算法收敛速度,并对翼子板成形工艺进行了优化。王超等[9]使用最小响应面加点准则(MSP)对EI加点准则进行改进,提高了算法后期的收敛精度与速度。对优化空间进行动态缩放,可以提高代理模型在优化空间内的建模精度与优化效率。Li等[10]应用模糊聚类对设计空间进行缩减与合并,提出基于模糊聚类的代理模型全局优化策略。Alexandrov等[11]将信赖域的思想引入到代理模型的管理与更新过程中,提高了代理模型的近似精度。龙腾等[12]提出基于信赖域的动态径向基函数优化策略(TR-DRBF),并将该方法应用到“工”字梁的优化中。曾锋等[13]将信赖域的思想与Kriging结合,提出了集成信赖域与最小置信下限的优化策略(IMTR-LCB)。
改进的混合加点准则充分利用了EI加点准则的全局搜索能力与信赖域方法能提高Kriging建模效率的能力,并通过最小响应面加点准则提高算法的收敛精度。将NUMISHEET2002标准考题中翼子板作为研究对象,以5条拉延筋的阻力作为设计变量,并且将板料成形困难区域[14-15]的减薄率作为响应值,进而基于改进的混合加点准则构建动态Kriging模型,利用粒子群算法进行优化。结果表明:该方法能有效消除板料的拉裂缺陷,提高成形质量。
1 Kriging代理模型
Kriging模型是基于统计理论的方差最小无偏估计模型,响应值与自变量之间的关系表示为:
y(x)=fT(x)β+Z(x)
(1)


(2)
MSE=E(c(x)TY-y(x))2
(3)
式中:c(x)为待求响应值权重系数向量。
2 基于信赖域改进的动态Kriging优化策略
2.1 期望最大加点准则(EI)

(4)
式中:Φ(·)为标准正态累积分布函数;φ(·)为标准正态概率密度函数。
2.2 改进的混合加点准则
2.2.1混合加点准则
混合加点准则针对EI加点准则中EI函数失效的问题,利用最小响应面加点(MSP)对EI加点准则进行改进。具体方法为:基于EI函数设定一个阈值CEI,当EI函数值大于CEI时,混合加点使用EI函数获取新样本点,当EI函数值小于CEI时,利用序列二次规划法(SQP)搜索当前EI点附近的局部最小值点完成加点。混合加点准则的适应度函数如下:

(5)
式中:CEI=0.001ymin,ymin为当前模型最小响应值。
2.2.2基于信赖域方法的期望最大加点准则
使用信赖域方法对优化空间进行缩放能提高算法的优化效率,基于信赖域的全局优化算法的具体步骤如下:
1) 确定设计样本空间B,使用拉丁超立方抽样抽取10m组样本,m表示设计空间的维数,建立初始Kriging模型。

(6)
式中:l0为初始设计空间长度;n为迭代次数;r为优化空间缩放参数。
2.2.3基于信赖域改进的动态Kriging优化策略
基于信赖域的EI加点准则由于空间的缩放,引起EI函数值过小,进而导致加点准则失效。将信赖域方法与混合加点准则进行集成,提出一种改进的混合加点准则,能有效地解决这一问题,提高算法寻优的速度与收敛精度。
将改进的混合加点准则与Kriging优化方法结合,提出了一种基于信赖域改进的动态Kriging模型优化算法,具体步骤如下:
1) 确定设计样本空间B,使用拉丁超立方抽取样本10m组,m表示设计空间的维数,建立初始Kriging模型,并记迭代步数k=1。
2) 当k=1时,优化空间为初始设计空间,当k>1时,则使用信赖域方法对优化空间进行更新。
第一,在国有企业内部建立良好的控制环境。良好的内部控制环境,对实现国有企业的对内控制有着重要的促进作用,这就需要企业从自身经营发展的实际情况出发,制定明确具体的企业改革执行策略,并对内部控制管理制定加以完善,为进行企业内部管控营造良好的氛围,确保国有企业领导人可以严格按照行之有效的规章制度做好相关的企业管理控制工作。同时企业中的各个层级和部门还应加强交流程度,实现对任务的合理分配,从而实现企业内部的有效管理。
3) 使用粒子群求解混合加点准则获取新的样本点,并求其响应值,然后更新Kriging代理模型。
4) 判断当前最优值是否满足收敛条件,如果满足,则结束;不满足,则跳转至步骤2)继续迭代。
基于信赖域改进的动态Kriging模型的优化算法基本流程如图1所示。

图1 基于信赖域改进的动态Kriging模型优化算法基本流程框图
2.3 测试算例
为了验证基于信赖域改进的动态Kriging优化策略的有效性,选择GP函数、HD6函数分别对改进的混合加点优化策略、经典的EGO优化算法、基于信赖域的动态径向基代理模型优化策略(TR-DRBF)和集成信最小置信下限和信赖域的动态代理模型优化策略(IMLCB-TR)等优化策略进行测试。
1) Goldstein-Price(GP)函数
f(x)=[1+(x1+x2+1)2(19-14x1+
[30+(2x1-3x2)2(18-32x1+
(7)
该函数在定义域内取4个局部最小值,在(0,1)处取得全局最小fmin=0。
2) Hartmann 6-Dimensional Function(HD6)函数
(8)
式中:xi∈[0,1],i=1,2,3,4,5,6;α=(1.0,1.2,3.0,3.2)T;Aij,Pij的表达式如下:

函数i=6,在x=(0.201 7,0.150,0.477,0.275,0.311 8,0.657 3)处取得最小值fmin=-2.223 7。利用4种优化策略分别对测试函数各优化10次,并统计其优化结果,如表1所示。

表1 测试函数优化结果
从表1中可以看出,基于信赖域改进的动态Kriging优化算法在非线性函数的优化中能较快地收敛到函数的最优值,与其他3个优化方法相比,该方法能保证收敛精度,且优化耗时较少。
3 基于信赖域改进的动态Kring的翼子板成形优化
3.1 翼子板成形拉延筋模型
以NUMISHEET2002标准考题中翼子板为研究对象,基于冲压仿真软件DYNAFORM建立有限元仿真模型,如图2所示。其中,板料的材料参数以及成形工艺参数如表2所示。

图2 翼子板仿真模型示意图

表2 材料参数与翼子板成形工艺参数
翼子板成形较为复杂,在成形过程中需要保证材料在各个方向上充分流动。仅对压边力、摩擦系数等工艺参数进行简单调整并不能消除板料成形缺陷。通过在模具上布置拉延筋可以精准地控制材料在各个方向的流动,提高板料成形质量。参照NUMISHEET2002在翼子板冲压模具上布置了5条拉延筋,如图3所示。拉延筋阻力的取值范围如表3所示。

图3 5条拉延筋布置与y=100截面选取示意图
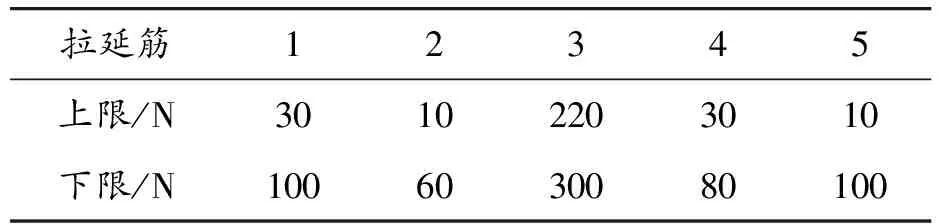
表3 拉延筋阻力取值范围
为了验证有限元模型的有效性,保证优化结果真实可靠,使用DYNAFORM对有限元模型进行仿真计算,并按图3所示的y=100截面,测量截面的主应变,结果如图4所示。从图4中可以看出,本模型仿真结果与标准考题基本一致,因此有限元模型的可靠性得到了验证。
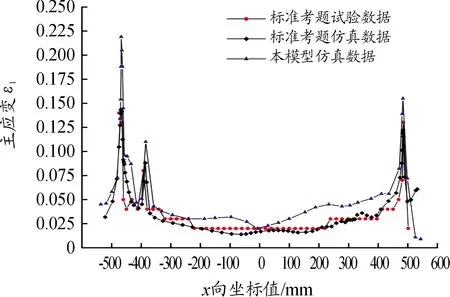
图4 y=100截面主应变曲线
3.2 基于改进的动态Kriging模型的工艺参数优化
3.2.1优化目标
翼子板在成形过程中的主要缺陷为拉裂缺陷,为了消除拉裂缺陷,一般选取减薄率作为成形质量指标[16]。通过关注板料成形困难区域,建立工艺参数与成形困难区域减薄率之间的Kriging代理模型。优化目标如下:
(9)
式中:ε1为板料成形的主应变;ε0为成形困难区域筛选参数;n为所选区域的单元总数;δ0为板料的初始厚度;δi为第i个单元的厚度。
3.2.2翼子板成形工艺参数优化
基于拉丁超立方抽样方法,对所布置的5条拉延筋的阻力在取值范围内抽取50组样本,利用DYNAFORM建立有限元模型进行仿真,并计算其成形质量指标。抽取的部分样本如表4所示。
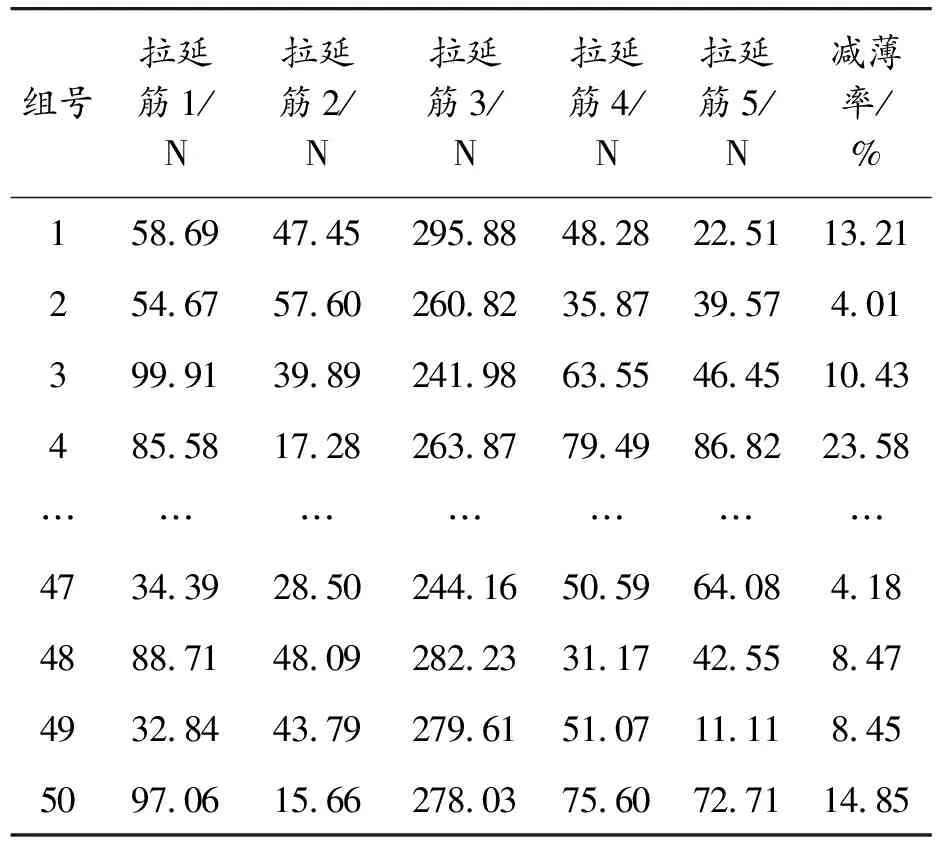
表4 初始建模50组样本
建立5条拉延筋阻力与目标减薄率之间的Kriging模型,使用粒子群算法对初始Kriging模型进行寻优,得到初始Kriging模型的5条拉延筋的最优阻力组合。将通过初始代理模型得到的最优拉延阻力代入有限元模型计算,结果如图5所示。这2个图由有限元仿真软件DYNAFORM自动生成。在成形极限图中,成形极限曲线、安全裕度曲线、单向拉伸和双向拉伸曲线等将图中区域分为安全区、起皱区和拉裂区等。图5(a)为PSO优化后的成形极限图,图5(b)为PSO优化后的成形云图。

图5 PSO优化后的成形极限图和成形云图
使用改进混合加点优化策略对Kriging模型进行动态更新,并通过粒子群算法对模型寻优。加点优化后得到最优拉延阻力,如表5所示。

表5 混合加点准则优化所得拉延筋最优阻力
将最优拉延筋阻力代入有限元模型进行计算,结果如图6所示。这2个图也是有限元仿真软件DYNAFORM自动生成。图6(a)为加点优化后的成形极限图,图6(b)为加点优化后的成形云图。

图6 改进的混合加点策略优化结果成形极限图和成形云图
将改进的混合加点准则用到翼子板成形工艺参数优化中,对Kriging模型进行动态更新,然后使用粒子群算法进行优化,得到翼子板成形的最佳工艺参数,消除了拉裂缺陷,提高了板料成形质量。
4 结论
1) 提出了改进混合加点准则。通过非线性函数测试,表明基于该加点准则的Kriging优化算法在非线性函数中能高效收敛到全局最优值。
2) 将成形困难区域的减薄率作为质量评价指标,降低了非成形区域与易成形区域对成形质量评价指标的影响,提高了优化效率。
3) 以翼子板为研究对象,基于改进的混合加点准则,使用Kriging代理模型优化方法获得了翼子板成形最优工艺参数组合,消除了拉裂缺陷,提高了成形质量。

