基于改进粒子群算法的EV充电站站址与检测工作规划*
陈年 李波 韩忠 / 泰州市计量测试院
0 引言
近年来,我国电动汽车(Electric Vehicle,简称EV)进入飞速发展新阶段,成交量连续5年位居全球第一,累计销售超过480万辆,占全球机动车销售总额的一半以上。而充电站的合理规划与建设是大规模推广EV的保障,目前我国已经投入使用的交、直流充电桩共计343 998个,到2020年全国范围新增集中式充换电站超过12万座,分散式充电站超过480万个。
但是,目前充电站却存在着布局不合理,使用率过低等问题,充电桩沦为“摆设”。同时,对EV充电桩的计量性能提供检测服务成为与人们生活息息相关而又急需解决的问题。因此,对充电站进行适度超前且合理的规划布局不仅能提高充电站的使用率,还能降低政府和检验检测机构、充电站设备投资建设者、EV用户的成本,最终促进整个EV产业链的发展。
目前,对于充电站站址规划国内外学者已展开了大量研究。文献[1]针对目前EV的使用现状,提出了充电站规划的因素和遵循的基本原则。文献[2]将EV用户的充电距离及路程用电损耗作为最小函数目标,以提高用户的使用满意度及经济效益,达到推广EV充电站的目的。文献[3]考虑了充电站的长期规划效益,但没有考虑短期内EV保有量变化的影响,没有对充电站的规划方案实现动态更新。文献[4]分析了充电站、分布式系统接入电网对配电系统稳定性的影响,建立了以总投资成本、检测服务、维护成本和失负荷成本最小为目标函数的配电系统、EV充电站与分布式储能复合规划模型,实现了对配电系统的动态规划和EV充电设施及分布式储能系统的选址。合理的充电站站址分布也方便今后检验检测机构开展检定校准服务工作。
考虑到目前国内EV用户保有量虽处于高速增长状态,但总体保有量仍处于较低水平,同时国产电池技术、充电桩基础设施等软硬件尚不完善,此时合理规划充电站的站址就显得举足轻重。因此,首先从充电站的点需求和流量需求两个方面考虑,构建以EV充电站设备建设者、EV用户和检验检测机构三者综合成本最小目标函数模型;其次,用Voronoi图结合粒子群算法的改进算法,实现对目标范围的自动寻优,获得了充电站站址的最终位置及检测服务范围。
1 点需求
点需求主要从宏观方面预测EV充电负荷的时空分布特征。首先,预测某规划地区未来EV的保有量,将该地区分成不同的区域,然后依据不同类型土地使用情况、停车分布特性、停车密度等来计算停车需求模型,得到该地区停车需求的时空分布,最终用来决定充电站及充电桩的数量。上述点需求的预测方法通常使用蒙特卡洛算法,该算法简单、清晰,易于实现。
2 流量需求
流量需求主要考虑EV车主驾驶习惯、天气、日期、EV状态、检验检测机构服务能力等多种因素的影响,结合出行者的出行起点与终点类型、出行线路图、形成所需电量,模拟出路网中总车流量来推算出充电需求,并以此为依据进行充电站站址的规划。与点需求相比,流量需求充分考虑了EV用户的实际需求、检验检测的服务能力及路网的实际运行情况,所以,流量需求分析更加具体、到位,能满足充电需求的动态变化。但该方法难以获取准确的概率分布模型。流量需求流程如图1所示。

图1 流量需求
基于流量需求预测充分考虑了出行者的出行特性、公路网的实际情况、检验检测机构服务能力、EV电池特性等,对充电需求时空分布的分析更加细致。采用蒙特卡洛抽样模拟、博弈论等思想获取概率分布模型。
3 充电站站址规划模型
根据流量需求和点需求的充电需求分布情况分析,综合考虑EV充电站设备建设者、EV用户和检验检测机构三者综合成本,建立目标函数:

式中:minC—— 充电站折算到每一年的最低费用;
N—— 区域内充电站的数量;
i—— 某个充电站(i= 1,2,3,…,i);
C1i—— 第i个充电站一次性投资折算到每年的费用;
C2i—— 第i个充电站每年设备维护费用;
C3i—— 第i个充电站电能损耗费用;
C4i—— 第i个充电站基础设施建设折算到每年的费用;
C5i—— 某个电动汽车用户成本;
C6i—— 第i个充电站检验检测机构服务成本
1)充电站的一次性投资年费用
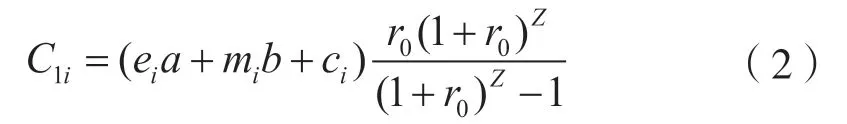
式中:ei—— 充电站变压器数量;
a—— 变压器单价;
ci—— 充电站基建成本;
mi—— 充电站的充电机数量;
b—— 充电机价格;
r0—— 充电站的贴现率;
z—— 充电站运行服务年限
2)充电站设备维护成本
充电站的维护成本主要包括设备耗材、设备折旧、工人工资、水电费等。常假设折算系数λ来计算充电站设备维护成本:
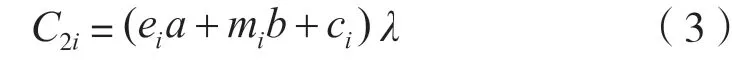
3)充电站电能损耗年费用

式中:CFe、CCa—— 变压器铁耗和铜耗;
Tv—— 充电站充电时长;
P0—— 电网电价(用户充电电价);
CL—— 线路损耗;
CD—— 充电机自身损耗;
ki—— 充电机的同时率
4)充电站基础设施建设年费用
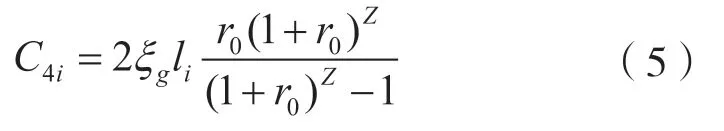
式中:ξg—— 每千米道路投资成本;
li—— 充电站连接到主干道的铺轨长度
5)EV用户成本
EV用户成本由充电往返途中的电量损耗成本和用户时间成本组成,其数学表达式为[5]
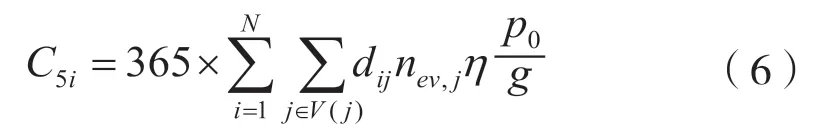
式中:V(j) —— 充电站服务范围内需求点集合;
j—— 充电服务范围内某一需求点;
dij—— 需求点j与充电站的距离;
nev,j—— 需求点j的EV数量;
η—— 充电用户需求比例;
g—— 单位电量可行驶里程
6)检验检测机构服务成本
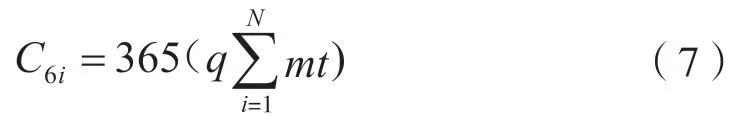
式中:q—— 检验检测机构时间服务成本;
N—— 需要提供检验检测服务的充电站数量;
t—— 检测某个充电站所花费的时间;
m—— 检测仪器折算到单位工作时间的成本
4 模型求解及仿真分析
4.1 模型求解
Voronoi图是俄国数学家G. Voronoi提出的,并将其扩展至高维空间。目前,Voronoi图已被广泛应用在几何信息相关的许多领域,如空间中求每一个多边形内的任意一点到本多边形母点的最短距离,这与充电站的选址思路相近,但Voronoi图却削弱全局寻优能力;而粒子群算法源于对鸟群捕食行为的研究,作为一种重要的优化算法已经成功地应用于函数优化、极值寻优、神经网络训练等领域。主要通过个体之间信息变化的共享,使整个种群的运动变成一种有序的推进状态。用xi表示每个粒子的位置,其结果对应一个规划问题的最优解;即

式中:d—— 粒子的维度,即充电站的数量;
xid—— 第i个粒子是否选择第d个充电站,其值为0或1,表达式为
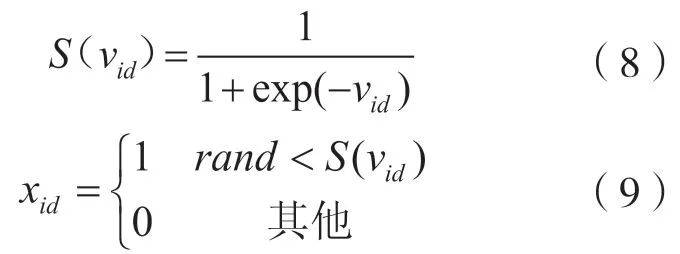
式中:S(vid) —— 位置xid取1的概率;
vid—— 粒子的速度
由式(9)可得,粒子位置为1的概率是S(vid),为0 的概率是1 -S(vid)。
但上述粒子群算法在实际应用中也存在一些问题,如:全局寻优能力较差、易出现早熟现象、收敛速度慢等。因此,对粒子群算法做如下改进:
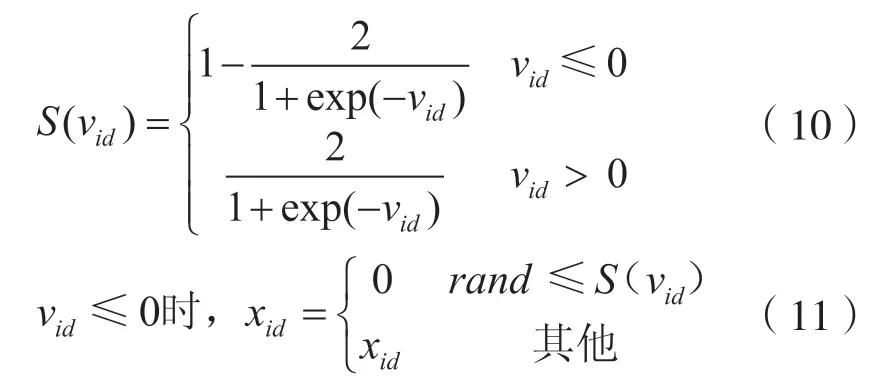

当粒子速度小于或趋于0时,粒子位置发生改变的概率为0;当粒子速度为0 时位置值不变;当粒子速度为正时,粒子位置可能变为1;改进后粒子群算法收敛速度加快,局部搜索能力增强。因此,采用Voronoi图结合粒子群算法进行模型求解,具体流程如图2所示。
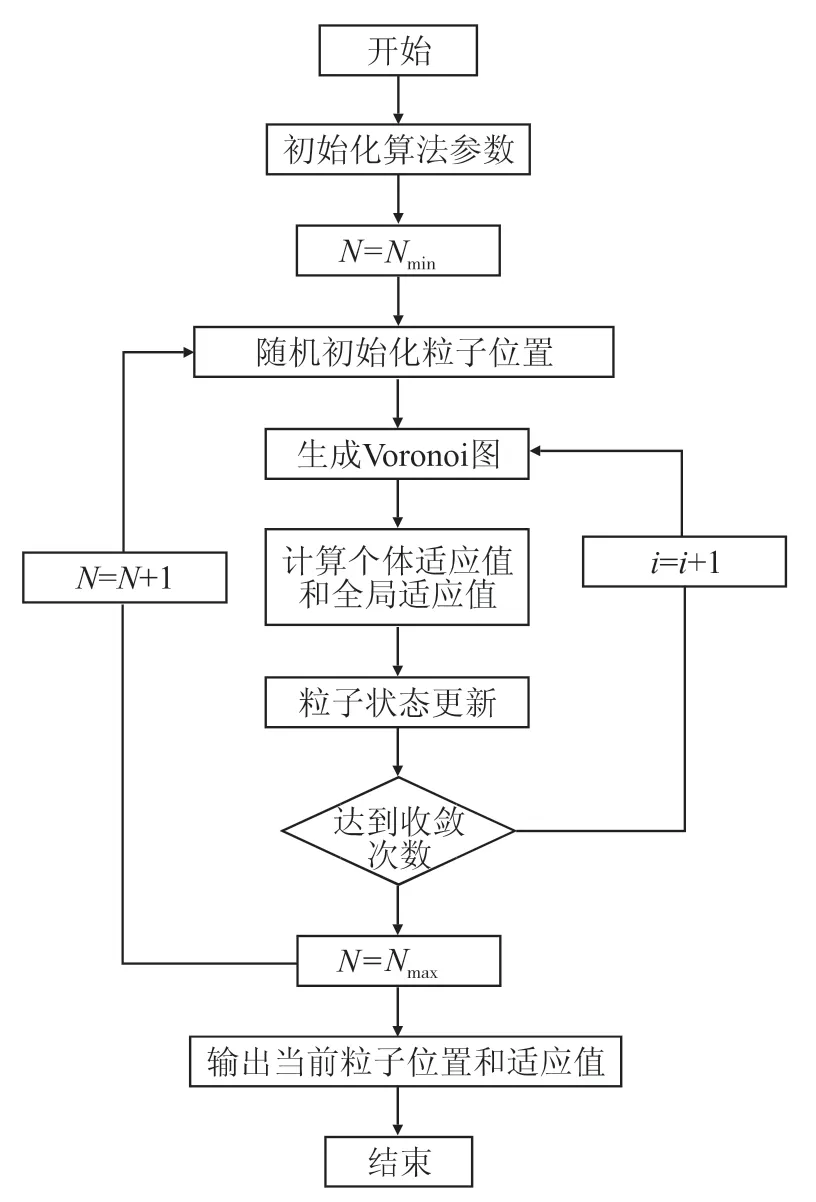
图2 算法流程
4.2 仿真分析
本文选定城市中比较有代表性的路段进行合理分析,路网节点36个,并以数字1~36号标注;通过使用MATLAB工具箱对提出的选址模型进行动态仿真,其相关参数参照文献[6],同时,预估该区域充电站数量为4~10个。
由图3可以看出,当该区域修建5个充电站时全社会的成本最小。图4根据充电站的规划得到具体的检测服务划分范围,充电站A辐射节点为1、2、10、11、14;充电站B辐射节点为24、25、26、34、35、36;充电站C辐射节点为15、16、17、21、22、23、27、28 ;充电站D辐射节点为3、4、5、6、7、8、9;充电站E辐射节点为18、19、29、30、31、32。图5为粒子群算法适应度收敛曲线,由于适应度下降速度快,进而更好地达到了收敛的效果。通过图3~图5,证明了所提出算法的可靠性,最终得到了合理的规划选择。

图3 充电站规划社会年总成本曲线
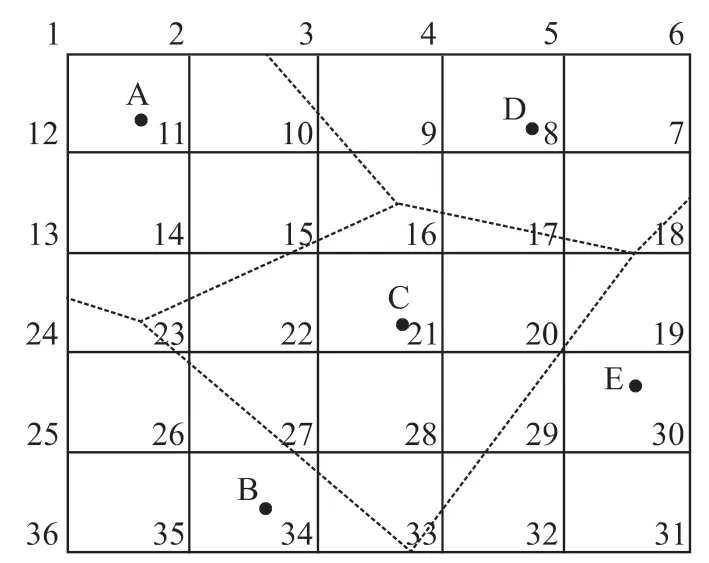
图4 充电站站址和服务范围
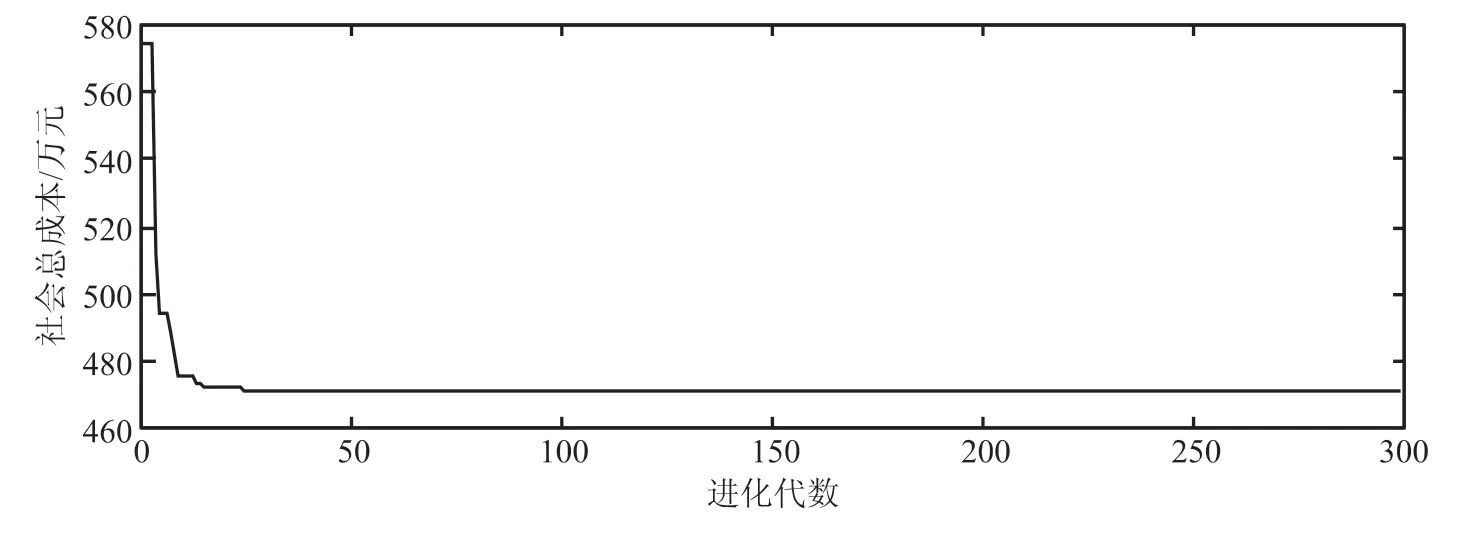
图5 算法收敛曲线
5 结语
构建EV充电站设备建设者、EV用户和检验检测机构的综合成本最小目标函数模型。通过构建改进的粒子群算法,结合Voronoi图对规划的路段进行仿真分析。结果表明,规划的充电站站址分布均匀,服务范围明确,社会总成本较低,对未来充电站站址的规划具有参考意义。后续可建立充电站的周期检定、出厂检测、安全巡检为一体的智能化检验检测实验室,满足政府监管和市场检测监测的需求。

