角度类仪器校准方法

王亚倩 经亚纯 路景飞 高同山 刘蕴 / 河北省计量监督检测研究院

0 引言

角度类仪器在各个行业中均有所应用，机械工作台、车床及切削工作台的水平位置检测，建筑工程设备的倾斜角检测及铁道系统铁轨水平度的检测等都离不开角度类仪器。而角度类仪器也由笨重复杂的框式水平仪以及条式水平仪等逐渐向数字化、轻便化、可量化的倾角仪转化。故本文以常见的数显倾角仪为例，探讨了计量行业中针对角度类仪器的测量方法，以供类似仪器的校准工作参考。

1 校准方法的比较

1.1 正弦规和量块组合（方法一）

正弦规是应用正弦原理，借助量块产生角度的一种计量器具[1]。将正弦规放置于平板上，被测数显倾角仪放置在正弦规上，调整数显倾角仪示值于零位。根据公式sinθ=d/L（θ为所需角度；d为量块尺寸；L为正弦规两侧圆柱中心距），计算出需要校准的角度所需量块尺寸。依次在正弦规的圆柱下放置相应校准点所需尺寸的5等量块，使正弦规与平板形成相应角度，逐个读取数显倾角仪示值，校准示意图见图1。数显倾角仪示值与正弦规产生的相应标准角度值之差为各校准点的示值误差。此种校准方法优点为所用标准器为一般计量机构均具备的正弦规与5等量块，便于测量的开展。缺点为使用该方法时，需要计算校准角度所对应尺寸的量块，但量块尺寸值有限，当校准某一具体角度值时，可能无法配置组合相应尺寸的量块，导致无法校准任意角度，具有一定的局限性。

图1 正弦规和量块组合校准数显倾角仪

1.2 光学分度头（方法二）

光学分度头是以光学度盘、圆光栅或圆感应同步器等为分度元件的测角仪器，在其圆周或者任意角度内可进行角度测量。校准数显倾角仪时，将数显倾角仪吸附在光学分度头中心轴附件上，置于水平位置。将光学分度头置于某一个整分度线处，倾角仪示值置于零位，按照校准角度转动光学分度头，倾角仪随之转动，如图2所示。倾角仪示值与光学分度头转动角度之差即为该点的示值误差。此种测量方法优点为可校准任意角度，准确度高、直观性强，无需过多计算，操作简便易行。不足之处为光学分度头仪器成本较高，检测过程中存在两次对线误差，人为因素引入的误差相对较多。

图2 光学分度头校准数显倾角仪

1.3 水平尺测量仪（方法三）

水平尺测量仪依据JJF 1085-2002《水平尺校准规范》[2]附录B专用检具技术要求定制而成，包括专用校准台、专用45°角尺、专用平面平行柱，分别可形成标准的0°、45°（135°）、±90°，如图3所示。校准时将数显倾角仪紧贴在水平尺测量仪的工作面上，以此校准相应点，如图4所示。使用水平尺测量仪校准数显倾角仪，优点为快捷直观，针对工作量大、要求不高的角度类器具的校准具有很大优势。缺点为此检具为专用设备，需定做，并对其平面度、平行度等有具体要求，且只能测量其固定的几个角度，无法满足其他特殊点的校准要求。

图3 水平尺测量仪

图4 水平尺测量仪校准数显倾角仪

2 三种方法校准数显倾角仪测量不确定度分析与比较

针对三种方法均能校准的45°校准点，以分度值为0.05°的数显倾角仪为例，分析三种校准方法校准的不确定度。

2.1 测量模型

Δα=αi-α

式中：Δα—— 数显倾角仪示值误差，（°）；

αi—— 数显倾角仪示值，（°）；

α—— 标准器产生的标准值，即45°

2.2 方差和灵敏系数

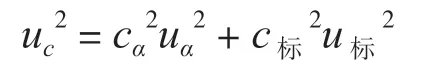
2.3 不确定度来源

三种校准方法的不确定度来源均为两大项，即被测数显倾角仪的重复性和所用标准器引入的不确定度分量。

2.3.1 正弦规和量块组合校准[3][4]

1）由测量重复性引入的标准不确定度分量u11

此分量可以通过连续测量形成的测量列得到，连续测量10次，得到测量列45.00°、45.05°、45.00°、45.05°、45.00°、45.00°、45.00°、45.05°、45.00°、45.05°。

单次测量的标准差

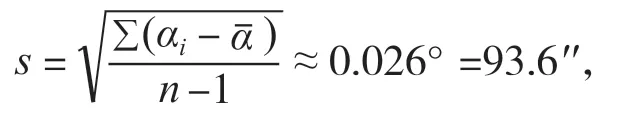
则u11=s= 93.6′′

2）标准器引入的不确定度分量u12

（1）正弦规两圆柱轴线间距误差引入的不确定度分量u121

查阅 JJG 37-2005《正弦规》检定规程可知，两圆柱中心距的偏差要求 ±1 μm，换算成角度偏差为±1.03′′。

（2）量块示值误差引入的不确定度分量u122

量块与200 mm的正弦规组成45°角，根据公式sinθ=d/L计算所需量块尺寸d为141.42 mm（选配量块组合方案：100 mm+40 mm+1.42 mm）。查阅JJG 146-2011《量块》检定规程[5]可知，100 mm量块长度最大极限偏差为±2.5 μm；40 mm 量块长度最大极限偏差为±1.6 μm；1.42 mm 量块长度最大极限偏差为±1.0 μm，总最大极限偏差为 ±5.1 μm，换算成角值偏差为±7.28′′。统计分析该分量接近均匀分布，包含因子为则

（3）平板平面度误差引入的不确定度分量u123

因（1）（2）（3）互不相关，可得标准器引入的不确定度分量测量重复性与标准器引入的不确定度分量彼此独立，互不相关，则合成标准不确定度为

扩展不确定度Uc1由合成标准不确定度uc1与包含因子k= 2得到

Uc1=kuc1= 2×93.7′′= 187.4′′ ≈0.052°

2.3.2 光学分度头测量

1）由测量重复性引入的标准不确定度分量u21

得到分量的方法如2.3.1中1）所述，u21= 93.6′′

总而言之，双源CT引导下，相较于普通CT而言，实施经皮穿刺活检术的安全性、准确性更高，随着现代医疗设备的不断完善和更新，双源CT引导下对胸腹部占位性病变患者实施经皮穿刺活检术，必然会在临床中进一步得到广泛应用。

2）标准器引入的不确定度分量u22

（1）光学分度头示值误差引入的不确定度分量u221。校准所用光学分度头示值误差为6′′，半宽区间为3′′，按照均匀分布，包含因子为

（2）校准过程中对线误差引入的不确定度分量u222。对线误差为±1′′，按照均匀分布，包含因子为校准过程中存在两次对线误差，故

扩展不确定度Uc2由合成标准不确定度uc2与包含因子k= 2得到

Uc2=kuc2= 2×93.6′′= 187.2′′ ≈0.052°

2.3.3 水平尺测量仪测量

1）由测量重复性引入的标准不确定度分量u31

得到分量的方法如2.3.1中1）所述，u31= 93.6′′

2）标准器带来的不确定度分量u32

45°检具引入的不确定度分量u32。45°检具的角度误差为20′′，均匀分布，故

测量重复性与标准器引入的不确定度分量彼此独立，互不相关，则合成标准不确定度为

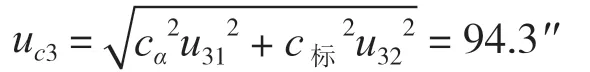
扩展不确定度Uc3由合成标准不确定度uc3与包含因子k= 2得到

Uc3=kuc3= 2×94.3′′= 188.6′′ ≈0.052°

综上所述，三种测量方法的不确定度分量见表1。

表1 标准不确定度汇总

对于分辨力0.05°数显倾角仪而言，示值最大允许误差为±0.2°，以上三种测量方法评定其示值误差测量结果的扩展不确定度U= 0.052°，k= 2，满足U≤1/3×MPEV判定准则的要求，因此，可判断上述三种校准方法均合理可行。同理可得，分辨力为0.01°的数显倾角仪，示值最大允许误差为±0.05°，其不确定度用上述三种方法计算可得U= 0.016°，k= 2，均满足计量要求。且由相关数据可知，不确定度分量主要由测量重复性组成，标准器引入的不确定度分量可控制在一定范围内，因此，校准更高准确度角度类计量器具时，均可用此三种方法。

3 结语

在计量工作中，经常遇到角度类计量器具的校准检测，本文通过常见的数显倾角仪校准，分列了三种常见、可行的方法，结果表明，均可满足计量要求。计量工作人员可根据实际情况选择最便捷、适合的校准方法。另外，可参考本文选择其他标准器进行校准，例如，利用角度块也可进行数显倾角仪的校准，也比较方便可行。