基于切削原位成像法的45钢塑性本构参数辨识*

陈小琦，张 可，聂广超，张小明

（1.中南大学，长沙 410083； 2.华中科技大学，武汉 430074）

切削过程实质上是在外力作用下，材料产生剧烈塑性变形然后切屑-工件分离的过程。该过程是个极为复杂的物理过程，为研究其切削机理，对切削加工过程进行预测，传统的解析方法已不适用，而直接进行试验比较耗时耗力，且成本高[1–3]。随着有限元技术的发展，有限元切削仿真在难加工材料切削研究中发挥着越来越重要的作用。有限元仿真计算结果的准确性与材料本构模型参数的准确性直接相关，因此材料本构模型参数辨识成为切削仿真工作的基础。

目前存在多种本构模型描述应力与应变、应变率、温度之间的关系[4-5]，其中Johnson–Cook（J-C）本构模型在金属切削中应用最为广泛。国内外学者对于J–C 本构模型的参数识别进行了大量的研究，鲁世红等[6]通过SHPB 试验结合自适应遗传算法对TC4 钛合金J–C 本构模型参数进行了辨识，应变率达到的范围为102～104s–1，与实际切削过程应变率差距较大。Tounsi等[7]基于应变率的分段线性分布确定了一种分析模型，通过一次切削试验就获得足够的数据量，通过使分析模型预测的物理量与试验测量值相匹配辨识本构模型系数。Özel 等[8]通过试验测得切削力与切屑厚度，应用Oxley 滑移线场逆分析来计算J–C 本构参数，该模型对剪切带上的平均温度计算做出了改进。Klocke等[9]基于有限元与试验对比的方法研究了非稳态切削过程，将锯齿状切屑与切削力作为研究对象辨识本构参数。

从上述关于J–C 材料本构参数识别的文献综述中可知，SHPB 试验可以获得高应变率下的本构参数，但对于金属切削产生的应力状态范围、应变和应变速率水平来说，此种试验方法还相差较大；切削试验是获得本构参数的较为有效方法，但缺乏对应变和应变率分布定量分析的试验验证。针对上述问题，引入原位成像技术[10–12]来获得切削区域的变形场，通过数字图像相关技术（DIC）分析，可获得切削区域的应变及应变率分布。本文搭建了一套原位成像切削试验平台，在不同切削条件下对45 钢（美标AISI 1045）进行正交切削试验，基于DIC 技术以及正交切削的分析模型，提出了一种新的J–C 本构参数辨识方法。

1 试验过程

1.1 试验平台

本次试验所搭建的一套原位成像试验装置如图1所示，其中主要模块包括：双帧相机及镜头、LED 灯、接触开关、测力仪、脉冲信号同步触发模块、信号采集系统等。

图1 原位成像试验平台Fig.1 In-situ imaging experimental set-up

试验所配备的双帧相机为PCOPixelfly USB，可达到的最小帧间距为1μs，分辨率为1392×1040，配合使用的镜头为Navitar X12 变焦镜头，7 倍放大的主镜头与2倍放大的自适应器，能在1～14 倍间调整整体放大倍数。采用的压电三向测力仪的型号为KISTLER 9257B。试验过程中通过控制脉冲信号来调节LED 灯的出光时间以达到调节帧间距的目的，同时通过脉冲触发相机拍照及测力仪采集力信号。

1.2 试验材料及参数

45 钢是一种优质中碳结构钢，具有良好的综合力学性能。45 钢制成尺寸为40mm×25mm×2mm 的片状工件，由相应夹具固定在主轴上随主轴旋转进行正交车削试验。试验之前需将工件的一面打磨，使其表面颗粒分布均匀且无规律，以获得高质量图片用于DIC分析。

切削刀具选用SECO TPUN160308 涂层刀片，刀杆型号为Sandvik CTFRL2525M16，装配后切削刀具前角6°，后角5°，刃倾角0°。0°刃倾角实现正交车削，保证工件变形满足平面应变条件。刀具圆角处需磨成一个平面，让相机得以聚焦。为了获取更多切削条件下的试验参数，在相机帧率允许条件下，切削速度在30～300m/min范围内选取9 级。考虑到相机视野大小与图像清晰度，切厚选择为0.1mm、0.15mm 和0.2mm 3 种，具体切削试验参数如表1 所示。

2 本构参数辨识模型

J–C 本构模型表达式为：

表1 正交车削试验参数Table 1 Orthogonal cutting parameters

其中，σ、ε、ε.、T分别表示流动应力、等效应变、等效应变率和切削温度，A、B、C、n、m分别是材料的屈服强度、应变硬化模量、应变率硬化系数、应变硬化指数和热软化指数。此外，ε.0 为参考应变率，设置为1s–1；Tm为材料的熔点，所用材料为1459℃；T0为室温，25℃。

式（1）中A、B和n可以通过准静态拉伸或压缩试验获得，表示的是材料的应变硬化性能，较为容易获得。因此，本次辨识的主要目标是通过DIC 分析及测量切削力对应变率硬化系数C及热软化系数m进行优化辨识。

本构参数辨识算法的输入为J–C 本构参数及切削参数，输出为优化的C、m，算法流程图如图2 所示。其中，V为切削速度；h为变形切厚；γ为刀具前角；β为刀具后角；w为工件宽度；LS 为least square（最小二乘法）。

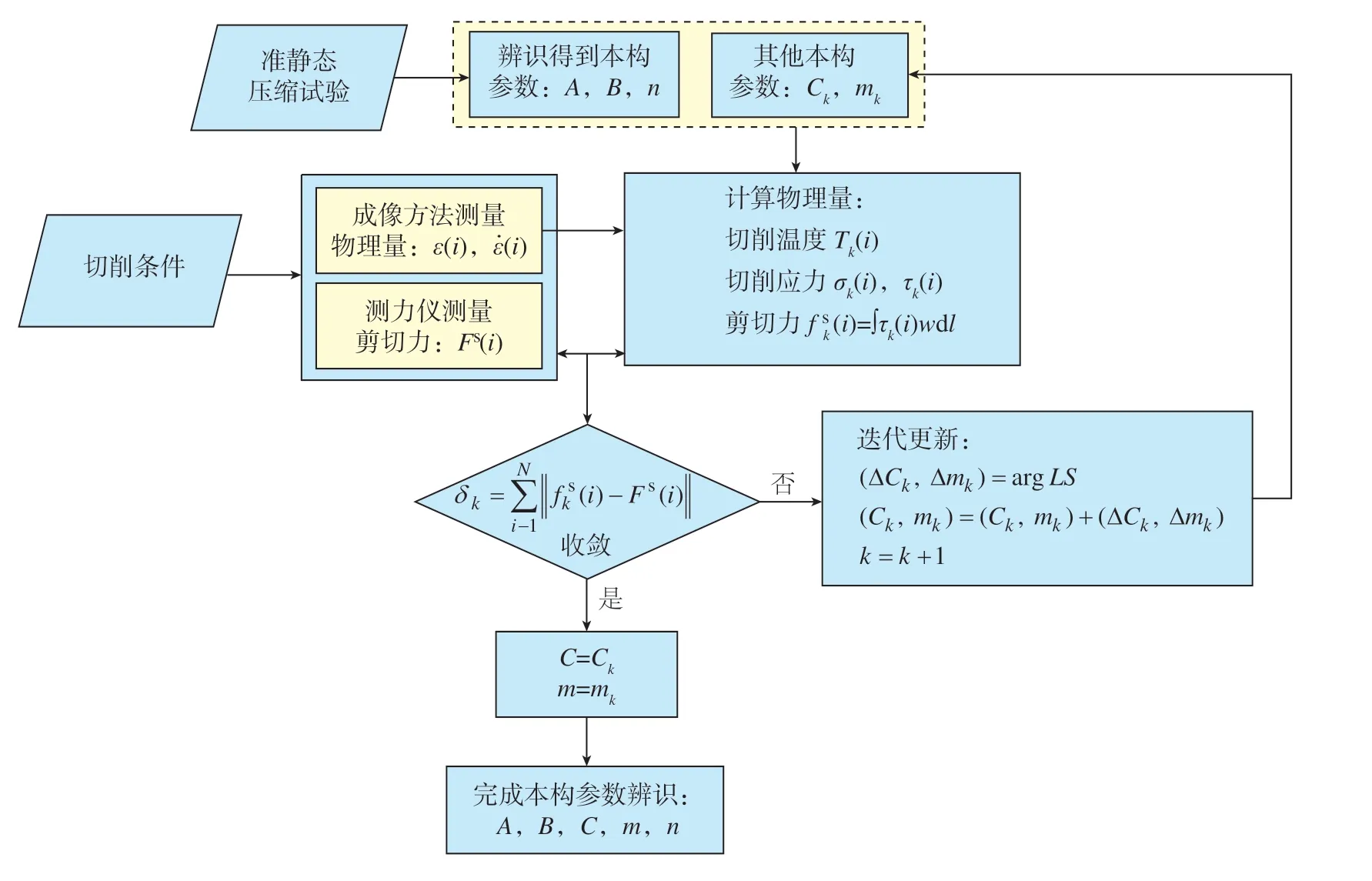
图2 本构参数反向辨识算法流程图Fig.2 Algorithm flowchart of proposed approach for inverse identifying the constitutive model coefficients

2.1 原位成像试验获取应变率场

通过原位成像试验获得第一剪切变形区相隔数微秒的两帧图像，称为参考图像和当前图像，通过DIC 方法[13]将参考图像中的每个像素点，根据其邻域信息，在当前图像中找到对应的点，由像素点间的位置变换关系得到位移，于是得到位移场。位移场除以帧间距得到速度场。其中，两组试验参数（条件1为V=40m/min，h=0.1mm，条件2为V=150m/min，h=0.2mm，后文简称条件1 与条件2）获得的速度场如图3 所示。

位移场通过最小二乘平面拟合算法进行平滑处理，拟合平面梯度信息包括其中，LSF 表示最小二乘拟合，（ui，vi）表示点（Xi，Yi）处X、Y方向的位移分量。进一步计算等效应变率：

其中，tint表示帧间距。得到两种切削条件下的等效应变率如图4 所示。可见在切削速度为150m/min、切厚为2mm 的情况下，剪切带上最大应变率分别能达到2×104s–1，当切削速度达到300m/min 时能达到105s–1。根据剪切带上应变率最大，可以从应变率场上在第1 剪切变形区辨识得到剪切带。

图3 X方向与Y方向速度场Fig.3 Velocity fields along X and Y directions

图4 等效应变率场Fig.4 Equivalent plastic strain rate fields

基于稳态切削假设，粒子运动的迹线与瞬态下的流线是重合的[14]。根据速度场追踪粒子的流线并沿着流线对应变率积分，可以得到应变场如图5 所示。

2.2 剪切力计算

切削理论模型如图6 所示，假设剪切带AB的应力状态为纯剪切状态。因此剪切力可以由合力投影到剪切带上计算得到：

剪切带AB的剪切力FS为：

其中，τ为沿AB的剪应力，w为切宽2mm，σ为通过式（1）计算的平均应力，对其计算的另一要点即对剪切带平均温度的计算。

本次试验使用的45 钢的A、B、n通过准静态压缩试验获得为：A=507MPa，B=507MPa，n=0.28。其他参数C和m根据文献[15]预设为C=0.064，m=1.06。

图5 等效应变场Fig.5 Equivalent plastic strain fields

图6 第1剪切变形区几何模型Fig.6 Geometrical model of PSZ

2.3 温度计算

基于第1 步中获得的等效应变及等效应变率，结合Oxley 模型的延伸模型[16]，根据剪切过程中塑形功部分转换为温升来计算剪切带上的平均温度TAB：

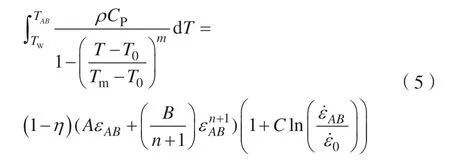
式中，TW为工件的初始温度，这里视为室温25℃；ρ为材料的密度7800kg/m3；CP为比热容（460J/（kg·℃））；εAB.分别为剪切带上的平均应变与平均应变率；η为热分配系数，通过经验公式计算：

其中，φ为剪切角，通过等效应变场辨识剪切带得到；RT为无量纲热值，RT=ρCPVh/λ，V与h为切削速度与未变形切厚，λ为材料的热传导系数42W/（m·℃）。

2.4 参数优化过程

优化目标为C、m，通过试验获得的剪切力与计算获得的剪切力对比来更新。通过DIC 分析，对式（4）按照像素点进行离散，其中Δl是相邻像素点间的距离，j为剪切带上的第j个像素点。

从df(i)=fS(i)–FS(i)，i为试验组号，可得：

C与m通过迭代更新为：

优化算法的代价函数为：

其中，N表示为试验结果组数；k为迭代次数；FS为试验通过测力仪获得的剪切力，收敛准则为取阈值为∈=0.5%。

3 结果分析与讨论

3.1 试验结果

根据表1 列出的切削参数表进行正交车削试验，每组参数重复试验3 次；将成像法得到的应变、应变率以及温度通过本构方程计算得到的剪切力与由测力仪测得的剪切力相匹配对本构参数进行优化，剪切力的迭代过程对比如表2 所示；相应的C和m的迭代过程如表3 所示；最后辨识得到的本构参数如表4 所示。

表2 剪切力迭代过程Table 2 Iterations of shear forces N

表3 本构参数C和m迭代过程Table 3 Iterations of C and m

表4 45钢J–C本构参数Table 4 Constitutive parameters of 45 steel

3.2 有限元仿真结果对比

对示例的两组切削参数进行有限元仿真，仿真使用切削专用有限元软件Deform，描述塑形行为的J–C本构参数使用辨识结果，如表5 所示；仿真得到应变场如图7 所示，应变值、应变分布与试验测得结果相近。

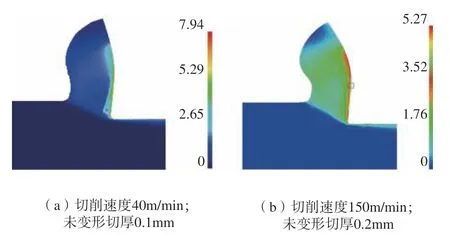
图7 有限元仿真获得的等效应变场Fig.7 Equivalent plastic strain fields by finite element simulation

此外，表5 给出试验中测力仪测量得到的切向力FC、推力FT以及基于成像方法测量的应变与应变率通过数值方法计算出的剪切带上的平均温度和有限元仿真得到的对应物理量的对比，发现有较好的匹配度，这些结果显示本方法所辨识出的本构参数具有可靠性。

表5 试验测量值与有限元仿真对比Table 5 Comparisons of measurements with finite element simulations

4 结论

本文基于切削原位成像技术提出了一种新的方法对45 钢塑形本构参数进行辨识，通过正交车削试验与有限元仿真得出以下结论：

（1）在正交车削试验中，通过双帧相机和DIC 算法可以有效测得切削过程中第1 剪切变形区的应变和应变率，测量范围大于传统机械测试所能测试的范围。且该方法主要受设备限制，更换更高帧率相机及相应光照系统即可实现更高应变率测量。

（2）切削加工温度的测量是一项难点，本文通过数值模拟的方法计算剪切带上平均温度，与有限元仿真温度对比，误差在10%以内。如果能通过红外测温、双色测温或其他方法实现对剪切带上温度分布的测量，能得到更符合实际情况的结果。

（3）通过将成像方法得到的剪切力与测力仪测量值进行匹配，经过最小二乘方法优化实现了对45 钢塑性本构参数的辨识，辨识结果通过有限元仿真得到验证。