热障涂层热物性研究进展*
金圣皓,王博翔,赵长颖
(上海交通大学,上海 200240)
随着效率和功率需求的不断提高,航空发动机、燃气轮机不可避免地向着高工作温度、高推重比和高流量比的方向发展[1]。在高温工作条件下,燃气轮机工作叶片将承受较大的热负荷,此时热防护问题将变得至关重要。热障涂层(Thermal barrier coatings,TBCs)是一种具有良好热力性能的复合材料,其具有导热率低、抗热冲击及抗高温腐蚀的优良性能,这些性能使得该结构能够实现良好的隔热效果,降低基底材料的热流密度和工作温度。目前TBCs 已被广泛用于燃气轮机中高压导向叶片、涡轮转子叶片、喷嘴以及燃烧室腔体壁面等热端部件的高温防护上。
热障涂层应用于燃气轮机热防护始于20 世纪50 年代,经过半个多世纪的发展,目前TBCs 已具有一些固定的结构和成熟的制备技术。在结构方面,现今常见的热障涂层主要包括双层TBCs,多层TBCs 和功能梯度TBCs[2]。其中双层TBCs 是目前应用最为广泛的结构,由于制备技术相对成熟。目前该结构已广泛应用于工业生产[2]。双层TBCs 结构主要由陶瓷-金属两层组成,其中顶部的陶瓷涂层起到主要隔热作用,底部的金属黏结层则起到防止顶部隔热涂层从合金基底脱落及抗高温氧化的作用;多层TBCs 则是在双层结构的基础上加入了封阻层、隔热层等提高隔热性能的结构,但由于这种结构对TBCs 的抗震性能改善不大,且制备工艺复杂,因此在实际生产应用中并未广泛应用;功能梯度TBCs 则是一种由先进的材料复合技术制备的性能和功能沿厚度方向呈梯度变化的材料,这种新型的TBCs 结构能够较好地解决传统双层TBCs 存在的层间热膨胀系数和弹性模量不匹配的问题。且相比于传统TBCs而言,功能梯度TBCs 具有更强的抗震性能。但由于制备技术较为复杂,因此功能TBCs 涂层目前还处于试验室研究阶段[2]。在制备技术方面,目前热障涂层结构的主要制备工艺为等离子体喷涂技术(PS)和电子束物理气相沉积技术(EB-PVD)[3]。等离子喷涂法是最早用于制备热障涂层的工艺,其加工出的热障涂层具有层状微结构,该方法具有成本较低的优势[3],但制备出的热障涂层由于存在夹杂、微裂纹、孔隙率高等缺陷导致抗震性等力学性能较差。电子束物理气相沉积技术是一种利用电子束的能量加热并气化材料,进而将其沉积到基体上形成涂层的技术,其加工出的热障涂层具有柱状微结构。相比于等离子体喷涂法而言,电子束物理气相沉积技术制备的热障涂层具有更高的热循环寿命和更强的结合力[2]。但存在制作成本高、沉积效率低的劣势,尤其由该方法加工造成的柱状微结构是平行于热流方向的,这会削弱热障涂层结构对导热和辐射热流的隔热功能。除了上述两种较为成熟的传统方法,近年来在热障涂层的制备技术方面还发展出了激光熔覆法和冷喷涂法两种新型方法[2]。使得热障涂层制备工艺更加完善,涂层性能显著提升。
作为一种工作在高温下的隔热材料,隔热性能是热障涂层最重要的性能指标之一。而对于热障涂层而言,起到隔热作用的主要是顶层陶瓷材料,因此顶部陶瓷涂层材料的热物理性能直接决定了其热力学性能的优劣。目前,氧化钇部分稳定的氧化锆(YSZ)这种陶瓷材料由于在高温条件下具有低的导热率(1000℃,致密状态下为2.3W/(m·K))和较高的熔点(2700℃)等利于高温隔热及高温作业的优良热物理性能而被广泛用于热障涂层领域[3]。随着燃气轮机工作温度需求的提高,一些具有更优良高温热物理性能的材料,如稀土氧化物掺杂的YSZ[4]、锆酸盐[5]等也被应用于TBCs 陶瓷涂层。除此之外,陶瓷材料内部孔隙大小、孔隙率、孔隙形状、孔隙朝向、晶界、掺杂缺陷等微结构特性都会直接影响到TBCs 陶瓷材料内部的声子、光子散射,从而直接影响到热障涂层的隔热性能。上述方面都为热障涂层的传热领域提供了广泛的研究空间。
目前,如何有效提高热障涂层的隔热性能是热障涂层领域的热点研究问题。本文重点归纳总结了近10年热障涂层领域对导热和辐射两大传热特性的相关理论、试验研究。在理论方面,介绍了热障涂层材料从宏观尺度到微观尺度的导热、辐射研究理论并总结了不同尺度下热障涂层材料传热特性的理论研究。在试验方面,详细总结了对于不同材料,不同结构热障涂层导热、辐射特性的相关试验研究。
热障涂层的导热研究
在过去的几十年中,对热障涂层材料导热特性和隔热性能的研究取得了较大的发展。在材料方面,目前大多数相关研究基于最常用的氧化钇部分稳定的氧化锆(Yttriastabilized zirconia,YSZ)材料。而为了满足燃气轮机温度工况不断增加的发展需求,一些具有更高综合性能的新型材料如掺杂YSZ、锆酸盐的导热特性和隔热性能也逐步得到研究。目前,大多数对热障涂层导热性能的研究集中于导热系数的测量。随着计算能力的发展,有限元法,格子玻尔兹曼法,分子动力学模拟等数值方法也被大量应用于热障涂层导热特性的研究。
1 热障涂层内的导热机理
热障涂层这类多孔材料中的热传导主要由YSZ 材料内的声子导热,以及气孔内的气相导热及Knudsen 传热组成[6]。晶体中主要存在两种热传导机制,分别是电子导热和声子导热(即晶格振动传热)[7]。对于热障涂层而言,在中高温范围内材料的热传导过程主要由声子的输运来实现。在Debye 理论的基础上,根据声子动力学理论,晶格振动对热传导的贡献(κl)可表示为:

其中,Cl为材料单位体积晶格比热容;νg为声子速度;l为声子平均自由程。由于Cl和νg的大小主要受材料种类的影响,因此对于选材基本固定的热障涂层而言,Cl和νg对其导热性能影响不大。对热障涂层导热系数影响最大的参数为声子平均自由程l,声子平均自由程大小与声子散射过程有着直接的关系,而声子的散射过程又与材料的微结构紧密相关。声子的散射过程一般可以分为声子-边界散射、声子-缺陷散射和声子-声子散射3 大类。根据Matthiessen规则,3 种散射过程对声子的平均自由程的影响可量化表示为:
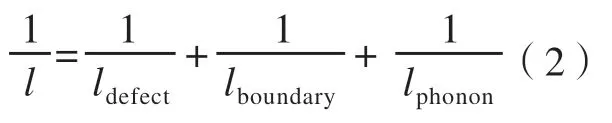
其中,ldefect、lboundary和lphonon分别表示缺陷、边界及其他声子对声子平均自由程的影响。作为一种多孔材料,热障涂层内部存在大量的缺陷及边界结构,且不同的加工方式也会导致热障涂层具有完全不同的微观结构,因此热障涂层内部的微结构参数必然会在影响其内部分子平均自由程大小的基础上极大地影响涂层的导热性能。
关于气孔内部的气相导热,一般可用特征长度为dν的受限制气道内气体的导热系数Kg模型计算热障涂层中孔隙内部气体的导热系数,具体可由下列经验公式进行计算[8]:
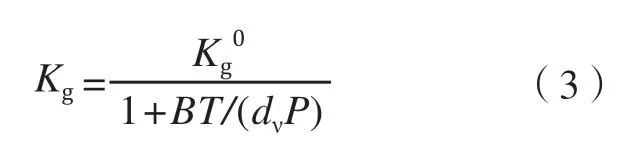
其中,P为气体压力;T为气体温度(绝对温度);为不受气道几何空间限制的自由气体的在相应温度下的导热系数;B为气体常数,其大小与气体种类、气道固体表面材料、表面粗糙度以及气相-固相相互作用有关。实际上,气体压力P和气体温度T的大小会直接影响到孔内气体的分子平均自由程λ的大小,从而对气孔内的气相导热及其导热系数有显著影响。在常压条件下,分子平均自由程λ大于气孔的特征长度dν,此时气孔内发生Knudsen 传热,该效应会导致孔内气体的导热系数Kg远低于同温度下自由气体的导热系数,且Kg几乎不随温度变化,不会像自由空间气体导热系数Kg0一样随温度升高而增大,利于热障涂层的整体隔热性能。但在热障涂层工作的高压条件下,分子平均自由程会小于或远小于气孔的特征长度,此时孔内气体的导热系数会大于常压下的孔内气体导热系数,其导热系数表现出随温度的升高而增大的性质,且数值随着压力的升高而不断趋近于自由空间中的气体导热系数,这会对热障涂层的整体隔热特性造成一定的不利影响。
目前,对热障涂层导热特性的研究主要集中于内部声子导热、内部边界导热以及微结构结构参数对两种导热过程的影响3 个方面,这部分的相关研究将在下面的热障涂层导热特性研究部分详细介绍。
2 热障涂层导热特性的理论研究
在热障涂层导热特性的理论研究方面:对于传统的YSZ 材料,多数研究应用基于热扩散方程的等效介质模型和有限元法对该材料的导热特性进行研究。而对于具有微纳米量级微结构的TBCs 材料,宏观热扩散方程不再适用,因此多数研究采用基于玻尔兹曼输运方程的格子-玻尔兹曼法或分子动力学法对这些材料的导热特性进行研究。
2.1 基于宏观傅里叶导热定律的理论研究
傅里叶导热定律是研究物体内热传导最为常用的理论。该理论在局部热平衡假设的基础之上,建立起了导热热流和温度梯度之间的数量关系:

其中,λ为材料的导热系数。进而基于该理论,对于一个微元控制体使用能量平衡进行分析,即可获得关于物体内温度分布T(x,y,z,t)的偏微分方程,即热扩散方程:
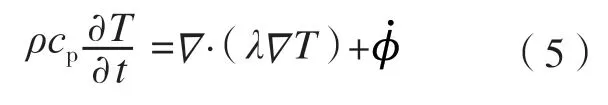
其中,t为时间项;ρ为材料密度;cp为材料比热容; 为体积热量产生率;·为散度算子;为求向量场的偏导数。
对于宏观导热问题,由于局部热平衡假设能够得到满足,因此傅里叶导热定律是始终成立的。所谓局部热平衡假设,就是假设粒子或物理量的分布函数f离平衡态不远,从而可以满足关系式∂f/∂r≈∂f(eq)/∂r,其中f(eq)为平衡态下的分布函数[9]。通过求解基于傅里叶导热定律的热扩散方程即可准确求解物体内部的传热问题。通常在给定了相关导热问题的边界条件后,就可以通过解析法或数值计算法获得热扩散方程的解。
在热障涂层导热问题研究这一方面,研究者们最初大多基于傅里叶导热定律建立相应的等效分析模型,以预测相关材料的导热系数[10-13]。近年来随着数值计算技术的大幅发展,基于求解热扩散方程的有限元法逐渐成为了研究热障涂层材料导热特性的主要方法[14-17]。
(1)等效介质模型。
热障涂层的导热问题可以划归到多孔介质导热问题的范畴内,对于多孔介质而言,早期的一些研究一般都通过建立等效分析模型计算等效导热系数来简单研究热障涂层内部的导热问题及微观结构对导热性能的影响。作为多孔材料,热障涂层的导热系数可通过复合材料的Eshelby 方法等效导热模型来进行简单计算[9-10]:
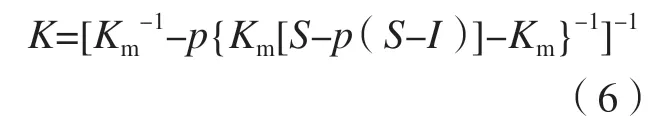
其中,p为椭球型孔隙的体积分数;Km为介质材料的导热系数;S为Eshelby 张量,I为特征张量。然而Clyne 等[9]经过计算发现,该模型对TBCs 导热系数的运算结果往往会比实际偏大,这主要是由于该模型不能够充分地描述热障涂层内气孔的复杂几何结构。除此之外,Ravichandran 等[11]通过把层状间的界面简化为“界面传热系数”,建立了TBCs 等效导热系数的计算模型。模型研究了孔、界面、裂纹等对等效导热系数的影响。但该模型只考虑了孔隙对导热系数影响的整体效果。
为了更加准确地计算热障涂层材料的等效导热系数,Golosnoy 等[12]发展了一种基于较为简单的“桥接”结构的模型用于对热障涂层的孔隙结构进行模拟,该模型将热障涂层中的热流分为两类:一类是通过模型“接触桥”结构的漏斗形热流;另一类是通过模型气孔部分的直线热流。该种模型可做到将TBCs 的微观结构参数考虑在内,并得出更加准确的等效导热系数计算结果。
(2)有限元法。
然而,由于热障涂层中存在复杂的孔隙、裂纹等微观结构,不可能仅仅用简单的分析模型得出其等效导热系数。近十年来,随着计算机计算能力及有限元法的发展,一些研究应用有限元分析法对YSZ TBCs 内的导热过程进行建模研究[13-16]。有限元分析法(FEM)是一种用于求解偏微分方程(PDE)近似解的数值技术。所谓有限元法,就是通过在空间维度上对实际研究的连续体进行特定的离散化,使连续介质离散为若干有限大小的单元体,最终使具有边界条件的PDE 简化为代数方程组并用于求解的数值方法。有限元法是一种非常强大的数值计算方法,目前的很多知名商业软件,如COMSOL、ANSYS 等都是基于有限元法建立的。这使得有限元法的应用变得十分简单方便。相比于传统的等效分析模型而言,有限元法具有不需人为对物理问题进行建模,操作方便,求解精确的优势。对于一般连续介质,只要几何模型符合实际,网格划分合理,就能够算出比较符合实际情况的结果。因此有限元法是一种较为适合研究热障涂层的微观结构对导热性能影响的数值方法。目前研究者们主要通过有限元分析法研究传统的YSZ TBCs 内的微观结构对其导热特性的影响。如Lu 等[13]通过SEM 图获得了YSZ TBCs 的微观结构,建立了包含实际多孔结构和splat 界面分布信息的有限元模型,结果发现该模型可以正确预测等离子体喷涂TBCs 的各向异性导热性能。Wang[14]基于有限元法模拟分析了YSZ 材料中孔隙的大小和几何特性对其导热特性的影响,并基于新颖的计算微观力学方法(CMM 法)模拟了TBCs 内部的传热过程,计算了等效导热系数。文献[14]还建立起了不同种类缺陷对应的计算模型,最终建立了TBCs 有效导热系数与缺陷方向角,缺陷体积分数及缺陷形状系数的函数关系。模拟结果发现,YSZ材料的隔热性能会随着孔隙大小,孔隙体积分数及垂直于厚度方向的孔层数量增加以及两相邻气孔间的间距减小而增加。Shen[15]用数值方法研究了YSZ 材料的孔隙及裂纹对其有效导热系数的影响,基于能量守恒原理建立了相应的数学公式用以揭示缺陷各参数与有效导热系数间的关系。文献[15]应用有限元法及严格的分析计算法定义了缺陷参数对有效导热率的影响系数,首次定量地揭示了孔隙半径及裂纹长度对有效导热系数的影响。计算结果发现,相对于任何单个缺陷,最长的横向裂纹对沿喷涂方向的有效热导率起着最重要的作用。Wang[16]基于几种不同的界面热阻(ITR)模型,通过TBCs的真实微结构SEM 图进行建模,在此基础上采用有限元方法模拟了具有不同界面特性的YSZ 材料的传热行为,并用CMM 法模拟了涂层内部不规则界面处的传热过程,最后通过试验验证了计算模型的有效性。结果发现,随着界面面积的增加,YSZ材料的隔热效果将增强,且涂层的界面粗糙度对TBCs 的有效导热率也有非常重要的影响。
虽然有限元法具有技术成熟、操作方便的优势,但热障涂层实际微结构十分复杂,这会导致有限元法在保证复杂界面的连续性上存在耗费大量计算时间的问题,且随着热障涂层材料的发展,目前很多热障涂层都具有微纳米尺度的结构,而在微观尺度上,由于尺寸效应的存在,有限元法基于的连续性假设和宏观傅里叶导热定律已不再成立。因此有限元法对TBCs 的研究目前只能局限于宏观尺度领域。
2.2 基于玻尔兹曼输运方程的理论研究
随着热障涂层材料的不断发展,其内部微结构的特征尺寸也在不断地缩小,当特征尺寸达到微纳米量级时,材料内部的声子平均自由程可能会大于或等于特征尺寸,此时局部热平衡假设将会失效(假设条件 ∂f/∂r≈∂f(eq)/∂r不再成立),因此宏观傅里叶导热定律及基于其建立的热扩散方程也不再成立。因此需要通过新的理论来研究介观和微观尺度热障涂层的导热问题。玻尔兹曼输运方程法即是一种可解决上述问题的良好理论方法。
(1)玻尔兹曼输运方程。
玻尔兹曼输运方程(BTE)是一种可用于描述非热力学平衡状态的热力学系统统计行为的偏微分方程,由著名物理学家Boltzmann 在研究气体动力学时建立。相比于热扩散方程而言,该方程不受局部热平衡假设的限制,可良好地应用于小空间尺度和小时间尺度下的热力学问题。该方程具有十分广泛的适用性,目前已被推广到研究固体中的声子、电子传递。
具体而言,玻尔兹曼输运方程是关于各种粒子或物理量分布函数的偏微分方程,其一般表达式如式(7)所示[17]:
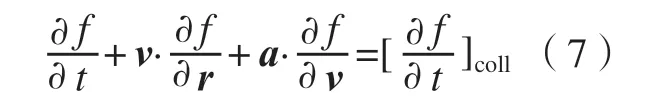
其中,f为粒子或物理量的分布函数;为分布函数随时间的变化项;为分布函数的扩散项;其中v表示速度;为分布函数f随笛卡尔空间坐标r的变化梯度;为外力项;其中a表示加速度为分布函数f随速度项v的变化梯度;则为碰撞项,碰撞项的形式十分复杂,通常可以用式(8)表示:
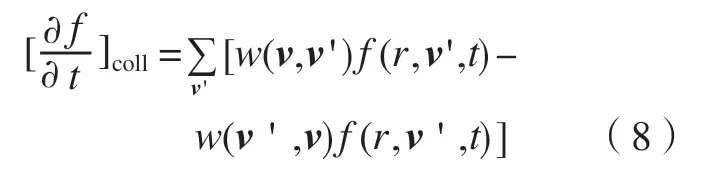
其中,w(v,v') 为散射概率。碰撞项实质上是一个复杂的非线性积分,难以进行求解,这使得BTE 方程的应用受到限制。
为解决这一问题,研究者们提出了很多简化模型,其中最著名的是BGK 模型。BGK 模型假设碰撞过程会使分布函数f不断向其在平衡态下的分布函数f(eq)靠近,且碰撞引起的分布函数变化量与此状态下分布函数f与平衡态分布函数f(eq)的程度成正比,比例系数为(τ0为弛豫时间),利用该模型可将BTE 方程简化为Boltzmann-BGK 方程(式9),大大降低了数值求解的难度。
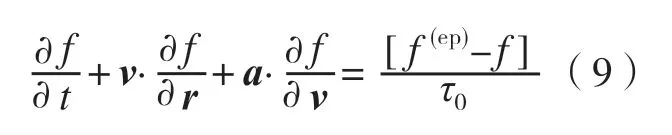
对于导热问题而言,一般可通过求解内能分布函数获得相应问题下的温度场分布和热流密度,进而实现对整体导热问题的求解。相比于宏观热扩散方程,BTE 方程的成立不需要连续性假设和局部热平衡假设。除此之外,相应的内能分布函数微分方程可通过一些操作恢复到宏观导热方程,即该方法也能够用于求解宏观导热问题。因此BTE 方程具有能够准确求解介观尺度以下导热问题和能够同时适用于宏观问题的巨大优势。
对于涉及微观尺度的导热问题,还可以通过求解声子分布函数的BTE方程来对温度场分布和热流密度进行求解。声子分布函数的BTE 方程称为声子玻尔兹曼输运方程(PBTE)。在一些简化假设的基础上,PBTE 方程的形式可以简化为[18]
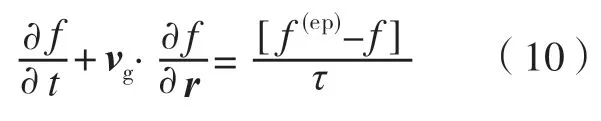
其中,f为声子分布函数;vg为声子群速度;τ为声子碰撞弛豫时间;f(ep)是声子平衡态分布函数,满足Bose-Einstein 分布。进而可通过式(11)获得声子能量密度的分布函数e(T):
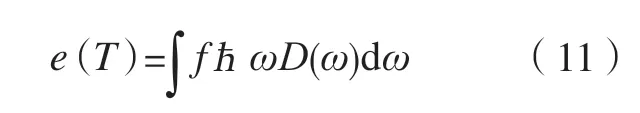
其中,ħ为约化普朗克常数;ω为角频率;D(ω)为声子态密度。
除此之外,还可以直接通过声子分布函数和声子能量密度分布函数间的数学关系构造关于声子能量密度分布函数的BTE 方程式(12),通过直接求解该微分方程获得声子能量密度分布
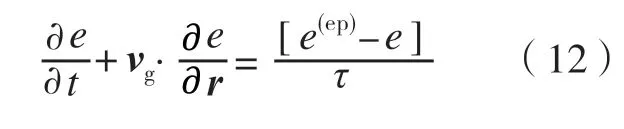
在获得了声子能量密度分布函数后,即可以通过该物理量求解材料内各处的热流密度,从而实现对导热问题的求解。
玻尔兹曼输运方程法是研究微纳米尺度传热问题的一种基本且具有普适性的工具。然而对于PBTE 方程而言,声子输运机理相关理论的准确性会直接影响到PBTE 方程计算结果的可靠性。目前对于声子界面散射等机理尚未建立完善的理论[19]。这些问题有时会导致PBTE 方程的预测结果与实际结果产生一定的偏差。
(2)基于格子-玻尔兹曼法的热障涂层导热研究。
在热障涂层导热特性的研究方面,为了进一步研究微观和介观下微结构对TBCs 导热特性的影响,近年来一些研究者采用数值求解BTE 方程或PBTE 方程的方法来研究相关材料内的微观导热机理[20-22]。在玻尔兹曼输运方程的数值计算方面,一般可直接采用格子-玻尔兹曼法(Lattice boltzmann method, LBM)。格子-玻尔兹曼法是求解BTE 方程相关问题的通用方法,其本质上是Boltzmann-BGK 方程的离散化形式,亦可用于PBTE 方程的数值求解[22]。相比于基于宏观傅里叶导热的数值计算方法,由于格子-波尔兹曼法基于的BTE 方程本身就是可同时适用于宏观介观及微观的理论,因此该数值方法亦具有能够同时适用于宏观介观和微观的优势。这使得该种方法既能够用于传统YSZ TBCs 材料的导热特性研究,也可以用于纳米TBCs 材料的导热特性研究。如对于传统的YSZ 涂层,Wang[20]建立了基于LBM 方法的三维模型,研究并比较了由APS 和EB-PVD 两种方法沉积制备的8YSZ TBCs 中的传热行为,进而详细研究了孔隙度,孔径和孔形等微观结构参数对TBCs有效导热率的影响。Jin 等[21]基于LBM 方法,通过四方结构生成集法(QSGS)和基于YSZ TBCs 真实结构的二进制图像转换法建立了用于预测TBCs 有效导热系数的数值计算模型,并对比了常规YSZ TBCs 和梯度YSZ TBCs 的隔热特性。计算结果发现,虽然两种方法具有不同的机理,但都能够很好地预测TBCs 的有效导热系数,如图1 所示[21-22]。对于纳米热障涂层,金晓强[22]应用LBM 方法从声子玻尔兹曼输运方程出发,研究了纳米结构TBCs 的尺寸效应以及声子界面散射对于导热系数的影响。

图1 基于LBM法对APS TBCs及SPPS TBCs等效导热系数的预测计算Fig.1 Numerical simulation of effective thermal conductivity of APS TBCs and SPPS TBCs based on LBM
(3)基于分子动力学法的理论研究。
除了上文提到的PBTE 方程法以外,分子动力学也是一种可用于研究具有微观特征尺寸的热障涂层材料微观导热机理的数值模拟方法,该方法可通过对分子系统的时间推进进行演化,获得该时间段内相互作用的原子或分子的详细运动情况。相比于PBTE 方程而言,分子动力学法具有在模拟计算时只需要考虑原子间的相互作用,而不需要热输运过程进行假设分析,也无需对声子散射机理有任何了解的优势。分子动力学法具体可分为平衡分子动力学模拟(EMD)和非平衡分子动力学模拟(NEMD)。所谓EMD 法,就是在平衡状态下基于Green-Kubo 线性响应理论得到系统导热系数的方法。其通常是在微正则和正则系综(Microcanonical ensemble/canonical ensemble)下进行的。但对于实际材料而言,当需要考察其热传导体系中存在温度梯度和不可逆热流时,EMD 方法就不再适用,此时需要通过NEMD 法模拟体系中的不可逆非平衡过程。早在2001 年,Patrick 等[23]就用分子动力学法研究过ZrO2和YSZ 材料中的热传输机理。近年来随着计算机性能的提升,分子动力学法得到了更加广泛的应用。
对于热障涂层而言,基于宏观傅里叶导热的数值计算方法无法研究具有微纳结构或涉及到掺杂的新型TBCs 材料的微观导热机理。而分子动力学刚好可以解决上述问题,从微观角度对微结构影响热障涂层导热特性的机理进行研究。因此近年来一些研究者开始逐步基于分子动力学对纳米YSZ 涂层及稀土氧化物掺杂YSZ 涂层的微观导热机理进行数值研究[24-27],如对于YSZ 涂层,Wang 等[24]基于分子动力学(MD)研究了YSZ 材料的热性能,并研究了YSZ 材料中的均方位移(MSD)、状态振动密度(VDOS)和原子运动。模拟结果表明,孔在抑制热传导过程中起着关键作用。Zhao 等[25]利用非平衡分子动力学(NEMD)模拟研究了纳米多孔YSZ 的热导率,模拟基于的4% YSZ 原子结构模型如图2(a)所示[25],并全面地研究了横截面积、孔径、结构长度、孔隙率、Y2O3浓度和温度对热的影响。模拟结果表明,孔隙的存在强化了涂层内部的声子散射,因此使导热系数降低。纳米多孔YSZ 的热导率小于扩散极限,并且随着孔隙率的增加而降低,但是随着孔径的增加而增加,如图2(b)所示。从图2(c)中可直观地看出,NEMD 法对纳米多孔YSZ TBCs 导热系数的预测结果相比于PBTE 而言具有更高的准确度。模拟结果还发现纳米多孔YSZ 的热导率几乎取决于Y2O3的浓度和温度,即非常短的MFP 声子对涂层的热导率起主要作用。然而目前利用分子动力学研究热障涂层材料微观导热机理的研究依然较少,相应的微观导热机理也需要在未来进一步进行深入研究。
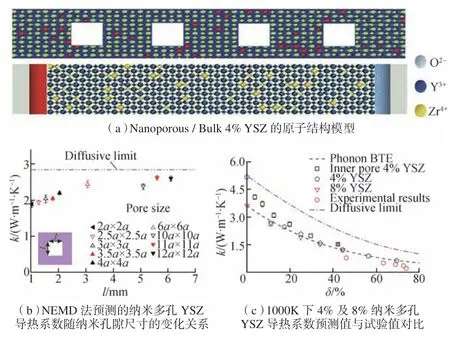
图2 NEMD法对纳米多孔YSZ导热系数的预测Fig.2 Predication of thermal conductivity of nanoporous YSZ based on NEMD
对于稀土氧化物掺杂YSZ 涂层,Wang 等[26]利用分子动力学方法,从声子态密度和点缺陷散射模型出发来研究Sc2O3共掺杂YSZ(ScYSZ)的微观导热机理并解释导热系数的变化。结果表明,与传统的YSZ 相比,ScYSZ 具有较低的声子基团速度和热导率。而由于温度、结构密度、晶格缺陷和化学成分的综合作用,ScYSZ 的热膨胀系数又与YSZ 相当。这些都说明ScYSZ是一种具有良好热物理特性的潜在TBCs 候选材料。赵梦甜[27]基于分子动力学法构造了 YSZ 和 ScYSZ 的晶体结构模型,研究了不同温度、掺杂浓度和纳米孔对 YSZ 和 ScYSZ两种热障涂层材料的热导率的影响。
3 热障涂层导热特性的试验研究
在试验方面,相关文献一般集中于通过简单测量热障涂层结构的等效导热系数,并根据不同热障涂层的特征尺度,结合不同的物理模型以分析微观结构、烧结温度、材料成分、制备方法等因素对热障涂层导热性能的影响以研究YSZ 的导热特性和隔热性能[28-53]。
目前热障涂层的试验大部分基于最常用的YSZ 材料[29-39]:Hu 等[29]基于叔丁醇(TBA)的凝胶浇铸工艺制造了多孔8YSZ 陶瓷,并在室温下试验测量了多孔YSZ 的导热系数。结果表明YSZ 的高孔隙率及均匀多孔结构阻碍了热传导过程,从而导致多孔YSZ 的超低热导率,且试验热导率与从EMT 方程式推导出的理论值非常吻合,试验测量了从室温到1400℃条件下多孔8YSZ 陶瓷的热扩散率、比热容及导热系数变 化[30]。结果表明,随着测量温度的升高,8YSZ 多孔陶瓷的热扩散率在一定范围内先降低后升高;多孔8YSZ陶瓷的导热系数则随烧结温度的升高而升高。梁波等[31]利用APS 技术和纳米粉体造粒料制备了摩尔分数3%的YSZ 热障涂层,采用差示扫描量热仪(DSC)和激光脉冲法热导仪对涂层的热物性进行了试验研究和理论分析。试验发现结构中大量垂直热流方向的微细裂纹和均匀小气孔对声子起到了很强的散射作用, 从而使涂层具有很小的导热系数(0.63~0.80W/(m·K))。因此,晶粒长大、气孔率降低这些因素可导致涂层的导热系数升高, 降低涂层的隔热性能。Jang 等[32]应用脉冲热成像法测量了EB-PVD ZrO2–Y2O3热障涂层的导热系数,试验结果发现涂层的导热系数及比热容均会随着Y2O3的成分数量增加而下降。Ghasemi 等[33]通过APS 制备了由YSZ 陶瓷外涂层和NiCrAlY 金属结合涂层组成的纳米结构TBCs,并用Nd:YAG 脉冲激光对表面层进行处理。试验研究了表面激光处理对TBCs 表面层微结构的影响。试验结果表明,纳米结构的等离子体喷涂涂层包含未熔融或部分熔融的纳米颗粒和柱状晶粒,而激光处理后的涂层微观结构则由断裂表面的柱状晶粒和表面的等轴晶粒组成。激光上釉有助于消除通过等离子喷涂方法沉积的涂层的表面孔隙和其他结构缺陷,有助于改善其表面质量;但涂层的隔热性能会由于表面微结构的改变而略微降低。Ghasemi 等[34]还研究了纳米结构的YSZ 热障涂层的粘合强度和隔热性能,并将其与常规YSZ TBCs 进行了比较。结果发现,与传统的TBCs 相比,纳米YSZ 涂层内部存在大量孔隙,且Splat 边界(Splat boundaries)增加,这两种因素导致散射声子增强,从而导致纳米结构的YSZ 热障涂层具有更低的导热系数即更强的隔热能力。钟颖虹等[35]采用超音速火焰喷涂黏结层、APS 陶瓷层制备了双层结构的TBCs,通过激光脉冲法试验测量了涂层的导热系数,并对涂层的隔热性能进行试验研究。结果发现陶瓷涂层的热导率随温度的升高而减小,大致在800℃最低;此后,由于高温辐射传热效应逐渐增强,热导率逐渐缓慢增大。在1100℃下热导率为0.99W/(m·K),隔热效果可达到155℃。Jiang[36]利用试验研究了由溶胶-喷涂热解粉等离子喷涂的纳米结构4YSZ 涂层的相稳定性和导热性,结果发现,由于纳米晶粒和孔隙产生的晶界上的界面无序声子散射,4YSZ 涂层具有很低的导热系数(0.8~1.2W/(m·K)),且几乎不随温度变化。Torkashvand[37]通过试验和模拟相结合的方式研究了孔隙率的大小,孔隙的分布以及热处理方式对APS TBCs 的导热系数的影响。结果发现,在没有改变孔隙的方向及分布的情况下,孔隙率大小对导热系数的大小有很大的影响,在改变孔隙方向时上述关系依然保持。且当孔隙率很大时,相比而言孔的分布情况和方向对导热系数的影响就显得微不足道。试验结果还发现,1070℃时的热处理会使TBCs 的导热系数增加5%~30%,且孔隙率越大,烧结过程对TBCs 导热系数大小的影响越明显。Zhao[38]通过悬浮液等离子体喷涂(SPS)制造了YSZ 涂层,并用激光闪射法测量了YSZ 涂层的导热系数以研究孔隙率对涂层导热系数的影响。试验发现,增加总孔隙率能够有效地降低SPS YSZ 涂层的导热系数;且相比于较大的孔隙而言,热性能对纳米/亚微孔隙产生影响的敏感度更高。因此增加纳米亚微孔的含量能够有效地增益SPS YSZ 涂层的隔热性能。Zhou[39]通过APS 法在覆涂K417G 高温合金的NiCoCrAlYCe 上加工纳米t′-8YSZ涂层,并比较了其与常规t′-8YSZ 涂层的热物理特性。试验结果表明,纳米t′-8YSZ 涂层比常规的t′-8YSZ涂层具有更低的导热系数,尤其是在1000℃以上时。因此纳米t′-8YSZ 也具有更强的隔热能力。
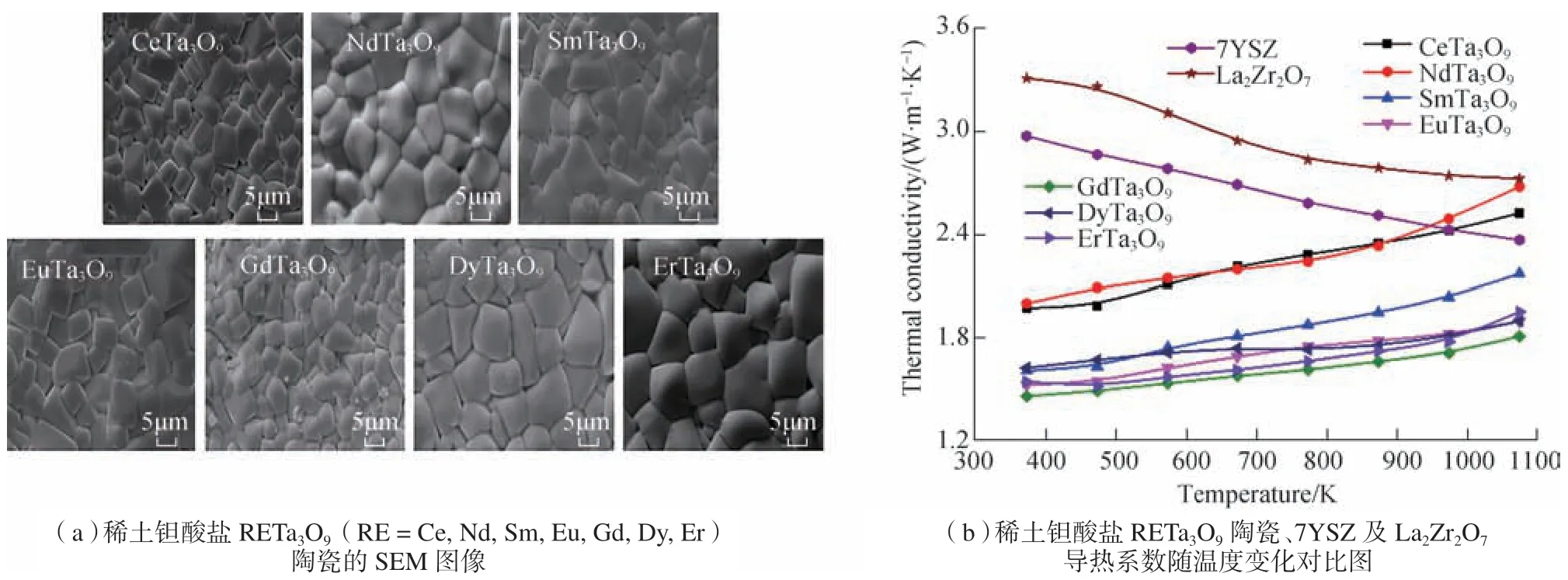
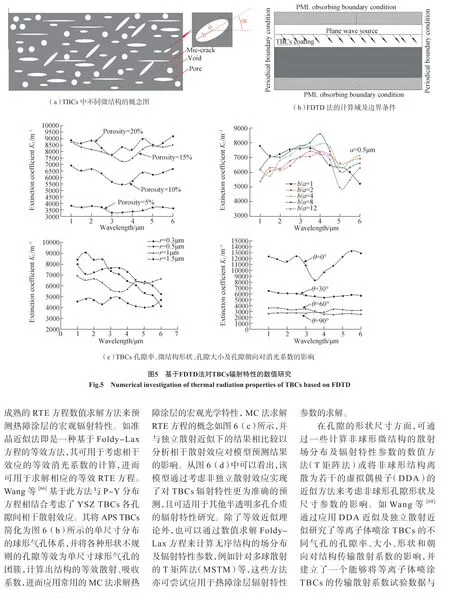
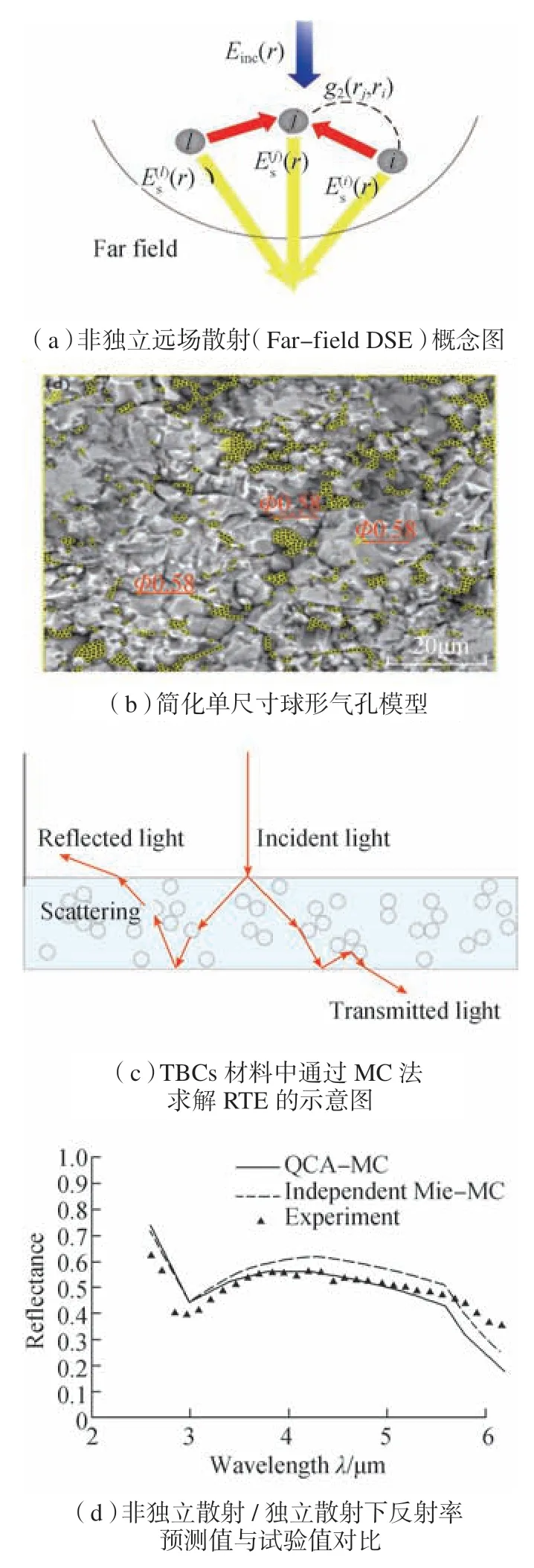
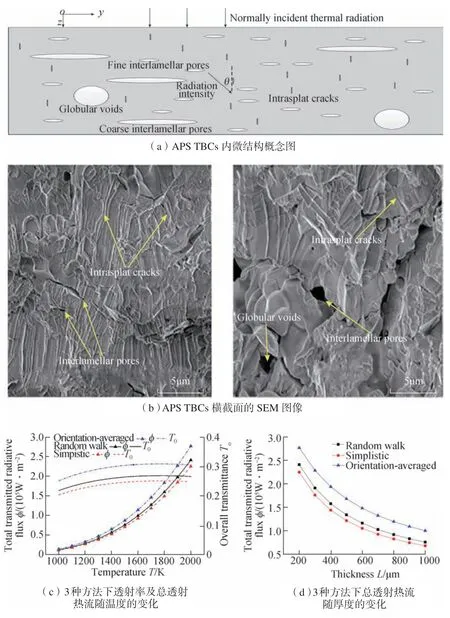
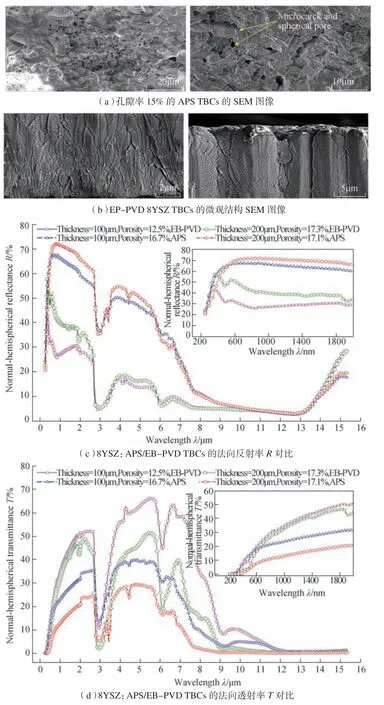
近年来,随着热障涂层材料的不断发展,围绕着新型TBCs 材料的导热特性及相关机理的研究也在逐步增多。目前有两大类主要热障涂层新型材料,分别为稀土氧化物掺杂YSZ 和锆酸盐材料。针对稀土氧化物掺杂的YSZ 涂层,Liu[40]试验测量了掺La2O3的YSZ 材料的相稳定性和导热系数,试验发现La2O3的掺杂可有效地降低YSZ 材料的导热系数。Liu 等[41]试验测量了ScYSZ 在30~700℃范围内的导热系数,结果发现,由于Sc2O3的引入YSZ 材料内会存在更多的空位和替代缺陷,使得ScYSZ 比YSZ 材料具有更低的导热系数和热扩散率。Yang 等[42]用激光闪射法测量了室温到800℃范围内[(ZrO2)1−x(CeO2)x]0.92(Y2O3)0.08(0 图3 稀土氧化物SnO2掺杂YSZ的导热试验研究Fig.3 Experiment of thermal conduction properties of SnO2 doped YSZ 针对锆酸盐热障涂层材料,Xiang[47]利用激光闪射法测量了La2(Zr0.7Ce0.3)2O7热障涂层(LZ7C3)的导热系数,试验结果发现,LZ7C3的导热系数随着温度的升高而逐渐降低,直到1200℃,其导热系数仍在0.79~1.02W/(m·K)范围内,相比纯La2Zr2O7的导热系数降低了近50%,因此是一种非常有前景的热障涂层材料。Zhang[48]制备了掺有Ca 和Mg 的La2Ce2O7,并用激光闪射法测量了等效导热系数。结果发现掺杂锆酸盐材料的导热系数要低于普通的锆酸盐材料,这可以归因于晶格中空位引起的声子散射。Yang[49]研究了La2(Zr0.75Ce0.25)2O7(LCZ)详细的结构演变过程,并通过激光闪射法测量了材料的导热系数,结果发现,LCZ 陶瓷具有极低的导热率(0.65W/(m·K),1200℃),约为YSZ 材料的1/3。Zhang[50]制备了La2Zr2O7@YSZ 核壳结构复合陶瓷,以解决锆酸盐材料断裂韧性较低的缺陷。该试验采用激光闪射法、高温膨胀计和纳米硬度测试分别研究了La2Zr2O7@YSZ 复合陶瓷的导热系数、热膨胀系数(CTE)和机械性能。结果发现,在导热系数方面,复合结构的导热系数在200~1000 ℃为1.7745~2.3076 W/(m·K),介于La2Zr2O7和YSZ两种材料之间,且随着温度的升高,复合结构的导热系数逐渐接近于YSZ 材料。 除了上述两种新型材料外,近几年来,随着材料加工技术的发展,更多其他掺杂材料、新型加工方法以及新型微观结构都被用于提升热障涂层的综合性能。其相关的导热特性及隔热性能亦被试验研究。Chen 等[51]开发了基于稀土钽酸盐RETa3O9(RE = Ce, Nd, Sm, Eu, Gd, Dy, Er)的陶瓷涂层,其微观结构的SEM 图像如图4(a)所示。结果发现,在373~1073K 范围内,钽酸盐陶瓷涂层导热系数为1.33~2.37 W/(m·K)。如图4(b)所示,相比于7YSZ[18]和La2Zr2O7[19]两种热障涂层材料,稀土钽酸盐陶瓷具有更低的导热系数。因此其有望成为新一代的TBCs 材料。Kulczyk-Malecka[52]采用激光闪射法测量了从室温到1000℃范围内由SPS 法制备的内含10%或20% MoSi2(用于延长TBCs使用寿命)的YSZ 热障涂层的导热系数,进而将测量结果与基于微结构的有限元模型和非对称Bruggeman模型、Nielsen 模型等分析模型的计算结果进行比较,以研究添加MoSi2颗粒以及内部微孔结构对导热系数的影响。结果发现,TBCs 的热导率随MoSi2体积分数的增加而出现很大的非线性增加,且与MoSi2颗粒的长径比有关。Arai[53]应用ZrO2和聚酯的粉末混合物,试验制备了具有由大开孔分布组成的微结构的多孔YSZ TBCs(P-TBCs)用以研究多孔TBCs 结构中的孔隙对其导热性能的影响,并基于SEM 扫描图像采用有限元法对结构中的传热过程进行分析。试验结果表明,P-TBCs 的导热系数随着孔隙率的增加而单调下降;此种大孔隙开口结构的引入可以使TBCs 的导热系数低至0.3W/(m·K),且可以通过调节粉末混合物中的聚酯含量来调控多孔TBCs 的导热系数。模拟结果表明,P-TBCs 内存在开孔增加了热流线的长度,因此具有更低的导热系数。上述的研究都为未来发展具有更高性能的热障涂层材料打下了坚实的基础。 图4 钽酸盐陶瓷的相关试验研究Fig.4 Experiment of thermal conduction properties of tantalate TBCs 由于热障涂层的工作温度在1000℃以上,因此热辐射传热会对热障涂层的隔热性能造成很大程度上的影响。目前,对热障涂层内部热辐射的理论和试验研究主要针对YSZ TBCs。由于YSZ 陶瓷材料的可见光及红外波段(0.3~8μm)热辐射特性呈现出半透明性质,因此在高温运行条件下YSZ 材料的热辐射传递必将对热障涂层的隔热性能产生明显影响。 在热障涂层热辐射特性的理论研究方面,早期研究通常基于宏观等效导热系数法对TBCs 的热辐射传热等效微导热的一部分来进行研究。然而这些宏观等效导热模型普遍存在前置适用条件,且无法对相应的微观辐射机理进行研究。目前,多数研究通过辐射传输理论及电磁学分析理论相结合的方式研究TBCs 内的热辐射传热特性。 1.1 宏观等效导热系数法 在理论方面,早期的研究通常将TBCs 的热辐射传热等效为TBCs 导热的一部分,通过建立等效导热系数模型的方法计算TBCs 辐射特性对整体隔热特性的影响。其中比较常用的是Rossland 扩散近似等效导热模型。Rossland 模型是一种计算多孔介质辐射特性的常用模型,其是一种研究材料热辐射特性的宏观方法。热辐射传热的等效导热系数可以由式(13)进行定量计算: 其中,σ为Stefan-Boltzmann 常数;T为热障涂层温度;n为折射率;KR为Rossland 平均消光系数。在热障涂层辐射特性的早期研究中,该模型得到了大量的应用。Golosonoy[12]采用过Rossland 扩散近似模型来计算热障涂层中的辐射热流以及辐射热流占总体传热量的比重。然而这些等效计算模型的使用多数是有前置条件的,Rossland 近似模型只能在材料为强吸收或弱吸收的前置条件下才能有效计算[6]。因此采用等效导热系数法预测涂层的辐射特性将会存在较大的误差,且也无法用其研究TBCs 的微观辐射机理。 1.2 辐射传输理论及电磁学分析理论 为了解决上述问题,更深入地研究热障涂层微观机理,近10 年来不少研究者将目光聚焦到了热障涂层微观辐射特性参数的精确计算及微观结构对其辐射特性影响的研究上。 热障涂层内的辐射传输问题可以归类为多孔介质的辐射传输问题。目前,热障涂层这类多孔介质中的辐射特性可以利用两大类理论进行研究,一类为辐射传递理论,其采用经典的辐射传递方程(RTE)来描述光强在无序介质内的传输特性;另一类为电磁波分析理论,其通过求解Maxwell 方程来获取无序介质中的电磁场分布,从而获得辐射特性参数,进而求解出介质中的辐射传递过程。上述两种方法虽然是通过不同途径推导获得的,但实质上只是从两个不同的角度描述了辐射传输问题,且目前已证实RTE 方程可由Maxwell 方程推导获得,因此两种方法并不存在矛盾。 第1 类方法是传统的辐射传输理论,辐射传输理论是基于辐射传递方程(RTE)计算介质辐射特性的一种理论。一般而言,热障涂层这类无序介质的辐射特性主要通过数值求解标量RTE 方程获得,标量RTE 方程的形式可以表示为: 其中,I为光谱辐射强度;Ib为黑体光谱辐射强度;κs为散射系数,κa为吸收系数,二者之和为消光系数κe(κe=κa+κs);P(Ω',Ω)为散射相函数。该方程可良好地应用于干涉效应微弱的宏观、介观物体的热辐射特性计算。 在热障涂层辐射特性的研究方面,早期文献一般直接采用该方法来研究热障涂层内的辐射特性。如Dombrovsky 等[54~56]根据传输理论推导出了多孔介质中的RTE 方程,该方法被称为修正的二流法,能够考虑多孔介质中的各向异性。目前该方法仍是辐射传输反问题求解的主要理论模型之一。在数值计算方面,王平阳等[57]采用光线踪迹/节点分析法求解RTE 方程以计算各向同性散射性介质内的辐射传递系数。结合控制容积法研究了热障涂层内的辐射与导热瞬态耦合换热,还采用基于光线踪迹/节点分析法对吸收、各向同性散射非灰体涂层内的辐射与导热瞬态耦合换热进行数值模拟[58]。随着热障涂层材料的发展,为了更好地研究涂层中微纳结构对辐射特性的影响,研究者们通常结合相应的电磁学理论求解涂层的辐射特性参数,并在一定假设条件下应用RTE 方程或等效RTE 方程求解热障涂层的宏观辐射特性。 第2 类方法是电磁波分析理论,该方法基于Maxwell 方程对介质中的辐射特性进行计算分析。由于Maxwell 方程在热障涂层微纳结构的特征尺度上总是成立的,且基于求解Maxwell 方程的电磁波分析理论可以更加清晰地分析研究热障涂层材料的微观结构参数对其辐射特性的影响机理,因此近年来为了建立更具有普遍性的计算模型,并将热障涂层的微观结构性质考虑在计算模型之中,一些研究从电磁波分析理论的角度出发建立能表征热障涂层微观结构的理论计算模型以研究热障涂层的辐射传输特性。 最初被选用计算热障涂层辐射特性参数的电磁波分析理论是Mie理论。早在1908 年,Mie[59]就基于 Maxwell 方程求解出单色平面波球体散射场的严格解析解。由于Mie理论的相关公式形式较为简单且计算快捷,且在独立散射近似的条件下,RTE 方程仍然成立,相应的较为成熟的数值计算方法仍可继续应用,因此早期的研究者们常将热障涂层的微观气孔结构形状简化为球形,在此基础上基于独立散射近似和Mie理论模型来求解热障涂层的散射系数和吸收系数。如Dombrovsky 等[60]基于Mie 理论计算孔隙率较低的陶瓷材料的散射系数,计算结果与试验结果能够较好地符合。由于Mie理论模型中涉及到球体直径d这一几何参数,因此可应用Mie 理论对气孔的大小及分布情况对热障涂层辐射特性的影响进行定量分析。Yang 等[61]基 于Mie 理 论 初 步 研究TBCs 微结构对其散射特性的影响,结果发现,对于孔隙率为5%的8YSZ 涂层,Mie 理论的散射系数计算结果能够与试验结果较好符合,且孔隙的大小和分布直接影响到散射系数的大小。 然而,实际热障涂层中的微观孔隙形状是十分复杂的,如在APS TBCs 中存在沿水平方向的椭球气孔以及微裂纹,EB-PVD TBCs 中则存在着大量沿竖直方向的柱间间隙和羽毛状条纹,这些结构都不是球体,也不能简化为球体,且能够应用独立散射近似假设求解辐射特性参数的孔隙率上限一般为5%,而常用的传统YSZ 热障涂层的孔隙率基本在15%左右,这表示独立散射近似在多孔热障涂层中是不成立的,随着孔隙率变大带来的相干散射效应会对辐射特性参数的计算造成很大的影响。上述的两个因素都会直接导致用Mie 理论预测的辐射特性参数与实际测得的辐射特性参数产生较大偏差。为了通过数值计算准确预测热障涂层的辐射特性参数,并研究微观结构对其辐射特性的影响,必须考虑气孔的实际形状和气孔之间的相干散射效应。 在介观和微观尺度,可以通过直接数值求解Maxwell 方程的方法将上述两种因素考虑在内:时域有限差分法(FDTD)是一种可在微观和介观尺度直接求解Maxwell 方程的数值方法,该方法通过在Yee 单元空间中离散Maxwell 方程对结构中的场分布进行自行精确求解[62]。相比于其他辐射特性理论计算模型,FDTD 法有不需要人为的考虑微结构的形状尺寸和微结构间的相干效应、各向异性等因素对模型准确性的影响,操作较为简便的优势。因此对于热障涂层这种具有复杂内部结构的多孔材料而言,FDTD 法是一种研究其辐射特性的比较合适方法,该方法能够准确求解其辐射特性参数,且能够用于研究其微观结构参数对整体辐射特性的影响。Zhang 等[63]利用FDTD 法比较全面地研究了TBCs的孔隙率,微结构的大小、形状、朝向对TBCs 辐射特性的影响。TBCs 中的微结构可简化为如图5(a)所示的概念图,FDTD 模拟的计算域及边界条件如图5(b)所示,计算结果发现,如图5(c)所示,在孔隙率方面,孔隙率越大则消光系数越大,越有利于TBCs 隔热。在孔隙大小和形状方面,孔隙越小消光系数越大,而孔隙的形状对消光系数的影响则可以忽略不计。在朝向方面,随着孔隙方向从水平到垂直的变化,消光系数大幅下降,隔热特性削弱。Yang 等[64]也基于FDTD 法与试验测量相结合研究了EB-PVD TBCs 的红外辐射特性,并详细探讨了涂层内部的红外辐射传输机理。试验结果表明,EBPVD 本身具有的柱间间隙、羽毛状条纹和闭合的球形毛孔等微观结构均对其辐射特性有一定的影响,尤其是封闭孔隙率对宏观辐射特性具有重大影响。由于闭孔的散射,孔隙率越大越有利于增加TBCs 对红外光的反射。因此在实际工程之中,可以通过优化闭孔孔隙率这些微结构参数来降低辐射热通量,以优化EBPVD TBCs 的隔热性能。Shi 等[65]基于FDTD 法,研究了由QSGS 算法生成的APS 层状微观结构对8YSZ TBCs 辐射性能的影响。孔隙率对涂层的辐射特性有很大的影响,孔隙率越大,TBCs 的散射系数和反射率越大,越利于隔热。孔隙率为20%将是协调隔热效果与制造工艺之间的良好折衷。当孔隙率固定时,平均孔径大小对TBCs 的散射系数有显著影响,而对吸收系数的影响则微不足道。计算模型还确定了在等离子喷涂的8YSZ TBCs 中的最佳微观结构,可使在1400~2000K 的温度范围内,黑体辐射的总反射率到达82%以上。上述结果直观地展现了热障涂层微结构对其辐射特性的影响,对热障涂层的设计和制造有一定的指导意义。 然而由于FDTD 是对Maxwell方程做精确数值求解,而热障涂层的实际微结构又十分复杂,因此如用FDTD 法求解实际热障涂层的辐射特性必然面临着运算量大、运算时间长的问题。这导致该种方法很难真正运用到实际的工程应用中,且通过FDTD 也并不能揭示微结构对辐射特性产生影响的机理。因此为了解决YSZ TBCs 辐射计算模型不考虑微结构间相干散射效应及微结构各向异性特征影响的不足之处,需要应用考虑了上述因素的电磁学理论构建预测结果更为精确的理论计算模型。 在相干散射方面,图6[66-67](a)给出了散射体的非独立远场散射(Far-field dependent scattering effects)概念图,当散射体间距达到与波长相当的量级时(即无法满足k(δ-2a)>>1,其中k为波矢,a为两散射体间距),散射波会产生干涉效应,这种非独立远场散射即为相干散射。当考虑相干散射效应时,传统的RTE 方程会存在失效的问题。实际上,RTE 方程是Bethe-Salpeter 方程在忽略一切干涉问题下的简化结果,因此当微结构间存在相干散射时,应该通过求解Bethe-Salpeter 方程或Foldy-Lax 方程来求解其场分布及辐射特性参数,但出于实用性考虑,实际上仍可以通过一些等效近似理论使RTE 方程的形式得以保留,计算出考虑相干散射因素的修正的辐射特性参数,进而依然通过目前较为 图6 相干散射模型 Fig.6 Dependent scattering effects model TBCs 的微观结构联系起来的逆相关模型,拟合结果能够与试验良好吻合。最后利用该逆相关模型计算了不同工作温度下的最优化微观结构。该文充分地定量研究了等离子体喷涂TBCs 微观结构对TBCs 辐射特性的影响,其建立的逆相关模型为热障涂层的实际设计提供了极好的指导。 除了相干散射效应和微结构的几何参数外,热障涂层辐射特性的各向异性建模一直是热障涂层理论计算模型中的一个空白。为了填补这一研究空白,完善TBCs 辐射特性的理论计算模型,Wang 等[69]首次研究了APS TBCs 辐射特性的各向异性,通过应用DDA 求解Maxwell 方程的方式获得散射系数、散射平均自由程、不对称因子等微观各向异性辐射特性参数,进而通过随机游走法求解各向异性介质中的宏观传输平均自由程,最后结合扩散通量近似定量计算各向异性对APS TBCs 的宏观辐射特性的影响并与传统的简易(Simplistic)方法及常用的方向平均法(Orientation-average)的计算结果进行对比,结果如图7 所示[68]。文献结果显示辐射各向异性对宏观辐射特性的影响随工作温度升高而增大。论文首次研究了APS TBCs 辐射特性的各向异性,文中的数值计算方法对进一步研究热障涂层材料中各向异性对结构总传热特性的影响有重大意义,并为研究其他各向异性多孔介质的辐射特性打下了良好的基础。 图7 考虑各向异性的散射模型Fig.7 Scattering model considering anisotropy effect 在试验方面,大部分研究集中于通过试验测得热障涂层的宏观辐射特性,之后应用四流法、修正的二流法等模型结合试验数据计算出TBCs的辐射特性参数[61,70-78]。目前大多数试验一般基于传统的YSZ TBCs材料[61,70-72],如Dombrovsky 等[70]试验测量了孔隙率为16%的多孔氧化锆陶瓷在2.5~9μm 红外波段的反射率和透射率,并通过试验数据结合修正的二流法精确计算了多孔结构的散射系数和吸收系数。Stuke 等[71]试验测量了多孔YSZ 在0.3~2.5μm波段的反射率和透射率,并结合修正的二流法计算出辐射特性参数,用以研究孔隙率对散射系数的影响。Yang 等[61]通过试验测量了APS 热障涂层在200nm~15μm内的法向半球反射透射光谱,进而通过四流法获得了结构的散射系数和吸收系数。并用Mie 理论初步研究了TBCs 微结构对其散射特性的影响,其工作将热障涂层在短波段的试验数据扩展到一个新的极限至250nm,丰富了热障涂层的图谱数据。Yang等[72]还通过试验结合四流法首次比较了250nm~15μm 波段EB-PVD 和 APS两种TBCs 的辐射特性参数,并研究了两种结构孔隙特征和晶格排布对TBCs 内容积散射的影响。试验结果表明(图8)[72],相比于EB-PVD 而言APS 具有更高的反射率。这主要是由于APS 的水平晶格排布会对准直入射光产生后向散射效应,因此增大了反射率;且具有水平孔隙及晶界的APS TBCs 的孔隙率增加会对其反射率有增益效果。进而随着TBCs 材料的不断发展,近期的试验已不再局限于传统的YSZ 材料,如Wang[73]在0.8~15.0μm的波长范围内测量了不同厚度的Free-Standing等离子喷涂BaZrO3TBCs 的室温方向半球反射率和透射光谱,并基于试验测量结果通过四流法获得了吸收系数和散射系数。结果表明,在6μm以下时,BaZrO3呈现高散射、低吸收特性。随后BaZrO3的吸收系数在波长为6μm 处开始迅速增加,在7μm 处出现明显的吸收峰,而散射系数随波长的增加而减小,接着其[74]又在0.8~6.0µm 的波长范围内测量了不同厚度的Free-standing 等离子体喷涂SrZrO3涂层的室温方向半球反射率和透射光谱,研究了吸收系数和散射系数与波长的关系,并与传统的YSZ TBCs 进行对比。结果发现,在测得的波长范围内,SrZrO3的散射系数高于YSZ 的散射系数,是一种很适合用于TBCs 的材料。其吸收系数极低,且散射系数随着波长的增加而减小。 图8 APS TBCs/EB-PVD TBCs辐射特性对比Fig.8 Comparison of thermal radiation properties of APS TBCs and EB-PVD TBCs 除此之外,一些新型结构的TBCs 材料的辐射特性也已被试验研究,如对于在梯度热障涂层,Ge[75]通过APS 法制备了30 多种具有不同的多层结构、孔隙率和厚度的YSZ/ NiCoCrAlY 双相TBCs 和多层FGTBCs 样品,通过紫外-可见光谱仪和FTIR 测量了0.3~15μm 波段的反射率和透射率光谱。根据试验测量结果,通过四流法获得了结构的辐射特性参数。结果表明,与传统的YSZ TBCs 相比,功能梯度材料(FGM)具有更大的吸收系数和更小的散射系数,这使得FGM TBCs 的隔热性能弱于传统 YSZ TBCs。紧接着,Ge[76]建立了基于二流法和多谱带法的辐射传热模型,通过该模型计算了FGTBCs 内部的稳态温度分布和稳态热通量,并将计算出的温度分布与仅考虑热传导的计算结果进行对比。结果表明,当包含更多的梯度层时,隔热性能变差。为解决FGM TBCs隔热性能较传统TBCs 低的问题,可以通过扩大YSZ 顶层的厚度比或通过优化结构设计来改善FGTBCs 的隔热性能。这些都为FGM TBCs 的设计提供了一定的指导。对于一些具有特殊微观结构的新型TBCs 材料,如光子玻璃,Shang[77]制备了一种基于YSZ 微粒无序排列生成的高温稳定光子玻璃结构(YSZ-PhG),其具有低热导率并能抑制外部辐射热传递,试验表明,由于相邻YSZ 微粒点接触的存在,YSZ-PhG 具有极低的导热系数(0.03W/(m·K)),且在1400℃下退火5h 后,结构的导热系数仍远低于常规的YSZ 热障涂层。同时该结构还能够对1~6μm 的光产生强散射,试验测得100μm 厚的结构可具有84%的反射率,在1400℃下,辐射等效导热率为0.2W/(m·K)。 然而上述的试验测量均是在常温下进行的,并没有考虑温度对TBCs 辐射传输的影响。近年来,温度对热障涂层热辐射特性的影响也逐步被考虑。Zhao[78]用两基板法测量了850~1150℃高温下APS 8YSZ涂层在1.4~2.4μm 波段的反射率和透射率,并通过四流法计算了8YSZ TBCs 的散射系数和吸收系数。结果表明,反射率随波长和温度的升高而降低,透射率则随温度的升高而升高,且散射系数随波长增大而减小,而对温度的依赖性较小。吸收系数则随温度的升高而增加,对波长变化的依赖较小。由于吸收系数很低,因此8YSZ TBCs 可以视为纯散射涂层,应用零吸收二流法模型也可准确预测TBCs 的辐射特性。 目前相比于导热特性研究而言,对热障涂层辐射特性的研究相对较少,且研究对象大部分集中于常用的YSZ TBCs 材料。一些新型的TBCs材料如掺杂YSZ、锆酸盐材料及具有新型结构的YSZ 材料的辐射特性几乎没有相关研究。随着燃气轮机工况温度的不断提高,对新型TBCs 材料的需求在不断增加, 因此相应的辐射特性也需要在未来进一步进行深入研究。 隔热性能是热障涂层最重要的性能指标之一,而在高温工作条件下,导热和热辐射均会显著影响热障涂层的隔热性能。本文综述了近10年内国内外关于热障涂层导热特性及热辐射特性的相关研究,得到了以下结论。在热障涂层的导热特性研究方面: (1)目前大多数研究集中于导热系数的试验测量,其中绝大多数试验基于传统的YSZ 材料、稀土氧化物掺杂YSZ、锆酸盐材料及一些新型TBCs 材料的导热特性也逐步被试验研究。 (2)在理论方面,目前多数研究通过基于宏观热扩散方程的有限元法模拟分析热障涂层内的导热过程。然而随着热障涂层材料的发展,其特征尺寸的尺度不断缩小,在这些尺度下宏观热扩散定律会存在失效问题。因此相关理论研究逐渐呈现了从基于宏观导热向基于介观微观导热的发展趋势。目前,已有不少相关理论研究采用基于BTE 方程的格子-玻尔兹曼法或微观的分子动力学法对纳米热障涂层或稀土氧化物掺杂热障涂层这类具有介观或微观特征尺寸的TBCs 材料进行研究。 相比于导热特性的研究而言,热障涂层辐射特性的研究目前还处在起步阶段: (1)在理论方面,目前的研究通常基于电磁波分析理论和辐射传输理论相结合的方式对热障涂层的辐射传输进行建模计算,最初的研究普遍采用Mie 理论与RTE 方程相结合的方式研究热障涂层的辐射特性,但由于未考虑相干效应和孔隙形状而不能预测出准确的结果。随着孔隙形状,相干散射效应及各向异性等因素的逐步考虑,热障涂层辐射传输的理论模型在相关的电磁波分析理论下变得更加完善。除此之外,还有很多研究直接通过基于求解Maxwell方程的FDTD 法研究热障涂层的辐射特性,但其计算量大,计算时间长的缺点导致该种方法很难真正运用到实际的工程应用中。 (2)在试验方面,大部分研究集中于通过试验测得热障涂层的宏观辐射特性,之后应用四流法,修正的二流法等模型结合试验数据计算出TBCs 的辐射特性参数。随着热障涂层材料的发展,不少新型TBCs 材料的辐射特性也被试验研究。除此之外,温度对热障涂层热辐射特性的影响也逐步被试验研究。 随着燃气轮机工作工况温度需求的不断提升,热障涂层将会不断向具有更小尺度特征尺寸的方向发展,且辐射传热对热障涂层的隔热性能影响也将会随温度逐步增加。因此热障涂层介观尺度以下的导热特性及微观导热机理和一些新型TBCs 材料的辐射理论模型建立问题需要在未来进一步进行深入研究。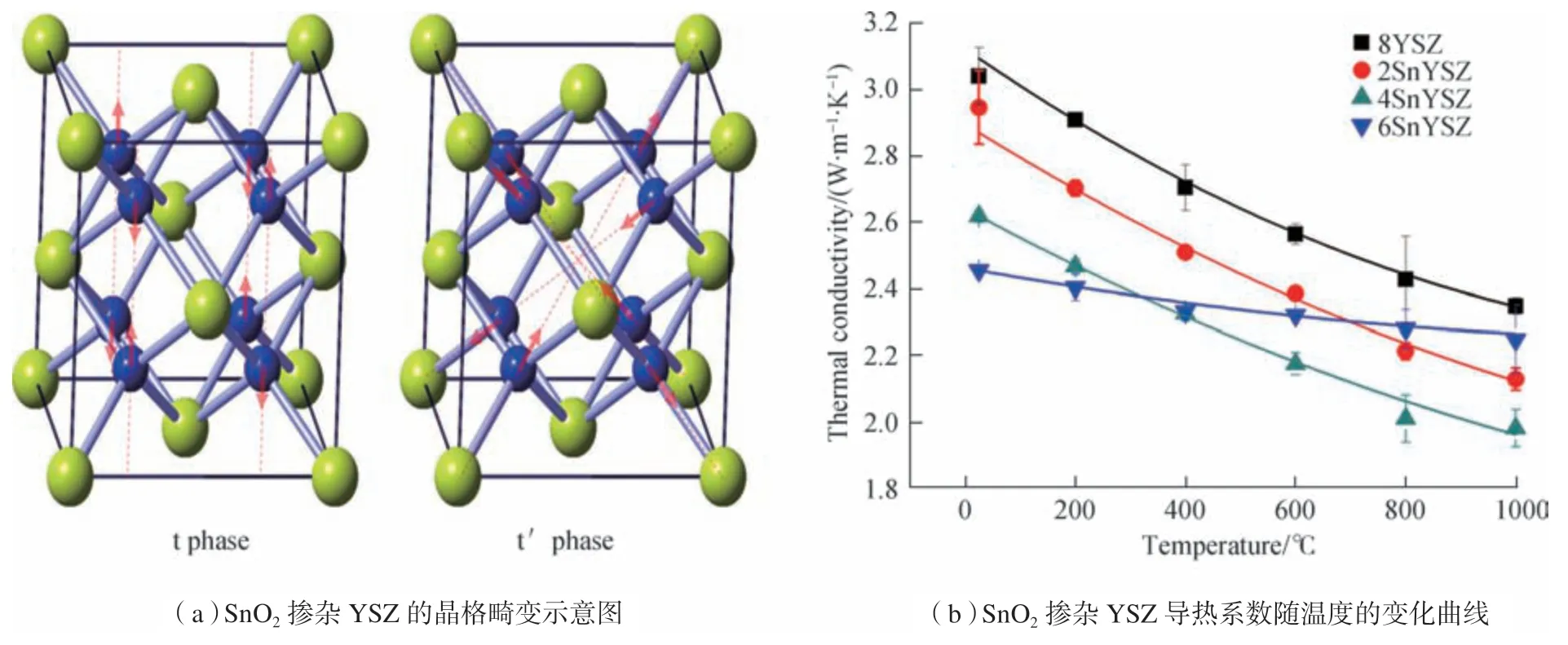
热障涂层的热辐射特性研究
1 热障涂层热辐射特性的理论研究
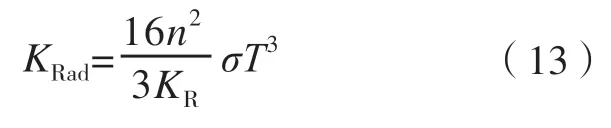
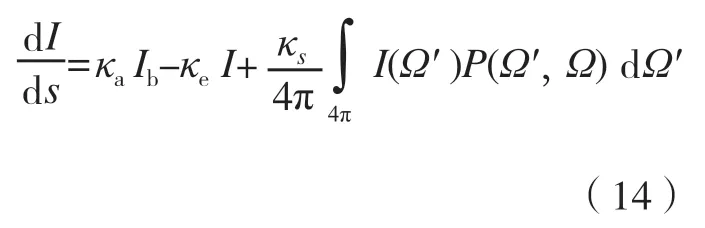
2 热障涂层辐射特性的试验研究
结论

