基于液滴局部轮廓的接触角测量方法

李 健, 费 潇，王腊梅, 赵 珂，金卫凤

(1.江苏大学材料科学与工程学院，镇江 212013；2.江苏大学智能柔性机械电子研究院，镇江 212013; 3.江苏大学机械工程学院，镇江 212013)

液滴在表面上的接触角是表征表面润湿性能的重要参数。一般情况下，表面润湿性能研究需要借助于专用的接触角测量设备，较高的设备投资费用制约相关的研究工作。近年来，图像采集设备得到普遍使用，可实现接触角测量，用于表面润湿性能研究。采用普通图像采集设备测量接触角的关键在于如何对获取的液滴图像进行分析计算以确定出正确的接触角。

接触角测量的结果对研究结论的正确性具有决定性作用。对于接触角小于120°的表面，由于液滴在表面的接触角较小，液滴呈球冠状，此时液滴轮廓可假设为圆弧轮廓，液滴的接触角可在测量液滴高度和液滴轮廓与表面间的接触点间距的基础上计算出来，即实现所谓的量高法[1]；基于圆弧液滴轮廓假设，接触角也可通过量角器来测量。然而，对于接触角较大的情况，如水滴在超疏水表面上的情况，接触角测量将面临较大的问题。李健等[2]研究了接触角测量中的量高法的应用范围，发现采用量高法测量出的超疏水表面上液滴的接触角具有较大的误差：在接触角接近180°时，接触角测量偏差可达20°。为了修正量高法引入的接触角偏差，该工作提出了基于查修正曲线图的接触角修正方法。然而，修正接触角偏差一方面需要预先制定误差修正图，另一方面还需要预先确定液滴的体积，这些要求限制了偏差修正方法的应用。在此背景下，探索方便且较为精确的接触角测量方法仍然具有一定研究价值。

理论上，采用模拟方法可拟合出非球状液滴的整体轮廓，进一步基于拟合的轮廓参数可计算出液滴在表面上的接触角。然而，液滴轮廓模拟拟合需要预先确定诸多参数[3-4]，而且主要针对轴对称非球状液滴的接触角测量。因此，这种方法难以用于液滴轮廓参数如液滴体积等参数未知的情况，例如，对缺少液滴图片标尺的文献上的液滴接触角的回溯分析就比较困难。尤其在液滴精确尺寸未知或液滴形状偏离理想形状的情况下[5-7]，难以采用液滴轮廓模拟拟合的方法进行接触角的测量分析。为此，拟探索基于液滴局部轮廓的接触角测量方法。理论上，作为液滴局部表面与固体表面的力学关联参数，接触角理应可通过液滴局部轮廓形状的拟合来测量计算。

在接触角测量中，除了测量方法本身所引入的误差外，液滴轮廓与表面接触点的不确定性也将引入一定的接触角测量误差。李健等[8]研究发现，在接触角接近180°时，测量基线(接触点)位置的半个像素偏差将导致7°的接触角测量误差；Liu等[9]研究发现测量基线位置的一个像素偏差将导致15°的接触角测量误差，之后研究进一步对测量基线引入的误差开展了较为系统的研究[10]。因此，在所提出的测量方法中，接触点或基线的移动对测量结果的影响也需要做相应考虑。

为了实现接触角测量，现提出基于液滴局部轮廓的接触角测量方法，通过超疏水表面上的液滴接触角测量实验对提出的方法进行实验验证，探究提出的测量方法的稳定性和有效性，讨论测量方法中对测量点的选择原则，并考察该方法中基线选择误差对接触角测量结果的影响程度，以期为表面润湿性能研究提供可靠的接触角测量方法。

1 研究方法

1.1 基于液滴局部轮廓的接触角测量方法

所提出的基于液滴局部轮廓的接触角测量方法原理如下：采用液滴局部轮廓的3个测量点(其中一个是液滴轮廓与表面的接触点)拟合成圆弧；基于拟合的圆弧，通过公式可计算出圆弧在接触点位置的切线斜率；根据计算出来的斜率可计算出液滴的接触角。

根据测量方法的原理，对图1所示的液滴局部轮廓，通过轮廓上的3个点A、B、C可确定轮廓圆弧的圆心O，由此可确定出OA的斜率。由于在测量中表面处于水平状态(即基线为水平线)，而过A点的液滴轮廓切线与OA垂直，根据OA的斜率可计算出接触角。为推导出接触角的计算公式，在液滴轮廓的A点建立坐标系，则圆弧方程为

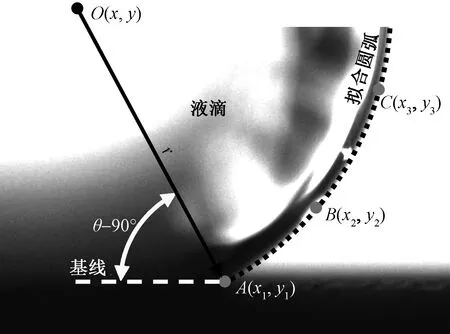
图1 基于液滴局部轮廓的接触角测量方法示意图

(1)

式(1)中：(x,y)为圆弧圆心O的坐标；(x2,y2)为圆弧上一点B的坐标；(x3,y3)为圆弧上一点C的坐标。根据方程(1)，可求出圆弧圆心O的坐标为

(2)

接触角θ满足关系：

tan(θ-90°)=-y/x

(3)

根据式(3)可推导出接触角的计算公式为

θ=arctan(-y/x)+90°

(4)

测量时，首先确定液滴轮廓与基线的接触点位置A，并以A为基准测量出液滴轮廓上不相同的两点B和C的坐标(x2,y2)和(x3,y3)，将测量结果代入式(2)计算出圆弧圆心O的坐标(x,y)，再将(x,y)代入式(4)即可计算出接触角θ。

1.2 测量方法的验证实验

为了验证本文方法，对两个超疏水表面上的液滴接触角进行测试，考察接触角计算结果随所选择的测量点位置的变化情况。实验中所采用的材料为300 μm厚的单面抛光硅片，先后通过酒精和去离子水超声清洗。对清洗后的表面采用激光直写加工方法进行加工，所使用的激光器为最大功率为20 W的纳秒光纤激光器，加工功率设置为13 W，脉冲频率设置为20 kHz，透镜焦距254 mm，激光波长1 064 nm，激光光斑直径聚焦后约50 μm，脉宽约240 ns，扫描速度为200 mm/s。加工时聚焦激光束沿交叉网纹路径扫描以去除材料，两样品上的网纹线条间距分别设置为60 μm和80 μm，加工幅面为10 mm×10 mm，每个样品加工2次。样品加工后再进行氟化处理可获得超疏水表面[11]。

表面形貌采用扫描电子显微镜(FEI NovaNano 450，美国)观察，样品表面上的液滴图像通过自制的简易接触角测试平台采集，为了模拟无标尺的测量情况，将采集图片导入Getdata软件以获取液滴轮廓点。

2 结果与讨论

2.1 样品测试结果

图2为样品表面形貌，可以看出，激光加工可产生表面微凸起阵列，对这样的表面进行氟化处理降低表面自由能后可获得超疏水表面[11]，水滴在表面上的接触角大于150°。样品上的测试水滴(水滴体积为3 μL)如图3所示，可以看出，液滴在表面上具有较大的接触角。为了测量液滴的接触角，将采集的液体图片导入到Getdata软件，在该软件里以软件自带的网格为单位来度量拾取点坐标，拾取液滴局部轮廓上的若干测量点，后续分析所拾取的测量点序列如图4所示。同时通过软件拾取液滴轮廓最高点和液滴轮廓与表面的左右两接触点，用以计算基于量高法的接触角。

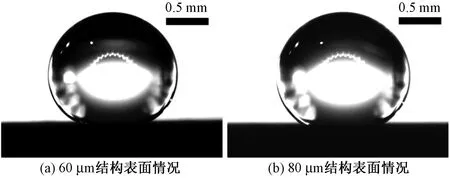
图3 超疏水表面上的液滴图像

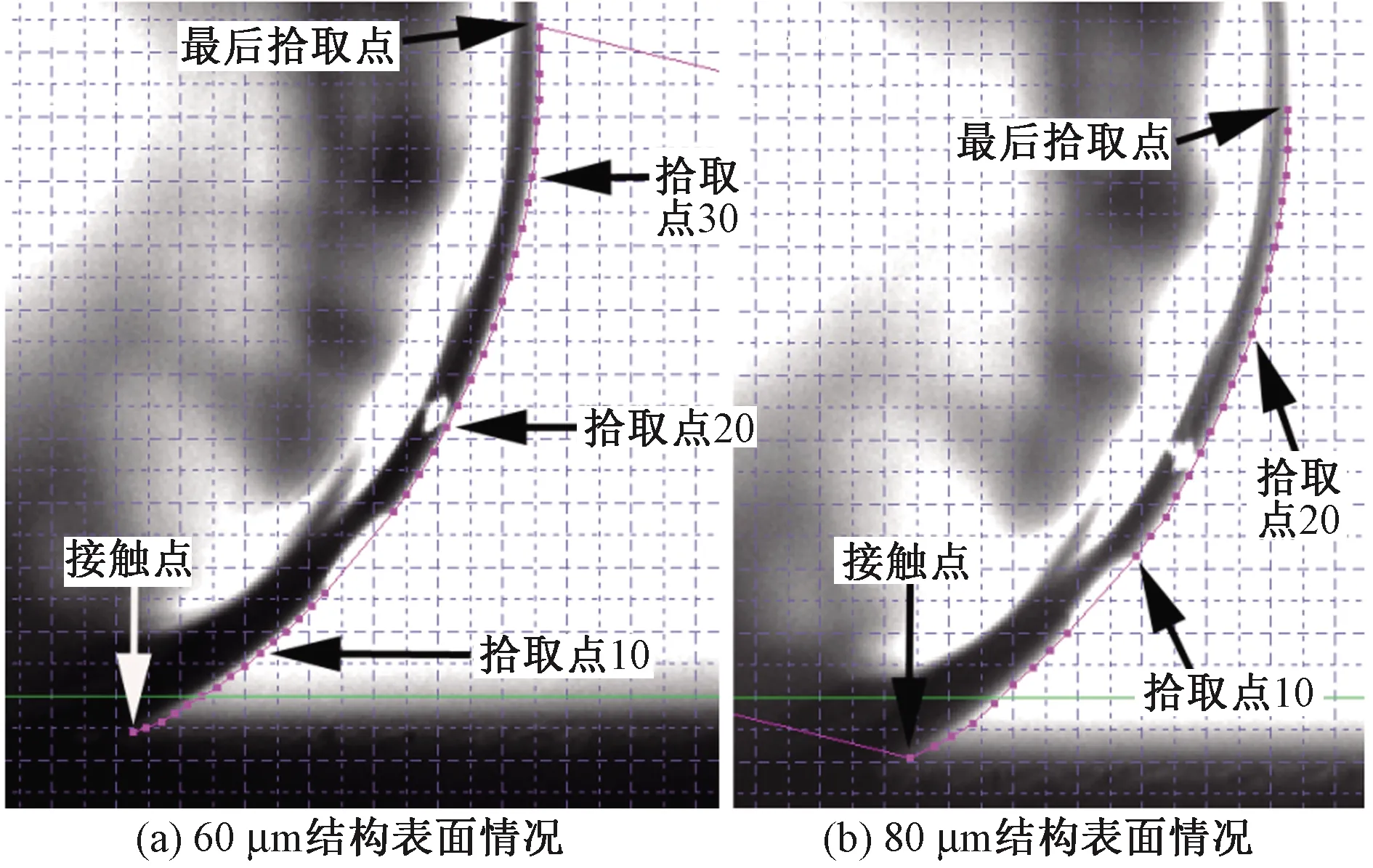
图4 液滴局部轮廓上拾取点的情况

基于量高法的接触角计算公式为

θ=2arctan(2h/w)

(5)

式(5)中：h为液滴的高度(液滴轮廓最高点到接触点的垂直距离)；w为液滴与表面的接触区域直径(两接触点之间的距离)。

由式(5)可知，测量接触角只需测量出液滴的高度和液滴与表面的接触区域直径即可计算出接触角，测量极为方便。基于拾取的液滴轮廓点，采用量高法计算出的两样品上的液滴接触角分别为144.4°和139.4°。根据文献[2]，量高法的测量结果具有较大的偏差(大于5°)，需要采用更合理的测量方法。

2.2 基于液滴局部轮廓的接触角测量的稳定性和有效性

图5为所提出的基于液滴局部轮廓的接触角测量方法的计算结果。以轮廓与表面的接触点A为原点，图4中轮廓上最后拾取点为固定测量点C，另一测量点B从原点开始沿轮廓上的拾取点逐次测量，依据式(2)和式(4)的接触角测量计算结果如图5(a)所示，可以看出，当测量点接近原点时，拾取点的误差将对测量计算结果产生较大的影响，接触角波动较大。实际上，由于液滴在接触点附近受表面微结构影响，轮廓可能偏离理想的轴对称液滴轮廓，而且接触点附近拾取点的微小误差会导致较大的测量误差[8-9]，所以一般接触角测量中都依据全局的液滴轮廓模拟拟合结果来计算接触角。测量点从第5拾取点开始，接触角的计算结果趋于稳定，对微凸起周期为60 μm表面，接触角为153°±1°，对微凸起周期为80 μm表面，接触角为149°±1°。可以看出，基于液滴局部轮廓的接触角测量结果比采用量高法得到的结果大10°，而文献[2]中对于液滴体积为3 μL的情况，150°真实接触角通过量高法测量的结果为144°，本文结果与文献[2]预测结果吻合较好。本文结果与文献[2]预测结果偏差的原因在于：文献[2]是将液滴理想化为旋转对称形状，而实验的液滴形状除受表面张力的影响外，还受到测试表面的作用。对于所使用的网纹状微沟槽表面，网纹并非旋转对称，尤其在测试点附近，液滴轮廓会在一定程度上偏离理想轮廓，此时将液滴理想化为旋转对称形状与真实情况有偏差。同时，由于所使用的网纹状微沟槽表面接触点之间的间距w可能变大，导致采用量高法测量的接触角偏小。

为了考察基于液滴局部轮廓的接触角测量方法的稳定性，采用了接触点A和中间拾取点C(样品1采用第15拾取点，样品2采用第10拾取点)为固定测量点，改变第三测量点进行测量以计算接触角，计算结果如图5(b)所示。从图5(b)中可以看出，测量点选取为第5拾取点以后的接触角结果趋于稳定，接触角依然分别为153°±1°和149°±1°，而且采用固定测量点以后的测量点测量的结果更稳定。由此可以得出结论，采用的测量点不同时，接触角计算的结果稳定。

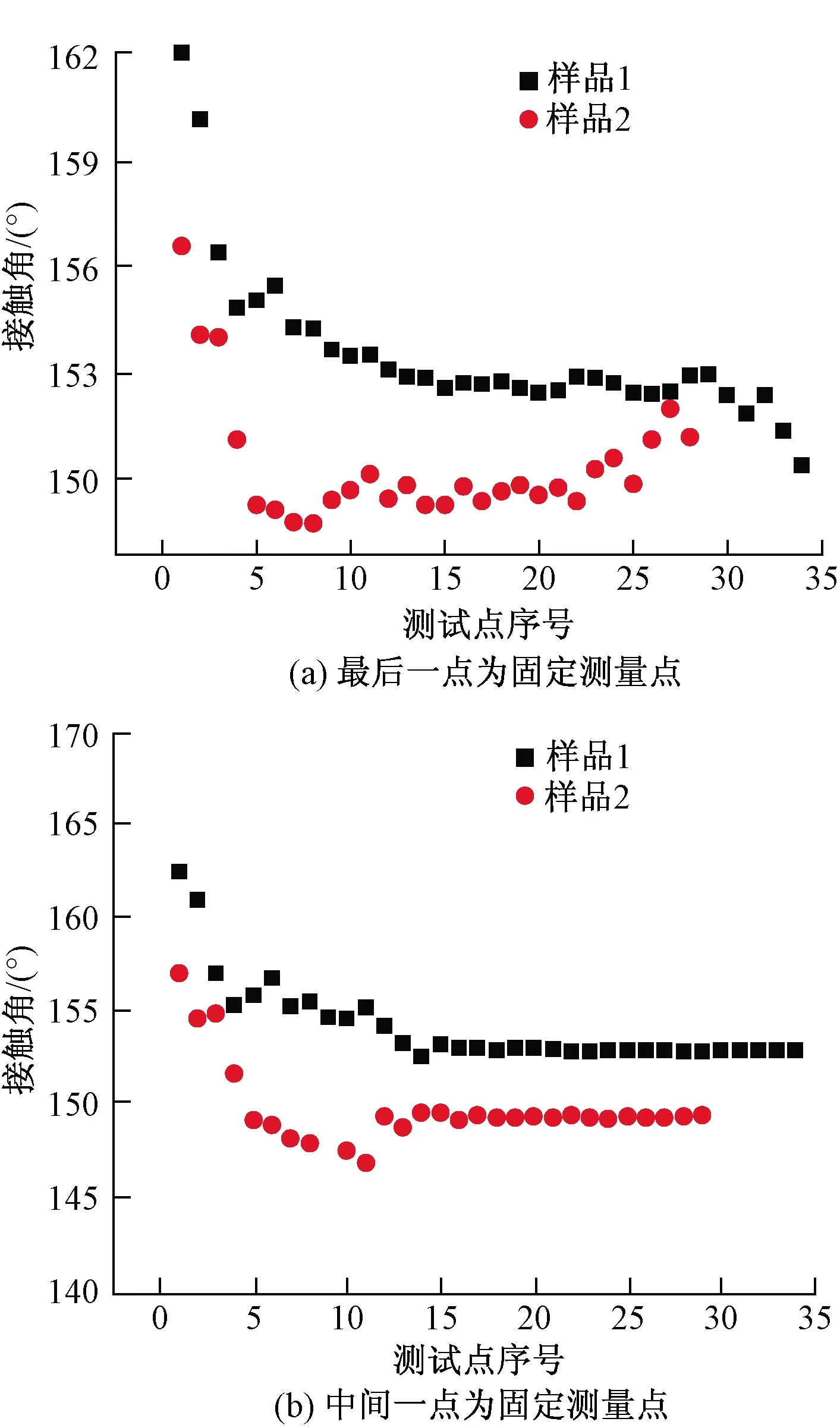
图5 基于液滴局部轮廓的接触角测量计算结果

图6对基于液滴局部轮廓的接触角测量方法和量高法的测量结果进行了比较，可以看出，以量高法的测量结果(144.4°和139.4°)作切线，该切线与液滴轮廓的相切的位置明显偏离接触点，而采用本文方法的测量结果(153°和149°)作的切线与液滴轮廓相切于接触点，这说明了本文方法的有效性。

图6 基于液滴局部轮廓的接触角测量方法与量高法的比较

为了探究基于液滴局部轮廓的接触角测量方法可靠性的根源，考察了拟合的圆弧半径和圆弧圆心随选取测量点的变化情况，如图7所示，可以看出，对于中部的测量点(测量点序号在10～25)，拟合的圆弧半径[图7(a)]比较稳定，此时的圆弧圆心稳定在局部区域。由于拟合圆弧圆心的位置稳定[图7(b)的内嵌图内圆弧圆心分布范围小]，即图7(b)中的曲率半径r稳定，由此决定的接触角θ的测量稳定性较好。

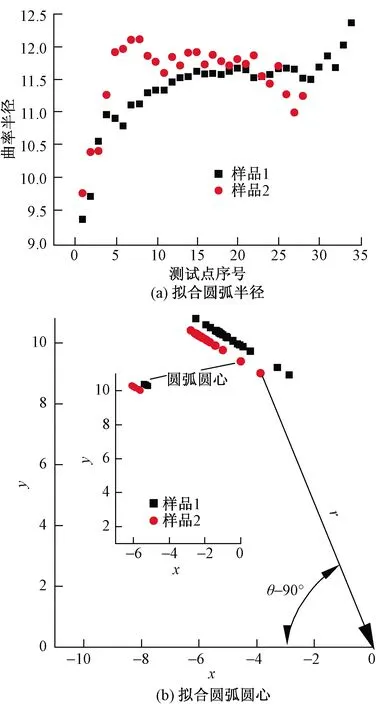
图7 拟合圆弧参数随测量点的变化

2.3 液滴局部轮廓测量点的设定原则

在前述的结果中，选择不同测量点得到不同的测量结果，测量点B靠近接触点A时，接触角的测量结果波动较大，而测量点B远离接触点A则接触角逐渐过渡到量高法的结果，为此，在测量计算时需要设定合理的测量点。根据式(2)，选定接触点A为固定测量点后，当其他测量点B或C接近接触点时，即(x2,y2)或(x3,y3)的值较小，式(2)分母的值较小，此时拾取测量点时引入的误差将影响拟合圆弧的曲率半径[图7(a)]，因此以上的结果(图5)中测量点B靠近接触点A时接触角波动较大，出现失真。当两测量点B(x2,y2)和C(x3,y3)相距较近时，式(2)的分母也较小，也会引入一定的误差。根据以上分析，在确定测量点时，需要将测量点均匀分布在轮廓上，如图8(a)所示，让测量点之间的间距满足AB≈BC。图8(b)为根据这一原则对前述的液滴轮廓进行计算得到的接触角测量值，可以看出，测量点B为第7拾取点时接触角达到稳定，接触角的测量结果仍然为153°±1°和149°±1°。参考图4中的拾取点位置可知，此时测量点都处于液滴高度的1/4范围之内，因此建议该方法实施中测量点选定为液滴高度2/5范围内的局部轮廓上，且两测量点与接触点均布在该局部轮廓上。由于本文的测量方法基于液滴的局部轮廓，该方法可适用于两表面间的受压液滴[5-6]和失真液滴[7]的接触角分析。

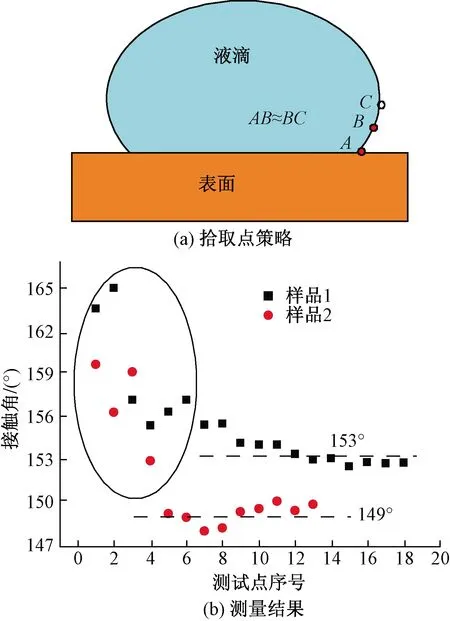
图8 近等间距测量点选择策略及实验结果

2.4 基线选择对测量结果的影响

在李健等[8]和Liu等[9]的研究中，基线的移动将导致较大的接触角误差，其中，李健等[8]发现，接触角接近180°时，半个像素的接触点误差将导致7°的接触角偏差；而Liu等[9]的研究表明，接近180°时，一个像素的接触点误差(基线上移或下移一个像素)将导致15°的接触角偏差。为探索本文方法中接触点选取误差对测量结果的影响，将接触点设定为第二拾取点，固定测量点为最后拾取点，考察第3测量点选取为不同拾取点时的接触角计算结果。接触角计算结果如图9所示，可以看出，对于样品1，由于接触点选择误差(接触点从第1拾取点移动到第2拾取点)影响，接触角测量结果的变化趋势与前述的变化趋势有差别，测量结果的稳定性不是太理想，但接触角基本在153°±2°的范围，说明接触点的误差并未对接触角结果产生较大影响；而对于样品2，接触角测量结果为147°±2°，比原始的测量结果小了2°。参考图4可知，对两样品测量结果的差别在于接触点偏差大小，样品1中第2拾取点和真实接触点相距较近(但远大于1像素)，接触角测量偏差较小，而样品2中第2拾取点与接触点相距较远，接触角测量偏差为2°。因此，本文方法中接触点误差所引起的测量误差可控，在实际测量中，可通过提高接触点在水平方向上的精度来提升接触角测量精度。

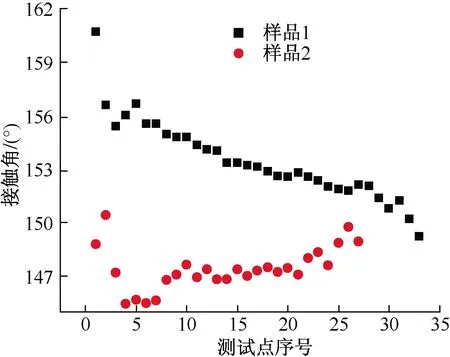
图9 接触点误差对接触角测量结果的影响

3 结论

为了实现接触角测量，提出了基于液滴局部轮廓的接触角测量方法，对该方法进行了实验验证，得出以下结论。

(1)基于液滴局部轮廓的接触角测量方法能有效稳定地测量出超疏水表面上的液滴接触角值。

(2)在实施基于液滴局部轮廓接触角测量方法时测量点需要选取在液滴高度的2/5范围内，且3个测量点近似均布在此范围的液滴轮廓上。

(3)基于液滴局部轮廓的接触角测量方法中接触点的选择误差对接触角测量结果的影响是可控的，可通过提高接触点在水平方向上的精度来提升测量精度。