基于卡尔曼滤波的实时总电子含量周跳探测与修复

罗逸楠，蔡红涛，高顺祖

(武汉大学电子信息学院，武汉 430072)

全球定位系统(global position system，GPS)作为美国国防部研制，能够适应全天候的无线电导航具有很高的精度[1]、成本费用低、有很好的时效性的特点。而电离层中的总电子含量(total electron content，TEC)的测定对于GPS导航定位会产生一定的影响[2]。除此之外在载波相位测量时，由于整周模糊度和周跳的存在，造成该过程中准确性出现偏差，因此周跳的探测与修复问题在高精度导航定位系统是一个亟待解决的问题[3]。自20世纪80年代以来，已经引发无数中外学者对此问题的关注，并提出了TurboEdit法、高次差法、多项式拟合以及小波变换法等解决方法[4]，结果证明这些传统周跳探测修复方法在一定程度上取得了较好的效果但都存在其不足之处。TurboEdit法易受到原始数据的干扰，无法探测6周以内的周跳[4]；多项式拟合法对小周跳的探测很不灵敏[5]；高次差法无法彻底消除噪声问题[6]；小波变换法则不能探测周跳的真实值[7]。近年来，中国学者提出了新的改进方法。孟令东等[8]提出了将小波变换联合伪距相位组合的方法，进一步提高了计算跳变量的数值稳定性；王力等[9]利用历元间差分观测值进行参考站探测周跳避免了伪距噪声的影响；赵松克等[10]利用多项式和多普勒组合的方法改善了探测的误差性；刘国超等[11]将双频载波相位求差法应用其中，有效解决了周跳值解算多解的问题。虽然这些方法都进行了创新和改进，但仍不能完全适应于随时可能发生强扰动的电离层环境中，尤其考虑到周跳现象会对TEC变化产生影响，上述方法仍无法很好解决随机出现小周跳以及造成TEC不再连续变化后的探测与修复问题。

针对上述问题，提出了基于相位电离层残差(phase ionospheric residual，PIR)的组合Kalman滤波算法进行周跳检测及修复。针对电离层研究TEC变化情况下，采取差分载波相位技术的(relative total electron content，RTEC)充当实测数据的探测量，然后再利用Kalman滤波对检测到的周跳进行修正。最后通过武汉站和桂林接收机观测站得到的实测数据进行检验，进一步验证本文方法的有效性。

1 基本原理

1.1 周跳及其对TEC的影响

周跳是一种常见的现象，一般多发生于全球导航卫星系统(global navigation satellite system，GNSS)中，由于载波相位测量技术过程中，卫星信号会由于失锁现象使得整周计数在某个时间历元发生跃迁甚至是中断消失[12]。因此对于这一现象进行探测及修复研究具有重要意义[13]。

作为GPS当中主要的观测量，载波相位以及伪距相比而言，前者的测量在精度上有着更好的效果。然而在载波相位测量时，整周模糊度以及周跳现象存在，在一定程度上会对相位测量的准确性造成影响。一般来说，对于没有出现任何问题的GPS载波相位，其实际观测值包括整周以及小数部分二者共同组成。在测量过程中，其中的小数部分由于载波相位的特性通常可以较为精确地测量出来，但是相位整周数的变化是由多普勒积分累计计算得到，所以很容易在实际观测中受到周跳的影响。

对相位的整周数这一情况，则需通过信号的跟踪以及整周计数部分的实际情况来进行考虑。图1中出现在相位观测中的一个周跳现象。在500时间历元时相位由于某种原因出现了一个跳变，造成理论观测值和实际观测值出现了一个偏差，而且会影响接下来时间历元中的观测现象，这个过程就是出现了一个典型的周跳现象。

图1 相位观测值中的周跳

理论上，载波相位观测值φ可表示为

φ=a+int(φ)+Fr(φ)

(1)

式(1)中：a为初始的整周未知数；int(φ)为整周计数；Fr(φ)为不足一周的小数部分。

在载波相位观测过程中，对于历元间的整周计数如果由于意外发生了中断现象，则当调整好计数之后会丢失这些数据，造成了计数错误，然而对于式(1)中的小数部分Fr(φ)并不会随之发生错误，它仍会保持正确变化，周跳现象也就因此而产生。

对于周跳现象发生在不同情况下有多种因素所致，一般包括如下方面。

(1)由于传播环境例如电离层不规则结构对信号的散射作用或者吸收作用导致的信号强度的深度衰落，以及载波相位的快速起伏。

(2)如果信号的传播路径上存在建筑、树木等障碍物遮，那么将会对信号造成影响进而引起信号的中断。

(3)再则如果接收机内部结构存在有限的动态范围，或者锁相环带宽导致的信号失锁都会引起周跳的产生。

周跳的影响是存在于各方面的，一方面会对观测数据质量产生严重的干扰；另一方面对于GPS导航、定位以及测量精度等都会存在一定的限制。所以对于周跳的各种问题自始至今是学者们关注的焦点，特别是对于周跳的探测以及修复尤为关键[14]。同时由于载波相位发生了突变，计算得到的TEC也会相应地出现随机跳变，产生严重的误差。图2为电离层强烈扰动时观测到的周跳的一个示例，示例中的数据选取为2019年3月21日在桂林站对GPS 10号卫星观测所得，图2中显示3月21日02：00—06：00由于多次出现了周跳，造成了TEC频繁的间断和突跳，而非是正常的连续变化。

图2 周跳对卫星TEC观测结果的影响示例

1.2 差分载波相位测量TEC的方法

当一列初始相位为φ0的波在介质中传播，经过时间t传播了一段距离，此时，该波的相位变为

(1)

式(1)中：φ为相位；ω为波的角频率；c为光速；f为波的频率；np为相折射指数；N为电子的电荷量；TECs为传播路径上的总电子数；φ0为波的发射时初始相位；S为接收机以及卫星两者之间几何距离。

由于GPS信标L1和L2的载波频率不同，因此当出现载波频率不同的两列波，其相位不能直接进行比较，为了利用双频差分相位法获得TEC，需要进行频率归一化，即将不同频率的载波相位归一化为共同的基频fs上，此时可定义差分载波相位为

(2)

式(2)中：m1=f1/fs=154；m2=f2/fs=120，其中，f1为信标L1的载波频率，f2为信标L2的载波频率，fs为归一化后的基频，fs=11.23 MHz，φ1为信标L1的波相位改变量；φ2为信标L2的波相位改变量。

由式(2)可以计算得到φ1和φ2，同时代入上述定义中可得

(3)

式(3)中：Δφ为差分载波相位；Δφ0为初始相位差，进一步可得

(4)

式(4)中：TEC0为一个常数，它由初相位以及整周模糊度两者共同组成。

从式(4)可以看出，利用双频差分载波相位测量得到的TEC与实际TEC之间相差一个常数，这个常数的值无法精确确定。换句话说，无法经过测量得到绝对TEC。因此一般采取差分载波相位技术用相对总电子含量(relative total electron content，RTEC)表示。在进行这个测量过程中，载波相位的电离层残差组合充当实测数据的探测量，其随时间历元的波动即可表示为RTEC的变化。

2 基于Kalman滤波的周跳探测与修复算法

2.1 卡尔曼滤波

L1和L2两个频率信号可能会一起出现失锁以及周跳，同时也可能仅一个频率出现失锁和周跳。实际上，相对于L1来说，L2的频率信号更可能会发生周跳或者是失锁现象。但是相对于电离层的研究来说，更关注TEC的变化，不需要区分L1和L2信号的周跳值。

因此可以采用基于相位电离层残差(phase ionospheric residual，PIR)的组合Kalman滤波算法进行周跳检测以及修复，采用此种方法对存在的周跳RTEC数据能够得到较为理想的处理结果。

相对于PIR的组合Kalman滤波来说，从本质上来讲其仍是基于状态空间模型，利用递推的形式对系统的输入和输出进行统计的最小方差估计算法[15]。在这个过程不仅需要考虑系统的过程噪声的统计特性，还不能忽视测量噪声可能产生的影响，因此在对于多维的非平稳的随机过程中，该算法具有很好的实效性。

首先，假设系统的状态方程为

xk=φk,k+1xk-1+wk-1

(5)

式(5)中：xk为系统在k时刻的n维状态向量；φk,k+1为系统的n维状态转移矩阵；wk-1为系统在这个过程中所产生的噪声序列，同时这个序列符合均值为零，满足协方差矩阵Qk符合多元正态分布，即wk～N(0,Qk)，其观测方程为

yk=Hkxk+vk

(6)

式(6)中：Hk为n维观测矩阵；vk为均值为零，协方差矩阵为Rk的服从正态分布的n维观测噪声序列，即vk～N(0,Rk)。

同时，假设初始状态以及每一时刻的噪声{x0,w1,w2,…,wk,v1,v2,…,vk}均为相互独立的存在。

将这个过程的观测量输入进滤波器中，卡尔曼滤波主要利用观测过程中噪声的统计特性[16]，其实际将估计值(即系统的状态参数)作为中间滤波器的输出项。同时，利用时间系统的自动更新联合对观测值的更新算法，对该系统输入以及输出端进行比较和联系，当系统输入新的观测值时，状态估计和状态估计的误差随即进行更新，原则上按照时间更新和测量更新的方程进行分类，其滤波的递归方程如下。

首先，按照时间更新方程，可表示为

(7)

(8)

按照测更新后的方程为

(9)

(10)

(11)

式中，Q为系统噪声；E表示求均值；kk为先验值和新的测量值之间的相对权重的一个卡尔曼增益；Yk为测量后更新的观测值；pk为更新后的误差协方差矩阵；R为协方差矩阵；＾ 表示估计值;～表示第k次迭代的先验值;通常选取用来衡量xk的估计精度的正定矩阵pk来表示，为xk对应的协方差矩阵；I为单位矩阵；kk为在先验值和新的测量值之间的相对权重的一个卡尔曼增益，且相对估计值在测量值的噪声比相对较大的情况下，卡尔曼增益使算法对新的观测值并不是很敏感，反之，如果当估计状态相对于观测值精确度并非精准时，卡尔曼增益则会使得该算法对新观测的数据值更加敏感。如果利用系统方程(或者动态方程)以及观测方程估计出所有需要处理的信号，则可以将周跳现象当作是载波相位观测量的一种噪声，利用这一算法进行转化，可搭建其周跳探测以及修复模型[17]。

2.2 周跳探测模型

本文模型采取Kalman滤波算法，其原理本质上利用最小方差的估计[18]。对于给定的观测系统，对其输入或者输出观测数据进行最优的估计。然而在这个过程中，观测数据仍会存在系统噪声以及干扰，这将对其造成影响，所以这个滤波的过程即为最优估计的过程。

在利用差分载波相位测量TEC时，根据公式计算可知测量得到的TEC与实际TEC的值之间只相差一个常数。此时，将采取探测量表示为这个残差组合，相当于观测RTEC的变化[19]，利用对RTEC的变化的影响检测周跳的探测和修复效果。

利用做差法对观测方程进行计算，计算公式公式为

φ=λL1φL1-λL2φL2

(12)

式(12)中：φ为探测量的残差组分；λL1和λL2分别为信标L1和L2的载波波长；φL1和φL2分别为信标L1和L2的相位。假设采样间隔为T，由于PIR以及消去几何项、钟差、多径效应等，只剩下电离层残差项。此时更高阶差分项则将会趋近于0[20]，对于任何一段历元，对PIR采取用三次多项式模型，同时将φk+1在φk处泰勒展开可得

(13)

将状态值记为

Xk=(φk,φ′k,φ″k,φ‴k)T

(14)

由式(14)可建立卡尔曼滤波的状态模型为

Xk+1=AXk+Guk

(15)

式(15)中：uk为模型误差；A为状态转移矩阵；G为系数矩阵；根据φk+1在φk处泰勒展开可分别得到A和G的表达式为

(16)

测量方程为

φk=CXk+zk

(17)

式(17)中：zk为误差，其方差为σ2；C为系数矩阵，C=(1,0,0,0)。

记Xk滤波值为X(k|k)，其中k为第k次迭代，滤波误差方差阵为P(k|k)，Xk+1预报值表示为X(k+1|k)，预报误差方差矩阵表示为P(k+1|k)，此时滤波的预测方程为

X(k+1|k)=AX(k|k)

(18)

P(k+1|k)=AP(k|k)AT+GQGT

(19)

测量值修正后可表示为

X(k|k)=X(k|k-1)+Mk[φk-CX(k|k-1)]

(20)

式(20)中：Mk为相对权重的卡尔曼增益，可表示为

Mk=P(k|k-1)CT[R+CP(k|k-1)CT]-1

(21)

(22)

ek=φk-CX(k|k)

(23)

式(23)中：ek为观测值与预报值之间的残差值。

2.3 周跳检测与修复流程

周跳的检测和修复在实例中，首先设置滤波器初始值为

X(0|0)=(φ0,φ1-φ0,φ2+φ0-2φ1,φ3+3φ1-3φ2-φ0)T

(24)

(25)

对于检测周跳主要分为如下3个步骤，关键在于利用Kalman滤波进行修复，流程图如图3所示。

Jk为增益矩阵；u为探测阈值，取u=4μ，其中μ为测量值的标准差；Vk预报残差值

步骤1首先计算Kalman滤波值X(k|k)：①确定滤波启动的初始条件，此时k=1；②利用包括式(23)之前的方程计算得到预报值、增益矩阵、预报误差方差阵；③利用计算方程式得到并储存状态滤波值X(k|k)、滤波误差方差阵、包括观测到的滤波值φk=CX(k|k)，当k=k+1时，返回②部分进行直至最后一个观测数据出现。

步骤2预测下一时刻状态值，同时选取当前的滤波器进行滤波：①固定区间预测的预测方程为

X(j|k)=Aj-kX(k|k),j>k

(26)

式(26)中：Aj为在j时刻的状态转移矩阵；②利用i-1历元的滤波值X(i-1|i-1)进行预测可得到方程为

X(i+1|i-1)=Al+lX(i-1|i-1),l≥0

(27)

式(27)中：Al为在l时刻的状态转移矩阵。

步骤3周跳的检测与修复，采用预报残差法：①设定探测阈值为4μ，与此同时将计算所得到预报残差与阈值进行比较，比较后可知如果|ek|>4μ，表示在该范围内发生了周跳现象，得到的周跳值即为预报残差ek；②进行周跳的消除[22]，将观测值加上ek；③然后以当前历元为起点，重新设置滤波器参数，重复步骤1。

3 周跳检测和修复结果

由上述卡尔曼滤波的周跳探测模型介绍可知，为了验证Kalman滤波算法的有效性和可靠性，分别进行模拟周跳探测和实测数据的周跳修复。

3.1 模拟周跳的探测

首先选取一段“干净”且没有跳变的实际观测数据，计算其载波相位电离层残差组合作为“理论值”，然后利用人为因素在载波相位的随机历元中添加随机大小的跳变，同样地计算电离层残差组合，得到含有模拟周跳的观测值，利用提出的周跳算法对其进行探测和修复，与此同时选择比较模拟和探测的周跳值的大小，将修复后的观测值与理论值进行对比，进而分析本文算法的有效性及精度值[23-24]。

选取武汉站的接收机作为第一个站点，该接收机于2018年8月19日观测到北斗B01卫星的数据，同时为了尽可能多地去消除多路径和卫星失锁的影响，将其截至仰角设置为60°，可以得到十分“干净”的数据。在载波相位L1和L2中随机加入了模拟周跳，为了突出Kalman滤波算法对小型周跳的探测能力，特意设定了几组典型的比较小的周跳，然后使用该算法进行探测和修复，加入周跳的历元和大小以及探测到的周跳值如表1所示，其中，人为添加的模拟周跳均为整周数，即1周、2周、3周；而用载波相位的电离层残差组合充当实测数据探测量后，此时探测到的周跳单位为m，可以看出，所有的加入模拟周跳之后的历元都能成功探测，并且其探测的误差均小于0.015 m。

从表1可以看出，给出的几个比较典型的小周跳探测的结果，实际对应比较大的周跳时，已经有更成熟的方法进行更为精确的修复，因此在实际应用中，通常采用的是二级探测的方法，先使用载波相位减去伪距的方式探测并进行修复大于6周的周跳，然后再采用Kalman滤波算法探测较为小的周跳，随后也进行了一些模拟探测，并统计了探测误差，转换成TEC单位后的方差为0.005 4 TECu，其中误差分布如图4所示。从图4中的数据走势分布可以看出，总体上基本符合高斯分布。

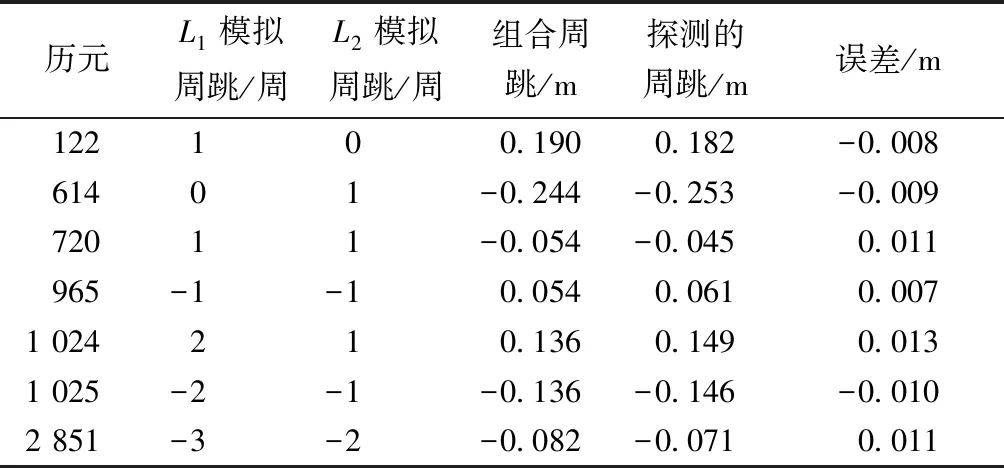
表1 模拟周跳的探测表

图4 模拟周跳探测残差分布

3.2 周跳探测和修复实例

图5、图6为两个实例所使用的数据是2019年3月2日在桂林观测站观测得到的GPS 5号(图5)和GPS10号(图6)卫星的数据，对此进行周跳探测以及修复。可以看出，图5(a)、图6(a)是由双频载波相位实测数据计算得到的RTEC数据；利用修正后的数据对比[图5(b)、图6(b)]可以看出，无论是GPS 5号卫星还是10号卫星，在0～10 000 s历元这个时间段里，这两颗卫星的RTEC数据中都出现了多次短暂的失锁和明显的周跳现象，从而使得RTEC变化不连续，尤其是GPS 5号卫星即使在10 000～20 000 s历元这个时间段里仍然存在很严重的数据短暂缺失和周跳现象。而图5(b)中的黑色散点为TEC随时间的变化，两条红线则分别作为根据计算得到的变化范围，如果黑色散点落在红线之内表示没有出现周跳现象。

为了能够更清楚显示两者之间的变化关系，图5、图6中将纵坐标的变化范围限定在0附近，可以看出，当RTEC变化是平滑的时候，两条红线相距很近，而当RTEC开始出现较大的变化时，它们之间的距离相应变宽，使得这种周跳探测及修正方法可以同时适用于电离层平静条件和有电离层不规则结构存在的情况。

sTEC为倾斜总电子含量；ΔTEC为RTEC(即相对TEC)的变化率；TECu为TEC的单位，1 TECu≈0.104 m

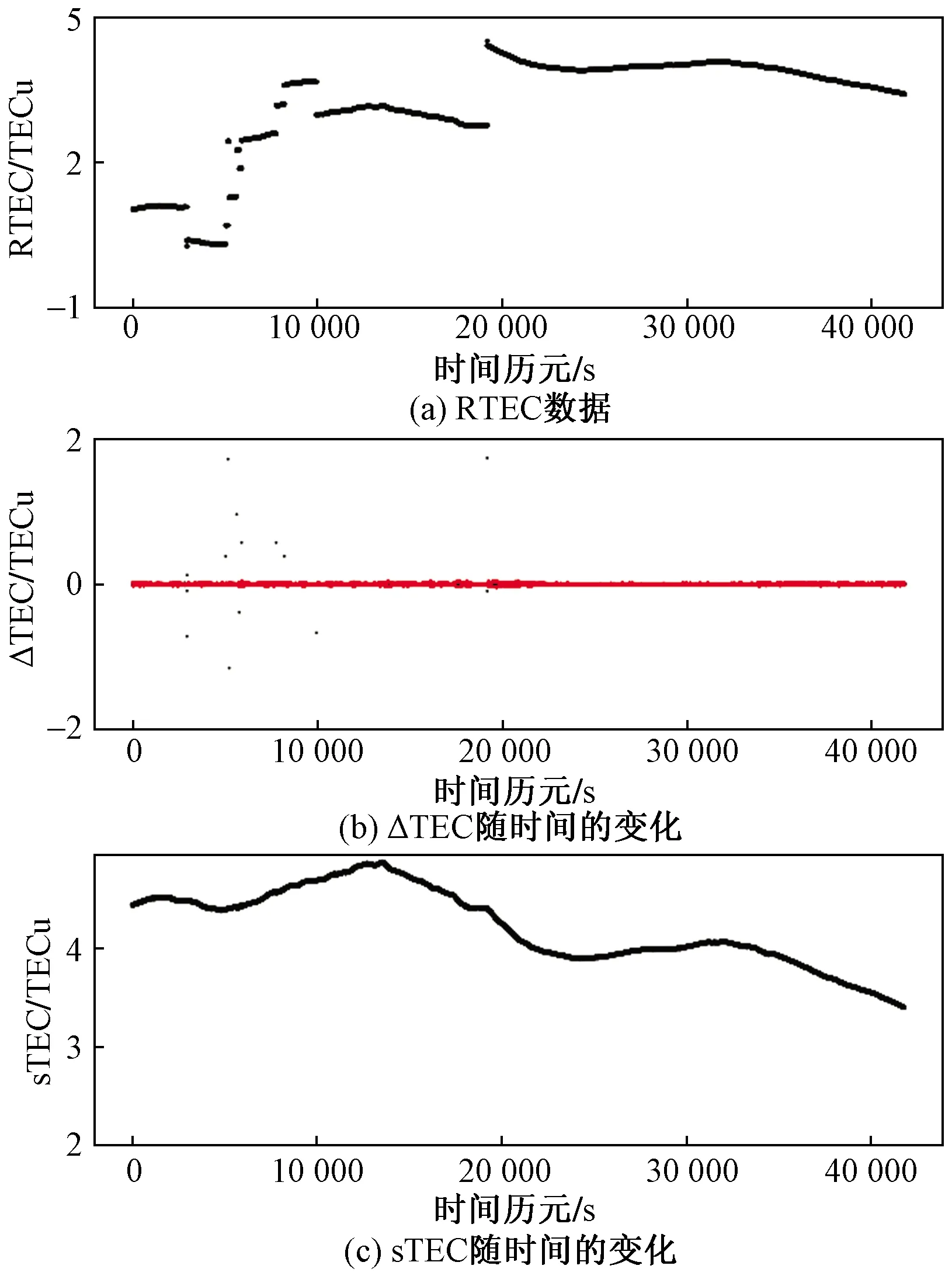
图6 模拟周跳的检测与修正数据图(GPS 10 卫星数据)

在这两个实例中，这两颗卫星在0～20 000 s历元之间有两段时间变化明显变大，第一段时间0～10 000 s历元RTEC出现多次周跳，而第二段时间10 000～20 000 s历元则没有，相应地在0～10 000 s历元有很多散点不在这两条红线之间，但是10 000～20 000 s历元则基本都落在了两条红线之间。因此利用桂林观测站观测得到的实测数据很好地证实了本文方法切实可行。

4 结论

探讨了电离层领域的理论研究中周跳现象的存在、产生的原因及可能产生的影响。针对传统周跳探测修复方法的不足之处，提出基于Kalman滤波的实时TEC周跳探测与修复方法，探测不同的观测数据类型及其组合，利用双频差分载波相位测量。同时采取差分载波相位技术用RTEC代替无法经过测量得到绝对TEC，并将修复后的观测值与理论值进行对比。选取了2018年8月19日武汉站的接收机观测到的北斗卫星的数据进行模拟周跳的探测，最后利用2019年3月2日在桂林观测站观测得到的实测数据进行检验，结果验证了该方法的有效性。通过分析研究和实验验证，得到如下结论。

(1)周跳的存在会造成TEC出现了频繁的间断和突跳，不再连续变化。对周跳探测以及修复时，即使是小周跳，Kalman滤波算法也有很好的探测效果，实测数据验证其探测的误差均小于0.015 m。而对于小周跳的探测效果从残差分布可以看出总体上基本符合高斯分布，更加表明该方法的切实可行。

(2)在进行实际观测数据的对比分析可以看出，由于周跳使得RTEC变化不连续时，利用Kalman滤波算法可以明显优化和减少此类现象的发生，无论是在微弱扰动还是剧烈的环境下进行数据处理，都能高效完好的对随机发生的周跳现象进行探测识别以及修复工作。

(3)实例试验是基于桂林站的接收机的数据来进行的，并未考虑不同的地区和更长的时间的情况。同时该算法的精度可能受实际应用场景和观测数据密集程度等多种因素的影响，因此，如果为了达到详细的分析对比，则需要进行下一步更加完善的实验设计。