第三系粉细砂土双轴压缩细观破坏机制数值模拟分析
王立伦
(中铁十九局集团 第三工程有限公司, 辽宁 沈阳 110136)
0 引言
近年来,我国学者对于土体的研究成果较为丰富.王艳丽等[1]采用GDS三轴试验系统对饱和砂土进行了一系列的固结不排水动三轴试验,分析了不同围压下饱和砂土的动力特性.苏永奇等[2]对青藏铁路粉质黏土进行了动三轴室内冻融循环试验,分析了不同试验条件下土样各力学参数的变化规律.杨周洁等[3]以南海北部沉积物土样为参考,制备同级配粉细砂,并通过自主研发的含水合物沉积物三轴试验系统对制备的粉细砂进行了三轴剪切试验.白琴琴等[4]在不同地区取回土样制备了多组不同含水率的砂土试样,并通过三轴压缩试验、直剪试验以及基质吸力试验对土样进行了测试,分析了土样的力学参数随含水的分布规律.毛海涛等[5]采用三维颗粒流数值模拟软件对不同围压及含水率条件下非饱和土的细观参数之间关系进行了研究,并结合室内试验进行了对比分析.刘小文等[6]基于PFC3D建立非饱和土的之间试验模型,以颗粒之间黏结强度为桥梁来模拟不同基质吸力和固结应力下非饱和土的力学特性.周凤玺[7]等采用三维离散元数方法对非饱和土进行了三轴固结不排水数值模拟研究,采用Hill模型来考虑土体颗粒之间的相互作用.李可宇等[8]基于颗粒流方法对红黏土进行了大量三轴固结不排水三轴试验,分析了粘结强度、摩擦系数、刚度比和孔隙率等细观参数的变化对应力-应变曲线的影响.
综上可知,已有土类材料的研究取得了显著成果,但对土样内部细观特征的研究相对较少.本文采用颗粒离散单元法对不同围压下的第三系粉细砂土进行双轴试验数值模拟研究,分析不同围压下试样内部的速度场、位移场以及裂隙演化规律.
1 离散元模型建立与参数标定
1.1 离散元模型建立
本文采用二维离散元数值计算软件(PFC2D)建立高80 mm、宽39.1 mm的标准长方形试样如图1所示,图中颗粒颜色代表不同粒径大小.颗粒间接触本构模型采用接触黏结模型,以位移控制方式进行加载.首先,上下左右4面墙体同时以0.03 mm/s的移动速率对试样均匀施加围压,待围压达到预定值后保持恒定,上下两端墙体继续以0.03 mm/s的加载速率对试样进行加载直至试验结束.由于围压作用下土体在三轴压缩条件下会出现应变硬化现象,因此,试验终止条件由轴向应变决定.一般情况下,当轴向应变达到15%时,认为试样完全破坏.为分析不同围压下第三系粉细砂土的细观特征变化规律,本文设置围压分别为50、100、150、200 kPa.
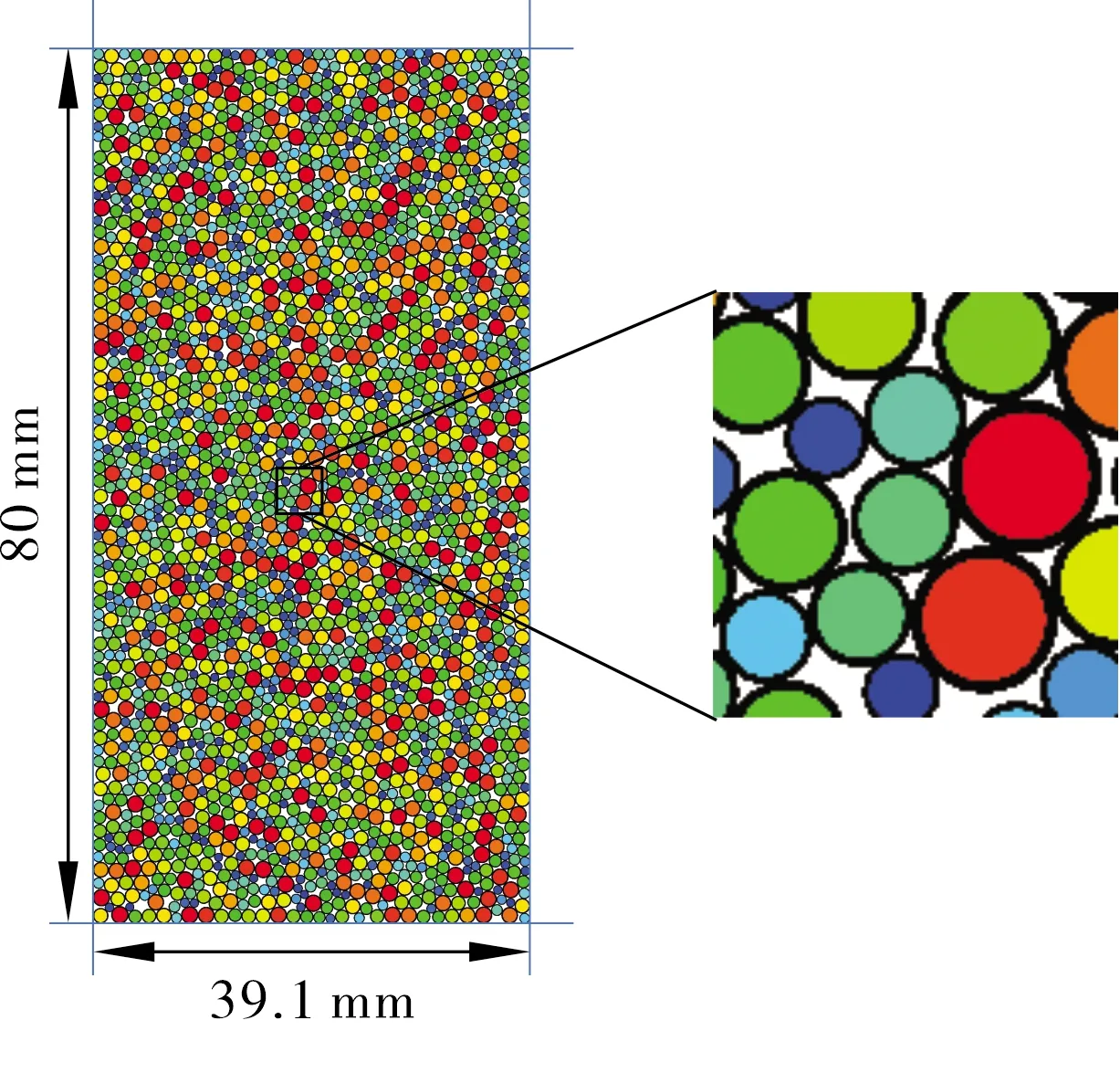
图1 第三系粉砂土双轴压缩数值模型
1.2 参数标定
在PFC中,数值模型宏观力学行为取决于细观参数,包括颗粒粒径、接触黏结模量、接触黏结强度及黏结刚度比等,不同的细观参数对峰值强度、弹性模量和泊松比等具有显著影响.为了尽可能的与室内试验应力-应变曲线相接近,需要对建立的颗粒流模型进行参数标定.第三系粉细砂土自施工现场,运至实验室后制得高80 mm、直径39.1 mm的圆柱试样.采用GDS多功能土体三轴试验系统对粉细砂土试样进行单轴压缩试验,试验加载速率及围压等控制条件与离散元数值模拟保持相同,通过室内试验获取土样的应力-应变曲线及宏观力学参数,根据已有研究成果,初选一组近似参数进行单轴压缩数值试验,并基于“试错法”反复调整数值模型的细观参数,最终获得近似满足粉细砂土宏观力学特性的细观参数,如表1所示.

表1 路基土细观参数
2 试验结果分析
2.1 试验曲线分析
图2为基于离散元数值模拟得到的第三系粉细砂土双轴压缩应力-应变曲线和体积应变-轴向应变曲线.从图2(a)中可以明显看出,不同围压下粉细砂土均表现出应变硬化特征,应力-应变曲线可大致分为2个阶段,当轴向应变小于2%时,试样处于线弹性阶段,当轴向应变大于2%时,试样处于塑性屈服阶段.定义轴向应变为15%处所对应的偏应力为峰值强度,则粉细砂土试样的峰值强度呈明显增大趋势.
从图2(b)中可以看出,粉细砂土试样的体积变形呈明显的规律性变化.当围压较低时,试样先表现为先剪缩后剪胀,例如,当围压为50、100 kPa时,试样由剪缩转为剪胀时对应的轴向应变分别为5.14%和10.08%.当围压较高时,试样仅表现出剪缩特征.可见,围压能够有效限制试样的剪胀变形,一定程度上起到保护试样的作用.
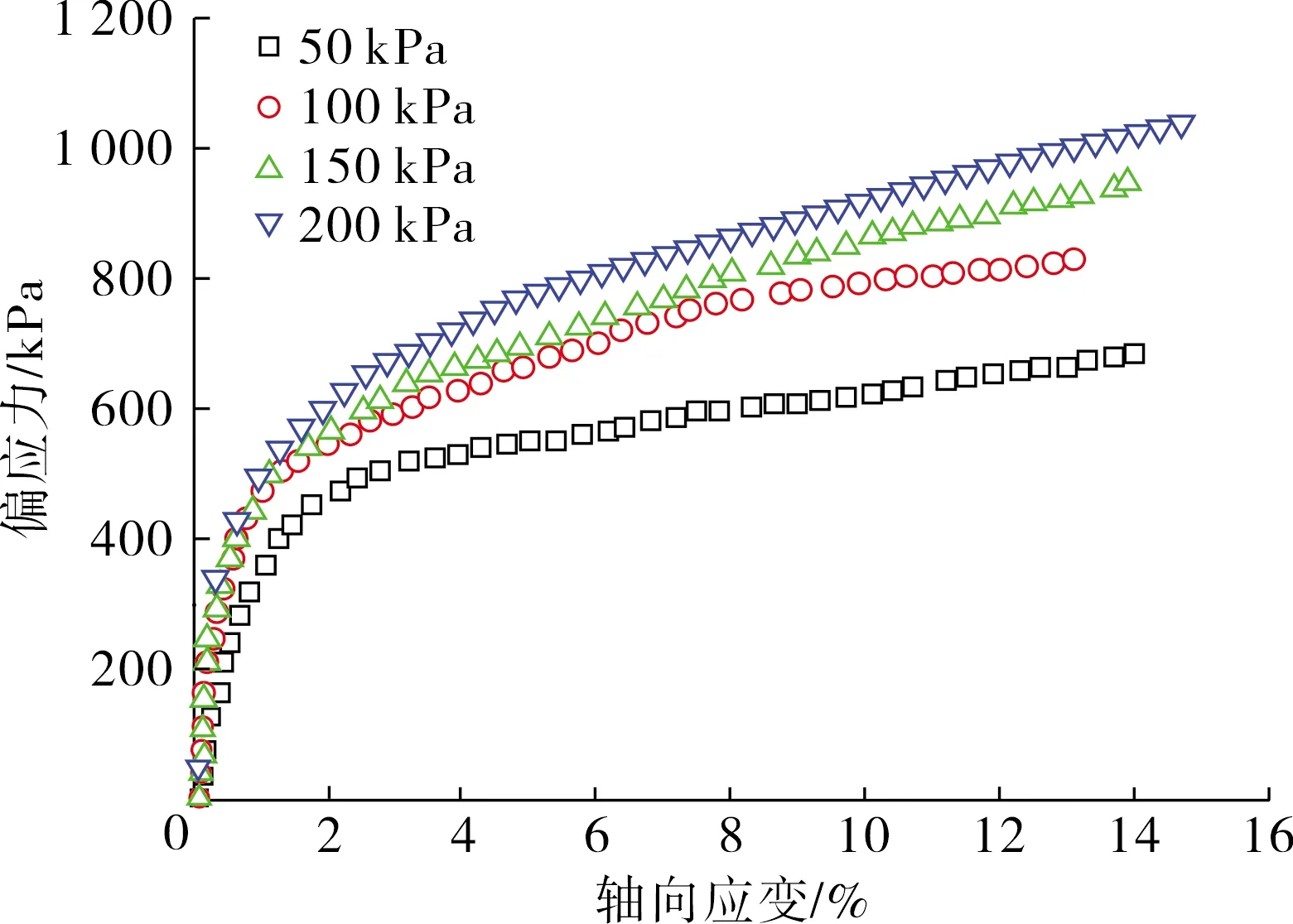
(a) 偏应力-轴向应变
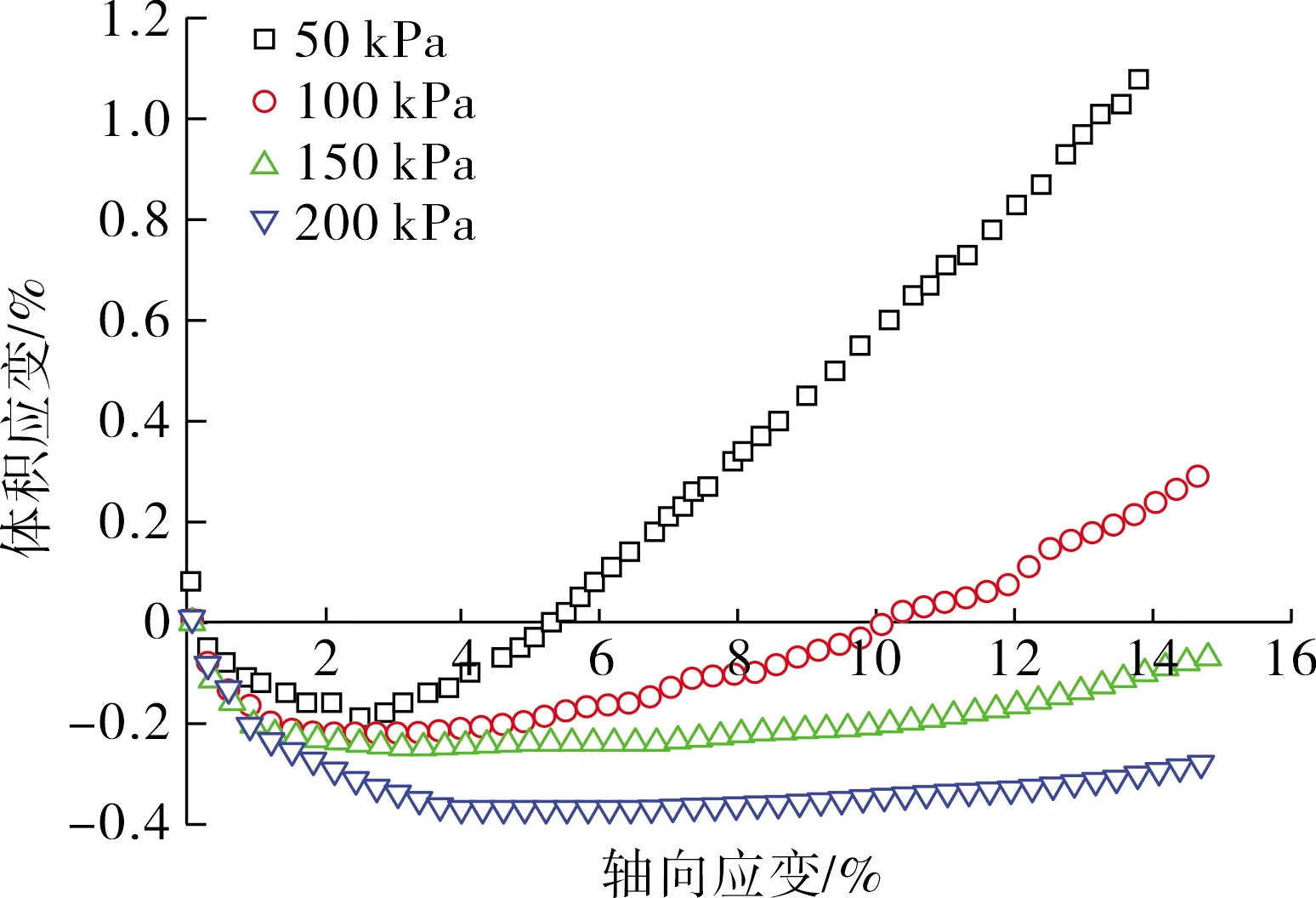
(b) 体积应变-轴向应变图2 试验曲线
2.2 细观特征分析
图3为轴向应变15%时不同围压下粉细砂土离散元数值试样的速度场矢量图,图中颗粒的速度方向由箭头表示,颜色由浅变深代表速度由大到小.从中可以看出,试样的速度场呈规律性变化.当围压较低时(例如50、100 kPa),试样内部产生一条明显的剪切带,随着围压的逐渐增大,剪切带逐渐消失,表明围压的增大能够改变试样的破坏模式.从图中还可以看出,不同围压下试样内部颗粒速度大小变化均为由内到外逐渐增大.沿试样中间位置做一条竖线,能够明显看出竖线左右两侧颗粒速度场方向相反.
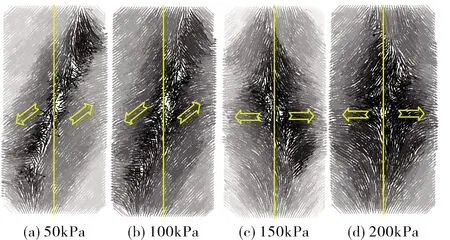
图3 不同围压下粉细砂土速度场矢量图
图4为不同围压下轴向应变为15%时粉细砂土离散元数值试样的位移云图.从图中可以明显看出,不同围压下试样内部颗粒位移的变化情况大体相同,均为中间位移变化量最小,边缘位移变化量最大,且随着围压的逐渐增大,试样边缘位移较大区域逐渐减少,中间位移较小区域逐渐增大,表明围压越高越能够限制试样的变形.从图中还可以看出,不同围压下的粉细砂土试样内部均形成了一条明显的剪切带,且随着围压的逐渐增大,试样的剪切带与水平方向的夹角逐渐减小,剪切带逐渐增大.这一点与速度长表现处的规律略有差异,原因是速度场在试验结束时颗粒速度方向随机分布,受外力影响后随时改变方向,而位移场则是颗粒运动结束后产生的位置变化,受外力影响相对较小.
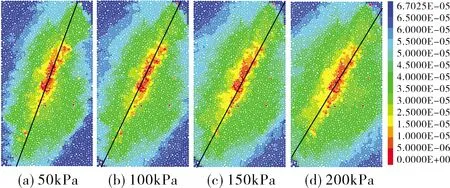
图4 不同围压下粉细砂土位移场云图(单位:m)
提取不同围压剪切带与水平方向的夹角,并绘制其随围压的分布曲线如图5所示.可以看出,随着围压的逐渐增大,第三系粉细砂土的剪切破坏角呈逐渐递减趋势.当围压为50 kPa时,试样的剪切破坏角为71.01°,当围压分别为100、150、200 kPa时,试样的剪切破坏角分别减小了7.06%、11.03%和13.65%,虽然剪切破坏角在逐渐减小,但减幅同样在缩小.采用Origin软件对曲线进行拟合发现,试样的剪切破坏角与围压之间满足指数函数关系,曲线斜率逐渐减小,二者之间拟合相关度在0.95以上,表明二者之间具有良好的相关性.
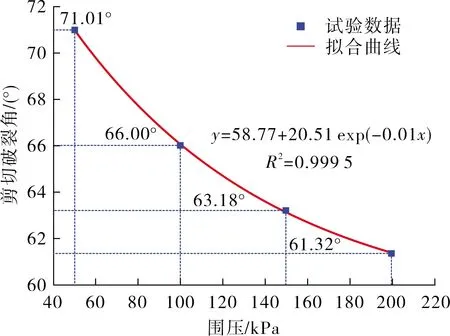
图5 剪切破坏角与围压之间关系
图6为不同围压下粉细砂土离散元数值试样内部裂隙数随轴向应变的分布曲线.从图中可以看出,随着围压的逐渐增大,相同轴向应变情况下试样内部裂隙数量逐渐增多.当围压为50 kPa时,第一条裂隙产生时的轴向应变为7.21%,当围压分别为100、150、200 kPa时,对应的第一条裂隙产生时的轴向应变分别为5.73%、4.87%和3.65%,可见,围压越高,试样内部产生第一条裂隙对应的轴向应变越小.
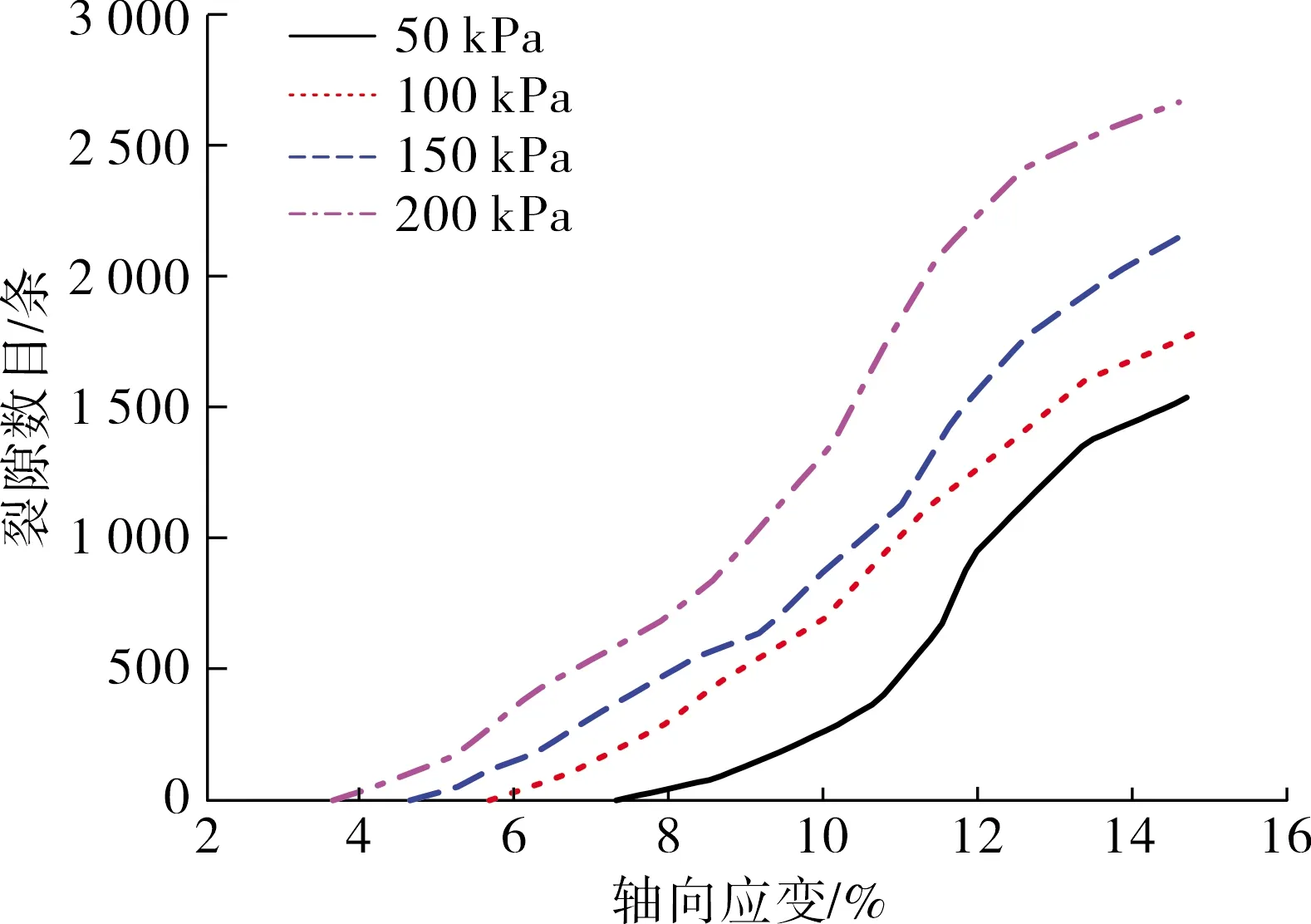
图6 不同围压粉细砂土裂隙演化曲线
3 结论
1) 通过细观参数标定,找到了满足本文胡麻岭隧道第三系粉细砂土的细观力学参数.
2) 根据离散元数值模拟结果,不同围压下粉细砂土均表现出应变硬化特征,且围压越高,峰值强度越大.当围压较低时,试样表现出剪胀变形,当围压较高时,试样表现出剪缩变形.
3) 根据数值模拟结果,不同围压下颗粒速度变化情况大体相同,均为中间小边缘大;位移场同样表现出中间小两边大,不同的是在位移场中均出现一条明显的剪切带;随着围压的逐渐增大,试样内部产生第一条裂隙对应的轴向应变逐渐减小,相同轴向应变条件下,围压越高,试样内部裂隙越多.
4) 随着围压的逐渐增大,第三系粉细砂土的剪切破坏角呈逐渐递减趋势,且减幅同样在缩小.试样的剪切破坏角与围压之间满足指数函数关系.

