铁路路基粗粒土填料累积变形试验研究

江 杰，陈思达，罗方正，彭伯伦，欧孝夺

(1.广西大学土木建筑工程学院，南宁 530004；2.广西大学工程防灾与结构安全教育部重点实验室，南宁 530004；3.广西大学广西防灾减灾与工程安全重点实验室，南宁 530004；4.中国建筑第八工程局有限公司，南宁 530000)

随着中国铁路建设的快速发展，长期列车荷载作用下路基的累积变形问题越来越受到重视。粗粒土因其优良的工程特性，常常被用来作为路基填料，用来承受上部结构传递的列车荷载，而路基的累积变形与土体的应力状态、性质等条件有关[1-3]。

目前用来预测土体累积变形的方法有弹塑性本构模型和经验模型两种，弹塑性本构模型虽然更为合理，但计算过于复杂；相比之下，经验模型是基于试验数据，采用拟合的方式直接获取累积变形与各影响因素之间的函数关系，使用方便因而得到广泛应用。Barksdale[4]通过试验发现土体累积应变呈现渐进增长规律，用半对数模型与试验结果拟合较好。但是，Monismith等[5]通过试验发现半对数模型在荷载振动次数较多的试验中对结果的拟合偏差较大，因此又提出了指数模型。Baladi等[6]也通过试验提出了类似的累积应变预测模型。Sweere[7]进一步通过试验验证了指数模型的正确性，该模型得到了进一步发展。指数模型的优点有参数少、计算过程简单，但也因此带来了一些局限性，不能够反映一些土体特性。后来有Li等[8]对指数模型进行改进，把土体初始应力的影响考虑在内，在建立预测模型时引入了静强度的概念，能够更好地反映土的实际工程特性，但也因此使得计算参数的增多。赵春彦等[9]在对上海地区饱和软土进行动三轴试验的过程中，将等效循环动应力的影响考虑在内，基于试验成果，建立了一个能够考虑多个参数的软黏土累积应变预测模型。周文权等[10-11]对粗粒土进行一系列的动三轴试验，试验条件包括不同的动应力幅值、围压以及含水率，并由试验结果提出了相应的累积应变预测模型。蔡袁强[12]等通过试验研究了不同荷载频率下粗粒土路基填料的长期动力特性。崔高航等[13]研究了冻融循环作用下的软土累积变形规律，依据试验结果，建立了一个对数模型用以预测冻融循环作用下软土累积变形。蒋红光[14]指出，即便铁路路基产生的沉降在规范允许范围内，也会引起轨道不平顺。综上所述，粗粒土累积变形由多种因素共同决定，建立多因素影响下的粗粒土累积应变预测模型对实际工程中路基动力变形控制具有十分重要的指导意义。

为了研究粗粒土填料在长期循环荷载下的累积变形规律，利用GDS公司动三轴试验设备开展饱和不排水试验，研究了围压、动应力比、压实度和荷载循环次数对粗粒土累积应变规律的影响。并结合试验结果，提出了一个能够合理描述粗粒土累积应变发展的经验公式，为铁路路基沉降变形的预测与控制提供参考依据。

1 试验方案

1.1 试验设备

试验所使用的仪器为GDS动三轴系统，如图1所示，可进行试样直径为38、50、70、100 mm的试验。该系统主要由驱动装置、压力室、围压控制器、反压控制器、信号调节装置以及高速数据采集和控制卡或轻型控制系统组成。

图1 GDS动三轴试验设备

1.2 试验材料

本试验所用的土样由土、砂、碎石等组成，筛分后的试验土样如图2所示，该土样的一些基本物理指标如表1所示，按照《公路土工试验规程》[15]中的规定，对于100 mm的试样，最大允许粒径为试样直径的五分之一，即本试验最大允许粒径为20 mm，原土样中不符合该粒径的颗粒，采用规范推荐的等量替代法进行替换，替换前后的颗粒级配曲线如图3所示。依据《铁路路基设计规范》[16]中对于填料的分类，该土样不均匀系数Cu=14.25，曲率系数Cc=0.70，属于B组填料。

图2 试验土样

图3 颗粒级配曲线

表1 土样基本物理性质指标

1.3 试验方案

试样直径为100 mm，高度为200 mm，在最优含水率条件下制成。由于实际路基填料介于完全排水条件和完全不排水条件之间，而不排水条件下路基破坏的可能性更大，出于安全性考虑，本次试验采用了不排水方式。铁路路基表面的动荷载一般在13～100 kPa范围内[17]，采用循环动应力比(cyclic stress ratio，CSR)来表示动荷载大小，定义动应力比CSR为动应力幅值和2倍围压σ3的比值。为了突出压实度K的影响，特选取压实度0.85、0.9作为对照组。试验荷载频率为1 Hz，固结比为1。本次试验相关参数取值见表2。

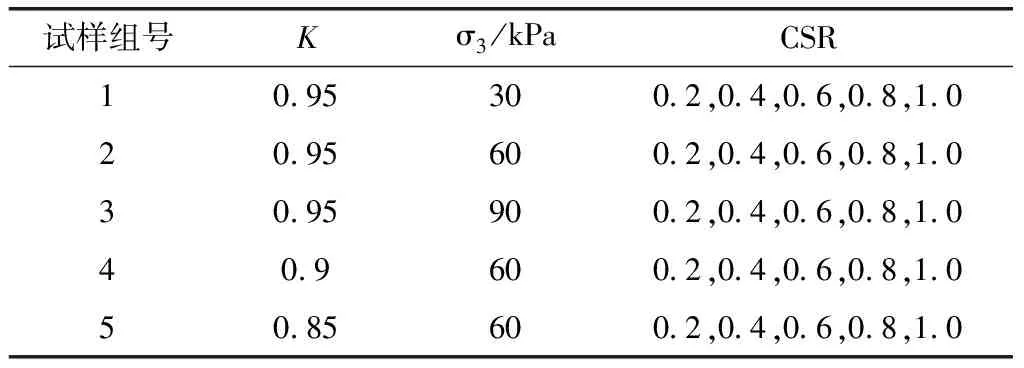
表2 试验方案

式样的制备在室温下进行，将土样风干过筛去掉粒径大于20 mm的颗粒，然后按照试验所需的含水率配比，本次试验土样均在最优含水率下制作，称取相应重量的土样和水充分混合，将土样搅拌好后放置24 h。利用制样模具筒进行试样的击实，为了保证试样的击实效果，将每个试样分成5层进行击实，每层高度为40 mm。每层击实后需将表面进行刮毛处理在开始击实下一层，通过控制每层的质量制备出试验所需压实度的试样。击实完成后，试样先采用抽真空饱和，抽气2 h后注水并静置24 h。然后再进行反压饱和，待孔压水压力系数B超过0.95，即可进行固结。固结完成后，开始施加动荷载，本次试验采用应力控制的加载方式，每个试样分级加载，施加的动荷载类型将采用的是如图4所示的一维正弦波循环荷载。一共进行了5组试验，每组试验包括5个试样。

图4 试验加载曲线

2 试验结果及分析

2.1 动应力比CSR对累积应变的影响

为了研究动应力比对试样轴向累积应变εacc的影响，图5表现了压实度为0.95、围压为60 kPa，不同动应力比条件下的轴向累积应变与荷载振动次数的关系曲线。从总体趋势上看，所施加荷载的动应力比越大，土体总累积应变和荷载加载初期的应变发展速率就越大。在加载初期，累积应变快速发展，在荷载振动次数N=1 000次时的累积应变就已经达到最终应变的75%左右，随着动荷载的继续施加，土体越来越密实，应变发展速率迅速减少，每一个荷载循环所产生的累积应变越来越小，最后累积应变会达到一个稳定值。此外，在压实度K=0.95、σ3=60 kPa的条件下，CSR=1.0时的累积应变是应力比为0.2时的4.29倍，可见动应力比的影响非常显著。

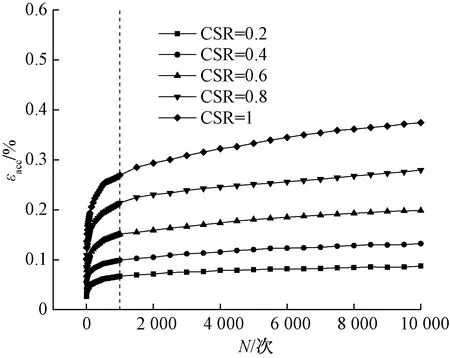
图5 不同CSR下累积应变与振次的关系曲线

2.2 围压对累积应变的影响

为了研究不同围压对试样轴向累积应变的影响，图6表现了压实度为0.95、动应力比为0.6、围压分别为30、60、90 kPa条件下的轴向累积应变与荷载振动次数的关系曲线。总体趋势上看，前1 000振次下轴向累积应变快速发展，轴向累积应变随着围压的增大而增大。在相同应力比条件下，对于3种围压条件，在10 000振次下的累积应变分别为0.132%、0.200%、0.230%，涨幅为1.52倍和1.15倍。可见围压对土体的累积变形也有一定程度的影响。

图6 不同围压下累积应变与振次的关系曲线

2.3 压实度对累积应变的影响

为了研究不同压实度对试样轴向累积应变的影响，图7是围压为60 kPa、动应力比为0.6、压实度分别为0.85、0.9、0.95条件下的轴向累积应变与荷载振动次数的关系曲线。从图7看压实度对累积应变的影响还是非常明显的，轴向累积应变随着压实度的增大而增大。在10 000次的荷载振动作用下，不同压实度的累积应变分别为0.295%、0.263%、0.200%，压实度为0.9的试样比压实度为0.85的试样累积应变减少了大约10.85%，而压实度为0.95的试样比压实度为0.9的试样累积应变减少了23.95%。

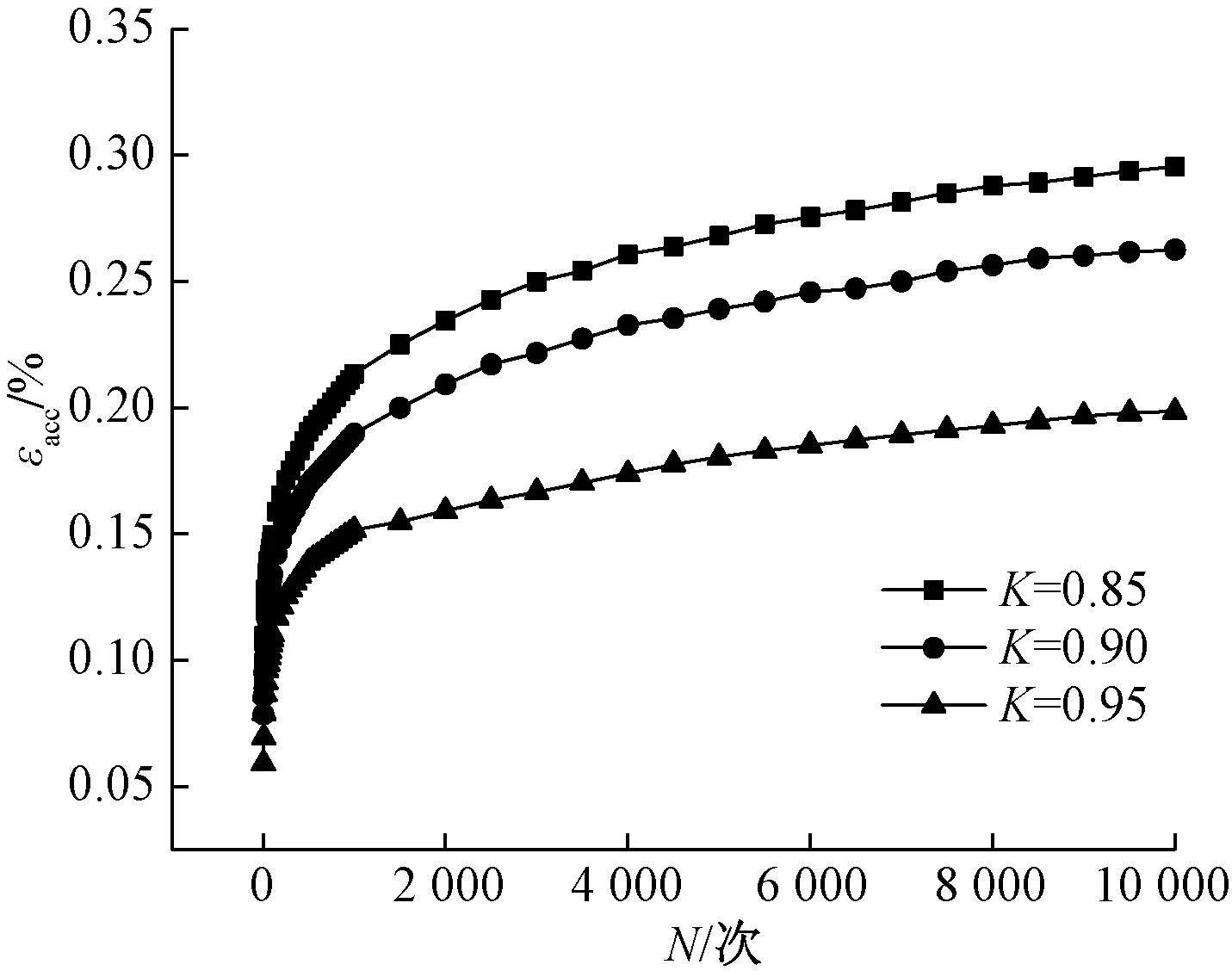
图7 不同压实度下累积应变与振次的关系曲线

3 累积应变模型

3.1 累积应变模型的建立

通过上面的研究可以发现，土体长期累积变形受到动应力比、围压和压实度等多种因素的影响，较少的模型参数会增加拟合的离散性，所以本文提出的累积应变模型由4个影响函数组成，假设这些影响因素相互独立[18]，建立一个由多个影响函数组成的累积应变模型为

εacc(N)=fCSRfσ3fKfN

(1)

式(1)中：fCSR、fσ3、fK、fN分别为动应力比、围压、压实度和荷载振动次数的影响函数，其表达式为

fCSR=A1eCSR×B1+C1

(2)

(3)

fK=A3K-B3

(4)

(5)

式中：A1、A2、A3、A4、B1、B2、B3、B4、C1、C2、C4为拟合参数。

通过迭代分析法确定影响函数的表达式，具体步骤如下。

(1)选取适合的函数fCSR、fσ3、fK分别拟合累积应变与动应力比、围压和压实度之间的关系。将压实度为0.95、围压为60 kPa及不同循环应力比试验条件下的数据按照函数fCSR进行拟合，将压实度为0.95以及围压为30、60、90 kPa下循环应力比为0.6时的试验数据按照函数fσ3进行拟合，将压实度为0.95、0.9、0.85以及围压为60 kPa下循环应力比为0.6时的数据按照函数fK进行拟合，这里选取的试验数据为第50、100、500、1 000、1 500、3 000、6 000、9 000次循环加载下的数据。

(2)将所有试验数据除以第一步得到的fCSR、fσ3、fK就可以得到只与振次有关的累积应变εacc(N)/fCSRfσ3fK，接着选择一个合适的函数fN拟合累积应变与振次的关系。

(3)下一步进行迭代，将第一步中用来拟合函数fCSR的试验数据除以fσ3、fK、fN即可得到只与动应力比有关的累积应变εacc(N)/fNfσ3fK，然后重新拟合就可以得到关于函数fCSR新的拟合参数。同样的，对函数fσ3、fK中的拟合参数进行迭代更新。直到前后两次迭代过程中的累积应变变化小于1.0%，则完成迭代，否则返回(2)。

按照上述的处理方法，最后得出的归一化累积应变与动应力比、围压、压实度和荷载振动次数之间的关系如图8～图11所示，可以看到归一化后的数据基本上都聚集在一个狭窄的区域中。函数拟合结果见表3所示。

表3 模型参数

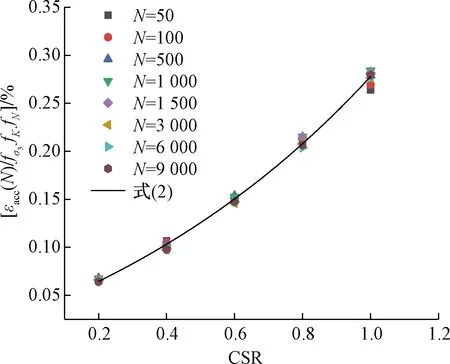
图8 累积应变的动应力比影响系数

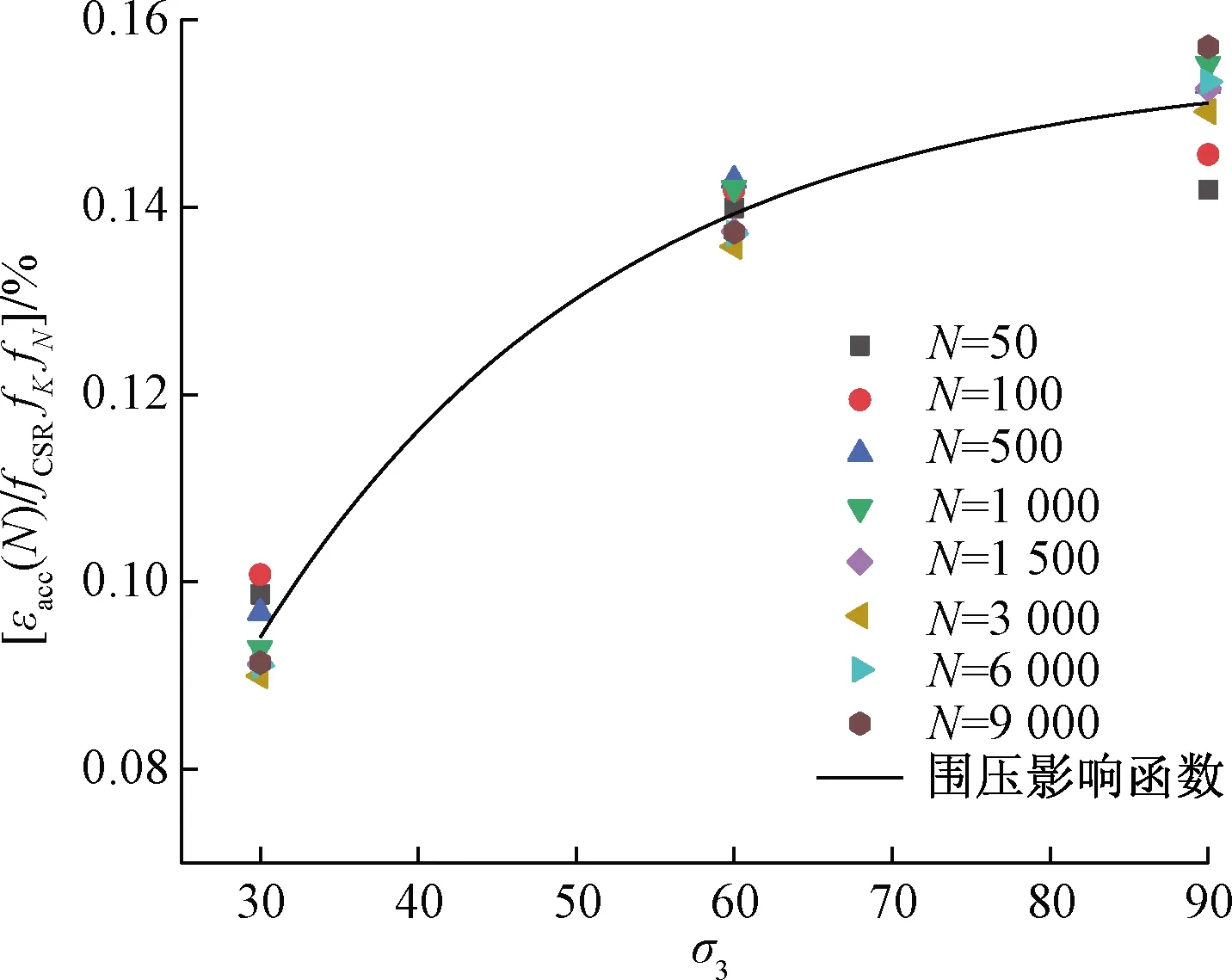
图9 累积应变的围压影响系数

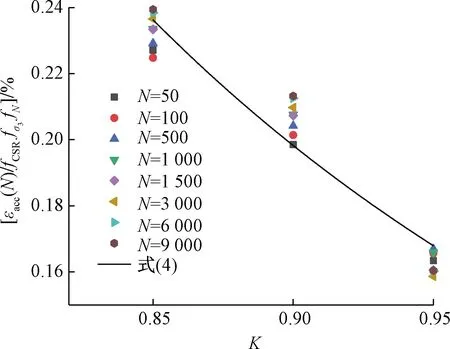
图10 累积应变的压实度影响系数

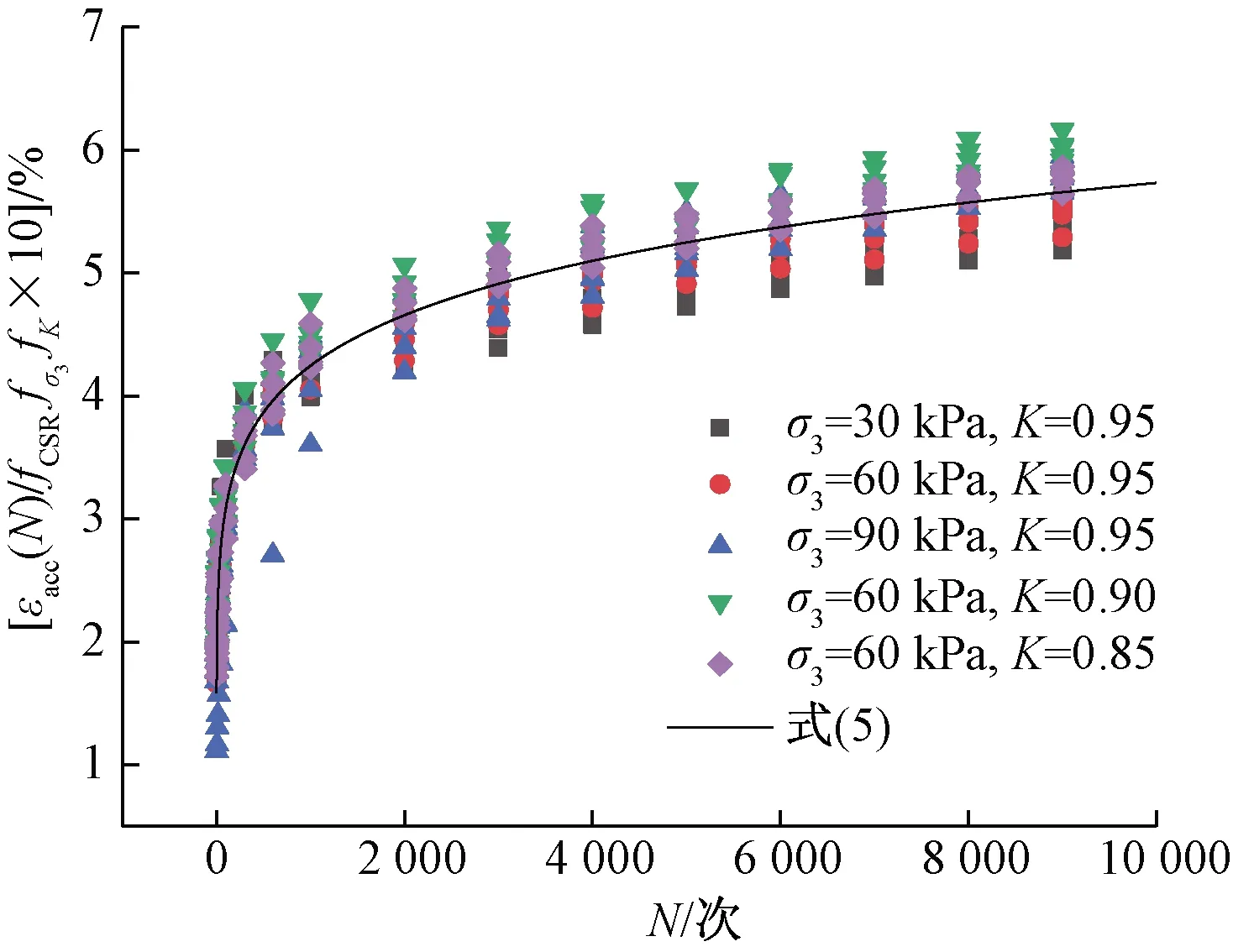
图11 归一化累积应变与荷载振动次数的关系

3.2 累积应变模型的验证

下面为了验证本文提出的预测模型的可靠性，对试验数据和采用式(1)计算的结果进行了比较。从图12可以看到，式(1)虽然不能十分完好地拟合试验数据，但也很好地反映了累积应变的变化趋势，在实测曲线附近出现些许的波动，误差尚可接受。

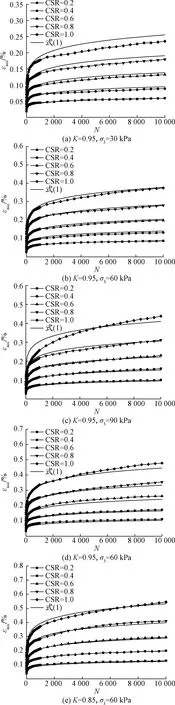
图12 试验值与预测值对比

4 结论

针对铁路路基填料中常见的粗粒土填料，利用GDS动三轴仪开展了一系列动三轴试验，对比分析了不同动应力比、不同围压以及不同压实度对粗粒土填料累积应变发展规律的影响，建立了由动应力比、围压、压实度控制的粗粒土填料累积应变预测模型。得到以下几个结论。

(1)施加循环荷载后，初期累积应变的发展速度非常快，当达到1 000振次后，累积应变大约为总累积应变的75%，而后累积应变的发展速度又逐渐降低，最终累积应变会趋于稳定。

(2)动应力比是影响累积应变发展规律的一大因素，所施加的动应力比越大，试样的累积应变和应变发展速率就越大。在压实度为0.95、围压为60 kPa的条件下，应力比为1.0时的累积应变是应力比为0.2时的4.29倍。

(3)围压是影响累积应变发展规律的另一因素，不同的围压表示不同的深度处的路基土体，在相同应力比条件下，围压越大，累积应变就越大。在本试验中当围压分别为30、60、90 kPa时，在10 000次荷载作用下的累积应变分别为0.132%、0.200%、0.230%，涨幅分别为1.52倍和1.15倍。

(4)压实度也是影响累积应变发展规律的一个因素，在其他相同条件下，压实度为0.85、0.9、0.95的土样在10 000次的荷载振动作用下，累积应变分别为0.295%、0.263%、0.200%，压实度为0.9的试样比压实度为0.85的试样累积应变减少了大约10.85%，而压实度为0.95的试样比压实度为0.9的试样累积应变减少了23.95%。

(5)本文中建立的由应力比、围压、压实度控制的累积应变预测模型能够较好地反映粗粒土填料稳定型累积应变发展规律。