长江浦口段江滩复绿对河道行洪能力的影响

王玲玲，姜兆宇，韩建军，胡礼涵

(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098; 2.河海大学水利水电学院，江苏 南京 210098)

长江浦口段江滩复绿工程位于南京市浦口区滨江岸线北岸13.9 km江滩上，该江段滩浅槽深，江心洲发育，北岸平均滩宽约350 m，南岸平均滩宽约150 m，平均槽宽2 500 m，这类滩槽宽度比小于1的河道称为窄滩复式河道[1]。江滩上原有的39家船厂拆除后，环境杂乱、场地硬质化高，厂址与江滩上零星的原生植被相间分布，阻断了连续性滨水绿道。为改善沿岸生态环境、提升江滩景观性，对原有船厂遗址区域进行场地平整，并对江滩进行人工复绿。而江滩灌木、乔木的种植，将减小复式河道的过流面积，增加水流阻力[2-5]。长江来水大于平滩流量时，洲滩开发利用工程会引起整个河道水位的明显抬高[6]，对行洪产生不利影响。但是这类复绿工程的影响程度时空分布不均，规律难以量化，影响因素众多[7-9]。黄本胜等[10]研究发现珠江三角洲复式河道河滩植被带进口处水位显著壅高，以此建立经验公式，用于估算上游水位最大壅高值与滩地和全断面过水面积之比的关系。石月珍[11]通过对称双边滩地的复式河道物理模拟试验，研究了不同水深和滩地种树密度条件下滩槽流量分配比的变化。王忖[12]通过水槽试验研究了有刚性植被的复式断面河道水流，发现滩地种树密度及树木排列方式对河道水位变幅和流速差有明显影响。任杰等[13]以嫩江干流东阳堤段为例，建立二维水动力模型定量研究了滩地种植防浪林对复式河道行洪的影响，识别了影响行洪的2个关键因素：滩地水深和林带宽度。前人的研究大多集中在采用概化模型研究滩地宽度、滩地水深、种树密度和树木排列形式等单变量对河道行洪能力的影响，对于天然复杂河道、不同来流量与特定复绿方式耦合作用下河道行洪影响的研究较少。本文以长江浦口段江滩复绿工程为研究对象，基于MIKE21 FM建立工程区段二维水动力模型，研究复绿工程对长江高水行洪的影响，以期能为天然复杂形态河道岸滩整治工程的规划利用提供参考。

1 江滩复绿工程概况

长江浦口段江滩复绿工程范围为驷马山河—石碛河之间长约13.7 km的南京长江段北岸滩地，如图1所示。该段平均河宽约3 km，最大水深约50 m，水平尺度远大于垂向水深。北岸平均滩地宽约350 m，高程范围3.5～10.0 m；南岸平均滩地宽约150 m，高程范围3.0～9.0 m。河槽平均宽约2 500 m，高程范围-10.0～-35.0 m。工程江段洲滩发育，分布有新济洲、新潜洲等江心洲，高程范围3.0～8.5 m。根据水位消落和土质情况，筛选耐旱、耐淹、抗冲刷且能固土的植物，沿湿度梯度方向草-灌-乔阶梯状配置近自然植物群落。考虑到长江水位变化，高程8.0 m以下以地被植物固土为主，高程8.0 m以上以组团形式点缀栽植乔灌木。其中高程8.5 m以下为水生苔草、花叶芦竹、再力花等，高程8.5 m以上以水生鸢尾、黄菖蒲为主，高程10.0 m以上少量大花萱草、酢浆草、木芙蓉等。

图1 研究区域范围Fig.1 Scope of research area

2 研究方法

2.1 控制方程

二维水深平均数学模型控制方程由连续方程和动量方程组成：

(1)

(2)

(3)

式中：ζ——水面高程；p、q——x、y方向通量密度；d——时变水深；h——水深；g——重力加速度；C——谢才阻力；ρw——水的密度；f——风摩擦系数；v、vx、vy——风速及其在x、y方向上的分量；pa——大气压力；x、y——空间坐标；t——时间；τxx、τxy、τyy——有效剪应力的分量。

2.2 数值方法

空间离散方法采用有限体积法，控制体形状为三角形及四边形。控制方程离散时，速度分量位于单元中心，跨边界通量垂直于单元边。时间积分采用二阶Runge-Kutta方法，其通式为

(4)

时间积分公式为

(5)

式中：U——通用物理量；G——U的连续函数；Δt——时间步长；i、i+1/2——第i时刻、中间时刻。

3 复绿工程水动力模型构建

3.1 区域网格与边界条件

模型上边界位于慈湖河口上游1.90 km，下边界位于南京水文站下游1.85 km，区域总长约30.0 km。采用非结构化三角网进行计算区域剖分，网格最小角度为25°。网格单元总数为9 770，节点总数为6 147，兼顾计算效率和稳定性选取时间步长初值为60 s。

地形资料采用2013年实测地形，复绿工程所在的北岸局部采用2019年实测地形进行修正。根据《长江流域综合规划》确定长江中下游防洪标准：荆江以下河段以防御1954 年洪水为目标。大通站1954年8月1日最大洪峰流量为9.26万m3/s；水位取南京设计洪水位10.6 m，考虑洪水比降后，插补得下游边界水位为10.87 m。

3.2 糙率取值

3.2.1 复绿工程前糙率率定

率定依据为2008年7月30日0时至8月4日0时计算区域的一次测流过程，其上下游边界均为实测的水位过程。以 CS1、CS2水文测验断面(图1)的实测平均水位过程进行滩槽糙率率定，计算与实测水位对比如图2所示(图中时间为距离2008年7月30日0时的时间)，CS1、CS2断面纳什效率系数[14]分别为0.958和0.997，表明计算结果具有较高精度。率定得河槽糙率为0.021，滩地糙率为0.026。

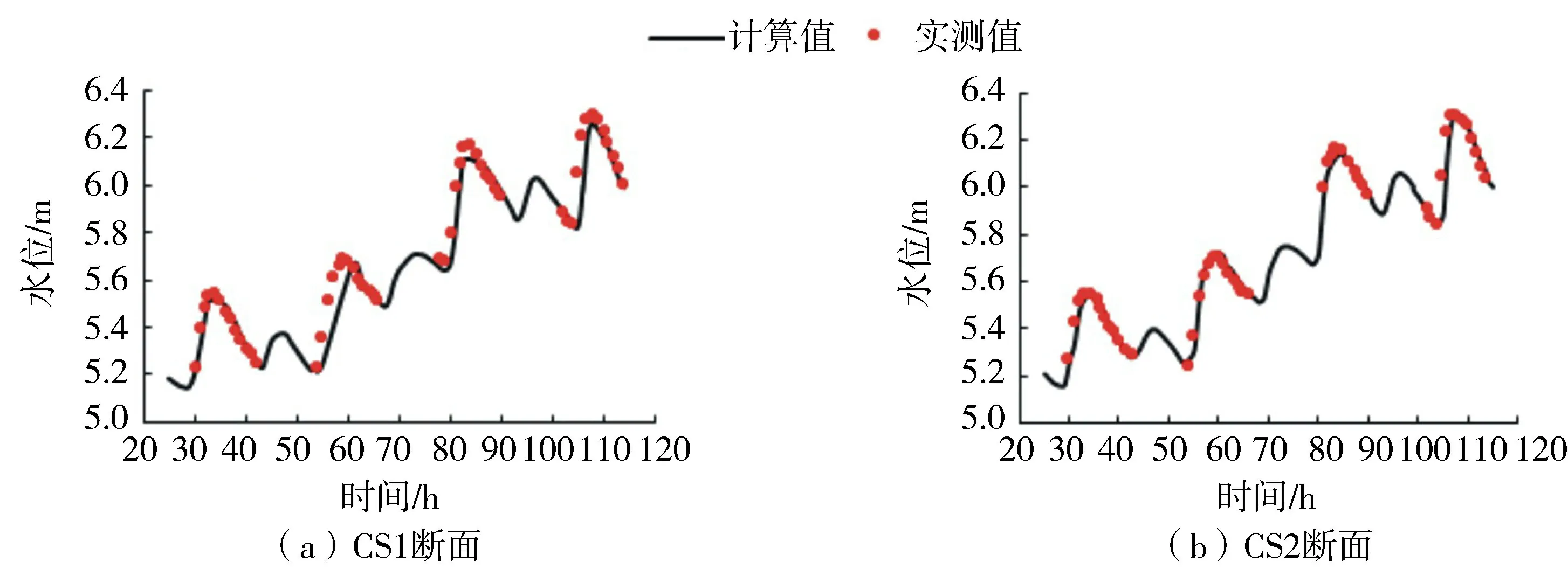
图2 2008年水位计算值与实测值对比Fig.2 Comparison of calculated and measured water levels in 2008

3.2.2 复绿工程后滩地糙率取值

复绿工程后糙率取值依据Moghadam等[15]的糙率计算公式进行计算：

(6)

式中：uc——断面平均流速；hn——正常水深；hv——植被平均高度；hn/hv——植被相对淹没度；A——植被水平投影面积；a——明渠水平投影面积；A/a——植被相对密度。

槐文信等[16]基于2009年汉江上黄庄至兴隆段河道汛期的水文、地形资料，利用式(6)所得糙率计算了某断面的水位、流量过程，计算结果与实测结果吻合良好，证明了式(6)在天然复式河道糙率计算中具有良好的精度和可靠性。

依据复绿工程方案植被分布形状和连续性，将北岸滩地概化为3段(图3)。第一段滩地形状近似矩形，植被分布连续紧凑；第二段滩地形状复杂，植被集中在3块不连续的小区域；第三段滩地形状近似狭长矩形，植被随滩地呈连续的狭长带状分布。将北岸滩地区域视为含植被明渠过水床面，利用式(6)计算各段糙率，其中hn取各段滩地上的平均水深，各段水位由设计洪水位插补得到，3段滩地代表断面平均水位分别为11.6 m、11.4 m和11.23 m；以植被面积为权重，加权计算出各段hv；A=Sc(S为工程规划植被面积，c为植被密度)，根据Moghadam的试验结果，糙率对c的变化不敏感，可取c=0.5；a为各段滩地总水平投影面积；uc采用试算法得到，即初选各段uc值，利用式(6)计算糙率后用数学模型计算新的流速均值，修正uc值重新计算糙率，直到收敛。由此计算得工程后的北岸滩地第一、二、三段糙率分别为0.028、0.027和0.029，参考第3.2.1节率定结果，河槽糙率和南岸滩地糙率分别为0.021和0.026。

图3 北岸滩地植被分布Fig.3 Distribution of vegetation on north floodplains

4 计算结果分析

4.1 江滩复绿对水面线影响

由图4可知，主槽在植被带上游出现了约1 cm的壅高，植被带区域壅高值沿程回落，植被带下游出现较小的水位跌落，水位壅高迅速衰减为零。北岸滩地水面线壅高特征与主槽基本相似，不同点在于植被带进口附近壅高值出现了约1 cm的急剧抬升并达到峰值，最大壅高约为0.02 m，壅高值波动较主槽更剧烈。表明江滩复绿将使滩地水流不稳，能量损失现象明显，对滩地水位的影响远大于主槽水位。

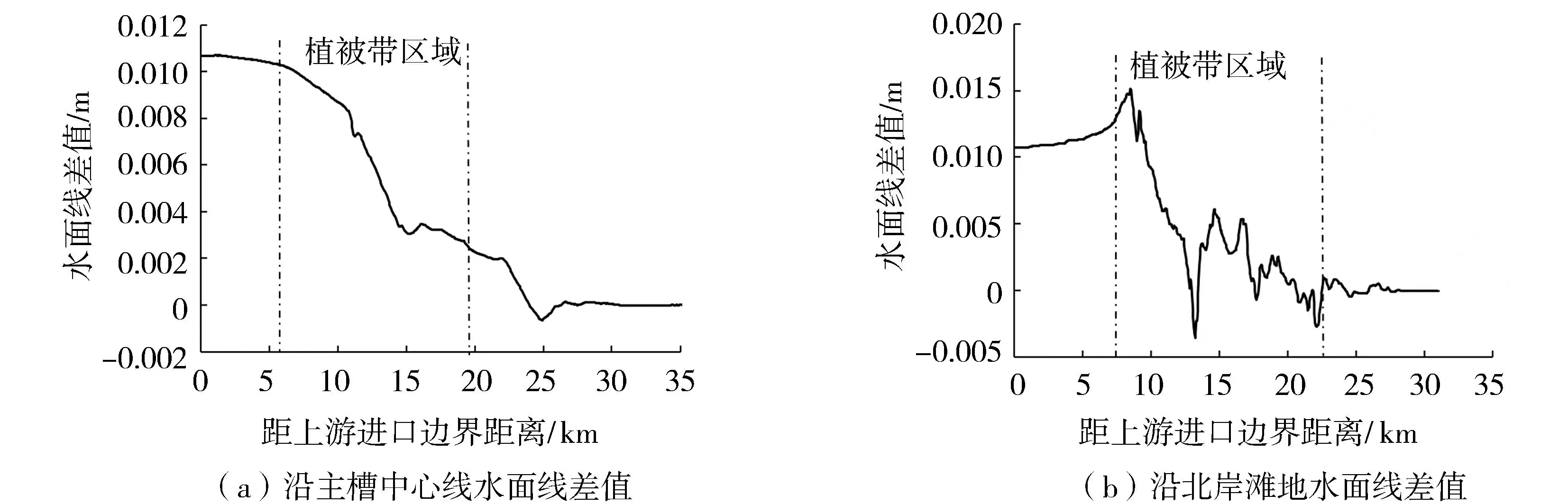
图4 复绿工程后沿程水面线变化Fig.4 Changes of water surface line along river after vegetation construction

4.2 江滩复绿对流速分布影响

由图5(图中红线描绘出滩地轮廓)可知，河道北岸滩地流速明显降低，植被带区域流速降低尤其明显，局部降低0.02～0.06 m/s。主槽及南岸滩地流速升高0～0.2 m/s。表明受植被带阻力作用，北岸滩地过流能力降低，上游水流偏向右侧主槽，改变了滩槽的流量比。滩槽之间存在较大的流速差，形成较大的流速梯度，增强了水体对滩地的冲刷作用。交界面会产生由大量旋涡组成的“涡街”，使滩、槽水流相互作用加强，产生动量和能量交换[17]，也使水流能量耗散加强。

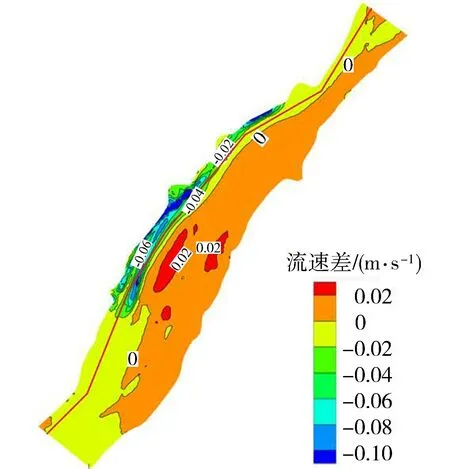
图5 复绿工程后流速变化Fig.5 Velocity change after vegetation construction

4.3 不同流量对水位壅高影响

1946—2006年大通站洪季最小流量为2.78万m3/s[18]，1954年8月1日最大洪峰流量为9.26万m3/s。为研究不同流量Q对江滩复绿引起的水位壅高影响，在3万～9.5万m3/s之间每隔5 000 m3/s取一流量作为上游边界条件。李国芳等[19]选取1983—1987年高水期大通站逐月最大流量和相应的下关站逐月最大水位，做线性回归并点绘出水位-流量关系曲线,依据此曲线，可确定各流量对应的水位值作为下游边界条件。

由图6可知，不同流量下水位变化分布规律基本相似：植被带上游水位壅高较大，峰值区域出现在江滩植被带进口附近，中下游水位变化小。流量由3万m3/s增大到4万m3/s时，水位壅高峰值区域范围增大，上游平均壅高增大。流量由4万m3/s增大到8万m3/s时则相反，水位壅高峰值区域收缩明显，上游平均壅高减小。

图6 复绿工程后不同流量下水位变化分布Fig.6 Distribution of water level change corresponding to different discharge after vegetation construction

上游最大水位壅高和上游断面平均壅高与河床上游平均水深之比分别记为Zm/H、Za/H，上游流量与9.26万m3/s之比记为Q/Q0，点绘Zm/H、Za/H与Q/Q0关系曲线如图7所示。由图7可知，Q/Q0由0.32增加到1.03，即流量由3万m3/s增加到9.5万m3/s时，Zm和Za都呈先增加后减小的趋势。Zm的变化幅度较Za的变化幅度更明显，且减小趋势的出现早于Za，说明上游Zm对流量变化更敏感。

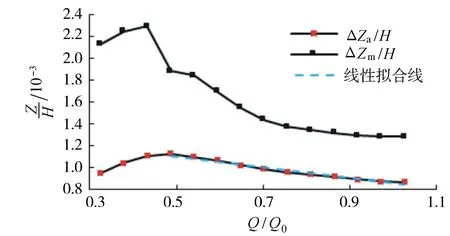
图7 无量纲水位壅高与无量纲流量关系曲线Fig.7 Relationship curve between dimensionless banked up water level and dimensionless discharge

黄本胜等[1]通过水槽试验模拟河滩种树对窄滩复式河道行洪的影响，发现上游水位壅高与植被带宽度和漫滩水深成正相关。植被带宽度与漫滩水深的乘积即为植被带的阻水面积。研究范围江滩平滩流量约为3万～3.5万m3/s，滩地植被带平均高度为1.4 m，其被完全淹没的流量大约为5.5万m3/s，而Za的减小趋势在4.5万m3/s流量条件下就已经出现。可以认为在水流未完全淹没植被带时，流量的增大对上游水位壅高同时存在两种相反的作用：一是所引起的植被带阻水面积增大对上游水位壅高的增大作用，二是整体水位抬升削减了滩面局部阻力造成的上游水位壅高。当3万m3/s

流量4.5万～9.5万m3/s区间ΔZa/H与Q/Q0存在较好的线性关系，回归方程为

(7)

根据式(7)可以预测淹没条件下植被带上游断面平均壅高。1922—2002年大通站最大洪峰记录资料显示，大通站在大洪水年份洪峰流量为6.5万～9.26万m3/s[20]，研究区域河床上游平均水深介于5.5～11.5 m范围，可估算此时江滩植被引起的上游断面平均壅高介于0.5～1 cm范围。

5 结 论

a.江滩植被对长江浦口段窄滩复式河道行洪能力有一定影响，具体表现为：植被带上游水位壅高，滩地流速减小，主槽流速增大。

b.确定了复绿工程附近江段滩面临界水深值为1.3 m。滩面水深小于或大于临界水深时，流量引起的上游壅高变化趋势截然相反。临界水深的确定对长江浦口段岸滩整治工程规划和行洪水位壅高预测具有重要意义。

c.得到了研究范围河段4.5万～9.5万m3/s区间无量纲上游断面平均壅高与无量纲流量的线性拟合方程，预测了大洪水年份江滩植被引起的上游断面平均壅高介于0.5～1 cm范围。