基于马尔科夫和蒙特卡洛的战时航材需求预测

吴捷，郭峰，张素琴

（海军航空大学青岛校区，青岛 266041）

引言

在现代高科技战争中，航空兵是决定战争胜负的重要因素之一。作战飞机对航材的依赖性极大，因此做好航材需求预测工作具有重要的军事和经济意义。现代战争具有很强的变异性、复杂性以及多样性，加之作战飞机的频繁使用及战场环境恶劣，飞机的战斗损伤不可避免，战时航材消耗较平时会呈现许多不同的特点和规律。但由于战时样本量极少，很难用一般的预测方法进行需求预测，并且预测精度很低，这就给战时航材保障人员在进行航材保障时带来很大困难。战时航材需求预测是一个十分复杂的过程，构建一个精确的模型对航材需求数量进行准确预测极其困难，战争不会重复发生，也不可能等到下一场战争爆发再用其来检验预测的准确性。鉴于此，笔者以MATLAB为仿真平台，结合蒙特卡洛方法以及马尔科夫方法对战时航材需求进行计算机仿真模拟，以期预测战时作战飞机航材需求变化趋势，为决策部门制定航材供应数量提供一定的参考依据。

1 马尔可夫模型

1.1 马尔可夫预测法原理

马尔可夫预测法是对事件下一时刻各种状态发生的概率进行预测的方法，通过对当前状态的分析来预测其未来各个阶段状态变化。假设一个事件所有可能的状态分别记为E1，E2，…，En且该系统每次只能处于其中的一种状态中，此事件下一步的状态只有在时间流转到固定且顺序排列的时刻t上才会发生变化。可以通过一系列的随机状态参数Xn（n=1，2，…）来描述，其中当Xn=k，表示在t=n时刻，事件所处的状态为

在事件各部分相互作用动态变化的过程中，从t时刻的状态启动，经过k个时刻变化到下一状态（可能为相同状态也可能不同）的概率，称作k步状态转移概率。经过Ei变为Ej的状态转移概率简记为：

假定事件所有可能存在的状态共有n个，为E1，E2，…，En。把Pij作为矩阵的第i行第j列，则n个状态（j=1，2，3，…，n）共有n行，则由状态Ei转变为状态Ei的状态转移概率矩阵为：

1.2 战时航材需求的马尔科夫性分析

在战争爆发的时候，存在相当数量的航材，其每个月的消耗数量是一个很小的正整数（其数量一般不超过5个），此种作战所需航材的需求量是一个随机的、不确定的量，并在战争持续时间内表现出随机波动的特点。时间序列预测法及灰色系统预测法均不能有效地预测其需求量。过去的战争数据和平时的训练数据只能作为一个参考，战争的演变速度很快，对战时物资的需求日新月异，过去的数据信息对现在价值不大，因此我们可以假设此类航材未来的需求量的情况与“过去”的情况是无关的，只与当前状态有关，即该类航材需求量具有马尔可夫性，马尔科夫性也称为无后效性[3]。事物第N次出现的状态只与其第N-1次的状态有关，它与再往前的历史状态无关[4]。

1.3 马尔科夫模型分布研究

由该类航材马尔可夫性可知，过程在时刻s处于状态i条件下，在随后的t个单位时间中过程仍不离开状态i的概率，是它处于i至少t个单位的无条件概率[5-7]。若记hi为过程在转移到另一个状态之前停留在状态i的时间，则对一切s，t≥0有：

由此可见，随机变量hi具有无记忆性，对于一条马尔可夫链，由于战争不会无限制地持续下去，我们仅截取马尔可夫链中符合战争持续时间的一部分，每当其演变到状态i，在事件变化到下一个状态的时间内，马尔科夫模型服从具有特定参数的指数分布[8，9]。

若已经知道当前月份的需求量，便可以利用前述矩阵P来计算未来有限月份内航材需求量的各种状态的发生概率。对未来3个月（即假定战争持续时间为三个月）的航材需求量各种状态的概率累加就能够得出战争持续时间内航材需求量的概率分布情况。

1.4 马尔科夫模型预测流程

第一步以时间t划分阶段，航材在某一时间段内的消耗情况作为状态量，该种低需求航材的月需求量为X，则该种低需求航材在状态t1，t2，…，tn的取值分别为x1，x2，…，xn，该种航材需求数据中最大值记为Xmax，最小值记为Xmin，航材需求量为整数则，该种航材共有Xmax-Xmin+1种状态。

第二步，根据航材样本实际情况，用频率近似替代概率，设Yi为处于状态Ei的样本数；Yij（k）为状态Ei，经过k步转移到状态Ej的数据个数，用Pij（k）表示k步转移概率，如下所示：

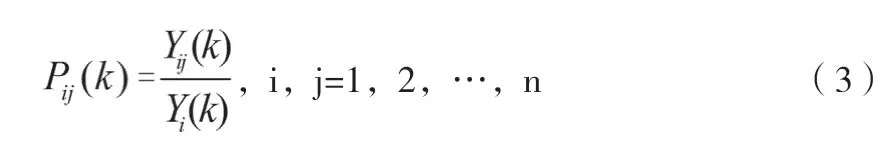
则相应的k步状态转移概率矩阵P（k）就可以表示为：

第三步，求解任意阶段状态概率向量，当前时间航材需求个数即为当前状态，并通过之前的战备训练记录数据计算出转移概率矩阵，就能够预测出当前时间往后k步航材数量所处于的各种状态，用C（t）表示战争爆发后第t个月的航材各需求量出现的可能性矩阵，预测公式如下所示：

2 蒙特卡罗法

2.1 蒙特卡罗算法原理

蒙特卡罗算法是一种以大数定律为基础，通过大量试验来模拟随机现象的方法，当模拟次数达到一定数量后，模拟数据的特征就越接近现实情况。蒙特卡罗算法需要根据数据规律，把确定性问题与某个概率模型相联系，用模拟试验所得统计值代替无法精确计算的理论值，从而解决复杂问题[10-12]。

2.2 蒙特卡罗仿真基本框架

第一步，建立数据与目标值的关系，构造概率模型，对于本来不是随机问题的确定性问题，需要人为地构造一个概率分布模型。

第二步，实现从构造概率分布的抽样。为实现仿真，必须进行随机变量的抽样，进而得到符合构造的概率分布的随机序列，即样本值。

第三步，建立各种统计量的估计。作为问题的解，可能是概率或期望。对于前者则用频率代替，对于后者用样本算术平均值代替，从而近似求解出预测值。

2.3 基于蒙特卡罗的航材状态概率随机模拟

首先分析战时低需求航材的马尔科夫性，通过MATLAB内置的unifrnd (a，b，m，n)函数，产生m×n个在[a，b]上服从均匀分布的伪随机数，将产生的结果与马尔科夫模型产生的航材各需求量状态概率进行拟合。为了使蒙特卡罗模拟效果更具可靠性，更加符合实际，使用MATLAB内置exprnd（MU，m，n）函数，先根据战前积累的航材历史数据，计算其统计平均值MU，接着计算机生成m×n个均值为MU的服从指数分布的随机数序列。在剔除波动较大的数据序列后，将同一时间点的随机数与真实数据相减，将其中方差最小的一组随机模拟数据作为计算机模拟的战时航材需求序列，与原始数据可视化对比，进行误差分析。具体步骤如下：

1）首先在MATLAB中以矩阵的形式输入航材需求历史数据，编写程序找出其中最大值和最小值，计算出需求量可能存在的状态。令t=0，记录所需要预测的未来C个月的个数C。

2）统计每种状态数量，以及由该种状态下一步转移状态数量，计算出第1步状态转移概率矩，P（1），并以此类推计算出第2、3、…、C步状态转移矩阵。

3）根据最后一个状态的样本值，计算出未来C个月各个状态对应需求量的概率预测值。

4）令t=t+1，使用unifrnd函数生成C个在[0，1]上服从均匀分布的随机数。

5）将概率拟合转换为具体的航材需求数量，若生成的随机数大于0且小于等于变为第一种状态的概率，这时该航材的需求量为0，若生成的随机数大于变为第一种状态的概率且小于等于变为前两种状态的概率之和，则该航材的需求量为1，以此类推求得第2、3、…、C个月的该航材需求量。

6）将这C个月的航材需求量求和，分别统计其中0、1、…、C×Xmax出现次数。

7）当t小于规定的模拟次数M时，流程回到步骤2），当t大于等于规定的模拟次数M时仿真停止，将步骤6）中各需求量出现的个数除以总仿真次数M，输出结果并绘制图形。

8）使用exprnd函数产生随机航材需求数量序列，用该数据组与通过MATLAB产生的服从指数分布的航材需求数据组进行逐项对比，检验模型预测效果。

马尔科夫模型蒙特卡罗方法仿真流程如图1所示。

图1 马尔科夫模型蒙特卡罗方法仿真流程图

3 实例分析

已知某型飞机装备实力与飞行任务量的变动不大，飞机上装载的某型蓄压器需求数据样本统计时限为2019年4月~2020年7月，如表1所示。

由表1可知数据中最大值为2，最小值为0，该型蓄压器需求数量共有三种状态，对时间序列进行统计，用频率近似地表示一步转移概率，由以上数据知，需求数为0的月份有2、6、9、10、12、14、15共7个，由需求数为0经过一步转移到需求数0的数量为2，则

表1 需求数据样本

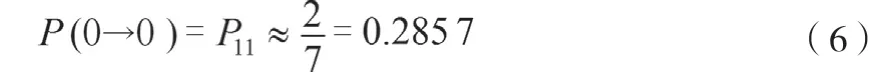
同理可以计算出一步概率转移矩阵P（1）：

以此类推，利用计算MATLAB计算出P（2）、P（3）如下：

根据需求时间序列可知当前此航材该月需求量为1，根据概率转移矩阵P（1）、P（2）、P（3）可以计算出未来第1、2、3个月的航材需求状态概率分布，利用MATLAB模拟1×104次，统计战争持续时间内航材需求量为0的状态出现次数为326，航材需求量为1的状态出现次数为591，以此类推，除以仿真次数，得到航材总需求的累加概率，结果如表2所示。

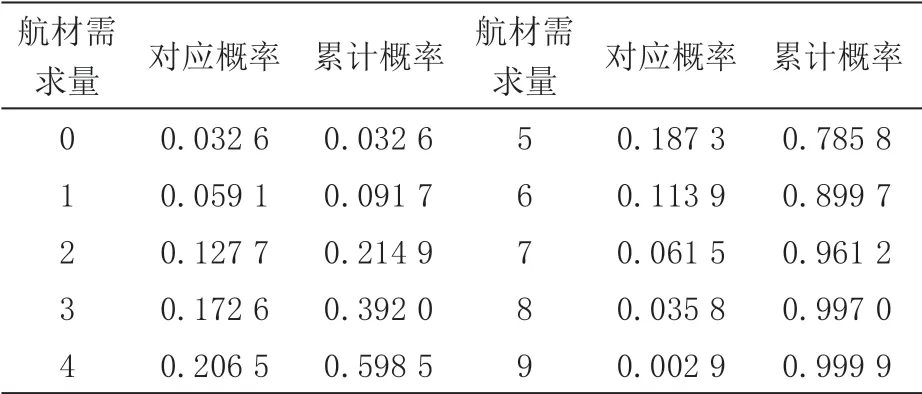
表2 状态概率对应表

根据航材需求量和累计概率的对应关系，可以绘制出在战斗持续的三个月时间内该航材的数量所对应的战时航材需求的满足率，如图2所示，由图可知，该航材在战时三个月内需求量为7个的时候，对应的需求满足率达到了96 %以上，我们不必追求百分之百的满足率而在战前储备10个该型蓄压器，为了很小的满足率的提高，需要投入巨大的人力成本和经济成本，虽然相较于经济成本来说，军事效益是摆在第一位的，但是我们可以在战争开始的时候先储备7个蓄压器，再依据战场态势的变化灵活进行补充。

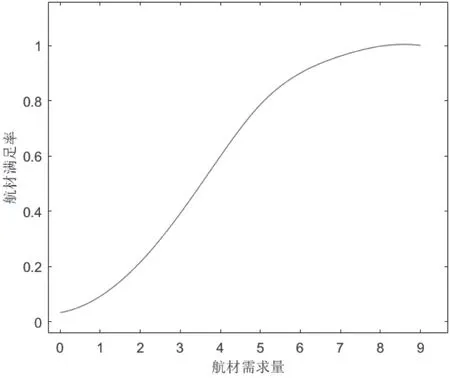
图2 航材个数与航材满足率的关系

4 误差分析

基于马尔科夫模型和蒙特卡洛法的战时航材需求预测，由于缺少真实的战场需求数据作为误差分析的依据，给误差分析增添了许多的困难。笔者为了检验模拟预测的可靠程度，根据现有蓄压器需求数据，计算出其均值为0.75，其方差为0.60。使用MATLAB内置exprnd函数，生成16×10 000个均值为0.75的服从指数分布的随机数。将真实数据与仿真产生数据方差最小的序列作为随机模拟蓄压器需求量结果，绘制图形如图3所示。

图3 原始数据与模拟数据对比图

计算机模拟出的序列整体数据波动变小，大部分最值点在时间趋势变化上与原需求序列拟合较好。依据指数分布所模拟出来的均值、方差等指标与原始数据相差不是很大，说明该种蓄压器需求量能较好的服从指数分布。根据新的蓄压器需求序列模拟出未来第1、2、3个月的需求量分别为1.691 0、2.258 7、0.934 7，未来三个月的蓄压器总需求量为4.884 4，可以得知在战争开始前储备好的7个蓄压器较为合理，能够大概率的保证战时该型蓄压器的供应。如果战争的持续时间超过三个月，可以继续使用转移概率矩阵进行需求预测，但是会随着预测时间的延长，导致转移概率矩阵变化增大，从而导致误差增大，后续还需要进行误差的修正。马尔科夫模型和蒙特卡洛结合的预测方法整体模拟效果较好，虽然存在一些误差，但是大体上的预测结果还是较为可靠的。

5 结语

传统的战时航材需求预测模式为了保证战时航材供应充足，往往会将所需航材大量储备起来，从而造成航材积压，消耗大量的资源。本文通过对马尔科夫模型和蒙特卡罗仿真研究，表明了其可以为战时航材需求量的决策提供一定参考，并以一个简单的实例进一步说明了其在战时航材需求预测方面的应用，最后通过误差分析，对有限的历史数据进行仿真处理，以检验高预测的可靠性。同时，因为该预测方法简单实用，只需输入有关数据，就可以通过计算机软件批量处理，且具有一定的可信度，所以还可以推广到其它相似领域的需求预测。