复合材料压力容器的可靠性优化设计

林 峰 冯明扬

（1.杨凌职业技术学院机电工程学院；2.中国电子科技集团公司第三十八研究所）

复合材料由于具有突出的优点，在各领域得到了广泛应用［1］。但是，由于复合材料组分的复杂性，导致其本构参数、外部载荷等多种参数都具有诸多的不确定性，对于不确定性问题，通常考虑的是随机性问题［2］。 随机分析的关键在于确定每个随机参数的概率密度函数，因此需要充足的概率统计信息。 目前，研究学者们对结构随机可靠性方法进行了诸多研究［3～7］，而对复合材料压力容器结构可靠性设计的研究却很少。 为此，笔者对复合材料压力容器进行可靠性优化设计，为复合材料压力容器的可靠性预测与设计提供一种简便可行的方法。

1 压力容器模型及可靠性分析依据

1.1 压力容器模型

采用ANSYS 软件中的SHELL181 单元类型建立压力容器壳体结构模型，如图1 所示。 压力容器结构采用T800 碳纤维，正交铺设，共8 层，层厚1mm。 球形封头直径为350mm，筒体段是外径为350mm 的圆柱，圆柱段长500mm，设计内压力载荷为3.2MPa。 由于压力容器模型是对称的，为了减少计算时间， 取有限元模型的1/2 进行分析计算，同时对球形封头顶端施加固定约束。

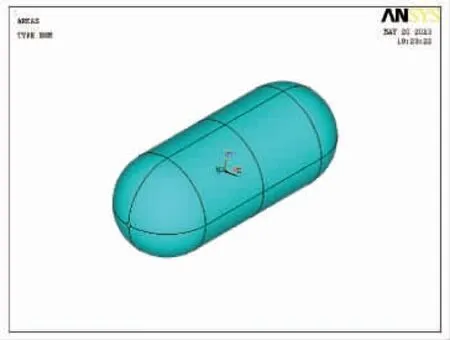
图1 复合材料压力容器壳体结构模型

考虑到后续Monte-Carlo 模拟需要多次迭代，为了提升计算效率，需要合理选择有限元网格数量。 通过对最大环向应变值的比较，最终选用2 000 个网格对有限元模型进行网格划分， 此结果比更多数量网格的有限元模型更为保守，且不会造成结构失效。

1.2 可靠性分析依据

如图2 所示，环向位移主要发生在直径不变的直筒段和直径开始变化的球形封头与直筒段结合部位，最大环向位移发生在曲率半径变化的部位，所以该部位是最容易发生失效的。分析图3可知， 应力与应变同图2b 环向位移的变化趋势一致，为此可选环向最大总应变（US）作为可靠性分析依据， 只要计算该值小于许用值的概率，就可计算出可靠度。

图2 形变和位移云图

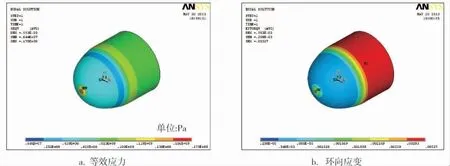
图3 应力与应变云图

2 基于ANSYS 的压力容器可靠性分析

Monte-Carlo（MC）方法是一种基于统计学原理来解决随机问题的数学方法，是用来验证随机可靠性分析结果准确性的唯一方法。

在工程实际中，考虑到结构所承受的外载及其自身结构参数、本构特征参数（包括弹性模量Ex、Ey和Ez，剪 切 模 量Gxy、Gxz和Gyz，单 层 纤 维 厚度h，内压力载荷p 等）的随机性，设定这些参数均服从正态分布，详见表1［8］。

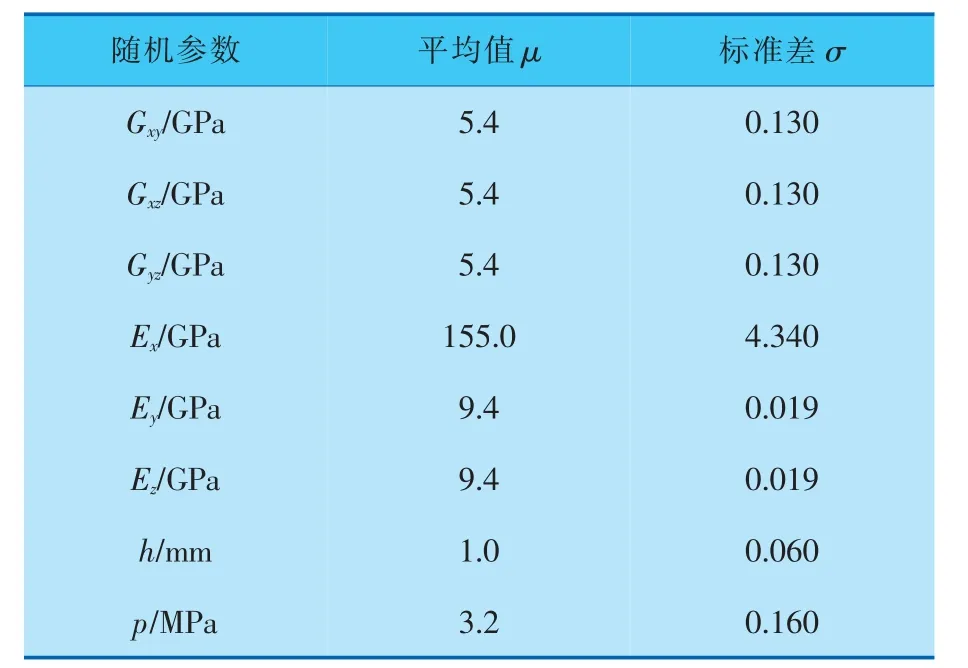
表1 随机参数的正态分布

极限状态函数为：

其中，当Z（X）＜0 时为失效状态，故该结构的可靠度即为Z（X）＞0 的概率；es为复合材料层合板在设计载荷下的许用拉伸应变，其值为0.007 6；emax为环向最大总应变（US）。

以环向最大总应变（图4）为例，进行5 000次数值模拟计算，蓝色曲线表示MC 迭代不同次数计算出的参数均值，上下两条红色曲线表示置信度为95%时区间的上下界。 由图4 可以看出，在迭代次数达到3 750 次之后环向最大总应变均值基本保持不变，说明此时迭代次数已足够。 因此，为了保证精度、提高计算效率，后续MC 模拟计算采用4 000 次的迭代次数。

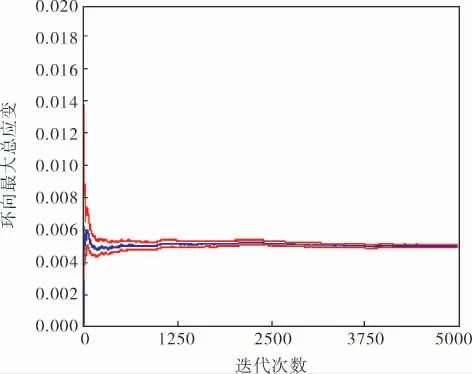
图4 环向最大总应变随MC迭代次数的变化曲线

图5 是环向最大总应变的概率密度分布直方图，即概率密度函数图像，对它进行积分即可得到图6 所示的概率累积分布函数。 由图6 可以看出，环向最大总应变为0.007 6，对应的概率值是99%，即此时结构的可靠度为99%。

图5 环向最大总应变的概率密度分布直方图

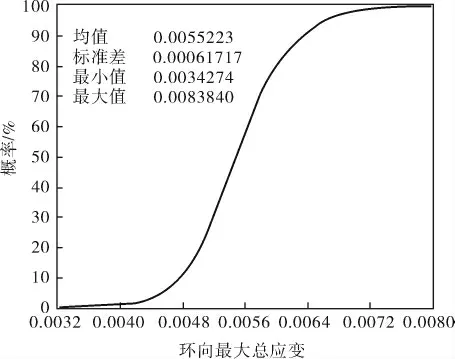
图6 环向最大总应变的可靠度分布

3 基于可靠度的优化设计

优化设计之前有必要先对输入参数进行灵敏度分析，找出对结果影响大的输入参数，同时忽略影响较小的参数，从而提高计算效率。 通常，灵敏度大于2.5%的参数为显著影响因素， 小于2.5%的参数可以忽略。

输入参数的灵敏度分析如图7 所示，可以看出， 输入参数h、p、Ex和Gxy均为显著影响因素，其中h、Ex和Gxy对结果呈负相关性，p 对结果呈正相关性，而其他参数可以忽略。

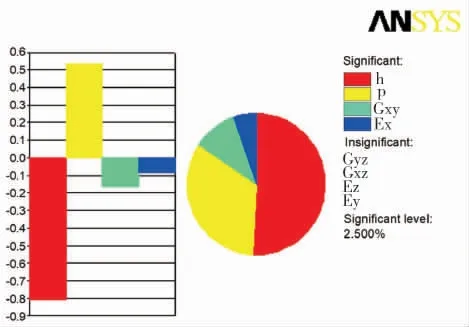
图7 输入参数的灵敏度分析

优化设计时， 设Ex和Gxy是设计变量（DV），US 和p 是状态变量（SV），h 是目标变量（OBJ）。

内压力载荷p 为3.2MPa，经过10 次迭代，得到优化结果见表2， 将优化结果带入可靠性模型进行验证，得到可靠度为99%。 优化结果中h 为0.804 9mm，小于设计初始的1mm 单层厚度，此时材料力学性能得到了充分发挥， 既节省了材料，又满足了可靠性要求。

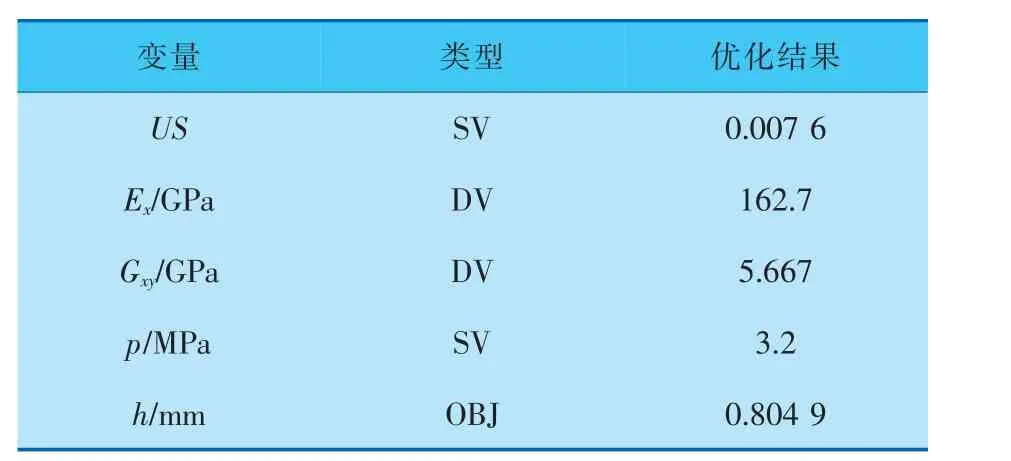
表2 优化结果

4 结束语

笔者针对某航天工程中的复合材料压力容器进行了结构可靠性优化，建立了复合材料压力容器的有限元模型， 基于ANSYS 有限元软件的可靠性分析模块，计算了结构的可靠度，并基于可靠度对该结构进行了优化设计。 结果表明，采用基于可靠度的优化设计，既能满足结构安全要求，又能充分节省材料。