虚拟轨道车辆二系垂向刚度和阻尼对车辆平稳性和可控性的影响分析*

赵昀陇，池茂儒，贾 鹏，张成铭，于忠建，代亮成

（1 西南交通大学 牵引动力国家重点实验室，成都610031；2 中车长春轨道客车股份有限公司，长春130062）

随着现代城市交通的不断发展，交通方式的不断创新，丰富的出行选择极大的降低了人们出行的时间，虚拟轨道车辆不仅能够丰富人们的出行，而且兼顾了轨道列车和汽车乘用车的优点，可以灵活运行在复杂的城市空间。目前，我国湖南已经建成第一列虚拟轨道示范线［1］，在多个其他省市也开始试运行，可见虚拟轨道车辆作为传统轨道交通的有机补充在我国有广阔的市场和前景。然而，由于虚拟轨道车辆包含丰富的电气控制系统和传统机械模块，其运行过程是一个复杂的动力学过程，其平稳性和可控性直接关系到车辆运行的品质和安全，而悬挂参数的取值是否合理又与车辆的平稳性和可控性密切相关，因此，对虚拟轨道车辆的悬挂参数进行研究，掌握悬挂参数对虚拟轨道车辆平稳性和可控性的影响规律，对虚拟轨道车辆的设计是尤为重要的。目前虚拟轨道车辆在国内运用还不成熟，相关学者对此开展了部分研究工作。孙帮成［2］基于全轮差动转向，研究了虚拟轨道车辆的导向循迹控制算法，并搭建了虚拟轨道车辆原理样车；于磊［3］运用无刷直流电机数学模型对虚拟轨道车辆的轮毂电机驱动技术进行了研究，分析了轮毂电机的转矩脉动；曹竞玮［4］建立包含侧向和横摆的线性二自由度车辆操纵模型，并基于循迹效果提取车辆所需的动力学参数，建立虚拟轨道车辆全轮力矩分配方法。但鲜有学者开展虚拟轨道车辆悬挂系统对车辆平稳性和可控性影响的研究。文中根据直接转矩控制理论、胎地耦合理论、车辆系统动力学理论，综合考虑车辆电气和机械系统，基于Simpack和Simulink建立了包含电机驱动系统、循迹控制系统、差动控制系统、多体动力学系统的机电一体化模型，研究二系垂向刚度和阻尼对虚拟轨道车辆平稳性和可控性的影响，为今后的虚拟轨道车辆设计提供理论参考。

1 多体动力学联合仿真模型

1.1 虚拟轨道车辆动力学模型

文中研究的虚拟轨道车辆兼顾轨道列车与公路汽车的特点，其结构较传统铁道列车有所不同，为了实现通过公路上较小的转弯半径曲线和更好地匹配轮毂电机，采用的是每侧双独立轮式结构，单侧一前一后2轮组成一个“走行架”。文中的多体动力学模型采用单车体、每车4个走行架、每个走行架双车轮模式，电动机采用内转子式轮毂电机，将动力装置、传动装置、制动装置整合到轮毂之内，将机械部分简化；车轴与走行架之间装有一系悬挂，车体与走行架装有二系悬挂，考虑需要的自由度，建立多体动力学模型［5］。模型和结构如图1所示。

图1 虚拟轨道车辆模型和结构

1.2 轮胎模型

轮胎模型有多种，文中车轮采用商业上广泛使用的Pacejka模型［6-7］，该模型可统一表示为式（1）～式（3）：

式中：Y（x）为轮胎纵向力、侧向力或回正力矩，x为考虑水平偏移因子时的自变量；y（x）为不考虑垂直偏移因子的纵向力、侧向力或回正力矩；X为纵向滑动率或者侧偏角；D为峰值因子；C为形状因子；E为曲率因子；Sv为垂直偏移因子；Sh为水平偏移因子。轮胎力元输出如图2所示。

图2 轮胎力元的输出

1.3 路面重构

路面重构即路面不平度的重构。公路路面一般在频域上采用功率谱形式来给出统计特性，将其分为A～H共8级，见表1。其分类参数Gq（n0）为参考空间频率下得到的路面功率谱密度值，其公式为式（4）［8］：

表1 路面不平度分类标准

式中：n为空间频率，单位为m-1，它是波长的倒数，表示每米长度中包含几个波长，n为参考空间频率；Gq（n0）为参考空间频率下得到路面功率谱密度值，称为路面不平度系数；W为频率指数，为双对数坐标斜线的斜率，它决定路面功率谱密度的频率结构。

采用谐波叠加法重构A级路面，Gq（n0）中n0取0.1 m-1，n从0.011 m-1到2.83 m-1取值。

f为时间频率，其对于给定的车速v，根据空间频率n与时间频率f的关系，有式（5）：

当W=2时有式（6）：

功率谱为式（7）：

采用正弦波叠加，可得式（8）：

式中：φ为0到2π的随机值。

重构时将频率离散化后将正弦波叠加求得离散化的各级路面［9］。虚拟轨道车辆作为一种新型城市交通工具，其线路条件较为类似A级路面，因此文中仿真所用路面均采用A级路面。

1.4 轮毂电机控制方法

采用感应式异步轮毂电机，轮毂电机目前在新能源汽车中应用广泛，采用该类型电机可以简化车辆结构且便于采用新技术；而感应式电机同样结构简单、成本低廉且运行可靠。文中采用直接转矩控制，分别对8个车轮的转速进行控制［10-12］。其控制模型如图3所示。

图3 轮毂电机控制模型

1.5 循迹控制策略

循迹控制分为2部分：转向控制和车轮冲角控制，其循迹控制模型如图4所示。

转向控制采用横移PID控制［13-14］，实时检测每个车轮与目标轨迹的偏移量，分别输出转向力矩。该横移包括垂向激励和轮胎的侧偏特性在内引起的横移。其仿真模型如图4（a）所示。

车轮冲角控制目的是让车轮在弯道上能够实时处于径向位置，配合差动控制减小轮胎磨耗，具体采用实时监测车轮冲角，根据冲角大小输出转向转矩调整冲角。其仿真模型如图4（b）所示。

图4 循迹控制模型

1.6 差动控制方法

采用托森差速器的原理，监测一对轮胎的滑移率，当某侧滑移率超过临界值时，减小该侧输出转矩，增大另一侧转矩，完成驱动力的再分配，实现差动控制。其仿真模型如图5所示。

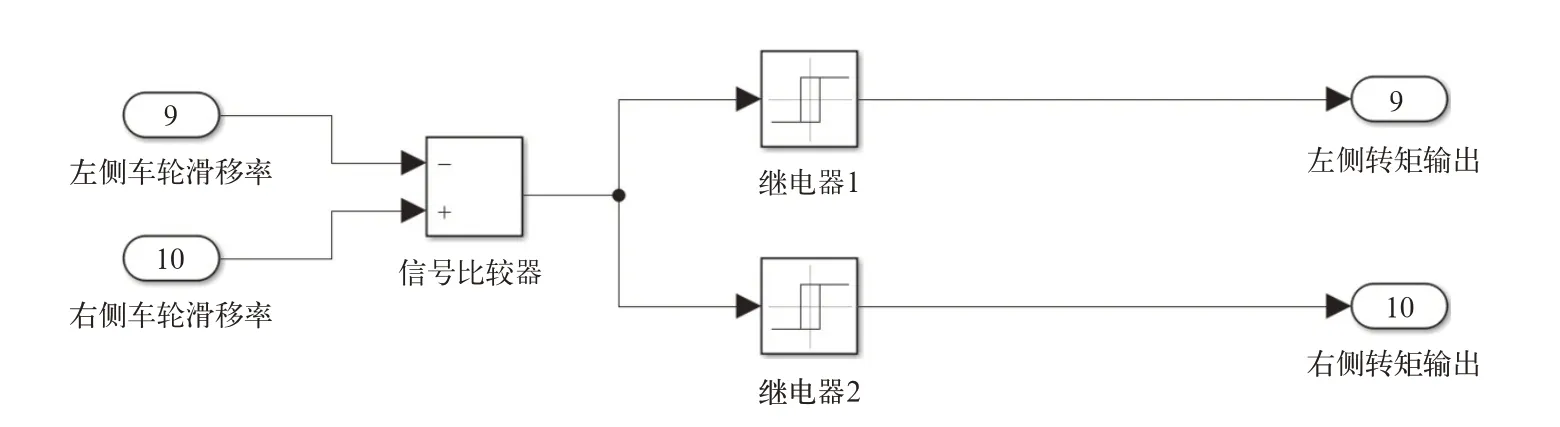
图5 差动控制系统模型

1.7 整车模型

整车模型包括循迹控制模块、电机驱动模块、差动控制模块、轮胎模型模块、车体动力学模块、悬架系统模块、车轮动力学模块、虚拟轨道路面模块等模块，各模块之间关系如图6所示。

图6 整车模型框图

2 二系垂向刚度/阻尼对车辆平稳性和可控性的影响

二系悬挂系统主要包括垂向减振器以及空气弹簧，悬挂参数主要包括空簧三向刚度以及垂向减振器提供的阻尼［15］。文中重点研究二系垂向刚度以及垂向减振器阻尼对车辆平稳性以及可控性的影响规律。

由于虚拟轨道车辆国内外尚无相应的相关评价标准［16-17］，文中借鉴传统铁路机车车辆常用的Sperling平稳性指标和循迹时车辆横移量的响应性能指标。需要指出的是，由于下文中虚拟轨道车辆是以60 km/h的中低速在采用A级路面谱的直道中仿真运行，A级路面代表最优的路面，其不平度相比其他的B～H级路面小很多，因此计算出的平稳性指标比较优。

2.1 二系垂向刚度

在研究二系垂向刚度对车辆平稳性的影响时，由于一系和二系垂向刚度属于串联的关系，在不同一系垂向刚度值下分析二系垂向刚度对车辆垂向动力学性能的影响规律，综合考虑二系悬挂装置的承载能力及减振性能，垂向刚度选取范围0.5～25 MN/m。

（1）平稳性

车辆运行速度60 km/h，A级路面，附着系数取0.7。车辆垂向平稳性和舒适度随二系垂向刚度值的变化曲线如图7所示。

图7 二系垂向刚度对平稳性影响

由图7可知，随着车辆二系垂向刚度的增加，垂向平稳性和舒适度均先增大，且随着一系垂向刚度的增加，平稳性指标稍有增加。

（2）可控性

虚拟轨道车辆属于自导向车辆，即在无人驾驶的情况下能沿着既定的轨道行驶，因此除了平稳性之外还需考虑车辆的循迹可控性。把车辆在与轨道有一定偏差情况下，逐渐向轨道靠近到保持循迹这一过程中车辆中心的轨迹视为循迹响应过程曲线。考察该曲线的超调量、上升时间以及调节时间，如图8所示。

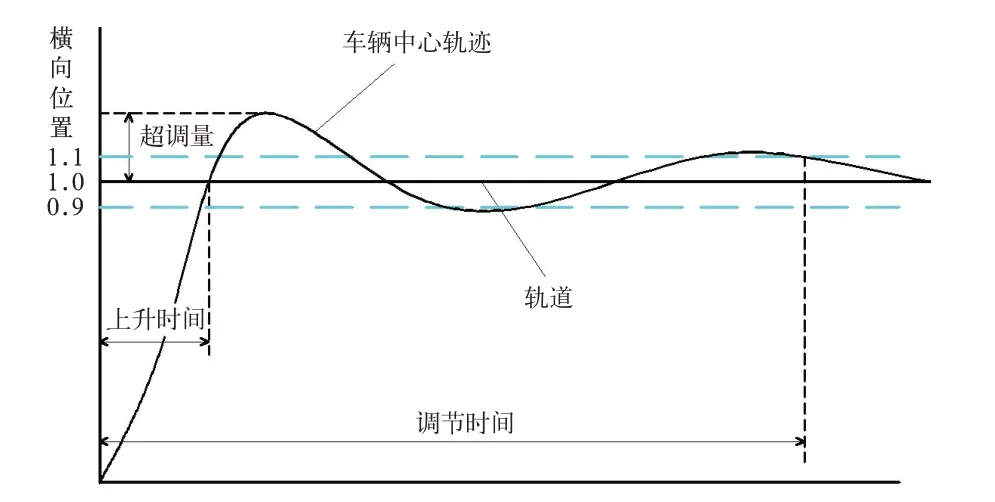
图8 可控性指标示意图

如车辆与轨道具有正的横向偏差，在循迹的过程中不会直接使得横向偏差为0，而是一个振荡—收敛的过程，其中出现的第一个波峰值为超调量，从0时刻到第一次横向偏差为0的时间为上升时间，调节时间指从0时刻到横向偏差收敛至10%的时间。若超调量、上升时间和调节时间越小，则车辆可控性越好。

车辆运行速度60 km/h，偏离预定轨迹1 m，A级路面，附着系数0.7。车辆中心横移量响应曲线的超调量、上升时间及调节时间随二系垂向刚度的变化曲线如图9所示。

由图9可知，随着二系垂向刚度和一系垂向刚度的增加，超调量、上升时间和调节时间均先减小后稳定，其中随着二系垂向刚度从0.5 MN/m增加到5 MN/m，三指标逐渐稳定，超调量减小20%左右，上升时间缩短10%左右，调节时间缩短近40%，由此可见车辆的可控性随着二系垂向刚度的增大而变得更优。

图9 二系垂向刚度对控制系统的影响

2.2 二系垂向减振器阻尼/节点刚度对平稳性的影响

考虑到减振器两端的橡胶节点刚度，改变节点刚度，与减振器阻尼值联合优化。橡胶节点的刚度值取10～30 MN/m，间隔5 MN/m，参考一般车辆的垂向减振器阻尼特性，取阻尼范围为10～50 kN⋅s/m。

车辆运行速度60 km/h，直线A级路面，附着系数取0.7。车辆垂向平稳性和舒适度随二系垂向减振器阻尼值的变化曲线如图10所示。

由图10可得，随着二系垂向减振器阻尼的增大，垂向平稳性和舒适度指标均减小，并逐渐趋于平稳。在减振器阻尼值较大时，随着二系垂向减振器节点刚度的增大垂向平稳性和舒适度指标均减小。

图10 二系垂向减振器阻尼/节点刚度对平稳性影响

文中还研究了二系垂向减振器阻尼/节点刚度对控制系统的影响，经过计算得出基本没有影响，不再赘述。

3 结论

（1）车体垂向平稳性与舒适度指标随二系垂向刚度的增加而逐渐增大，且在刚度值大于15 MN/m后趋于稳定。平稳性指标随着二系垂向减振器阻尼值的增大而减小，在阻尼值增大到40 kN⋅s/m后逐渐趋于平稳。

（2）循迹控制的响应超调量、上升时间及调整时间均随二系垂向刚度的增大而减小，且在刚度值大于5 MN/m后基本保持不变，可见适当地增大二系垂向刚度能提高系统的可控性。

（3）基于前面的分析可以看出二系垂向刚度对虚拟轨道车辆的平稳性和可控性的影响是互相矛盾的，提高可控性就会降低平稳性，反之亦然。由此可以为二系垂向刚度选取一个折衷值，可以看出可控性在刚度值大于5 MN/m之后基本不再变得更优，而此时车辆的平稳性指标也比较好。综合而言，当二系垂向刚度在5 MN/m左右时，能在保持较好的平稳性前提下兼顾车辆的可控性。

同时，当二系垂向减振器的阻尼值取40～50 kN⋅s/m时，车辆的平稳性较优。

从研究的虚拟轨道车辆悬挂参数对其平稳性和可控性的影响可以看出，对悬挂参数进行优化匹配可以使虚拟轨道车辆兼顾平稳性与可控性，为今后的虚拟轨道车辆二系垂向刚度及阻尼的取值范围提供理论参考。