有盖漏斗车卸货过程车体负压理论分析

李 静，康文泽

（中车太原机车车辆有限公司，太原030027）

有盖漏斗车卸货过程中车体承受负压，车体尤其是顶盖易发生塌陷，而国内铁道车辆相关标准中并未对负压工况提出考核。为保证车体强度满足使用要求，对有盖漏斗车卸货过程车体负压进行分析。由仿真分析可知漏斗车卸货过程负压接近极值，通过理论分析得出负压极值对有盖漏斗车通风孔设计具有一定的指导意义。

1 卸货过程分析

有盖漏斗车多数为重力卸货，货物由上面装入，卸货时用人力或风力开启漏斗底门，货物靠自身重力自动卸出。卸货过程中，货物快速地从下部流出，而空气不能及时进入到车体内部，导致车体内部压力急速降低，产生负压作用。负压增大到某一值时，车体会突然失去原来的形状，被压扁或出现波纹，载荷卸去后，车体不能恢复原状，即发生了屈曲或称为失稳。

2 车体负压理论计算过程中的假设

有盖漏斗车卸货过程中车体内的负压受货物状态、卸货时间、装货状态影响较大，同时也受卸货环境的影响；同时有盖漏斗车也并不是一个完全的密封结构，除了通气孔以外，顶盖和车体间仍然存在间隙，因此要完全理论分析出卸货过程中的负压变化及其困难。为分析有盖漏斗车卸货过程车体内的负压，做出以下假设：

（1）货物均匀卸出，流量不随时间和车内货物状态发生变化；

（2）忽略货物内部的间隙，即货物密实，颗粒间无空气；

（3）卸货过程中，空气不从卸货口进入车体内；

（4）忽略顶盖与车体间的间隙，即空气仅能从通风口进入车体内部；

（5）车体内压强大小不随位置的变化而变化；

（6）将车体内流体域分成两层，上层为空气、下层为货物，计算中主要考虑空气流动，且空气流动为定常流动，货物流动不做详细分析；

（7）把空气作为可压缩气体考虑，并且空气流动主要沿车体垂向，车体横截面沿垂向变化不大，故可按一元可压缩流考虑；

（8）假设气流流动过程中与外界无热量和功的交换、无黏性，则流动过程等熵。

上述假设中（1）对计算结果无影响，（2）、（3）、（4）使求得的计算结果偏大，（5）使计算结果不能充分反映通风口局部负压，（6）、（7）、（8）对计算结果影响较小。

3 可压缩流体一元定常等熵流动的基本方程

用于描述可压缩流体一元等熵流动的基本方程有3个，即

连续性方程为式（1）：

绝热方程为式（2）：

能量方程为式（3）：

式中：A为流管的横截面积；γ为气体的定压比热与定容比热之比；p为压强；ρ为密度；v为速度；V为体积。

此次理论分析的目的是确定卸货过程中有盖漏斗车内的负压极值，仅通过绝热方程和能量方程就能分析出漏斗车卸货过程中的负压极值。

4 有盖漏斗车卸货过程车体负压极值

4.1 绝热方程

t时刻车内的气体体积V、压强p；t到t+dt时间内，由通风孔进入车内气体体积为dV气，卸出货物体积为dV货；整个吸气过程绝热，由理想气体绝热过程方程［1］可得式（4）：

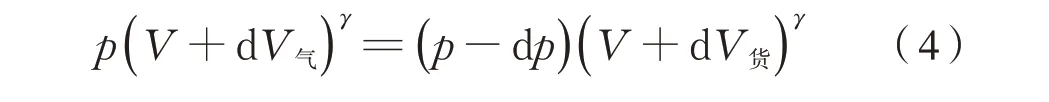
整理得式（5）：

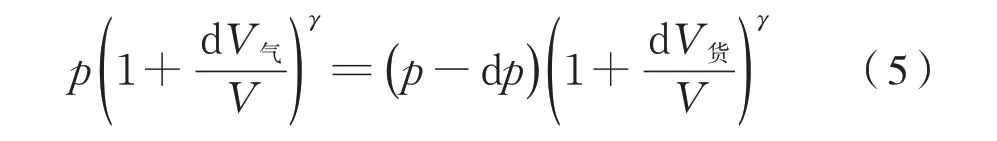
由广义二项式定理可得式（6）、式（7）：

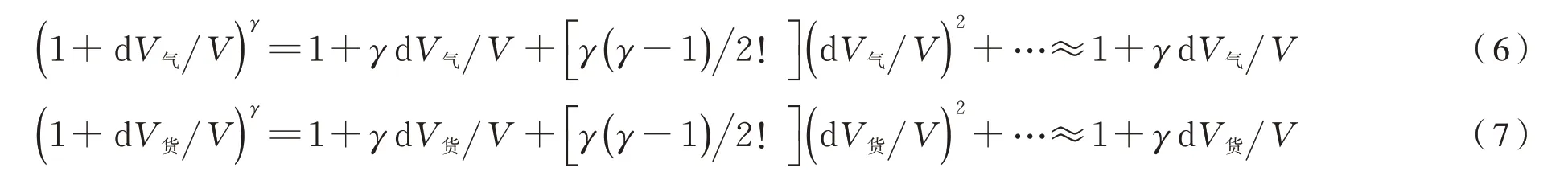
因此得式（8）、式（9）

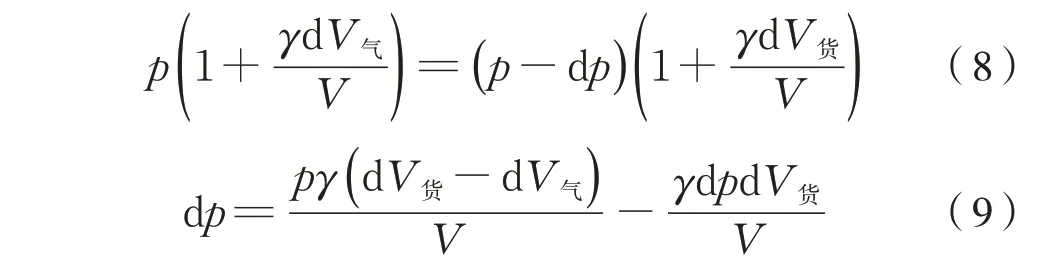
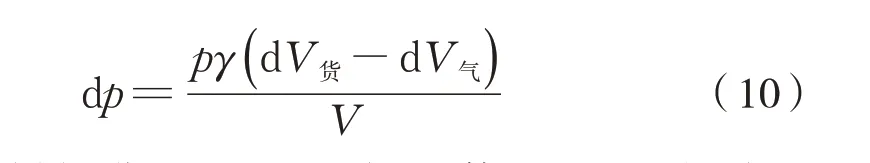
设t时刻卸货和吸入空气的体积流量分别为q货、q气，则有式（11）：

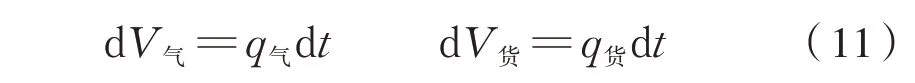
将上式代入式（10）可得式（12）：

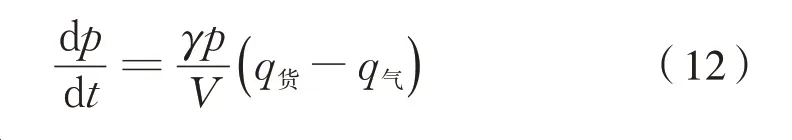
由式（12）可知，当q气=q货时车体气压达到极值，因为负压随着卸货时间的累积而增大，所以此极值为极大值。

4.2 通气孔内侧进口处空气流动的能量方程

有盖漏斗车卸货过程中，车体外部空气流动速度可看作为0，则其能量方程［2］为式（13）：

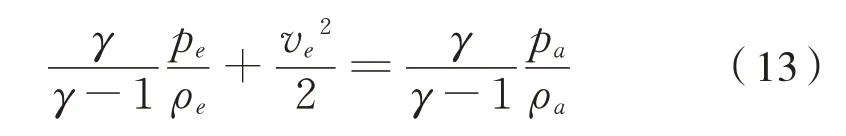
式中：pa为标准大气压下空气压强；ρa为标准大气压下空气密度；pe为通气孔内侧进口压强；ve为通气孔内侧进口气体流速；ρe为通气孔内侧进口处气体密度。

根据等熵过程方程可得式（14）：

联立式（13）和式（14）可得式（15）：

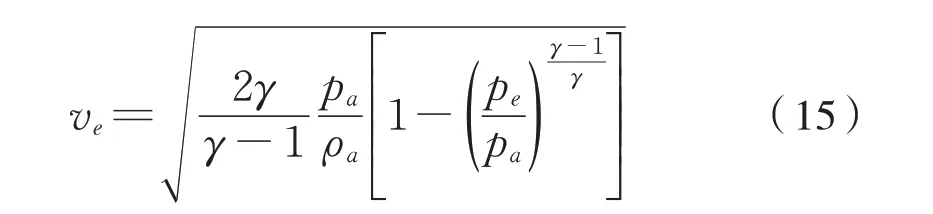
式（15）可写成式（16）：

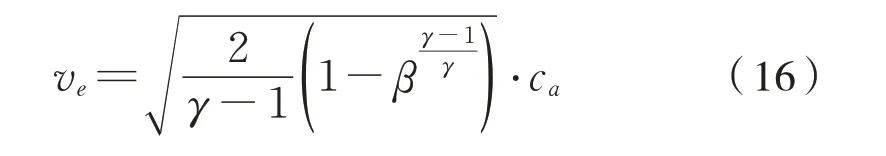
4.3 吸气和卸货的体积流量及气压极值

漏斗车底部卸货口截面积为A货，卸货速度为v货，体积流量为q货，则有式（17）：

通气孔中的空气进入车体内发生体积膨胀，通气孔中的体积流量不等于车体内的体积流量，但定常流动过程中同一流管中的质量流量不变［3］，则有式（18）：

式中：A气为通气孔总截面积；ρ气为车体内空气密度。

空气是理想气体，且流动过程等熵，根据泊松公式以及ρV=常数，可得pρ-γ=常数，则上式可写成式（19）：

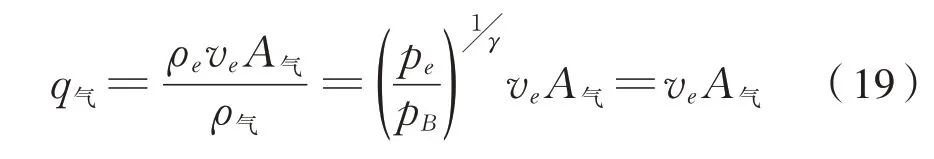
当q气=q货时，负压达到极值。设负压达到极值时β=βm，根据式（16）～式（19）可得式（20）：

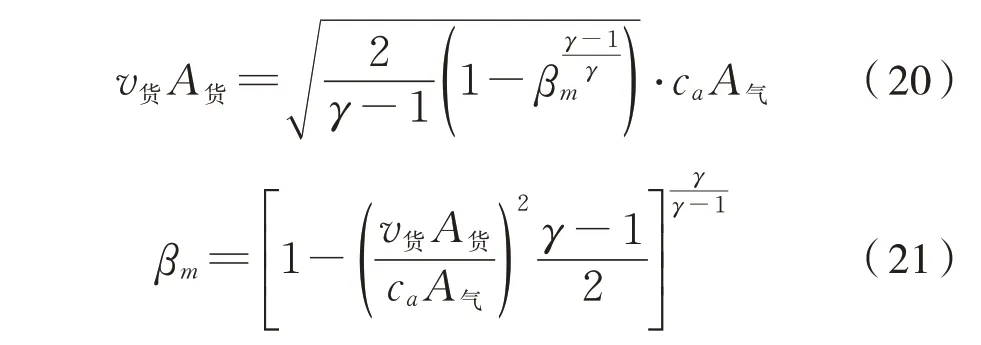
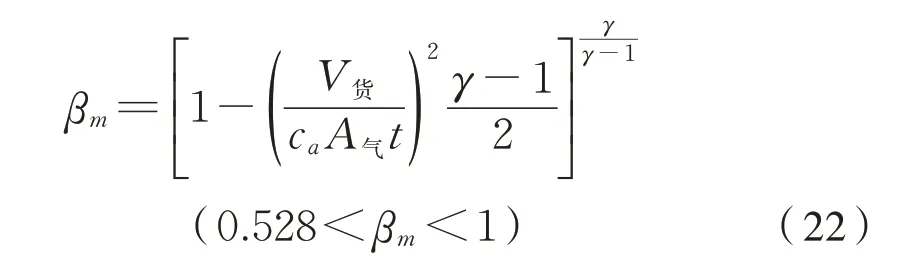
分析式（22）可得，有盖漏斗车卸货过程中车内负压极值与卸货总时间、通气孔的截面积有关：卸货总时间越短、通气孔总截面积越小，βm越小，车内负压极值越大。

5 某水泥熟料漏斗车车内负压极值理论计算

该漏斗车额定载重为70 t，水泥熟料堆积密度为1200 kg/m3，对于空气取ca=343 m/s、γ=1.4。将各值代入式（21）可得βm。不同卸货时间、通风孔直径下车体负压理论极值，见表1。

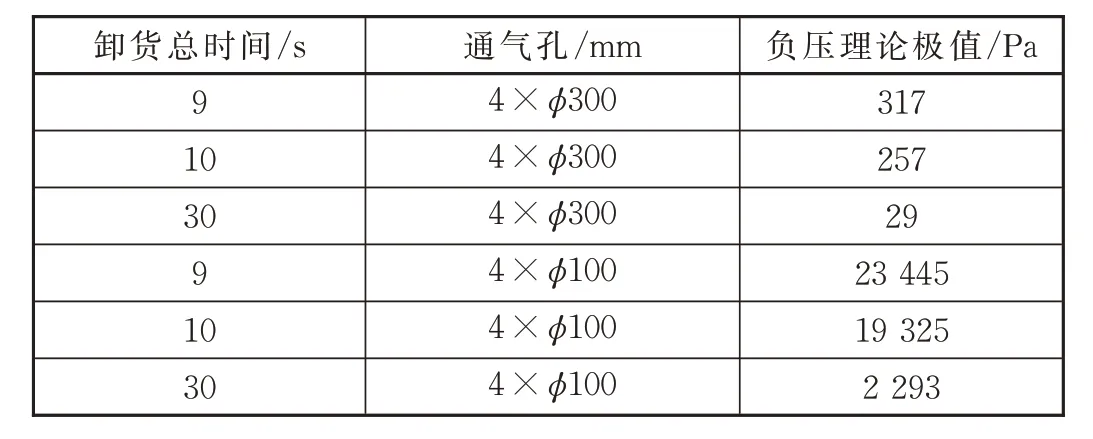
表1 不同卸货总时间、通风孔直径下车体负压极值

6 结论

通过以上理论分析及计算可得出以下结论：

（1）有盖漏斗车卸货过程中车内负压极值与卸货总时间、通气孔的截面积有关：卸货总时间越短、通气孔总截面积越小，车内负压极值越大。

（2）通气孔总截面积对负压极值影响较大，降低车体内部负压极值最有效的办法是增大通气孔总截面积。