多目标优化算法在列车运行控制中的应用研究

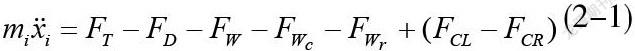
摘要：随着轨道交通行业的智能化、自动化发展，迫切需要计算智能方法提高铁路运营速度、降低列车能耗并提升列车自动化操纵水平。多目标优化算法在诸多行业领域均已得到广泛应用，本文将对多目标优化算法在轨道交通列车运行控制中的应用进行介绍，并指出下一步研究方向。

关键词：轨道交通;列车运行控制;多目标优化

列车运行控制优化问题是多属性的，受多种因素影响且随着时间不断变化，对于决策者而言此问题更复杂也更为广泛，因此多目标优化算法更能针对性满足多准则决策需求。

一、列车运行控制常用优化目标

列车运行控制优化属于多目标、非线性、大滞后问题，常见的优化目标函数为能耗最小化、舒适度最大化、停车精度最大化等。

1、能耗

交流传动电力机车再生制动会发电，耗电量减去发电量即为机车能耗.

2、舒适度

舒适度一般定义为纵向加速度变化的绝对值.

3、停车精度

停车精度是指列车实际停车位置与目标停车点差值的绝对值。

4、正点性

列车运行过程控制对正点要求非常高，准时性可以使用列车实际运行时间与运行图规定

时间之差的绝对值表示.

5、安全性

根据最大拉钩力和最大压钩力数值判断列车运行安全性.

二、列车运行优化模型

列车运行优化模型包括列车动力学模型和列车运行控制约束条件，建议针对特定工况和场景合理选择单、多质点模型。

1、列车动力学方程

列车多质点纵向动力学模型将每个车辆视作一刚性质点，整列车视作由钩缓连接成的质点链。

（2-1）

2、钩缓装置模型

重载列车缓冲器模型主要分为楔块-摩擦模型和胶泥-弹簧模型，缓冲器在不同工况对应

不同的加载/卸载特性曲线，车钩力主要和缓冲器位移、速度等相关。

3、列车运行优化约束条件

安全性约束：列车运行速度小于线路限速;列车停车点不在分相区范围;列车运行过程中车钩力不大于车钩缓冲器最大阻抗力。

精确性约束：列车停车点距离目标停车点不得低于规定数值;列车通过区间所需时间满足列车运行图要求。

操纵约束：牵引力和电制动力转化需经过不低于8秒左右的惰行工况，具体约束视具体场景和对象来设置。

三、多目标优化方法

多目标优化的目的是为决策者服务，即为决策者提供他们感兴趣的解（或解集）。多目标优化算法求解出的是帕累托最优解集，是折衷解的集合。

1、多目标优化算法分类

MOP算法在待优化目标函数个数较少时，表现出了较强的优化能力，得到的Pareto解集能够兼顾收敛性和分布性，MOP算法主要分为三大类：

1）基于Pareto支配关系的算法。代表性算法有NSGA-II[4]。

2）基于分解策略的算法。通过分解将帕累托前沿多目标问题转化为多个子问题，经典算法有MOEA/D[6]。

3）基于评价指标的算法。根据评价指标，如超体积、反世代距离等，选择精英个体参与迭代进化，代表算法有HypE[6]等。

2、多目标优化算法在列车运行控制中的应用

1999年C.S.Chang较早应用多目标优化算法在轨道交通领域[1]，其使用多目标差分进化算法调整模糊隶属度函数进而优化列车运行，使得列车运行准时、节能且舒适度高;王龙达等基于偏好信息的多目标遗传粒子群算法求解能耗、舒适度、停车误差和舒适度综合较优的列车操纵结果;王龙达[2]等基于偏好准时和节能的多目标鲨鱼优化算法改进了列车运行过程并在硬件在环实验环境dSPACE仿真进行了验证;张惠茹[3]等基于改进的NSGA-II获得了高速列车节能驾驶曲线集，实现了能耗-时间平衡的节能驾驶曲线集生成。

四、下一步研究展望

根据列车运行控制模型与优化算法研究现状可知，当前求解多目标函数大多使用的是自变量约束的MOP算法，不同场景和工况的列车运行优化应合理选择优化目标，使用更高效寻优算法，并侧重约束多目标优化算法，并加大实际现场应用和验证，不断提高算法求解能力和模型的精确度。

参考文献

[1]Chang C S， Xu D Y， Quek H B. Pareto-optimal set based multiobjective tuning of fuzzy automatic train operation for mass transit system[J]. IEE Proceedings-Electric Power Applications， 1999， 146（5）： 577-583.

[2]王龙达， 王兴成， 刘罡， 等. 基于偏好的列车运行过程多目标鲨鱼优化算法[J]. 仪器仪表学报， 2020， 41（10）： 247-258.

[3]张惠茹， 贾利民， 王莉. 基于Pareto多目标优化的高速铁路列车节能驾驶曲线集生成[J]. 铁道学报， 2021， 43（3）： 85-91.

[4]Deb K， Pratap A， Agarwal S， et al. A fast and elitist multiobjective genetic algorithm： NSGA-II[J]. IEEE Transactions on Evolutionary Computation， 2002， 6（2）：182-197.

[5]Zhang Q， Hui L. MOEA/D： A Multiobjective Evolutionary Algorithm Based on Decomposition[J]. IEEE Transactions on Evolutionary Computation， 2007， 11（6）：712-731.

[6]Bader J， Zitzler E. HypE： An Algorithm for Fast Hypervolume-Based Many-Objective Optimization[J]. Evolutionary Computation， 2011， 19（1）：45-76.

作者簡介：刘颖南，1994.05.11，男，汉族，安徽亳州市，硕士研究生，助理工程师，列车自动驾驶