基于熵权-TOPSIS高模量沥青路用路用性能综合评价
李新鹏 赵文婧


摘 要:为定量分析高模量沥青最佳改性剂掺量,为选择高模量沥青提供一定参考。本文旨从综合高模量沥青路用性能的角度出发,通过熵权法定量计算得到了混合料抗高温、抗低温、抗水损、抗力性能在综合系统中各自所占的权重;再通过TOPSIS法建立综合评价模型,得到各掺量改性剂的优劣值,优劣值结果如果显示越大的则表明沥青混合料的综合性能越优异。结果表明本模型可以为综合选择高模量沥青提供一定参考。同时该模型还有其他拓展的空间,如若将成本等其他相关因素考虑进该模型中,也可以应用于级配、集料等因素的确定。
关键词:综合路用性能;熵权法;TOPSIS;高模量沥青
1 研究意义
随着时代的发展进步,我国交通建设也日益趋于强大,在发展过程中,我国的公路里程在日益增加,这使得对一般建设公路所需的主要材料——沥青的性能和各项指标等需求也越来越高。但近年来,交通压力的增加使得沥青路面损坏严重,严重损害的路面的使用寿命。施工建设需求的方面越来越广泛但更为严谨,这就要求研发出一款性能更为优越的沥青混合料,这也就使得高模量沥青凭借其强劲的路用性能进入了国内研究者的视野。
相比于普通沥青,高模量沥青抗车辙、抗水损、抗低温开裂等能力更加优秀。但是高模量沥青改性剂的掺量并不唯一,不同掺量改性剂对混合料的各性能的提升也不一样。本文从高模量沥青综合性能的角度出发,建立熵权-TOPSIS模型,找到最佳综合性能下的改性剂掺量。
2 指标赋权
截至目前为止已有许多计算综合评价指标权重的方法,如“层次分析法”(AHP)、“主成分法”、“熵权法”等。AHP是根据相关专家根据自身对专业的认识,对相应的指标之间的重要程度进行打分,得分越高则该指标权重越大,主观性强,容易产生较大误差。主成分法则通过信息浓缩对指标进行二次分类,减少指标个数,一般适用于指标较多的情况。而熵权法是一种客观赋权方法,其借鉴了信息熵思想,通过计算指标的信息熵,根据各个指标标志值的差异程度来进行赋权,从而得出各个指标相应的权重。本文用到了高温稳定性、水稳定性、低温稳定性与力学性能四个指标,指标数目较少,因此选用熵权法对指标进行赋权。
2.1 原数据处理
本文参考文献[1]实验数据,并根据数据构造出一个的原始数据矩阵,其中为不同掺量的PR-M改性剂,为对应的四个指标。本文采用极小型指标(负向指标)来评价高温稳定性。其余指标均为极大型指标(正向指标),故需分别按照以下公式进行归一化处理,得到归一化后的指标数据矩阵。在此,为避免求熵无意义,本文对处理后数据为0的值改为0.01。
其中公式(1)适用于极大型指标,公式(2)适用于极小型指标。
2.2 计算比重
分别计算各项指标在各样本所占的比重,即指标在第个样本中所占的比重,得到数据的指标占比矩阵。
(3)
2.3 计算指标的熵与差异度
熵权法的赋权是根据各指标的差异度进行的,差异度的值会直接影响各指标权重大小,因此在得到指标占比矩阵后需要计算各指标的熵值与差异度。具体公式如下:
(4)
(5)
其中为指标的熵,。
为指标的差异度,。
2.4 计算指标权重
在得到各指标的差异度后,根据公式(6)可计算得到四个指标权重向量。权重向量为w={0.217 0,0.191 8,0.202 9,0.388 3}。
(6)
3 综合性能评价
为综合评估高模量沥青的路用性能,本文在此提出使用TOPSIS法(又称优劣解距离法)构建评价模型。TOPSIS可充分利用已知样本数据,在有限的样本中找出最优方案或最劣方案,根据当前评价样本各指标与正负理想解相对距离,来最终做出评价。
3.1 指标数值矩阵加权
由于在熵权法已经对数据进行处理,且其处理方式与TOPSIS法一致,本文在此直接使用不再对初始指标数据进行处理,直接使用上述权重向量对指标数据矩阵进行加权,得到加权矩阵。计算公式如下:
(7)
3.2 最优最劣距离的确定
在TOPSIS法中,为求解最优、最劣距离,首先需要求出每一指标的最佳样本和最差樣本,然后计算各个样本与最佳样本与最劣样本的距离,即差值和的平方根。具体如下所示:
(8)
(9)
其中、为每一指标的最佳样本和最差样本;
、为每一方案距最佳样本和最差样本的距离。
特别地,越大,则说明该样本距离最佳样本的距离越远,那么该样本就越差; 越小,则说明该样本距离最佳样本的距离越近,那么该样本就越优秀。反之则为大小的解释。
3.3 各样本优劣值的确定
各样本的优劣值为该样本距最差样本的距离与该样本下最佳样本、最差样本的距离和的商值。其值越大,说明该样本综合性能更加优秀。其公式如下:
(10)
3.4 结果分析
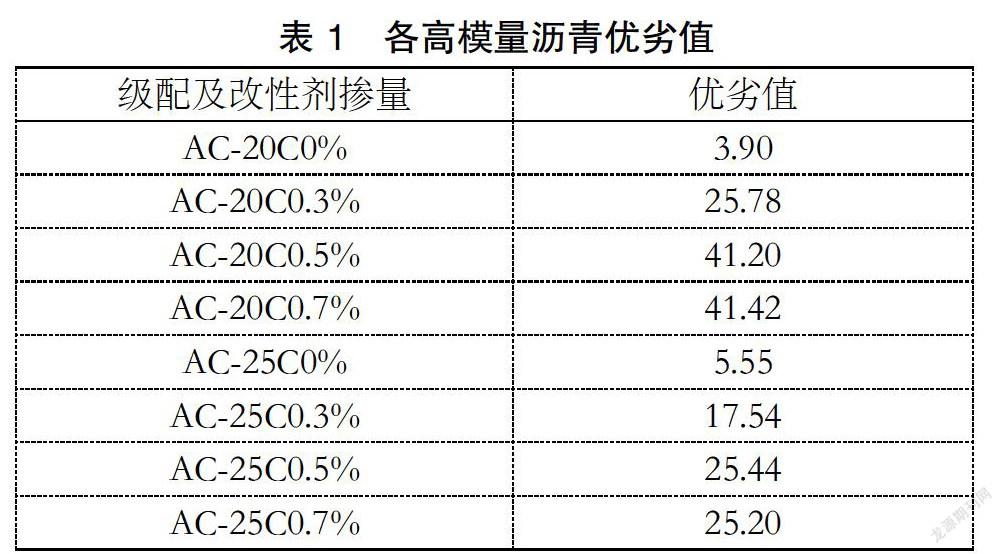
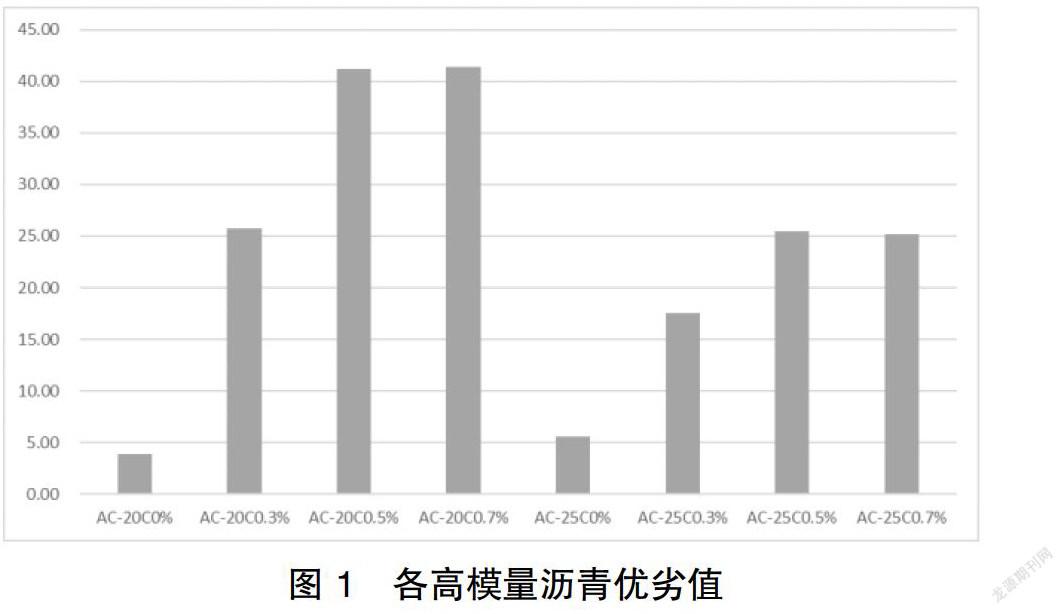
笔者通过MATLAB对上述过程用代码进行实现,得到各高模量沥青的优劣值,为更直观的展示结果之间的差距,笔者将各混合料的优劣值均扩大50倍处理,如表1、图1所示:
通过上述步步的分析,显而易见的是,掺有PR-M改性剂的沥青混合料的综合性能明显比未掺加有大幅度的提升。其中,当级配位AC-20C时,0.5%与0.7%掺量的沥青混合料的综合性能大致相当。从节约成本角度来看,应选用0.5%掺量。在掺量相等的前提下,级配AC-25C沥青混合料综合性能均低于级配为AC-20C的混合料,与实际一致。
4 结论
本模型没有AHP法主观性的影响,可以充分使用实验数据进行分析,对数据的利用程度高,得到的结果更加客观,为高模量沥青改性剂掺量的确定提供了一定的参考。同时,本模型不仅可以用于确定改性剂最佳掺量,也可以应用于级配、集料等因素的确定,应用范围广。
参考文献:
[1]张晨.PR.M高模量沥青混合料在公路中的应用研究[D].中南林业科技大学,2016.
[2]王超.PR_MODULE高模量沥青混合料路用性能及其应用技术研究[D].内蒙古农业大学,2014.
[3]施晓强.高模量沥青混合料的路用性能评价[J].公路工程,2014(6):175-179.
[4]司守奎,孙兆亮.数学建模算法与应用[M].北京:国防工业出版社,2017.

