线段中点与角平分线的类比学习

陈妹

摘 要：在平时授课过程中去渗透类比思想也是新课标所倡导的，这就要求我们在实际数学教学和学习过程中，引导学生学会如何将已有知识和方法迁移到新问题的解决中来，这对于学生的思维拓展有很大帮助，从而进一步提高學生学习数学的兴趣.本文主要以线段的中点和角的角平分线为载体，通过知识的横向迁移，让学生能够在具体的解题中体会线段中点与角平分线之间的区别与联系，并能够总结出解题方法和规律.

关键词：初中数学;线段中点;角平分线;类比学习

在数学学习和研究中，类比是一种重要的思想方法，也是合情推理得一种重要形式.类比是根据两个对象或两类事物的一些属性相同或相似，猜测另一些属性也可能相同或相似的思维方法，亦是由特殊到一般的过程.

一、线段中点与角平分线的概念

1.线段中点：把一条线段分成相等的两部分的点，叫这条线段的中点.

2.角平分线：从一个角的顶点引出一条射线，把这个角分成相等的两个角的，则这条射线叫这个角的角平分线.

二、单中点与单角平分线问题的类比

考查了两点间的距离，利用线段的中点的性质转化线段之间的和差关系是解题的关键，类比2综合考查了角平分线的定义，角的和差等相关知识，重点掌握角平分线的定义.这两题从本质上来讲，都是根据已知条件求解线段的长度或者角的度数，都是求解定值的过程，也都是由特殊到一般的过程，注重引导学生运用整体思想说理，同时要注意在不同的情况下灵活选用线段中点或角平分线的不同表示方法，有利于解题的简洁性.

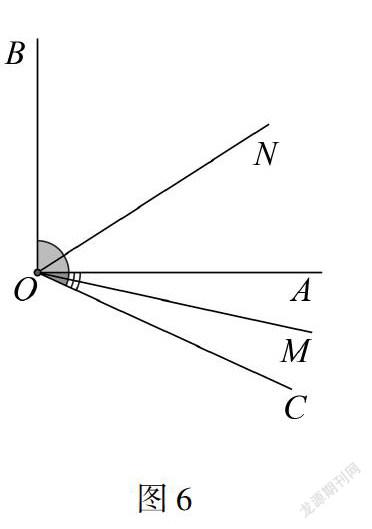
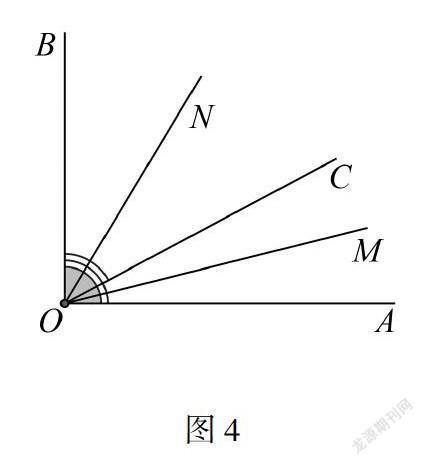
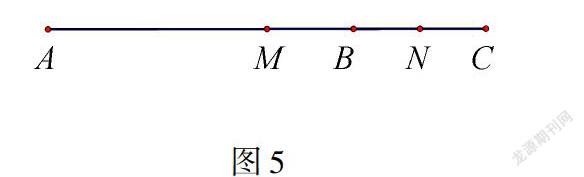
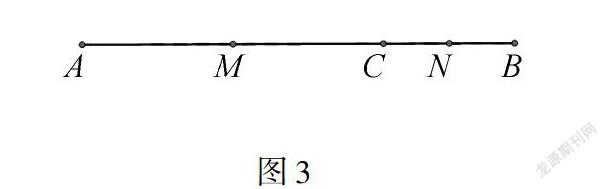
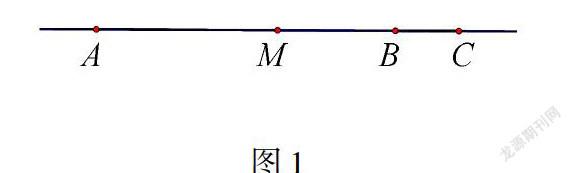
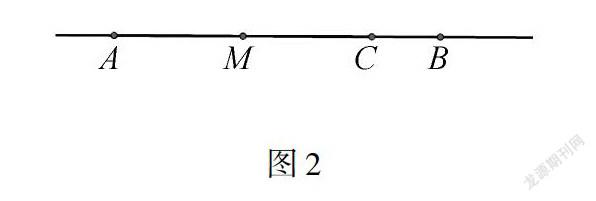
同样的，类比“例2”与“类比2”，也很容易求出这两题的一般结论.此时不妨引导学生去总结一下求双中点和双角平分线问题的一般规律.在双中点问题中的一般性结论：在同一条直线上，有公共端点两条线段中点之间的距离就等于，不重合的那两端点距离的一半.通过类比，我们可以得到在双角平分线问题中的一般性结论：当两个角的顶点及边重合时，两个角的平分线所组成的角，就应该等于不重合的两边所构成角的一半.

诚如数学家G·波利亚说：“类比是一个伟大的引路人.”在数学问题的解决中，很多数学家就是利用类比法猜想某些结论的成立，并对之进行证明，推进了数学的发展.在本文中通过对中点定义、角平分线定义在解题中应用的类比，不仅可以让学生自己得到类似知识点的概念，引导学生体会应用由特殊到一般的思想方法，探索图形中的一般规律，而且有利于在学习过程中培养勤于思考、乐于探究的学习习惯，提高学生在数学学习中的自信心和积极性.在数学学习研究中，用到的往往不是单一的思想方法，比如本文中还涉及到数形结合思想、分类讨论思想，甚至对于题目的处理也可以运用方程思想来解决.这也再次要求我们教师在平时的教学中不断渗透数学思想方法，重视培养学生的核心素养，教会学生去思考，做好学生数学学习的引路人.

参考文献：

[1]卫志勇.利用类比法学习线段中点与角平分线[J].初中数学教与学，2016（12）：36+41.

[责任编辑：李 璟]