新教材“平面向量及其应用”内容比较研究
李保臻 巩铠玮 孟彩彩 陈国益



摘 要:向量学习有助于促进学生数学学科核心素养的提升及应用能力的提高. 以人教A版、北师大版和湘教版教材中“平面向量及其应用”内容为研究对象,主要从知识结构、栏目设计、内容广度与深度、数学文化渗透四个维度进行比较分析. 发现三版教材中的“平面向量及其应用”内容在上述四个方面各具特色,由此获得相关启示.
关键词:新教材;平面向量及其应用;内容比较
教材是体现教学内容和教学要求的重要载体,与教师和学生共同构成教育活动的基本要素,承载着课程标准的基本理念和具体要求,影响着教学的成效与学校教育的质量. 随着《普通高中数学课程标准(2017年版)》(以下简称《标准》)的颁布,多个版本的新教材也相继出版,其中人教A版、北师大版、湘教版教材无论从使用范围还是影响程度来说都具有一定的代表性. 此外,“平面向量及其应用”又是高中数学几何与代数主题的重要内容,在一定程度上反映了数学教材编写者的价值取向和编写风格. 因此,对这三版教材中向量相关内容的编写情况进行比较很有必要.
向量理论具有深刻的数学内涵、丰富的物理背景,为解决数学和物理中的相关问题提供了新的工具,是沟通代数与几何的桥梁. 向量作为代数研究对象,其中蕴含着丰富的运算,它的学习可以促进学生数学运算、数学建模等素养的发展. 同时,作为几何研究对象,借助向量可以表征并解析点、线、面的位置关系,对学生理解空间图形的几何性质具有重要意义.
对相关文献进行梳理,发现我国学者对高中数学向量的研究大多聚焦于课程内容、习题比较、价值意义等方面,而对不同版本,尤其是《标准》配套的新教材中向量内容的设置特色挖掘不够,且相关研究较少. 鉴于此,本研究选取依据《标准》编写的人教A版、北师大版和湘教版教材,对“平面向量及其应用”内容的不同维度进行比较,分析其设计思路的异同与特色,以期为一线教师教学提供一些参考.
一、研究设计
1. 研究对象
人教A版《普通高中数学教科书·必修(第二册)》(以下统称“人教A版教材”)第六章“平面向量及其应用”;北师大版《普通高中数学教科书·必修(第二册)》(以下统称“北师大版教材”)第二章“平面向量及其应用”;湘教版《普通高中数学教科书·必修(第二册)》(以下统称“湘教版教材”)第一章“平面向量及其应用”.
2. 研究方法
本文以文本分析法和比较研究法为主要研究方法,对三版教材中的“平面向量及其应用”内容从知识结构、栏目设计、内容广度与深度、数学文化渗透四个维度进行比较分析,并依此得出研究结论和启示.
二、研究结果与分析
1.“平面向量及其应用”内容知识结构的比较分析
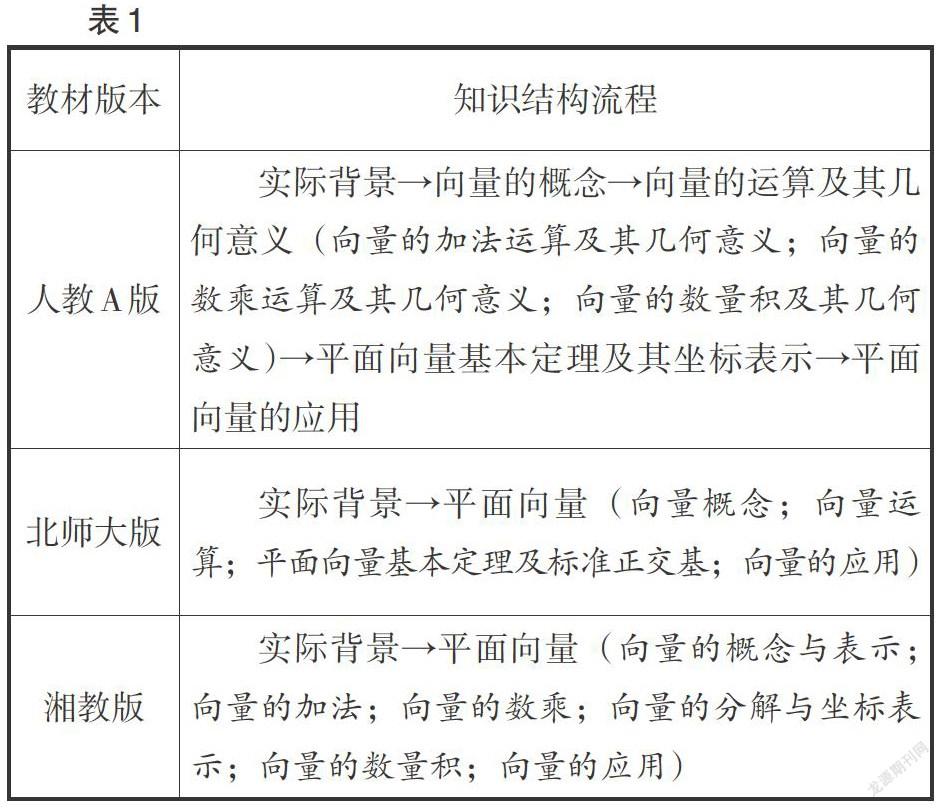
教材的知识结构是按照教材内容特点、学生的认知水平、心理特征,以及教师组织教学的特征设置的,它是进行教学设计的关键. 知识结构的建立,可以帮助学生构建知识框架,进而整体把握教学内容,拓宽思考问题的视角,培育学科核心素养. 现将三版教材中“平面向量及其应用”的知识结构流程呈现如表1所示.
通过表1发现,虽然在三版教材中“平面向量及其应用”内容所处的章节不一致,但内容的主线基本一致,其知识系统都涵盖了基本知识点,知识结构都符合学生的发展要求及《标准》的理念,即引导学生在了解向量实际背景的基础上,学习平面向量的概念、运算及其基本定理,同时让学生运用所学的向量知识解决相关问题. 接着探索三角形边和角度的关系,从而引出正弦定理和余弦定理,从中体会并发现向量的实际应用. 总体来说,三版教材都从代数角度突出了向量的运算功能,从几何角度凸显了向量的几何意义,从物理角度丰富了向量的知识背景.
相比而言,三版教材中的向量知识结构在实际背景与概念分布上基本一致,但在运算及应用内容分布上存在较大差异. 在向量的运算方面,人教A版教材和北师大版教材将加法、数乘、数量积作为整体进行设计,湘教版教材将加法、数乘、数量积单独成节;在向量的应用方面,北师大版教材对度量关系、位置关系进行了介绍,而人教A版教材和湘教版教材从结构来看对此并未涉及. 总的来说,人教A版教材更注重向量知识的系统性和整体性,其对向量知识结构的设计显得更連贯自然;北师大版教材不仅注重整体性设计,而且侧重向量度量与位置关系的渗透;湘教版教材中向量加法、数乘、数量积单独成节的设计使得知识点更为详尽.
2.“平面向量及其应用”内容栏目设计的比较分析
高中数学教材栏目的设计,是为了倡导学生采用自主学习及合作学习等方式,改变传统数学课堂教学中死记硬背的情况,进而在理解掌握的基础上不断完善自身的学科核心素养.《标准》基本理念中明确提出:高中数学教学以发展学生数学学科核心素养为导向,引导学生把握数学内容的本质. 此外,提倡多种学习方式,促进学生实践能力和创新意识的发展. 三版教材中都设计了新颖的数学活动栏目,引导学生自主探究学习,感悟数学的应用价值、文化价值等. 现将三版教材中“平面向量及其应用”内容的主要栏目呈现如图1 ~ 图3所示.
研究发现,人教A版教材设计“思考”“探究”“复习巩固”“综合运用”“拓广探索”栏目,是为了引导学生理解向量的本质,让学生体会向量知识中蕴涵的数学思想方法,进而培养学生发现问题、提出问题、分析问题、解决问题的能力,以期不断完善学生的学科能力;北师大版教材设计“思考交流”“实例分析”“抽象概括”“分析理解”“问题提出”栏目,其注重向量知识与实际生活的联系,引入具有时代性和现实感的素材实例,意在培养学生的向量应用意识,并借此不断促进学生实践能力的提高及数学学科核心素养的提升;湘教版教材设置“学而时习之”“温故而知新”“上下而求索”栏目,其特色在于古文式的栏目名称富有创新性,重在培养学生的学习兴趣. 三版教材中向量的栏目设计皆意在培养学生会用数学眼光观察世界、会用数学思维思考世界、会用数学语言表达世界的能力.
3.“平面向量及其应用”内容广度与深度的比较分析
(1)“平面向量及其应用”内容广度.
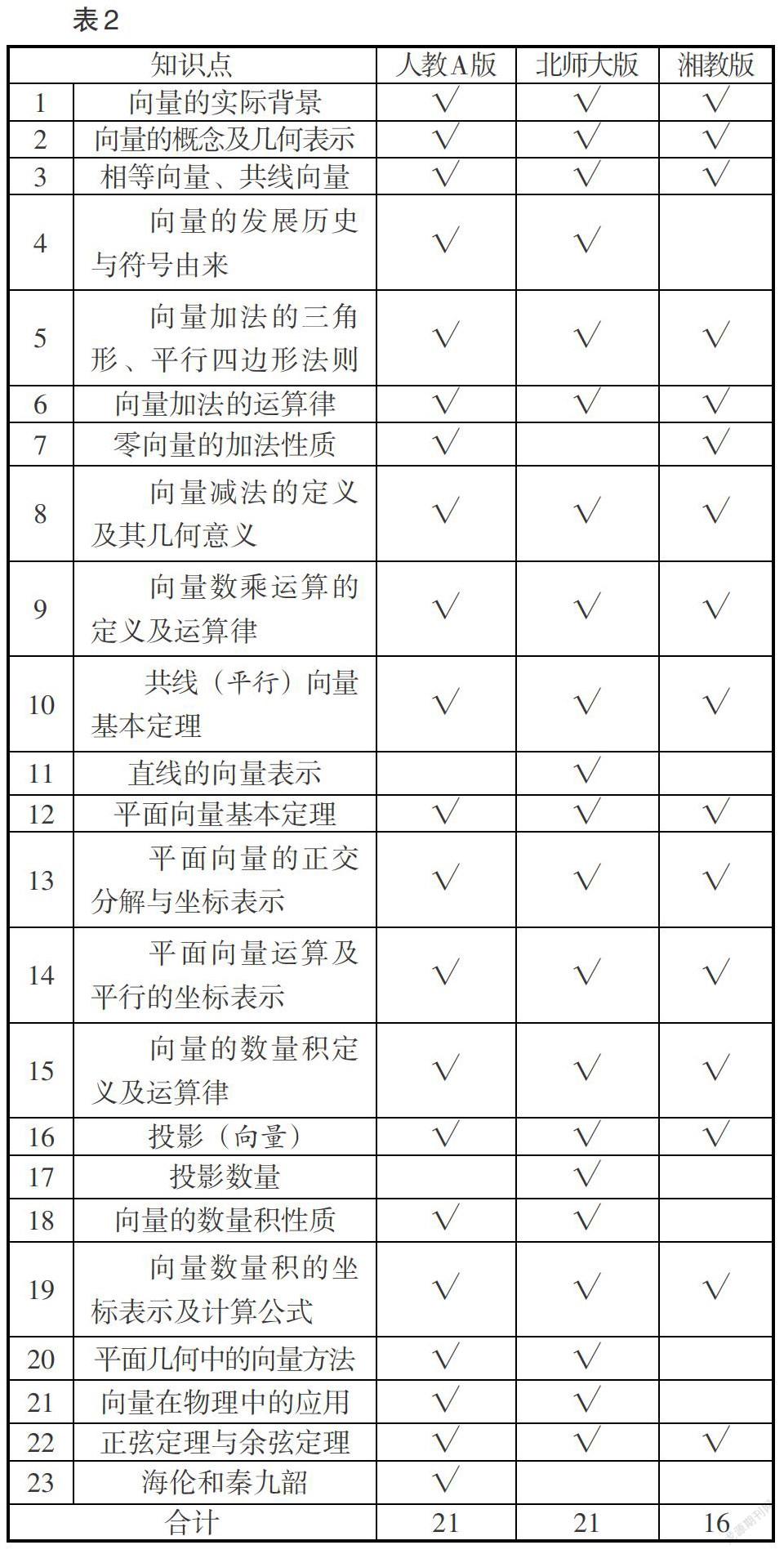
内容广度指内容所涉及的范围和领域的广泛程度. 以下采用知识点的数量刻画内容广度,现将三版教材中“平面向量及其应用”的内容广度呈现如表2所示.
从表2中发现,人教A版教材的课程广度为21;北师大版教材的课程广度为21;湘教版教材的课程广度为16,即北师大版教材与人教A版教材中“平面向量及其应用”的内容广度基本相似,而湘教版教材中“平面向量及其应用”的内容广度较小.
通过具体分析发现,对于“零向量的加法性质”这一知识点,人教A版教材和湘教版教材进行了具体说明,而北师大版教材并未提及;对于“直线的向量表示”知识点,北师大版教材重点描述,而人教A版教材与湘教版教材皆在习题中渗透;对于“投影数量”知识点,北师大版教材介绍投影数量是数量积的特殊情况,而在人教A版教材與湘教版教材中并未涉及;对于“向量的应用”知识点,人教A版教材与北师大版教材从几何与物理两个角度进行介绍,而湘教版教材将其渗透于习题中,让学生在习题练习中理解、掌握此知识点;对于“向量的数量积性质”知识点,人教A版教材与北师大版教材均具体呈现,而湘教版教材仅在习题中渗透;对于数学文化的相关知识点,人教A版教材涉及向量的发展历史与符号由来、海伦和秦九韶,北师大版教材涉及向量的发展历史与符号由来,湘教版教材在此章节中未呈现具体数学文化知识.
(2)“平面向量及其应用”内容深度.
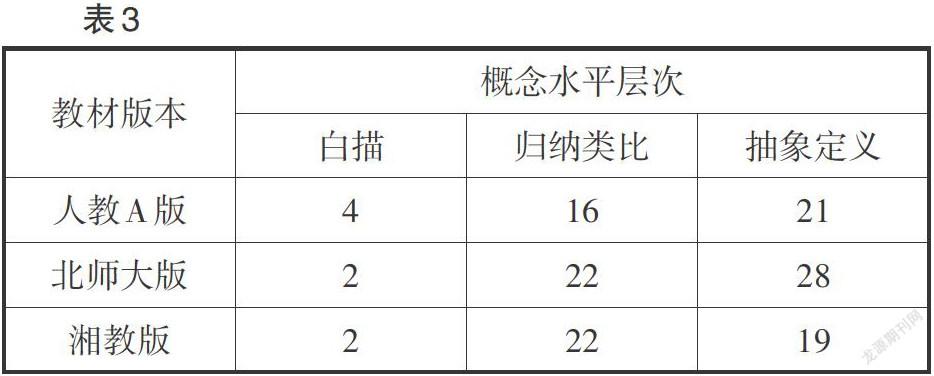
内容深度泛指内容所需要的思维深度,涉及概念的抽象程度及概念之间的关联程度等. 对“平面向量及其应用”内容运用白描、归纳类比、抽象定义三个水平进行分析,进而呈现其内容深度. 其中,“白描”是指用最简练的笔墨,描画出鲜明生动的对象;“归纳类比”是一种推理方法,是基于两种不同事物或道理间的类似,借助喻体的特征,通过联想对本体加以修饰描摹的一种文学修辞手法,也是一种说理方法;“抽象定义”是指直接概括被定义变量的性质或特征. 以平面向量章节的相关概念为例,通过画有向线段表示向量,则属于白描的形式;借助线段与方向表示向量的概念,则属于归纳类比的形式;直接定义“平面向量及其应用”章节的相关概念,则属于抽象定义的形式. 现将三版教材中“平面向量及其应用”的内容深度呈现如表3所示.
三种深度水平层次的划分代表概念分布的不同:白描层次代表概念深度较低;归纳类比层次代表概念深度适中;抽象定义层次代表概念深度最高. 由表3反映出,三版教材都在白描层次有所涉及,人教A版占比约为10%,北师大版占比约为4%,湘教版占比约为5%;在归纳类比层次,人教A版占比约为39%,北师大版占比约为42%,湘教版占比约为51%;在抽象定义层次,人教A版占比约为51%,北师大版占比约为54%,湘教版占比约为44%.
对比三版教材中的数据,发现人教A版教材中概念分布在白描层次占比最大,归纳类比层次占比最小,抽象定义层次占比居中;北师大版教材中概念分布在白描层次占比最小,归纳类比层次占比居中,抽象定义层次占比最大;湘教版教材中概念分布在白描层次占比居中,归纳类比层次占比最大,抽象定义层次占比最小. 由此可见,人教A版教材中的概念难度居中,北师大版教材中的概念难度最大,湘教版教材中的概念难度最小. 综上,北师大版教材中“平面向量及其应用”的内容深度最大,人教A版次之,湘教版最小.
4.“平面向量及其应用”内容数学文化渗透的比较分析
重视数学的文化价值是数学教育发展的趋势,而数学文化的渗透推动着数学教学的发展和学生数学素养的提升. 简而言之,数学文化是数学知识、思想方法及其在人类活动的应用,以及与数学有关的民俗习惯和信仰的总和,它具有规范特征、审美特征、认知特征、历史特征、价值特征. 因此,高中数学教学不仅包括学科知识的学习,更蕴含着数学文化的传播学习. 由此可见,数学文化应当以适当的形式渗透到学生学习过程之中,内化为学生的认知并驱动学生高效学习数学,让学生在数学学习的过程中生成必备品格、形成关键能力. 现将三版教材“平面向量及其应用”内容的数学文化渗透情况统计呈现如表4所示.
从表4中发现,人教A版教材通过阅读与思考窗口向学生展示向量及向量符号的发展历程,让学生对向量进行深入了解,同时引出海伦和秦九韶两位数学家,重在让学生体会数学的人文性和历史性,既让学生学会已知三角形三边直接求解三角形面积的方法,也让学生了解到两位数学家在数学领域的杰出贡献,进而学习数学家为科学奉献的精神,借此拓宽学生的视野,培养学生的探索精神;北师大版教材通过阅读材料窗口向学生介绍向量的发生、发展过程,即向量的发展历史与符号由来,从而培养和提高学生的数学素养,激发学生的求知欲和探索精神;湘教版教材在“平面向量及其应用”章节中未渗透数学文化.
相比而言,人教A版教材的数学文化渗透更全面,更有利于教师的教和学生的学. 它不仅从向量的发生、发展过程及实际应用角度渗透数学文化,也从数学家海伦和秦九韶的生平和贡献角度引入与向量有关的数学文化.
三、研究结论及启示
1. 研究结论
通过对人教A版教材、北师大版教材和湘教版教材中“平面向量及其应用”内容的不同维度进行比较分析. 发现三版教材具有以下特征.
(1)向量知识结构的编排方面.
三版教材中“平面向量及其应用”内容的知识结构在实际背景与概念分布上基本一致,但在运算及应用内容分布上存在较大差异. 相比而言,人教A版教材在介绍向量概念及运算的基础上呈现基本定理与应用的知识点,其更注重向量知识的系统性和整体性设计;北师大版教材不仅注重整体性设计,还从物理的角度引出向量相关知识点,同时侧重向量“度量关系”与“位置关系”的几何应用;湘教版教材注重将“向量的加法”“向量的数乘”“向量的数量积”单独成节设计,使得知识点内容更为详尽具体.
(2)向量内容栏目的设计方面.
三版教材中“平面向量及其应用”内容的栏目设计不同,充分体现了编写者对《标准》课程理念的不同理解. 相比而言,人教A版教材内容栏目设计注重知识的“问题性”,培养学生的问题探究意识;北师大版教材内容栏目设计注重知识的“逻辑性”,让学生深切感知数学源于生活、寓于生活、用于生活;湘教版教材古文式的栏目设计,重在培养学生的学习兴趣,进而促进学生智力因素和非智力因素的发展.
(3)向量内容深度和广度的把握方面.
三版教材中“平面向量及其应用”内容的知识体系挖掘与涉及内容范围有所不同. 其中,内容广度方面,人教A版教材与北师大版教材基本相似,湘教版教材最小;内容深度方面,北师大版教材概念涉及最深,人教A版教材次之,湘教版教材最小. 总的来说,北师大版教材内容设计深度和广度最大,人教A版教材次之,湘教版教材最小.
(4)向量数学文化的渗透方面.
三版教材中“平面向量及其应用”内容的文化引入次数、涉及范围及侧重点均存在差异. 相比而言,人教A版教材在阅读与思考窗口引入“向量及向量符号的由来”和“海伦和秦九韶”的数学文化,注重数学知识的历史性、人文性和应用性;北师大版教材在阅读材料窗口引入“向量的发展历史与符号由来”的数学文化,更侧重数学知识的历史性;湘教版教材未涉及数学文化的引入.
2. 启示
基于三版教材中“平面向量及其应用”内容的知识结构、栏目设计、内容广度与深度、数学文化渗透的比较分析,可得到关于一线教师教学的几点启示.
(1)不断完善向量知识结构是优化教学设计的关键.
向量知识结构是向量知识点之间联系的重要形式,而解析向量知识结构对教师整体把握向量知识内容的体系框架具有重要作用,是优化教学设计的有效路径. 相比而言,三版教材“平面向量及其应用”内容的知识结构设计各具特色. 因此,教師在完善向量的知识结构时,要根据《标准》的基本理念优化向量教学设计,对向量知识点、知识线、知识块、知识群做复合式、立体式的结构化分析,要充分体现向量知识点间的紧密联系及广泛应用,不断促进学生分析问题、解决问题、批判思维、创造思维的发展,进而提高学生的整体思维品质,发展学生的数学学科核心素养.
(2)充分发掘向量栏目功能是提升教学实施效果的有效路径.
教材中不同的栏目设计,承载着不同的教育功能. 比较发现,人教A版教材向量内容的栏目设计注重学生的主体性、体现知识的问题性,凸显了数学的科学价值;北师大版教材向量内容的栏目设计侧重联系实际生活,凸显了数学的应用价值;湘教版教材向量内容的栏目设计重视文化性,凸显了数学的育人价值. 因此,教师在向量教学的过程中,应基于《标准》中关于向量内容的教学实施要求,精心研究向量内容栏目,充分发掘向量内容不同栏目的育人价值,让学生在切身体会向量丰富数学价值内涵的过程中培育其数学学科核心素养,从而提升教师使用向量栏目所达成的教学效果.
(3)科学设计向量内容深度和广度是开展有效教学评价的必要举措.
《标准》明确指出,数学课程要以学生的发展为本,实现人人都能获得良好的数学教育,不同的人在数学上得到不同发展. 其中,科学地设计向量内容深度和广度对学生理解向量知识有着重要作用,它是开展有效教学评价的必要举措. 相比而言,北师大版教材向量内容设计深度和广度最大,人教A版次之,湘教版最小. 鉴于此,教师在开展向量内容的教学评价时,应注意根据学生的兴趣需要、认知特点,以及向量的发展前景适当调整教学内容,科学设计向量内容的深度和广度,让学生在自主探究、理解及应用的过程中获得良好发展.
(4)恰当渗透多元向量数学文化是执行教学目标、反思教学行为的重要依据.
《标准》提出注重数学文化的渗透. 课堂教学是学生学习数学知识的主要途径,而课堂教学中数学文化的恰当渗透有利于学生数学思维的建构,是教师执行教学目标、反思教学行为的重要依据. 通过比较,发现三版教材中向量内容的文化渗透存在差异,若能取长补短,会取得事半功倍的教学效果. 因此,教师在处理向量教学预设和生成的过程中,不仅要传授学生数学知识与技能、过程与方法,还要尽可能地发展学生的情感、态度与价值观,要恰当渗透多元向量数学文化,激发学生的学习兴趣,让学生体会向量知识的发生、发展过程,感受数学家持之以恒进行相关研究的伟大精神.
参考文献:
[1]付钰,张景斌. 中美数学教材三角函数习题的比较研究[J]. 数学教育学报,2018,27(3):14-18.
[2]吕世虎. 高中数学新课程中的向量及其教学[J]. 课程·教材·教法,2006,26(1):47-50.
[3]林丹,胡典顺. 中美高中数学教材的习题比较及启示:以PEP教材与UCSMP教材中平面向量章节为例[J]. 数学教育学报,2015,24(3):63-67.
[4]王列惠. 谈高中数学中增加“向量”内容[J]. 数学通报,1998(12):8-9,12.
[5]王治刚. 平面向量在高中数学中的运用[J]. 中学数学教学参考(下旬),2018(1 / 2):94-95.
[6]中华人民共和国教育部制定. 普通高中数学课程标准(2017年版)[M]. 北京:人民教育出版社,2018.
[7]史宁中,孔凡哲,李淑文. 课程难度模型:我国义务教育几何课程难度的对比[J]. 东北师大学报(哲学社会科学版),2005(6):151-155.
[8]严家丽,孔凡哲,李清. 中美高中数学教材难度特征的比较研究:以《核心数学课程》和人教A版教材为例[J]. 上海教育科研,2014(3):72-75.
[9]代钦. 释数学文化[J]. 数学通报,2013,52(4):1-4.
[10]邵立元. 核心素养背景下对高中数学文化的再思考[J]. 数学教学通讯(下旬),2020(2):47-48.

