有限元方法在幕墙铝板计算中的应用问题

朱东辉

摘要：利用有限元软件ANSYS建模分析了标准四边支撑铝板在荷载作用下的应力和挠度，并与规范给出的公式解析解对比，得出更符合工程实际的边界约束方法;并验证了随着荷载增大，挠度变大，由弯曲引起的板中面的拉伸作用变的不可忽略，需要考虑几何非线性。

关键词：铝板;解析法;有限元法;几何非线性

作为金属幕墙的一种，铝板幕墙具有重量轻、强度高、耐候性能好以及丰富的色泽和肌理等特点，在现代建筑中被广泛使用。在铝板幕墙设计中，建筑立面划分，面板的规格与厚度的选择都取决铝板的计算。四边支撑金属平板的最大应力和最大挠度可根据规范中给出的解析公式计算，而单曲面、双曲面及异形板则宜采用几何非线性的有限元方法计算。

随着计算机技术和计算方法的快速发展，计算机及其结构计算程序在幕墙结构设计中得到大量的应用，为结构设计提供了快速、准确的计算工具[1]。在借助有限元软件进行辅助计算时，应充分考虑模型建立的准确性，与规范公式计算结果对比分析，或者结合实验论证之后谨慎采用。

1、规范解析公式计算方法与适用范围

JGJ 133—2001《金属与石材幕墙工程技术规范》仅给出了四边支撑金属板的强度计算公式，上海地方标准DG/TJ 08-56-2019《建筑幕墙工程技术标准》（以下简称“规范”）在国家标准的基础上，结合工程案例和大量的试验数据，不断的完善和总结，给出了更为完整的规定，可作为普遍计算依据。

上海规范第11.3.6及11.3.7条分别规定了四边支撑面板的最大弯曲应力和面板跨中挠度的计算公式，公式如下：

其中面板的最大应力设计值需要将不同荷载作用下板的最大应力标准值按规范10.4节规定进行组合。其他荷载作用下的最大弯曲应力标准值需要将风荷载标准值wk替换为相应的荷载，例如垂直于面板方向的地震荷载作用下的最大弯曲应力标准值，仅需要将式（1）和式（2）中的风荷载标准值wk替换为水平地震荷载标准值qEk即可。

弹性薄板理论只适用于计算挠度df不大于板厚t的条件。随着挠度和板厚的比值加大，应力和挠度的计算值会偏大较多，偏差到一定程度时应力及挠度控制条件便失去意义。因此，在小挠度理论计算公式基础上，考虑适当的折减系数对计算结果进行修正，以接近实际值。此解析公式便捷高效，具有实际的工程意义。但是适用范围有限，仅适用于四边支撑的金属平板、多边形板（按其外接四边形考虑）以及曲率较小的弧形板。对于较为复杂弧形及异形板则需要采用几何非线性的有限元方法计算。

2 四边简支铝板有限元分析

2.1 不同约束条件下铝板有限元分析

为探讨有限元分析方法在异形复杂金属面板计算的应用，在此对标准四边简支铝板采用有限元软件ANSYS进行建模分析，并将计算结果与规范解析解对比。

计算铝板尺寸为1000mm*600mm，厚度为3mm，铝板牌号为3003，状态为H14，铝合金的弹性模量E=70000MPa，泊松比ν=0.33，承受垂直于面板方向的风荷载为0.001MPa。面板模型网格单元划分最大尺寸为50mm*50mm。建立两种不同的约束条件分别进行线性和几何非线性分析：A——约束四条边x，y，z自由度;B——约束相邻两条边x，y，z自由度，另外两条边仅约束z自由度。

约束条件A小挠度（线性）分析结果：最大应力为18.675MPa;最大挠度为6.327mm。应力及挠度云图如图1、图2所示。

约束条件A大挠度（几何非线性）分析结果：最大应力为10.531MPa;最大挠度为2.624mm。应力及挠度云图如图3、图4所示。

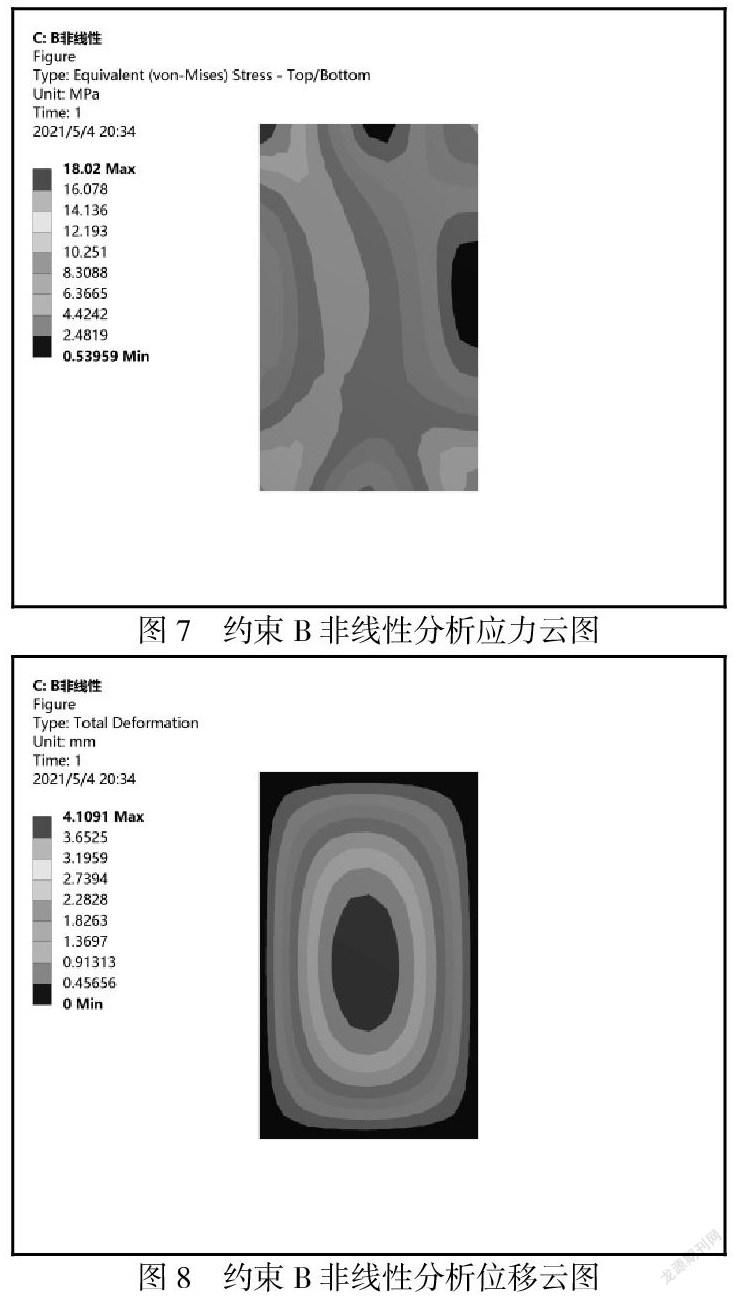
约束条件B小挠度（线性）分析结果：最大应力为18.675MPa;最大挠度为6.327mm。应力及挠度云图如图5、图6所示。

约束条件B大挠度（几何非线性）分析结果：最大应力为18.02MPa;最大挠度为4.109mm。应力及挠度云图如图7、图8所示。

2.2 不同荷载作用下铝板有限元分析

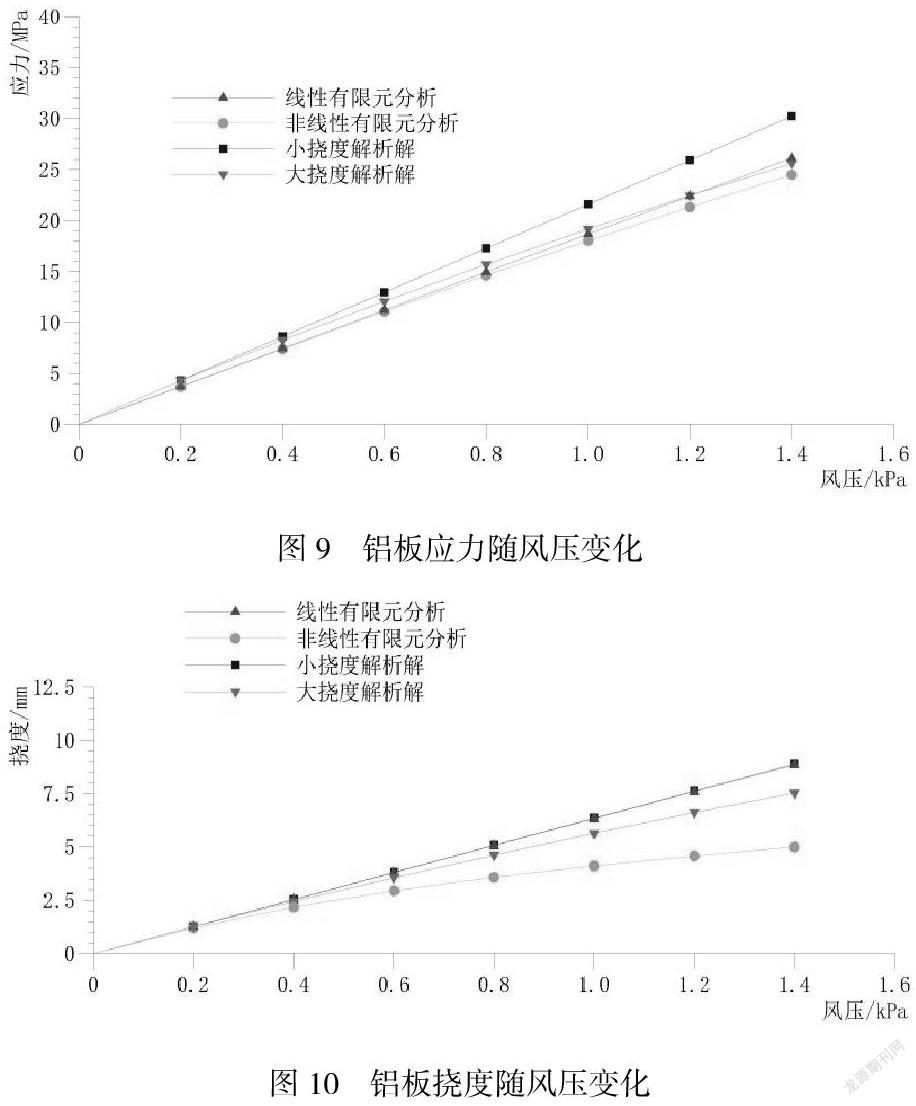
计算铝板尺寸为1000mm*600mm，厚度为3mm，铝板牌号为3003，状态为H14，铝合金的弹性模量E=70000MPa，泊松比ν=0.33，面板模型网格单元划分最大尺寸为50mm*50mm。约束条件为约束相邻两条边x，y，z自由度，另外两条边仅约束z自由度（即2.1节的“约束B”）。承受垂直于面板方向的风荷载取值0.0002MPa、0.0004MPa、0.0006MPa、0.0008MPa、0.001MPa、0.0012MPa、0.0014MPa。按以上荷载取值分别进行线性和非线性有限元分析，求出最大应力即最大挠度。按照规范小挠度和大挠度公式分别计算以上荷载作用下的最大应力和最大挠度。铝板应力和挠度随风压变化计算结果如图9和图10所示。

3 有限元方法计算结果和解析解对比分析

3.1 结果对比

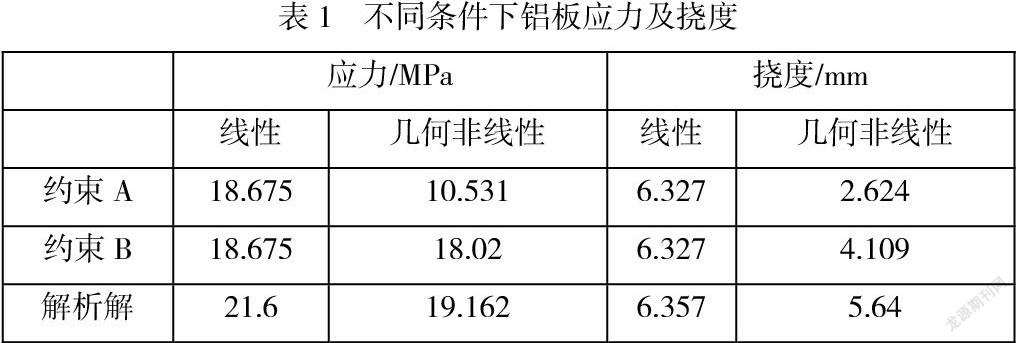
将不同约束条件下采用有限元软件分析的计算结果和DG/TJ 08-56-2019《建筑幕墙工程技术标准》给出的理论公式计算得出解析解汇总之后作对比，见表1。

3.2 结果分析

通过图9和图10可以得出，荷载小于0.4kPa时线性和几何非线性的解比较接近，随着荷载的增大，面板挠度增加直至大于板厚t=3mm，面板大变形的影响变得不可忽略，考虑了几何非线性的计算结果均小于线性解，说明大变形几何非线性计算因考虑了大变形条件下面内薄膜应力的有利影响，使得铝板最大应力和最大挠度均变小，且偏差较大，理论计算结果更接近工程实际，对降低工程成本有利。而在实际工程应用中，铝板的挠度均远大于板厚，必须要考虑大变形的影响进行几何非线性计算。

表1可以得出，“约束A”和“约束B”同样在考虑了几何非线性的条件下应力和挠度明显偏差，是因为后者没有对边界的平面内方向的自由度进行约束。由于工程实际中面板的四条边在平面内方向是有一定的位移能力的（即四边简支），而非如“约束A”中将四条边的三个方向的自由度均进行约束。结果也表明“约束B”条件下的结果与规范给出的经验公式解析解更加吻合，更加符合实际结果，可以作为设计依据。所以工程师在借助有有限元软件进行设计计算时需注意模型边界条件的设定对结果的影响，并将计算结果与规范公式解析解进行对比。对于复杂模型的分析，无法进行公式计算的，应进行模拟试验，或者用其他有限元软件计算结果对比之后采用。

分析所得到的几何非线性有限元计算结果的应力值和挠度值，均小于规范在考虑了大挠度折减系数的解析解，也验证了规范编写时出于安全考虑，给出的计算公式偏安全和保守的原则，但两者结果比较接近，均可用于工程设计。

通过对标准四边简支金属板的有限元模型分析，并与规范公式计算结果对比，总结出相对准确的建模方法，尤其是板边边界的约束方式，应尽量结合工程实际，与面板实际受力情况和支撑方法相吻合。从而将此建模方法延伸应用至更为复杂的曲面板和异形板的有限元分析计算。

4 结论

（1）设计师可依据更为完善的上海地方标准DG/TJ 08-56-2019《建筑幕墙工程技术标准》计算金属面板。但是仅适用于四边支撑的金属平板、多边形板（按其外接四边形考虑）以及曲率较小的弧形板。对于较为复杂弧形及异形板则需要采用几何非线性的有限元方法计算。

（2）在对金属面板进行几何非线性有限元分析时，需要注意所建立模型的受荷形式和边界约束形式与工程实际一致或尽可能一致。才能得到足够精确且符合工程实际的计算结果，其结果方可作为设计依据。否则将会造成材料浪费，增加经济成本，甚至留下严重的安全隐患。

（3）验证了随着荷载不断增大，面板挠度变大，由弯曲引起的板中面的拉伸作用变的不可忽略，需要考虑几何非线性。利用有限元软件分析时，可打开大变形选项，当模型为小变形时得到小变形结果，当模型为大变形时则得到更加准确的计算结果。

参考文献：

[1]桑嘉賓，陶照堂.点支撑鳞片铝板的有限元分析[J].门窗，2017（5）：7～10.

[2]JGJ 133—2001.金属与石材幕墙工程技术规范[S].

[3]DG/TJ 08-56-2019.建筑幕墙工程技术标准[S].

上海昊悉建设发展有限公司 上海 201100