基于对数行列式实现的矩阵补全算法

秦国峰 彭冲 魏计鹏

摘要：传统的基于低秩假设的矩阵补全模型常常对目标矩阵采用核范数的约束，由于核范数对秩函数的近似不够精确，基于核范数的低秩模型可能无法产生最优的效果。为此，采用对数行列式代替核范数，提出基于最小化矩阵对数行列式的矩阵补全模型。研究结果表明，基于最小化对数行列式实现的矩阵补全算法能够有效地恢复矩阵的低秩信息，能够有效地补全图像的缺失信息。

关键词：矩阵补全;低秩结构;对数行列式;机器学习

中图分类号：TP181

文献标志码：A

收稿日期：2020-11-06

通信作者：彭冲，男，博士，副教授，主要研究方向为机器学习。E-mail： Pchong1991@163.com

在现实世界中，数据量变得越来越大，越来越多的数据开始采用矩阵的形式存储。由于存储设备的损坏，网络中信息传输不稳定导致传输过程中数据丢包等原因，出现了大量数据缺失的问题[1]，因此从非常有限的信息中估计缺失值这项技术变得尤为重要。矩阵补全技术被广泛应用在很多领域。例如，图像恢复[2]，视频去噪[3]和推荐系统[4-5]等。在近二十年中，矩阵补全算法得到了长足的发展，其中基于低秩的模型具有显著的性能[6-9]。基于低秩的模型通常对目标矩阵做出一个合理的假设，即目标矩阵是低秩的或近似低秩的，基于此假设，研究人员提出了矩阵补全问题的基础建模[6]。然而，矩阵补全基础模型秩最小化问题很难求解，为了解决这个问题，现有算法通常使用核范数来代替秩函数。理论研究表明核范数是最贴近秩函数的凸下界[10];采用核范数来近似代替秩函数的现有方法有很多，例如奇异值阈值（SVT）[11]，核规范正则最小二乘法（NNLS）[12]和鲁棒性主成分分析（Robust PCA）[13]。研究发现，当矩阵存在较大奇异值时，核范数对矩阵秩的近似往往不够精确，因此在实际应用中可能会获得次优性能[14]。本文针对核范数对于秩函数的拟合不够精确这一问题，提出了改进后的矩阵补全算法。相对于将矩阵所有奇异值直接相加的核范数，本文采用基于矩阵对数行列式的方式近似矩阵的秩，从而有效地减小较大的奇异值对矩阵低秩性质的影响。相比于核范数而言，对数行列式对于秩函数的近似更为精确。因此，本文通过采用对数行列式代替秩函数，得到了新的矩阵补全模型。

1 相关工作介绍

近些年，矩阵补全技术被广泛应用于各种领域，包括机器学习，计算机视觉，信号处理等。最近的研究进展表明，基于核范数的矩阵补全算法对于低秩部分的近似不够精确，针对这个问题本研究考虑采用对数行列式来解决。

1.1 对数行列式

对于任意矩阵X∈Rm×n，矩阵的对数行列式定义为

F（X）=logdet（I+XTX）（1）

显然，logdet（I+XTX）=∑ni=1log（1+σ2i，X），其中，σ1，X>σ2，X>…>σn，X≥0，σi，X是矩阵X的第i个奇异值。

1.2 奇异值阈值算法（SVT）

SVT[11]算法是采用核范数近似代替秩函数从而实现矩阵补全的一种算法，模型为

minXX*+αX2Fs.t. PΩ（X）=PΩ（M）（2）

其中，X∈Rm×n是恢复出的矩阵;M∈Rm×n是给定的低秩的不完整的数据矩阵;α为平衡参数;Ω是一组对应于能被观察到的项目的位置信息。PΩ（X）定义为：当（i，j）∈Ω时，PΩ（X）ij=Xij; 当（i，j）∈Ωc时，PΩ（X）ij=0。

通过使用对数行列式来对函数的低秩部分进行拟合，这种效果要好于核范数的拟合效果，本文采用这种方式成功的解决了核范数作为秩函数近似不够精确的问题[14]。

2 本文方法

2.1 目标函数

考虑到核范数作为矩阵低秩部分的表现不够理想，本文采用对数行列式作为对秩函数的非凸近似

min Xlogdet（I+XTX）s.t. PΩ（X）=PΩ（M）（3）

其中，I为单位阵;M∈Rm×n; X∈Rm×n是修复后的新矩阵。

2.2 模型的优化

由于难以直接优化目标函数，本文通过引入辅助变量来简化模型，从而得到新模型

min logdet（I+XTX）s.t. W=X，PΩ（X）=PΩ（M）（4）

优化阶段，本文采用了ALM（增广拉格朗日法）[15]的优化算法，交替迭代优化每一个变量。给出模型的增广拉格朗日方程式

L=F（X）+ρ2W-X+θρ2F（5）

其中，ρ 是平衡参数，θ 是拉格朗日乘子。

2.2.1 最小化X 关于X的子问题

Xt+1=argminX F（X）+ρt2Wt-X+θtρt2F（6）

其中，t為迭代次数。对于使用对数行列式的子问题，通过文献[14]的证明，可知式（6）等价于求解

σ*i=argminσ*i∑ig（σ*i）+ρt2（σ*i-σi，H）2s.t. σ*i≥0，（i=1，…，n）（7）

其中，g（x）=log（1+x2）; σ*i是所求更新后的最优解X的第i个奇异值，H=Wt+θt/Pt，σi，H≥0，（i=1，…，n）是矩阵H的第i个奇异值。对关于σi的函数f（σi）=log（1+σ2i）+ρt2（σi-σi，H）2分别求一阶导数和二阶导数，得

f′（σi ） = 2σi 1 + σ2i+ ρt （σi -σi，H ）（8）

f''（σi ） = ρt σ4i+ （2ρt -2）σ2i+ （2 + ρt ）（1 + σ2i）2（9）

令f′（σi）=0，得

ρtσ3i-ρtσi，Hσ2i+（ρt+2）σi-ρtσi，H=0（10）

其中，σi≥0，（i=1，…，n）; 矩阵H的SVD是U diag（{σi，H}ni=1）VT; U，V均为单位正交矩阵，且UUT=I，VVT=I，U为左奇异矩阵，V为右奇异矩阵;diag（{σi，H}ni=1）是主对角线元素为σi，H，（i=1，…，n），其余元素为0的主对角矩阵;σi，H≥0，（i=1，…，n）。

本文通过两种情况进行分析。

情况1：如果σi，H=0，由于σi≥0，可知f′（σi）≥0，故f（σi）是非减函数，因此，σi=0时，函数f（σi）最小。

情况2：如果σi，H>0，此时有f′（0）<0，f''（0）>0，因此至少存在一个根∈（0，σi，H）; 当ρt>0.25时，可以看出f''（σi）>0，因此f′（σi）是有唯一全局最优解的凸函数，此时σ*i可以通过f′（σi）=0求解得到。当0<ρt<0.25时，可以通过以下方式进行求解：删掉式（10）求解中负根的集合，获得解集Ο+，根据一阶必要条件定理，可知σ*i=argminσi∈{0}∪Ο+f（σi）。

设置初始化ρt=0.000 1，且ρt随着迭代次数不断增大，在迭代到17次时，满足ρt>0.25，通过这种方式，来保证当σi，H>0时，有σ*i∈（0，σi，H）; 当σi，H=0时，σ*i=0。

综上，得到Xt+1的更新方式为

Xt+1=U diag（σ*1，…，σ*n）VT（11）

2.2.2 最小化W 关于W的子问题为

Wt+1=argminWρt2W-Xt+1+θtρt2F（12）

针对上述最小化问题，通过对式（10）中W求导，得到Wt+1的更新方式为

Wt+1=Xt+1-θtρt（13）

为了保证原图像已知的像素值不变，加入约束条件PΩ（W）=PΩ（M），得到Wt+1的更新方式

Wt+1=PΩc（Wt+1）+PΩ（M）（14）

其中，Ωc是一组对应于矩阵中缺失项的位置信息。

2.2.3 其他变量的更新 关于变量ρ与θ的更新方式为

ρt+1=ρt×k（15）

θt+1=θt+ρt+1（Wt+1-Xt+1）（16）

其中，k>1，保证每次迭代ρ都是增大的。

上述优化算法可以归为算法1。

算法1

输入：需要处理的数据矩阵，以及缺失位置的下标;初始化ρ和θ。

（1） 给定最大的迭代次数matrix，迭代进行优化;

（2） 設置t=1，计算 max{Wt-Xt2F，Xt+1-Xt2F，Wt+1-Wt2F}≤0.001，判断是否收敛;

（3） 根据式（11）计算Xt+1;

（4） 根据式（14）计算Wt+1;

（5） 根据式（15）计算ρt+1，根据式（16）计算θt+1;

（6） 跳转至第二步直到收敛;

（7） Return Xt+1。

3 实验及结果分析

实验采用和SVT[11]算法相同的参数初始值，令ρ=0.000 1。当迭代进行到17次时，ρ>0.25，此时满足实验方法所需条件，可以认为本文算法在前16次的迭代中，提供了满足实验条件的初始化。

3.1 对比方法及实验数据

为保证实验的有效性，选取实验数据时，借鉴文献[16]，选用对比度较为明显的图1～图4，能够更直观的看到对比实验效果。实验设计时，分别进行了25%，50%，75%的随机缺失值处理，并记录缺失值的位置。在对比实验部分，选用经典的SVT（奇异值阈值算法）。

3.2 恢复图像对比

图1～图4，展示了矩阵补全算法的对比实验效果图（原数据图片节选自文献[16]，下载链接为https：//github.com/xueshengke/TNNR）。实验选用随机添加了75%缺失值的噪声图像的矩阵补全效果图作为展示。从图1～图4的对比图展示部分，不难看出，新算法恢复后的图像噪声信息更少，色彩饱和度和局部图像质量更加接近原图像。

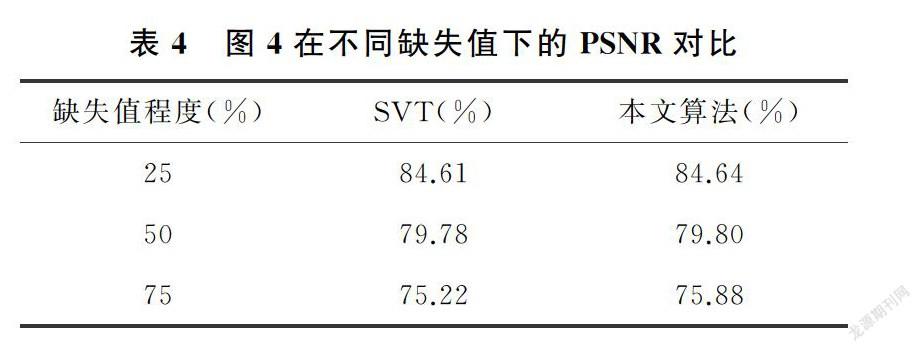
3.3 PSNR值比较

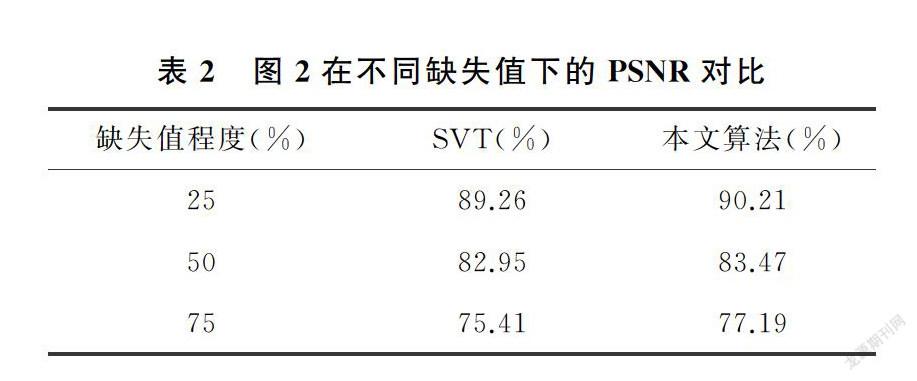
实验中选用PSNR值来衡量恢复后的图像质量，PSNR值越大，表示恢复出的图像质量越好。对三种不同噪声水平的图片，分别用SVT算法和本文的算法分别进行图像恢复，并记录修复后图像的PSNR值，记录在表1～表4中。

从表1～表4展示的实验结果很容易发现，在相同条件下，修复后的图像在PSNR值的对比上，使用本文方法获得的PSNR值较大，矩阵补全效果明显好于经典的SVT算法。实验验证了本文的猜想，相比于SVT算法采用核范数近似秩函数的做法，采用对数行列式的方式，能够更好的作为秩函数的近似，充分利用了数据矩阵的低秩性质，提高了矩阵恢复的效果。

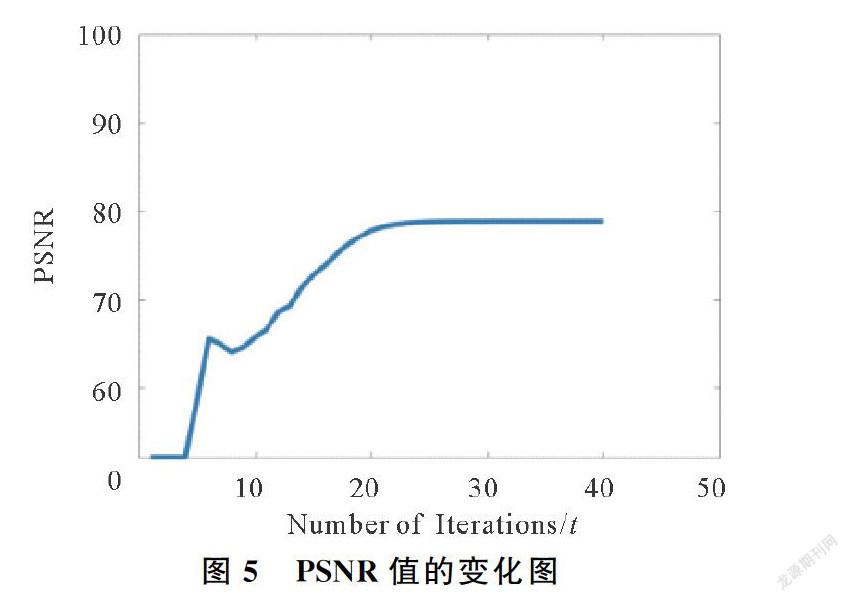
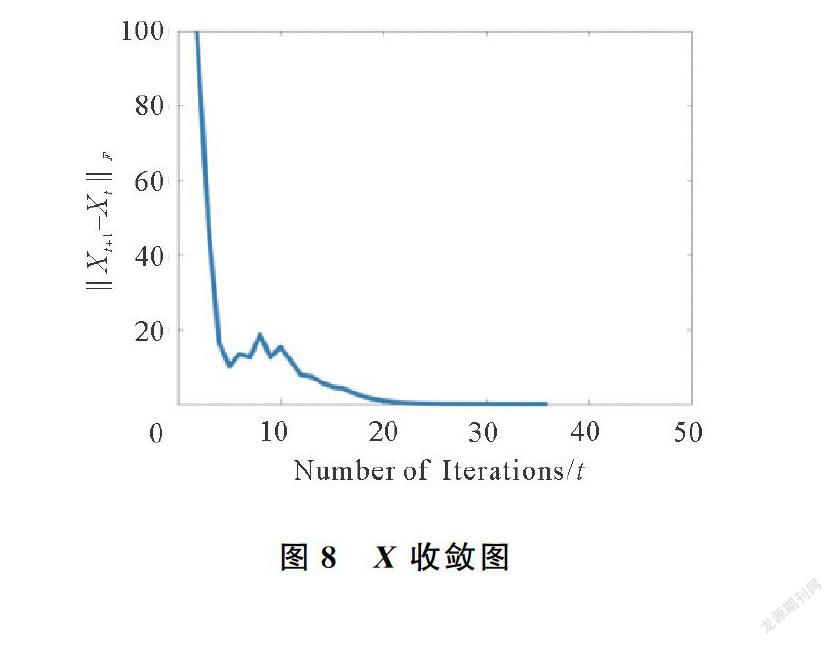
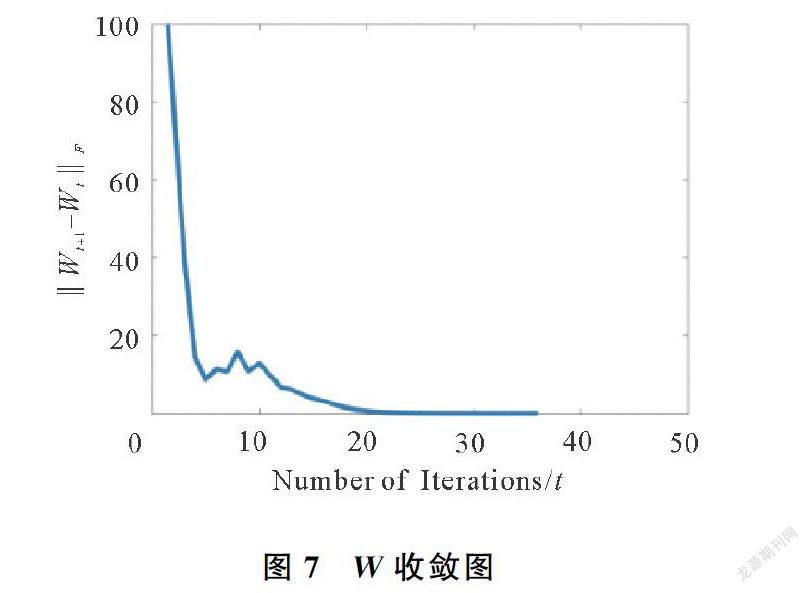
3.4 收敛性分析

为了测试本文方法的收敛性，实验设计中本文针对图1分别计算了每次迭代中的PSNR值，W-X2F，Xt+1-Xt2F，以及Wt+1-Wt2F的值，收敛图分别如图5～图8所示。可知，在迭代40次左右，模型已经收敛。

4 结论

本文提出了一种新的矩阵补全算法的模型。在目标函数低秩性部分改进了核范数替代秩函数不够精确的问题，采用对数行列式代替核范数作为秩函数的近似。在实验优化部分，本文采用ALM的优化方式对模型进行优化，解决了非凸问题优化困难的技术难点。在所设计的图像补全实验中，本文算法表现良好，证明了其有效性。

参考文献

[1]王兴宏.大数据应用及新时期所面临的挑战研究[J].青岛大学学报（自然科学版），2020，33（3）：22-27.

[2]NIKOS K. Image completion using global optimization[C]//Computer Vision and Pattern Recognition. New York， 2006： 442-452.

[3]JI H， LIU C， SHEN Z， et al. Robust video denoising using low rank matrix completion[C]// 23rd IEEE Conference on Computer Vision and Pattern Recognition， CVPR. San Francisco， 2010： 13-18.

[4]STECK H. Training and testing of recommender systems on data missing not at random[C]//Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Washington， 2010，713-722.

[5]KANG Z， PENG C， CHENG Q. Top-N recommender system via matrix completion[C]// 30th Association for the Advancement of Artificial Intelligence （AAAI） Conference on Artificial Intelligence. Phoenix， 2016，179-184.

[6]CANDES E J， RECHT B. Exact matrix completion via convex optimization[J]. Computational Math， 2009， 9： 717-772.

[7]CANDES E J， TAO T. The power of convex relaxation： Near-optimal matrix completion[J]. IEEE Transactions on Information Theory， 2010， 56（5）：2053-2080.

[8]LIU J， MUSIALSKI P， WONKA P， et al. Tensor completion for estimating missing values in visual data[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2013， 35（1）：208-220.

[9]ERIKSSON A， HENGEL A V D. Efficient computation of robust low-rank matrix approximations in the presence of missing data using the L1 Norm[C]//2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco， 2010： 771-778.

[10] RECHT B， FAZEL M， PARRILO P A. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization[J]. Siam Review， 2010， 52（3）：471-501.

[11] CAI J， CAND E J， SHEN Z. A singular value thresholding algorithm for matrix completion[J]. Siam Journal on Optimization， 2008， 20（4）：1956-1982.

[12] TOH K C， YUN S. An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems[J]. Pacific Journal of Optimization， 2010， 6（3）：615-640.

[13] PENG C， CHEN Y， KANG Z， et al. Robust principal component analysis： A factorization-based approach with linear complexity[J]. Information Sciences， 2019， 513： 581-599.

[14] PENG C， KANG Z， LI H， et al. Subspace clustering using log-determinant rank approximation[C]//Proceedings of the 21th ACM SIGKDD international conference on Knowledge Discovery and Data Ming.Sydney，2015：925-934.

[15] YANG J， YUAN X. Linearized augmented lagrangian and alternating direction methods for nuclear norm minimization[J]. Mathematics of Computation， 2012， 82（281）：301-329.

[16] HU Y， ZHANG D B， YE J P， et al. Fast and accurate matrix completion via truncated nuclear norm regularization[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence， 2013， 35（9）：2117-2130.

Matrix Completion Algorithm Based On Log-determinant

QIN Guo-feng， PENG Chong， WEI Ji-peng

（College of Computer Science and Technology， Qingdao University， Qingdao 266071， China）

Abstract：

The nuclear norm constraint is mainly used for the target matrix in traditional matrix completion models based on low-rank assumptions. However， the nuclear norm is not accurate enough to approximate the rank function. Thus it may lead to degraded performance in low-rank recovery problem. To resolve the drawback of the nuclear norm in low-rank recovery， the log-determinant is used to replace nuclear norm and the matrix completion model based on the log-determinant minimization is proposed. Experimental results show that proposed method can effectively recover the low-rank structure of the target matrix and complete the missing entries of corrupted images in image completion application.

Keywords：

matrix completion; low-rank structure; log-determinant; machine learning