基于物元分析法的石材可锯性分级

栾利强 白硕玮 王继荣 王秋燕 刘婷 周琪

摘要：针对企业难以依据石材可锯性选择加工方案和设备造成的能源浪费问题，提出了一种石材可锯性评价方法，综合考虑影响石材可锯性分级的特性指标，建立了可锯性评价指标体系。采用随机森林算法（Random Forest，RF）对石材可锯性评价指标进行赋权，基于物元分析法评定石材的可锯性等级。研究结果表明，通过RF确定指标权重可以减少主观赋权的影响;利用物元分析法综合评价石材可锯性，确定企业加工石材的可锯性为0.042，容易等级，可为企业进行石材加工提供参考依据。

关键词：石材;可锯性;随机森林;物元分析法

中图分类号：TH12;TH16

文献标志码：A

收稿日期：2020-09-18

基金项目：

国家自然科学基金（批准号：71701109，51705269）资助;山东省自然科学基金（批准号：ZR2017BG003）资助。

通信作者：

白硕玮，男，博士，副教授，主要研究方向为绿色制造与清洁生产技术、石材加工工艺技术与装备。E-mail： baishuowei1@163.com

近年来石材产业迅速发展，天然石材广泛应用于建筑装饰、精密仪器以及高端机床等领域。不同种类天然石材的成分、粒度、结构、成因等不同，锯切难易程度存在差异，即石材可锯性存在差异[1]。石材可锯性研究能够为石材企业合理设计生产工艺流程、选择加工设备和刀具、预算生产成本等方面提供依据，推动石材行业快速发展。石材可锯性评价方法研究一直是石材加工领域研究的重点和热点，已有众多学者采用不同的方法从不同的角度对石材可锯性进行评价。Tutmez等[2-6]采用了不同的方法建立了石材可锯性评价模型和预测方程，以板材生产率、加工速率、锯片磨损率等对石材可锯性进行评价，Kahraman等[7-10]测定了石材的硬度、强度、Schmidt锤击值以及脆性等指标，利用石材自身的物理和机械特性对其进行可锯性评价。为了简化测量和采集数据的过程，便于石材加工企业快速高效地进行石材可锯性评价，Hoseinie[11]指出石材的单轴抗压强度与硬度能够很好地反映石材的可锯性。Schmiazek[12]在研究中表明石材可锯性与Schmiazek磨损因子有很强的相关性。石材的可锯性还与石材弹性极限高低有很强的相关性，杨氏模量能够很好地反映石材弹性极限。可锯性评价需要综合考虑各评价指标对石材可锯性的影响，指标赋权可以确定各评价指标对石材可锯性的重要程度。目前的石材可锯性评价方法通常采用主观赋权法对指标进行赋权，权重评价结果在很大程度上受专家个人主观因素的影响。Breiman在2001年提出了RF[13]。杨凯等[14-16]在研究中都采用了RF对指标进行赋权，表明RF能够有效地对指标进行赋权。区别与以往采用锯切速率、板材生产率、锯片磨损率等间接指标评价石材可锯性，本文以石材自身特性单轴抗压强度（U）、Schmiazek耐磨因子（S）、莫氏硬度（M）和杨氏模量（Y）评价石材可锯性。本文结合石材自身特性和企业实际情况，综合考虑石材的矿物特性、物理特性和机械特性等指标，建立了石材可锯性评价指标体系。同时，采用RF从实际收集的石材可锯性评价指标数据中得到评价指标的权重，利用物元分析法定量评价石材可锯性，对石材可锯性进行表征。

1 石材可锯性评价指标体系

为了对石材可锯性进行全面评价，需要综合考虑石材的矿物特性、物理特性和机械特性等特性指标;同时，为便于石材加工企业在工程应用中测量和采集数据，建立如表1所示的石材可锯性评价指标体系。

2 随机森林算法确定石材可锯性评价指标权重

为了减少评价结果的主观性，采用随机森林算法（Random Forest，RF）对石材可锯性评价指标进行赋权。RF具有极强的数据分析能力且不会出现过拟合现象，对噪声和异常值有很强的容忍度，在进行数据分析的同时可以给出变量的重要性，可以对评价指标进行赋权。

2.1 随机森林的基本原理

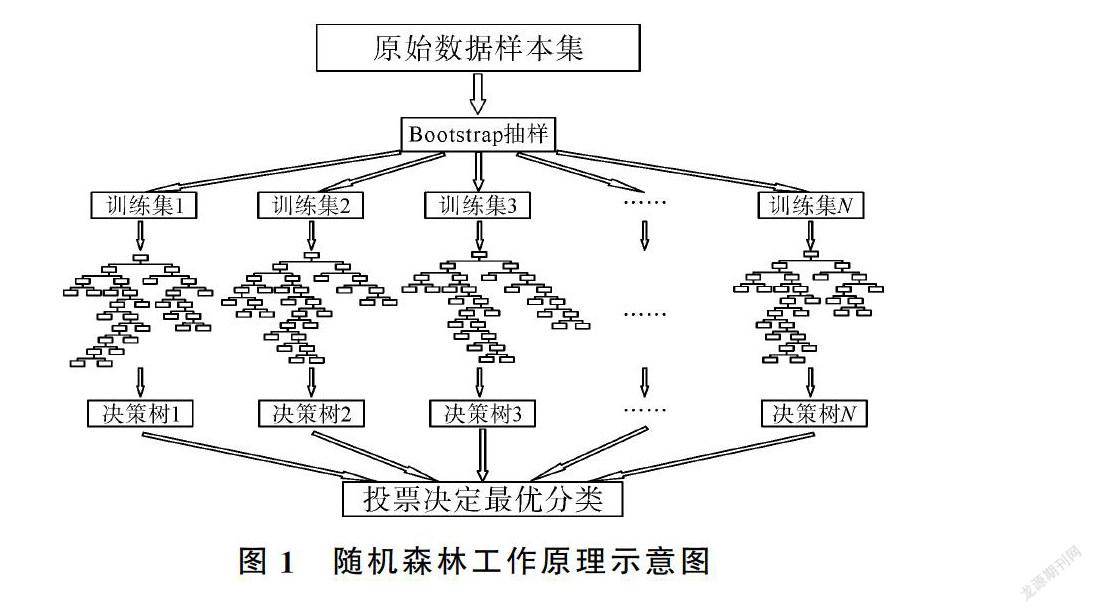
RF是一种基于决策树的组合分类算法，主要用于分类和回归。本研究是用于对石材进行分类，通过Bootstrap重采样技术从原始数据样本集D中有放回地随机抽取N个数据样本生成训练数据样本集E，且每个训练集数据样本容量都与原始数据集样本相同，然后利用训练集数据样本建立N棵决策树组成RF模型。新数据的分类结果由RF模型中决策树进行投票表决确定，具体过程如图1所示。

2.2 随机森林求指标权重方法

随机森林通过“不纯度（impurity）”选择最优的划分指标进行决策树分割，计算数据集中不纯度最常用的方法就是Gini指数。对于数据集E，假设有T个分类，样本属于第t类的概率为pt，则此概率分布的Gini指数为

Gini（p） = ∑Tt = 1pt （1-pt ） = 1-∑Tt = 1p2t （1）

对于训练集E，其Gini指数为

Gini（E）=1-∑Tt=1（BtE）2（2）

其中，Bt表示训练集E中属于第t类的样本个数，E表示训练集E所含样本的总个数。若此时根据指标C将训练集E分裂成两个独立子集E1和E2，则此时训练集E的Gini指数为

Gini（E，C）=E1EGini（E1）+E2EGini（E2）（3）

其中，E1和E2分别表示子集E1和E2中所包含的样本个数。

指标C在该节点的Gini指数变化量为

Giniv=Gini（E）-Gini（E，C）（4）

现假设有指标C1、C2、…、Ci，需要分别计算i個指标在RF所有决策树中的平均Gini指数变化量Ginivi。Ginivi表示指标Ci在RF模型中的重要性。

指标Ci在节点l的重要性，即集合在节点l分裂前后Gini指数变化量为

Ginivil=Gini（H）-Gini（H，Ci）（5）

其中，H为样本数据集在节点l的集合。

假设指标Ci在第n棵树共出现L次，则指标Ci在第n棵树的重要性为

Ginivin=∑Ll=1Ginivil（6）

指标Ci在RF模型中的重要性为

Ginivi=1N∑Nn=1Ginivin（7）

归一化得到指标Ci的权重wi

wi=Ginivi∑ii=1Ginivi（8）

2.3 Python实现随机森林求指标权重

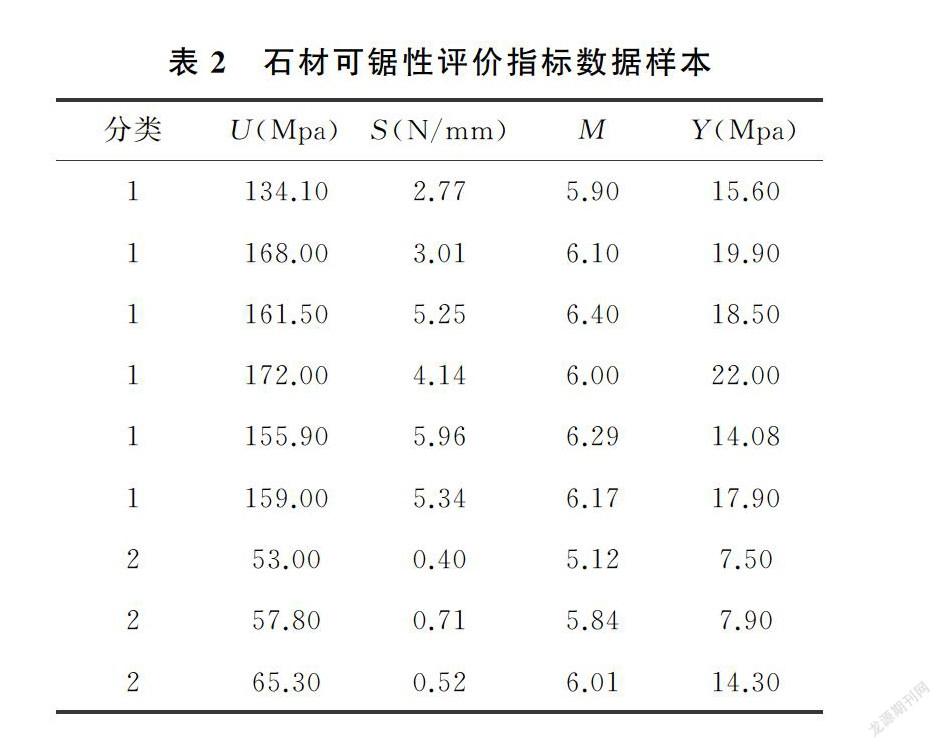
为了获得石材可锯性评价指标的权重，从石材加工企业共采集了268份石材可鋸性评价指标数据样本作为随机森林算法的原始数据样本集D，并整理成RF程序需要的样本集合，表2列出了采集的部分原始数据样本。采用Python编程实现随机森林算法，求得指标权重。将整理好的268份样本数据输入程序，运行程序得到石材可锯性评价指标权重：[wU，wS，wM，wY]=[0.2583，0.2498，0.2449，0.2470]。

3 基于物元分析的石材可锯性评价

石材可锯性评价对石材行业推进绿色清洁生产具有重要意义。目前石材可锯性评价的方法主要有模糊综合评价法、TOPSIS、人工神经网络等[17-18]。石材可锯性本身是一个抽象的概念，由石材可锯性评价指标体系可知，石材可锯性是受多指标共同影响，运用物元分析法可以建立石材多指标参数的定量评价模型，以定量的数值表示石材可锯性，达到评价石材可锯性的目的[19-21]。

物元分析法是以评价事物Q、评价指标C和指标的量值X构成有序三元组R=[Q C X]作为描述评价事物的基本元，简称物元。物元分析法的主要过程为：（1）确定待评对象的经典物元和节域物元;（2）建立关联函数，计算关联函数值;（3）确定评价指标权重;（4）关联度及评定等级。

3.1 确定石材可锯性的经典物元矩阵和节域矩阵

记要评价的对象，石材可锯性为Q，石材可锯性指标记为C，将指标的量值记为X，把“对象、指标、量值”这些要素组成的有序三元组作为评价石材可锯性的基本元，简称物元，即R=[Q C X]

R=Q C X=QC1x1C2x2……Cixi（9）

其中，C=（C1，C2，…，Ci）为评价对象的指标;X=（x1，x2，…，xi）为评价对象对应指标的量值，即待评价对象Q的第i项指标的原始数据。

经典域物元矩阵

Rj=Qj C1 xj1 C2 xj2…… Ci xji=Qj C1 aj1，bj1 C2 aj2，bj2…… Ci aji，bji（10）

节域物元矩阵

Rp=Qp C1 xp1 C2 xp2…… Ci xpi=Qp C1 ap1，bp1 C2 ap2，bp2…… Ci api，bpi（11）

3.2 建立关联函数

关联函数表示当物元的量值取为实轴上的一点时，物元符合所要求的取值范围的程度。根据可拓集合理论，建立关联函数

Kj（xi）=-ρ（xi，Dji）Dji，xi∈Djiρ（xi，Dji）ρ（xi，Dpi）-ρ（xi，Dji），xiDji （12）

其中，Dji=aji-bji，ρ（xi，Xji）=xi-12（aji+bji）-12（bji-aji），ρ（xi，Dpi）=xi-12（api+bpi）-12（bpi-api），xi为评价对象对应指标的量值，即待评价对象Q的第i项指标的原始数据。

3.3 确定评价指标权重及评定等级

根据式（8）确定评价指标权重，由每个指标Ci的关联函数Kj（xi）及每个指标的权重wi，可确定待评价对象Q对于各等级j的综合关联度

Kj（Q）=∑ii=1wiKj（xi）（14）

待评价对象的隶属度函数为：[K1（Q），K2（Q），…，Kj（Q）]，则待评价对象Q的隶属等级为：Qj=maxKj（Q）。

4 实例分析

山东日照某石材加工厂需要根据石材A的可锯性选择合适的加工方案和锯片进行锯切加工，达到节约能源、降低成本、提高产品质量的目的。石材A为花岗岩，用于生产板材。基于国际岩石力学学会（International society of rock mechanics，ISRM）建议的石材评价指标值室内测试方法进行测定，测得待评价石材A的可锯性评价指标值为：[U，S，M，Y]=[116，2.36，5.49，13.66]。

4.1 确定石材可锯性的经典物元矩阵和节域矩阵

根据石材行业标准以及收集的石材可锯性评价指标数据样本，通过咨询行业专家，将石材可锯性评价等级Qj划分为非常容易、很容易、较容易、容易、稍微容易、一般、差、较差、很差、非常差十个等级。对于各指标在十个等级中的取值范围主要依据各指标在该变化范围内对石材可锯性影响程度不同进行划分，得到如表3所示的标准分级。

石材可锯性评价的节域物元矩阵：

Rp=Qp U 53，173 S 0.4，5.96 Q 5.12，6.4 Y 7.5，22

4.2 建立关联函数

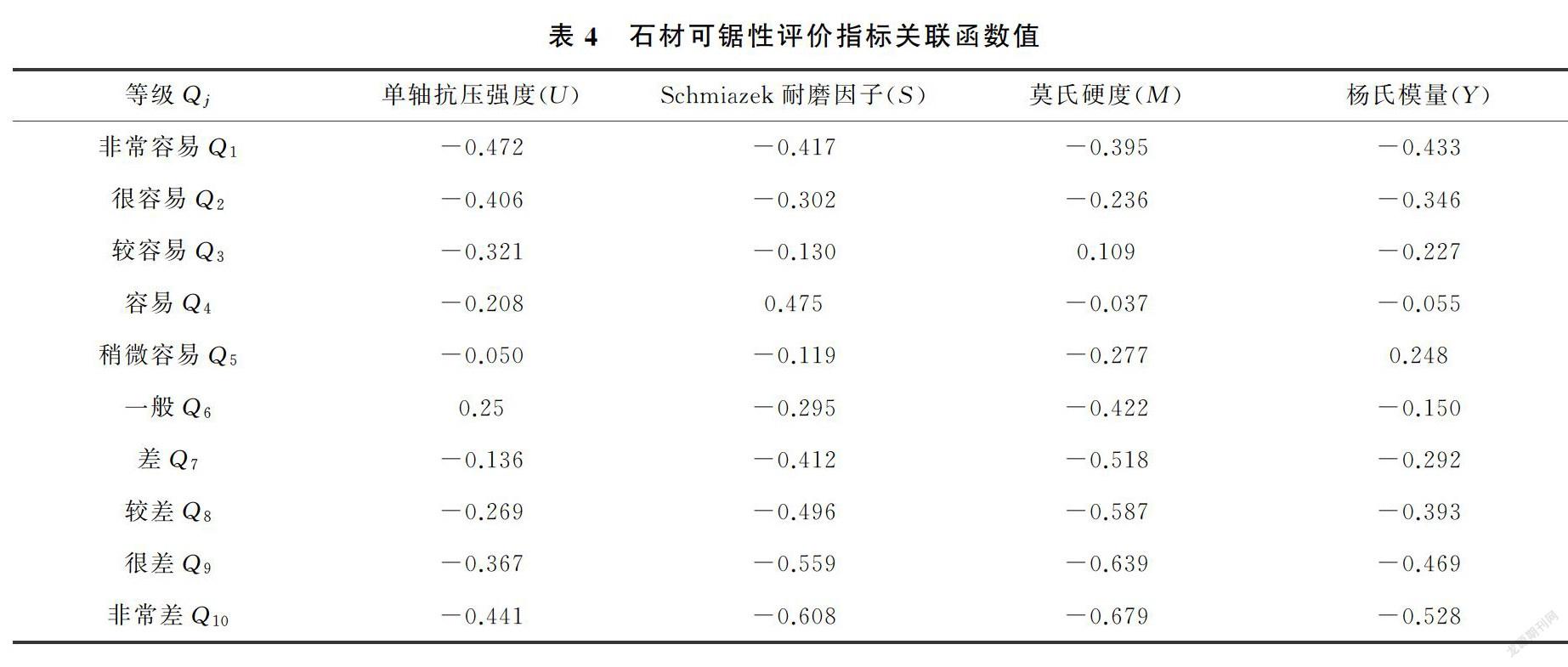
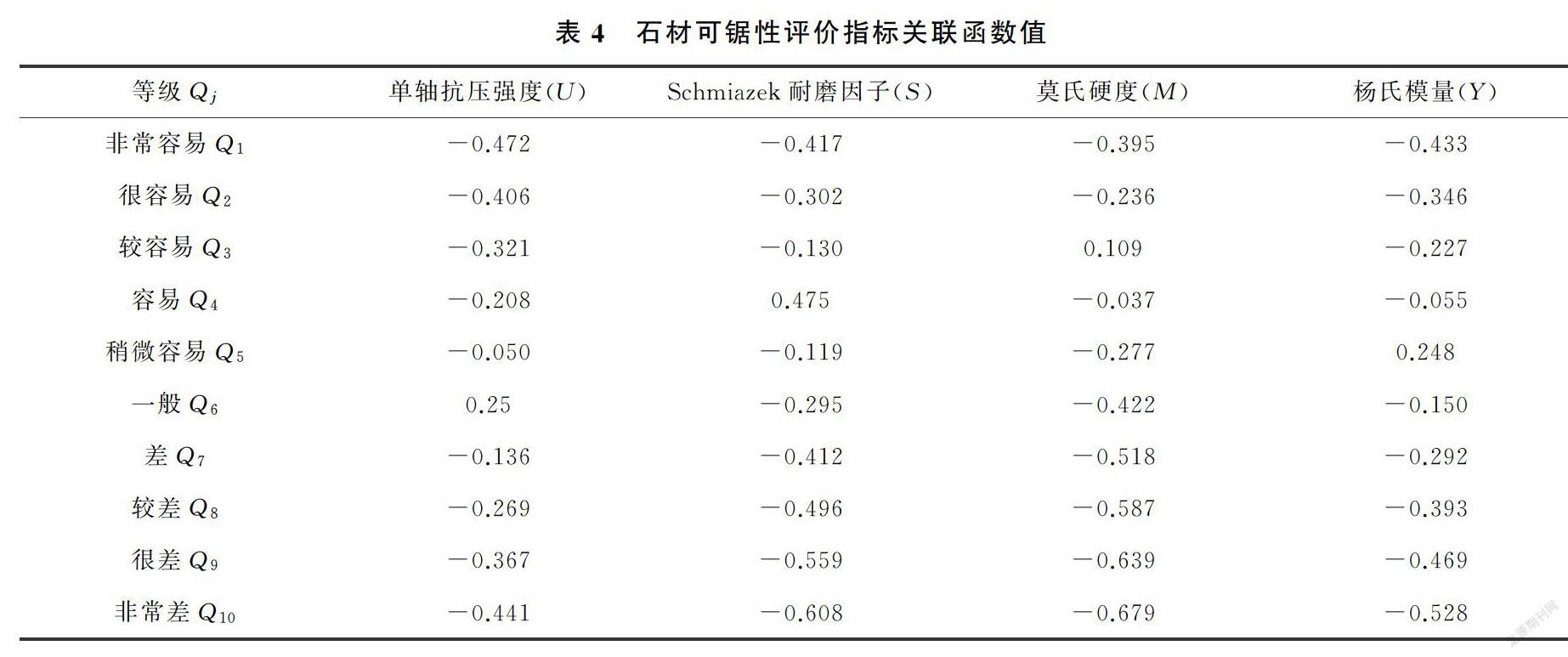
根据经典物元矩阵和节域矩阵，将指标的量值[U，S，Q，Y]=[116，2.36，5.49，13.66]带入到式（12）能够计算出待评价石材的关联函数值，如表4所示。

4.3 确定评价指标权重

利用Python编写RF算法程序，从收集的268份石材可锯性评价指标数据样本中得到评价指标的权重为 [wU，wS，wM，wY]=[0.2583，0.2498，0.2449，0.2470]。

4.4 关联度及评定等级

根据式（14），由每个评价指标的关联函数[Kj（U）、Kj（S）、Kj（M）、Kj（Y）]及每个指标的权重[wU，wS，wM，wY]，可确定待评价石材A对于各等级j的综合关联度： [K1（A），K2（A），K3（A），K4（A），K5（A），K6（A），K7（A），K8（A），K9（A），K10（A）]=[-0.430，-0.324，-0.145，0.042，-0.049，-0.150，-0.337，-0.434，-0.507，-0.562]。则石材A的可锯性等级为：Qj=max{Kj（A）}=K4（A）=0.042，所以石材A的可锯性等级为：容易。据此石材加工企业可选择合适的加工方案和锯片對石材A进行锯切加工。

5 结论

本文提出了一种评价石材可锯性的方法。通过从石材加工企业采集可锯性评价指标数据样本，利用RF算法求得评价指标的权重，消除了赋权时主观因素的影响，更加符合石材可锯性的实际情况。采用物元分析法评价石材可锯性可以综合考虑对石材可锯性有影响的指标，能够以定量的数值来评价石材可锯性，划分石材可锯性的等级，完整地反映了石材可锯性。通过实例研究表明此方法能够为石材加工企业选择合理的加工方案和刀具提供依据，同时降低企业成本，提高产品竞争力。

参考文献

[1]隆威. 岩石可锯性分级方法研究[J]. 金刚石与磨料磨具工程， 2000（3）：22-23.

[2]TUTMEZ B， KAHRAMAN S， GUNAYDIN O. Multifactorial fuzzy approach to the sawability classification of building stones[J]. Construction and Building Materials， 2007， 21（8）：1672-1679.

[3]TUMAC D. Artificial neural network application to predict the sawability performance of large diameter circular saws[J]. Measurement， 2016， 80：12-20.

[4]MIKAEIL R， OZCELIK Y， YOUSEFI R， et al. Ranking the sawability of ornamental stone using fuzzy delphi and multi-criteria decision-making techniques[J]. International Journal of Rock Mechanics and Mining Sciences， 2013， 58：118-126.

[5]GUNAYDDIN O， KAHRAMAN S， FENER M. Sawability prediction of carbonate rocks from brittleness indexes[J]. Journal- South African Institute of Mining and Metallurgy， 2004， 104（4）：239-243.

[6]FENER M， KAHRAMAN S， OZDER M O. Performance prediction of circular diamond saws from mechanical rock properties in cutting carbonate rocks[J]. Rock Mechanics & Rock Engineering， 2007， 40（5）：505-517.

[7]KAHRAMAN S， GUNAYDIN O. Indentation hardness test to estimate the sawability of carbonate rocks[J]. Bulletin of Engineering Geology & the Environment， 2008， 67（4）：507-511.

[8]BAYRAM F. Prediction of sawing performance based on index properties of rocks[J]. Arabian Journal of Geosciences， 2013， 6（11）：4357-4362.

[9]GUNEY A. Performance prediction of large-diameter circular saws based on surface hardness tests for mugla （Turkey） Marbles[J]. Rock Mechanics & Rock Engineering， 2011， 44（3）：357-366.

[10] DELGADO N S， RODRIGUEZ-REY A， SUAREZ DEL RI L M， et al. The influence of rock microhardness on the sawability of Pink Porrino granite （Spain）[J]. International Journal of Rock Mechanics & Mining Sciences， 2005， 42（1）：161-166.

[11] HOSEINIE S H， ATAEI M， OSANLOO M. A new classification system for evaluating rock penetrability[J]. International Journal of Rock Mechanics & Mining Sciences， 2009， 46（8）：1329-1340.

[12] SCHMIAZEK J， KNATZ H， The influence of rock structure on the cutting speed and pick wear of heading machines[J]， Glackauf，1970 （106）：274-278.

[13] BREIMAN L. Random Forests[J]. Machine Learning， 2001， 45（1）：5-32.

[14] 楊凯， 侯艳， 李康. 随机森林变量重要性评分及其研究进展[EB/OL]. 北京：中国科技论文在线， 2015.[2020-09-18].http：//www. paper.edu.cn/html/releasepaper/2015/07/212.

[15] LIOU J J H， CHUANG Y C， ZAVADSKAS E K， et al. Data-driven hybrid multiple attribute decision-making model for green supplier evaluation and performance improvement[J]. Journal of Cleaner Production， 2019， 241（20）：118321.1-118321.12.

[16] 吴孝情， 赖成光， 陈晓宏，等. 基于随机森林权重的滑坡危险性评价：以东江流域为例[J]. 自然灾害学报， 2017（5）：119-129.

[17] 田贵全. 大气环境质量评价的判别分析法[J]. 环境科学研究， 1996， 9（3）：45-48.

[18] 何逢标. 综合评价方法MATLAB实现[M]. 北京：中国社会科学出版社， 2010.

[19] 蔡文. 可拓论及其应用[J]. 科学通报， 1999（7）：673-682.

[20] 蔡文.物元模型及应用[M].北京：科学技术文献出版社，1994.

[21] 门宝辉， 梁川. 水质量评价的物元分析法[J]. 哈尔滨工业大学学报， 2003， （3）：358-361.

The Stone Materials Sawability Evaluation Based on Matter Element Method

LUAN Li-qiang， BAI Shuo-wei， WANG Ji-rong，

WANG Qiu-yan， LIU Ting， ZHOU Qi

（School of Electromechanic Engineering， Qingdao University， Qingdao 266071， China）

Abstract：

Aiming at the problem of energy waste caused by enterprises' difficulty in selecting processing schemes and equipment according to stone sawability， a stone sawability evaluation method was put forward， and a stone sawability evaluation index system was established by comprehensively considering the characteristics of stone sawability classification. The weights of the evaluation indexes were obtained by Random Forest（RF） algorithm. The stone sawability grade was evaluated based on mattering element analysis method. The results show that the influence of subjective weighting can be reduced by determining the index weight through RF. The stone sawability is evaluated comprehensively by the matter element analysis method， and the stone sawability is determined to be 0.042 and easy grade in the stone enterprises， which can provide reference for the processing of stone by enterprises.

Keywords：

stone materials;sawability;Random Forest;matter-element analysis method