探析类比法在高中数学教学中的应用

摘 要:解题方法教学是一线教师关注的焦点,在高中数学解题教学中,类比法是典型的解题方法之一,从高中数学解题教学实践来看,类比法的灵活运用是高效解题的关键;本文以高中数学解题教学为探究载体,重点探讨类比法在高中数学的“立体几何、数列、向量、圆锥曲线”等几个方面的运用,以飨读者.
关键词:高中数学;课堂教学;类比法;应用
中图分类号:G632 文献标识码:A 文章编号:1008-0333(2021)12-0002-02
收稿日期:2021-01-25
作者簡介:陈莉(1983.11-),硕士,中学一级教师,从事高中数学教学研究.
高中数学涵盖很多的知识点,需要学生深入理解.教学中注重类比法的应用,结合学生熟悉的知识、情境,进行针对性的引导,使学生正确合理的类比,不仅能很好的加深学生印象,而且有助于学生更好的把握数学知识本质,促进高中数学课堂教学效率的明显提升.
一、类比法用于立体几何教学立体几何是高中数学的重要内容,涉及较多的概念与结论,对学生的记忆以及空间想象能力要求较高.教学中为帮助学生更加清晰的认识立体几何中点、线、面的空间关系,掌握相关的规律,在解题中灵活应用,应做好充分的教学准备,注重类比法的有效应用.
首先,注重概念的类比.讲解立体几何相关概念时应与学生一起回顾平面几何知识,如平面几何中的边、角与角平分线、圆等.同时,借助多媒体技术为学生展示相关的立体几何图形,启发学生进行类比,使学生对相关的概念有个全面的理解.如可将立体几何中的面类比为平面几何中的边、将二面角及角平分面类比角与角平分线、将球类比圆等.如此既能很好的激发学生的学习兴趣,又能使学生更加清晰的认识平面几何与立体几何之间的内在关联.其次,注重性质的类比.立体几何图形的性质是高中教学的重要内容,是各类测试以及高考的考查重点,教学中为使学生更好的掌握与理解不同立体几何的性质,应结合学生已有的知识储备,引导学生进行合理的类比,降低学习难度,提高学习效率.如在圆中经过切点且垂直于切线的直线必经过圆心,以此可类比出球的相关性质,即,在球中经过切点且垂直于切面的直线必经过球心.在课堂上可给学生留下专门的时间,要求学生尝试着进行类比,总结相关立体几何图形的性质.最后,注重结论的类比.立体几何图形中有很多的结论,解题中注重一些结论的应用可获得事半功倍的解题效果,促进学生学习能力的显著提升,因此教学中应引导学生回顾所学的平面几何结论,类比出立体几何中的结论.
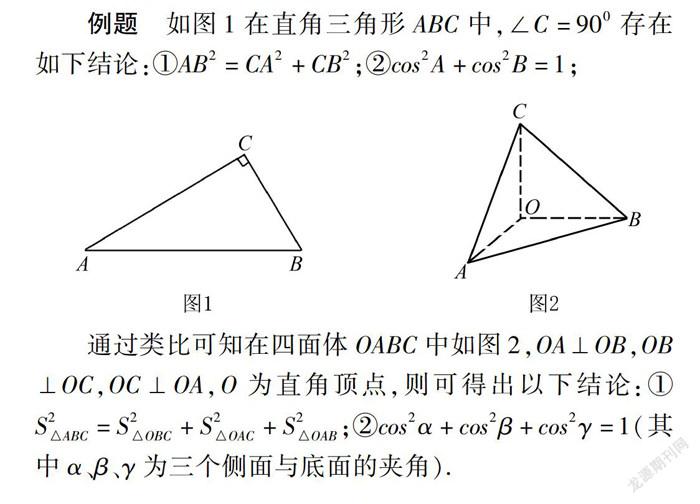
例题 如图1在直角三角形ABC中,∠C=900存在如下结论:①AB2=CA2+CB2;②cos2A+cos2B=1;
通过类比可知在四面体OABC中如图2,OA⊥OB,OB⊥OC,OC⊥OA,O为直角顶点,则可得出以下结论:①S2△ABC=S2△OBC+S2△OAC+S2△OAB;②cos2α+cos2β+cos2γ=1(其中α、β、γ为三个侧面与底面的夹角).
二、类比法用于等比数列教学
高中阶段主要学习等差、等比数列,其中学生最先学习等差数列,包括等差数列的概念、性质等.当学生掌握等差数列相关知识时,在进行等比数列教学时可运用类比法开展教学活动,降低学生学习的陌生感,增强其学习等比数列的自信心.运用类比法时应注重以下内容的落实.
其一,鼓励学生开展自主学习活动.在进行等比数列教学时可结合具体教学内容,给学生预留合理的自主学习时间,要求学生开展自主学习活动.在学习过程中要求学生积极联系所学的等差数列知识进行合理的类比.同时,注重与学生积极沟通,了解学生自主学习情况,针对学生类比过程中存在的问题,给予针对性的指引,保证其类比的正确性,提高自主学习质量.如在讲解等比数列概念时,可要求学生回顾所学的等差数列概念,尝试着总结等比数列概念,以更好的加深学生印象.同时,通过指引使学生认识到等比数列的首项、公比均不能为零.
其二,结合学生表现给予表扬.运用类比法进行等比数列教学时为提高学生的学习体验,应注重结合学生的表现给予针对性的表扬,使其尝到学习的成就感.如在进行等比数列性质教学中,可要求学生结合等差数列中“an=am+(n-m)d”这一性质,通过类比推导等比数列的类似性质,一些学生积极动脑,得出在等比数列中存在的性质为“an=am·qn-m”,显然类比出的这一性质是正确的.课堂上及时表扬这些学生,使其继续保持认真学习、积极思考的态度.
其三,借助类比法提升探究能力.教学中发现等比数列的一些习题较为新颖,对学生的探究能力要求较高.教学中为提高学生的探究能力应注重创设新型的问题情景,要求学生进行类比推理,积累探究的经验与技巧,更好的解答类似的探究问题. 三、类比法用于向量教学向量在高中数学中占有重要地位,知识点多而零碎,对学生的记忆力要求较高.向量知识应用广泛,可作为解答其他数学习题的重要工具.教学中为使学生牢固掌握向量知识,并能在解题中灵活应用,为学生数学学习成绩的提升奠定坚实基础,应注重类比法在教学中的应用.
一方面,讲解向量相关概念时,为使学生更好的理解,应注重引导学生联系所学的实数知识,进行正确的类比.如在讲解向量的模这一概念时,可使学生将其与实数的绝对值进行类比.通过类比学生能够深刻的认识到向量的模为正或者为零,但绝对不为负.如此可为其更加深入的学习向量知识做好铺垫.另一方面,向量有很多的运算规律,一些学生常将其与实数的运算律混淆在一起,在解题中张冠李戴.教学中为使学生更好的掌握向量运算律,应引导学生将向量运算律和实数运算律进行正确的类比.如实数中存在交换律、分配律,通过类比可得到向量的交换律、分配律,以下结论是成立的:①a+b=b+a;②a·(b+c)=a·b+a·c;一些学生通过类比实数的乘法结合律,得出向量的乘法结合律为:(a·b)c=a(b·c),经验证这一类比结论是错误的.由此启发学生在类比的过程中还应进行验证.另外,在进行空间向量知识教学中,可引导学生将其与平面向量进行类比,更加深刻的理解空间向量的计算过程以及计算结论.如已知平面向量a=(x1,y1),b=(x2,y2),则其坐标运算为a+b=(x1+x2,y1+y2),通过类比可得出空间向量的坐标运算为a=(x1,y1,z1),b=(x2,y2,z2)则a+b=(x1+x2,y1+y2,z1+z2).
四、类比法用于圆锥曲线教学
圆锥曲线是高中数学的重点难点,相关习题计算量较大.教学中为提高学生的解题效率,使学生在解题中少走弯路,应注重运用类比法开展教学活动.教学中既要注重引导学生新旧知识的类比,又要注重圆锥曲线之间的类比.通过类比得出相关结论,直接用于解题中.
其一,教学中以椭圆为例,为学生认真讲解椭圆的定义、焦半径、焦点三角形等内容,使学生结合椭圆图形能够牢固的掌握.在此基础上要求学生通过类比尝试着推导双曲线、焦半径、焦点三角形面积的表达式.如图3所示,M为椭圆上一点,椭圆的焦点分别为F1、F2,则三角形F1MF2的面积S=b2tanθ2(∠F1MF2=θ).
通过类比可得出在如图4的双曲线中,F1、F2为焦点,则三角形F1MF2的面积S=b2cotθ2(∠F1MF2=θ).其二,求解圆锥曲线的切线方程在一些测试中时有出现.一些学生不知如何求解,事实上可引导学生联系所学的圆的切线方程,经过类比得出相关结论,更好的用于解题中.其三,教学中要求学生在平时的训练中处处留心,提高类比法应用意识,尤其针对一些证明类的题目,可采用类比法将其结论推广到其他圆锥曲线图形中,掌握相关的解题技巧.
类比法是学习以及研究新问题的重要方法之一.通过类比可使学生在学习中少走弯路,更好的掌握数学知识本质,在解题中以不变应万变.高中数学教学中既要为学生讲解类比,发现相关理论,又要围绕教学内容积极创设相关的问题情景,启发与引导学生进行类比推理,尤其鼓励学生应用类比法注重相互交流经验,不断学习他人长处,不断的充实与提升自己.
参考文献:
[1]涂朦,高中数学教学实践中类比法的应用探讨[J].中学课程辅导,2019(13):145.
[2]董淑芝,类比推理在高中数学教学中的作用及应用方法分析[J].数学学习与研究,2019(16):33.
[责任编辑:李 璟]

