指向学科核心素养的小学数学命题表征

摘 要：在小学数学教育领域中，命题应遵循促进学生核心素养发展的准则，有效结合现实生活，切实培养学生的数学抽象思维、逻辑推理能力、数学建模能力、直观想象能力、数学运算能力、数据分析能力六大核心素养，从而使学生形成良好的必备数学品格及关键数学能力。本文在研究指向学科核心素养的小学数学命题要点基础上，提出了指向学科核心素养的小学数学命题表征，希望能够为广大小学数学教育同人提供有益的命题借鉴。

关键词：小学数学;核心素养;命题

中图分类号：G427                                  文献标识码：A                                       文章编号：2095-9192（2021）11-0006-02

引  言

小学数学命题是对学生学习质量考查的重要教学工作。而小学数学命题工作要明确指向学生的学科素养发展。在小学数学学科的具体命题中，教师应以六大学科素养为导向，设计计算题、解决问题、数据分析、几何推理等多种类型的命题，引导学生在注重实践的基础上，有效提升数学解题能力，培养良好的学科素养。以下结合具体小学数学命题情况进行详细介绍。

一、指向学科核心素养的小学数学命题要点研究

指向学科核心素养的小学数学命题，首先，要贴近现实生活，引导学生在生活化问题情境中利用数学思维正确解答问题。其次，在具体的命题过程中，教师应综合性地设计传统的题目类型，一道题目应考查学生的多项能力，从而促进学生的数学能力均衡发展[1]。最后，小学数学命题还要有效渗透德育教育理念，让学生通过解题获得更为全面的发展。从总体上来说，小学数学命题应建立在应用基础上，反映出学生的真实数学能力，并为学生的数学学习能力发展指明方向。

二、利用简化计算命题，考查数感及运算能力

数学运算素养作为数学学科的基础，对学生的数学学习具有关键性、工具性作用。为了更好地发展和考查学生的数感及运算能力，教师在计算题的命题过程中，可以利用简化计算的题目设计，准确培养学生的简算能力，以取得良好的命题考查效果。

例题1：7.825+3.65+1.175+2.35=（？）这道小数加法的题目，需要学生基于简化计算思想，利用加法交换律，将7.825+3.65+1.175+2.35转化为（7.825+1.175）+（3.65+2.35），从而得出（7.825+1.175）+（3.65+2.35）=9+6+15的答案。学生通过这样的加法交换过程，能够有效地将需要笔算的小数加法，利用口算直接运算出来，从而有效发展学生的运算能力。

三、通过解决问题命题，考查建模及运用意识

解决问题旧称“应用题”，是在现实生产、生活问题的情境下，引导学生利用数学法则解决现实问题的重要数学题目类型。在学科素养指向下，学生解决问题的过程首先应利用“数学抽象”的方法，将题目中的数目、数量转化为抽象的数，之后再利用“数学建模”的途径，找准抽象数之间的内在联系，从而找到解决问题的方法。在解决问题的过程中，教师应注重引导学生结合数学知识在实际生产、生活的实际应用，有效建立数学模型，从而有效发展学生的学科素养。

例题2：某超市购进了20箱牛奶，在加价20%的基础上进行销售，两周后销售出16箱。由于此批牛奶临近保质期，该超市在现销售价的基础上，打5折将剩余的4箱牛奶进行处理，并全部处理出去。已知该超市在此批牛奶的销售过程中，共赢利64元，求每箱牛奶的进价。在解答过程中，学生首先要将每箱牛奶的进价设为x，之后利用数学建模过程，根据“利润=销售额-进价”的思路，列出方程式64=（120%x×16+120%x×50%×4）-20x。其中120%x×16+120%x×50%×4为销售额，20x为进价。之后，学生通过解方程，得出x=40（元）。

四、运用数据分析命题，考查统计及分析观念

数据分析素养是数学学科中统计学部分的关键素养。而数据分析题目往往是小学数学教学中的难点，学生对复杂的数据往往较为抵触。教师可以基于对学生统计及分析能力的考查，为学生设计具有开放性特点的数据分析题目，以培养学生的数据分析素养。

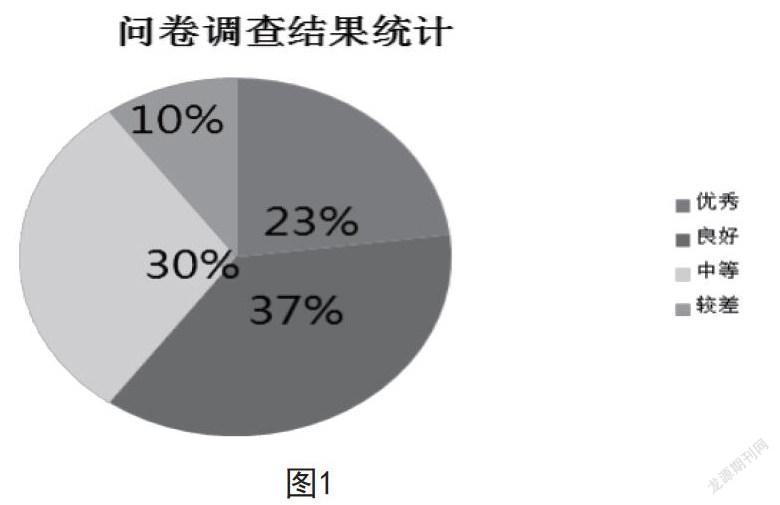
例题3：某校从2000名学生中抽取了200名学生进行‘防疫知识’安全问卷调查，之后将调查结果按“优秀”“良好”“中等”“较差”的标准进行汇总，制作出如下扇形统计图（见图1）。请计算本次问卷调查活动“优秀”及“良好”学生的总数。观察统计结果，你有什么感想？

这道例题主要考查学生对数据的分析能力，以及学生对统计图的读图能力。学生计算本次问卷调查中“优秀”及“良好”学生总数时，可以将“优秀率”与“良好率”相加，再乘以参与调查学生的总人数得出结果，即（23%+37%）×200=120（人）;也可以将“优秀率”与“良好率”分别乘以总人数再相加得出结果，即23%×200+37%×200=120（人），最后根据统计结果发表感想。

五、基于几何推理命题，考查推理及空间观念

几何直观是重要的学科素养。在几何命题过程中，教师可基于对学生的推理能力及空间观念的考查，为学生设计新颖的几何题目，使学生获得逻辑思维的有效提升。

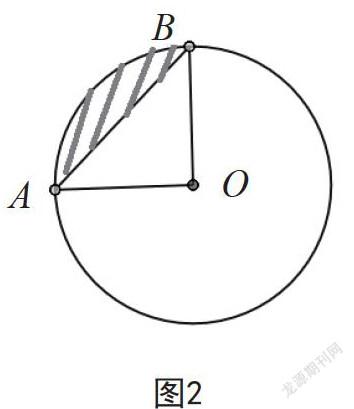
例题4：如图2所示，圆O的面积为4π，三角形AOB为直角三角形，求阴影部分的面积。

這道题目的考查点一是学生对圆面积、扇形面积及三角形面积计算，二是学生对圆周角知识的掌握。在解答本题的过程中，学生首先应明确阴影部分面积为扇形AOB面积-三角形AOB面积;因为三角形AOB为直角三角形，角AOB为直角，因此，扇形AOB面积为4π÷4=π;同时计算出圆半径为2，则三角形AOB的面积为2×2×=2;最后得出阴影部分的面积为π-2。

结  语

总而言之，在小学数学命题过程中，教师应以学科核心素养为指向，通过对试题的巧妙设计，引导学生在真实问题情境中有效发展解题能力，从而获得良好的教学成效。小学生的学科素养发展，不仅对他们当前及今后的数学学习具有关键性作用，还会对他们终身的数学应用能力发展大有裨益。教师通过应用这样的小学数学命题模式，可以促使学生将所学知识与具体的实践、应用进行有效联系，从而培养学生必备的数学品格和关键的数学实践能力。

[参考文献]

龚祖华.基于核心素养的小学数学命题设计要点[J].辽宁教育，2020（13）：75.

基金项目：本文系福建省教育科学“十三五”规划2020年度课题“指向学科核心素养的小学数学纸笔测试命题改进研究”（课题批准号：FJJKXB20-1087）的研究成果。

作者简介：林雪芬（1978.10-），女，福建莆田人，高级教师。