定目标·悟原理·寻路径

王学先 杨兴建 吴禹杰

摘  要：中考对尺规作图的考查涉及多种形式，不再是单一的对作图技法操作进行考查，而是把作图与计算、证明、分析、判断等数学思维活动有效融合，既体现了动手实践的数学思维活动，也考查了学生运用数学思考解决问题的能力. 尺规作图在培养学生数学思维品质的同时，能够提高学生的数学学科核心素养. 文章对2020年中考“尺規作图”的几类试题进行分析，从目标、原理、路径三个方面挖掘这类试题的考查方式和命题特色，为初中数学尺规作图问题的教学和命题提供参考.

关键词：尺规作图;作图原理;命题特色;作图路径

2020年中考“尺规作图”部分的试题设计，在全面考查尺规作图的基础上，着重考查了尺规作图的目标、原理和路径，试题新意迭出且深意彰显. 其中，尺规作图目标、原理、路径分别考查基本作图的几何性质、作图依据和作图方法. 文章对2020年中考尺规作图试题进行研究，为更好地把握尺规作图的教学要求和命题思路提供一些探索.

一、尺规作图及试题考查情况分析

1. 尺规作图

尺规作图起源于古希腊的数学问题，指用没有刻度的直尺和圆规作图，并且只使用有限次，来解决不同的平面几何作图题. 观察利用尺规作图所得的几何图形，我们可以将一些结论由特殊引向一般，并归纳出一般性结论. 在中考试题中，尺规作图一般被分为两类：一类是基本作图;另一类是利用两种或两种以上的基本作图进行尺规作图.

2. 课程标准的要求

《义务教育数学课程标准（2011年版）》（以下简称《标准》）对尺规作图作出了以下要求.

（1）能用尺规完成以下基本作图：作一条线段等于已知线段;作一个角等于已知角;作一个角的平分线;作一条线段的垂直平分线;过一点作已知直线的垂线.

（2）会利用基本作图作三角形：已知三边、两边及其夹角、两角及其夹边作三角形;已知底边及底边上的高线作等腰三角形;已知一直角边和斜边作直角三角形.

（3）会利用基本作图完成：过不在同一直线上的三点作圆;作三角形的外接圆、内切圆;作圆的内接正方形和正六边形.

（4）在尺规作图中，了解作图的道理，保留作图的痕迹，不要求写出作法.

3. 试题考查方式分析

综观2020年全国各地区中考试题，在尺规作图这一部分内容的考查中，着重体现了尺规作图和几何推理考查的双向性. 具体包括以下三类题型.

（1）作法应用类试题. 这类试题在给出图形基本作法的情况下，要求学生领悟作图原理，结合相应的图形性质进行几何推理、证明和计算. 该类型试题既注重对学生的几何推理能力的考查，又体现了对数学抽象、逻辑推理、直观想象和数学运算等素养的考查.

（2）作法原理类试题. 这类试题是在给定作法和保留作图痕迹的前提下，要求学生填写相应的作图依据. 该类型试题对学生是否深刻掌握其背后的作图原理要求较高，充分发挥考试导向功能，引导教师在平时教学中重视对尺规作图原理的教学.

（3）作法操作类试题. 这类试题要求学生在有限的条件下领悟作图原理，经过合情推理获得正确的作图方法，并按要求完成作图，且保留作图痕迹. 该类试题注重在学生正确掌握作图原理的前提条件下，考查基本方法和基本活动经验的落实情况.

二、考查目标和命题特色分析

1. 五种基本作图

（1）作一条线段等于已知线段.

例1 （湖南·邵阳卷）如图1，线段AB = 10 cm，用尺规作图法按如下步骤作图.

（1）过点B作AB的垂线，并在垂线上取BC =[12]AB;

（2）连接AC，以点C为圆心，CB为半径画弧，交AC于点E;

（3）以点A为圆心，AE为半径画弧，交AB于点D，即点D为线段AB的黄金分割点.

则线段AD的长度约为      .（结果保留两位小数，参考数据：[2]≈ 1.414，[3]≈ 1.732，[5]≈ 2.236.）

分析：此题考查了基本作图中的“作一条线段等于已知线段”，涉及勾股定理、方程、近似数等基础知识，考查学生应用数学知识解决问题的能力.

此题属于尺规作图“作法应用类”试题，以黄金分割点为背景，以直角三角形为载体进行命制. 虽然出现了“过直线上一点作该直线的垂线”和“作一条线段等于已知线段”两种基本作图，但从已给的作图痕迹来看，重点考查作图后的计算. 此题关注知识之间的联系和交会，较好地促进了学生对尺规作图内容的掌握和运用，提高了学生对知识的应用和转化能力.

简解：由作图过程，可知△ABC为直角三角形，且CE = BC =[12]AB = 5，AD = AE. 根据勾股定理，求出AC =[55]. 再求出AD = AE =[55-5][≈ 6.18]（cm）.

（2）作一个角等于已知角.

例2 （福建卷）如图2，C为线段AB外一点.

（1）求作四边形ABCD，使得CD∥AB，且CD = 2AB.（要求：尺规作图，不写作法，保留作图痕迹.）

（2）在（1）的四边形ABCD中，AC，BD相交于点P，AB，CD的中点分别为M，N，求证：M，P，N三点在同一条直线上.

分析：此题考查了基本作图中的“作一个角等于已知角”和“作一条线段等于已知线段”，涉及平行线和相似三角形的判定与性质等知识，考查学生的推理能力、空间观念、几何直观、化归与转化数学思想.

此题属于尺规作图“作法应用类”试题. 以作四边形ABCD为背景，要求学生熟练掌握作图方法. 解决此题的关键是添加适当的辅助线构造相似三角形，结合相似三角形的判定与性质进行推理和计算，问题的解决应用了转化的数学思想方法，培养了学生的几何直观，提高了学生的逻辑推理能力.

简解：（1）如图3，四边形ABCD即为所求.

（2）如图4，先利用已知条件证明[△ABP∽][△CDP，] 得[ABCD=APCP]. 根据中点的性质，转化得到[AMCN=APCP]. 连接[MP，NP，] 由[∠BAP=∠DCP，] 即可以证明[△APM∽][△CPN]. 所以[∠APM=∠CPN]. 由点[P]在[AC]上，得到[∠APM+∠CPM=180°]. 进一步得到[∠CPN+∠CPM=][180°]，从而证明M，P，N三点在同一条直线上.

（3）作一条线段的垂直平分线.

例3 （广东卷）如图5，在菱形ABCD中，∠A = 30°，取大于[12]AB的长为半径，分别以点A，B为圆心作弧相交于两点，过此两点的直线交AD边于点E（作图痕迹如图所示），连接BE，BD. 则∠EBD的度数为       .

分析：此题考查基本作图中的“作一条线段的垂直平分线”，属于单一模型. 此题涉及菱形、垂直平分线、等腰三角形的性质和三角形的内角和定理，考查学生的逻辑推理、几何直观、读取信息及利用信息解决问题的能力.

此题属于尺规作图“作法应用类”试题，将基本作图问题和菱形有机结合，设计别出心裁. 熟练掌握线段垂直平分线的作法、菱形的性质、三角形内角和定理是解决此题的关键.

简解：根据垂直平分线的性质，得EA = EB. 由四边形ABCD是菱形，得AB = AD. 因为∠A = 30°，所以∠ABE = 30°，∠ABD = 75°. 根据∠EBD = ∠ABD - ∠ABE，求出∠EBD = 45°.

（4）作一个角的平分线.

例4 （湖南·长沙卷）人教版初中数学教科书八年级上册第48页告诉我们一种作已知角的平分线的方法.

已知：[∠AOB].

求作：[∠AOB]的平分线.

作法：（1）以点O为圆心，适当长为半径画弧，交OA于点M，交OB于点N;

（2）分别以点M，N为圆心，大于[12MN]的长为半径画弧，两弧在[∠AOB]的内部相交于点C;

（3）画射线OC，射线OC即为所求（如图6）.

试根据提供的材料完成下面问题.

（1）这种作已知角平分线的方法的依据是     .（填序号）

①[SSS]   ②[SAS]   ③[AAS]   ④[ASA]

（2）试证明OC为[∠AOB]的平分线.

分析：此题考查了尺规作图中的“作一个角的平分线”和全等三角形的判定定理. 此题源于教材，通过考查学生对基本作图依据的探究，培养学生的逻辑推理能力.

此题属于尺规作图“作法原理类”试题，需要学生探索作图依据，完成逻辑推理. 解决问题的关键是掌握基本作图方法及全等三角形的判定和性质.

简解：（1）①.

（2）根据作图过程，可得OM = ON，OC = OC，CM = CN. 由“SSS”可以证得△MOC ≌ △NOC. 从而得到∠AOC = ∠BOC，即OC为[∠AOB]的平分线.

（5）过一点作已知直线的垂线.

① 过直线上一点作已知直线的垂线.

例5 （内蒙古·赤峰卷）小琪同学和爸爸妈妈一起回老家给奶奶过生日，他们为奶奶准备了一个如图7所示的正方形蛋糕，蛋糕的每条边上均匀镶嵌着4颗巧克力. 爸爸要求小琪只切两刀把蛋糕平均分成4份，使每个人分得的蛋糕和巧克力数都相等.

（1）试在图7中画出一种分法.（无需尺规作图）

（2）如图8，小琪同学过正方形的中心切了一刀，试用尺规作图帮她作出第2刀所在的直线.（不写作法，保留作图痕迹.）

[图7][图8]

分析：此题考查作图的应用与设计，涉及正方形的性质和中心对称图形性质的综合应用，考查学生的几何直观、逻辑推理和知识迁移能力.

此题属于尺规作图“作法操作类”试题. 以切蛋糕的实例为背景命题，贴近学生生活实际，能引发学生积极思考，体现了数学“既来源于生活，又服务于生活”的特点. 第（2）小题用到了线段垂直平分线的性质，属于用不同的知识解决相同的问题，凸显了知识之间的联系.

简解：（1）如图9，根据正方形的对角线互相垂直平分，得直线a、b即为所求.

（2）如图10，连接AC交直线EF于点O，过点O作HG⊥EF，直线HG即为已知线段的垂直平分线，借助垂直平分线的性质解决问题.

② 过直线外一点作已知直线的垂线.

例6 （内蒙古·鄂尔多斯卷）在四边形ABCD中，AD∥BC，∠D = 90°，AD = 8，BC = 6，分别以点A，C为圆心，大于[12]AC的长为半径作弧，两弧交于点E，作射线BE交AD于点F，交AC于点O，若点O是AC的中点，则CD的长为（   ）.

分析：此题考查了基本作图中的“过直线外一点作已知直线的垂线”，涉及勾股定理、线段垂直平分线和全等三角形的判定与性质的综合运用，考查学生的推理能力和计算能力.

此题属于尺规作图“作法應用类”试题. 根据“线段垂直平分线上任意一点，到线段两端点的距离相等”，确定“EO垂直平分线段AC”是解决问题的关键.

简解：如图12，连接FC. 根据基本作图，可以得到OE⊥AC. 因为点O是AC的中点，所以OE垂直平分线段AC. 由线段垂直平分线的性质，得AF = FC. 根据“ASA”证明△FOA ≌ △BOC，因此AF = BC = 6. 等量代换得到FC = AF = 6. 利用线段的和差关系求出FD = AD - AF = 2. 在Rt△FDC中，利用勾股定理求出CD =[42]. 故此题选择选项A.

2. 两种基本作图模型综合考查

（1）作一条线段等于已知线段和作一个角的平分线.

例7 （江苏·泰州卷）如图13，已知线段a，点A在平面直角坐标系xOy内.

（1）用直尺和圆规在第一象限内作出点P，使点P到两坐标轴的距离相等，且与点A的距离等于a.（保留作图痕迹，不写作法.）

（2）在（1）的条件下，若a =[25]，点A的坐标为[A3，1]，求点P的坐标.

分析：此题考查了基本作图中的“作一条线段等于已知线段”和“作一个角的平分线”. 此题涉及坐标与图形的性质、角平分线的性质、勾股定理等知识，考查了数形结合思想、方程思想，以及逻辑推理和数学运算能力.

此题属于尺规作图“作法应用类”试题. 此题以平面直角坐标系为载体，通过尺规作图作第一象限的角平分线，通过构造直角三角形，利用勾股定理，借助方程思想解决问题. 解题的关键是掌握角平分线的作法及两点之间的距离公式，明确如何正确作图.

简解：（1）如图14，先作第一象限的角平分线OM，再以点A为圆心、a为半径画弧，交OM于点P，则点P为所求.

分析：此题考查了基本作图中的“作一条线段的垂线”和“作一个角的平分线”，其中全等三角形的判定和性质、角平分线的性质是作图的依据，考查学生的推理能力.

此题属于尺规作图“作法应用类”试题. 以直角三角形为背景，要求学生熟练掌握作图方法和技巧，能根据作图步骤正确辨别所作图形，并熟练应用其性质解决问题.

简解：根据题目条件容易证明△ADE ≌ △ADB，可判断选项A，B正确. 再根据“同角的补角相等”，可以判断∠EDC = ∠BAC. 故此题选择选项D.

（3）作直角三角形的外接圆和作一个角的平分线.

例9 （青海卷）如图17，在Rt△ABC中，∠C = 90°.

（1）尺规作图：作Rt△ABC的外接圆⊙O;作∠ACB的平分线交⊙O于点D，连接AD.（不写作法，保留作图痕迹.）

（2）若AC = 6，BC = 8，求AD的长.

分析：此题考查了基本作图中的“作一条线段的垂直平分线”和“作一个角的平分线”，借助线段垂直平分线的性质准确找到直角三角形外接圆的圆心是解决问题的关键. 此题既考查了学生对基本作图的掌握情况，又考查了学生寻找知识之间逻辑关系的能力.

此题属于尺规作图“作法应用类”试题，涉及三角形的外接圆、角平分线、垂直平分线的性质及圆周角与圆心角的关系，考查学生的基本作图技能和基本活动经验.

简解：（1）如图18，作Rt△ABC斜边AB的垂直平分线，根据“直角三角形斜边上的中线等于斜边的一半”，即可作Rt△ABC的外接圆⊙O. 再作∠ACB的角平分线CD，交⊙O于点D，连接AD即可.

分析：此题综合考查了“作一条线段的垂直平分线”和“作一个角的平分线”. 作图依据是角平分线和线段垂直平分线的性质，考查了学生的几何直观和逻辑推理能力.

此题属于尺规作图“作法操作类”试题，是三角形、圆、作角的平分线和线段的垂直平分线的综合题型. 正确掌握角平分线和线段垂直平分线的作法是解题的关键.

简解：如图21，作出∠A的平分线和线段BC的垂直平分线，找到它们的交点，即为圆心O，再以OB为半径画出⊙O即可.

3. 开放性作图题

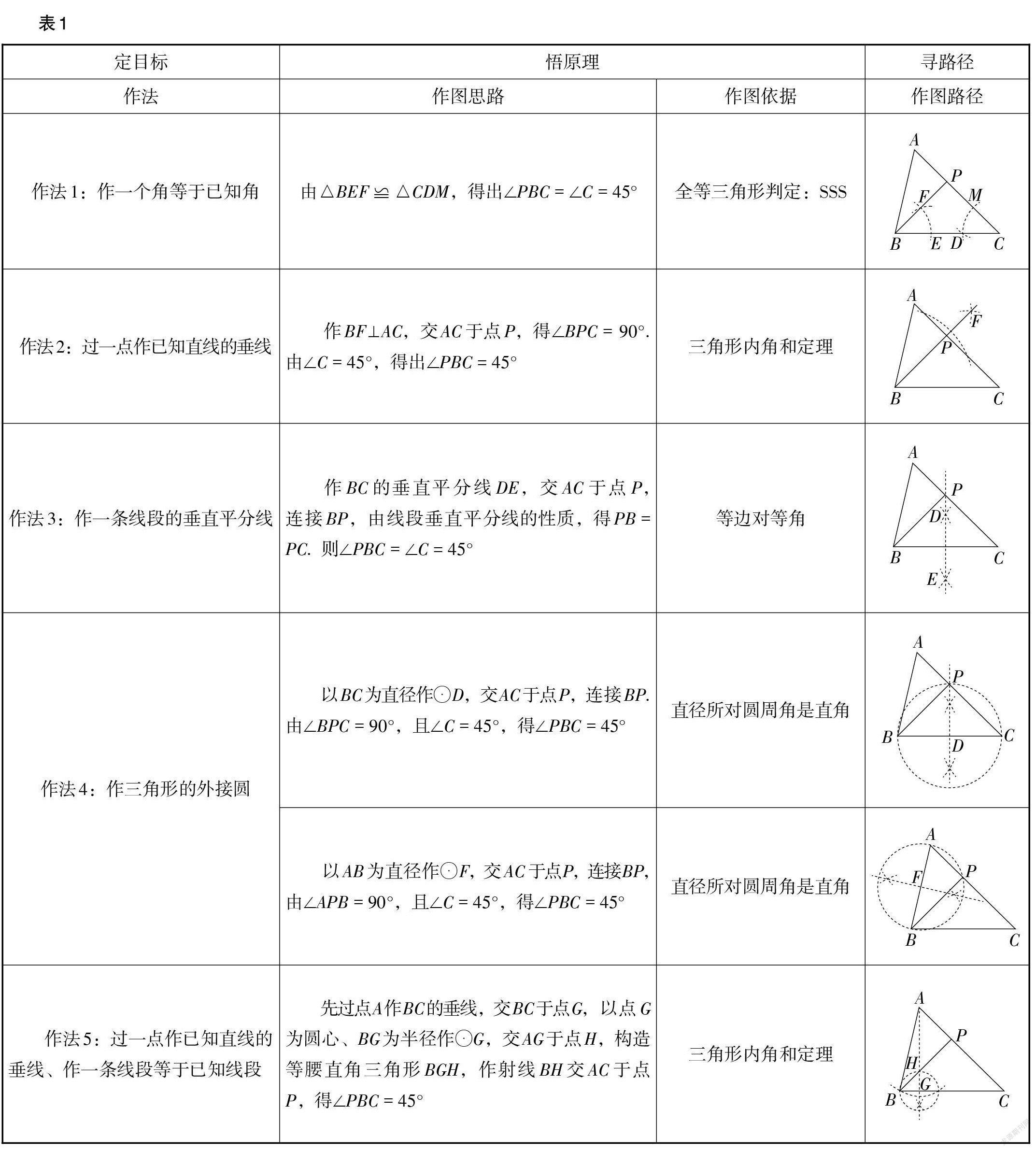
例11 （陕西卷）如图22，已知△ABC，AC > AB，∠C = 45°. 试用尺规作图法，在边AC上求作一点P，使∠PBC = 45°.（保留作图痕迹，不写作法.）

分析：此题考查了基本作图中“作一个角等于已知角”“过一点作已知直线的垂线”“作一条线段的垂直平分线”“作三角形的外接圆”“作一条线段等于已知线段”. 此题强调作图的方法和作图原理，形式新颖，彰显创新能力，要求学生进行多方位、多角度、多层次地探究，基于判断寻找解决问题的路径，对于开阔学生的思维、培养学生的创新能力具有重要意义.

此题属于尺规作图“作法操作类”试题，需要学生动手操作完成，既能丰富学生的基本活动经验，又能激发学生的学习兴趣和对知识的探究欲. 根据尺规作图法，在边AC上求作一点P，使∠PBC = ∠C = 45°. 解决尺规作图问题的关键在于掌握基本作图的方法、明确基本作图的原理、理解基本作图的依据，以及寻找基本作图的路径. 此题属于解题方法多样的开放性试题，这样的试题能避免学生死记解题方法，需要学生从不同的角度思考问题，寻求多样性的解题方法.

作图方法和依据如表1所示.

三、教学建议

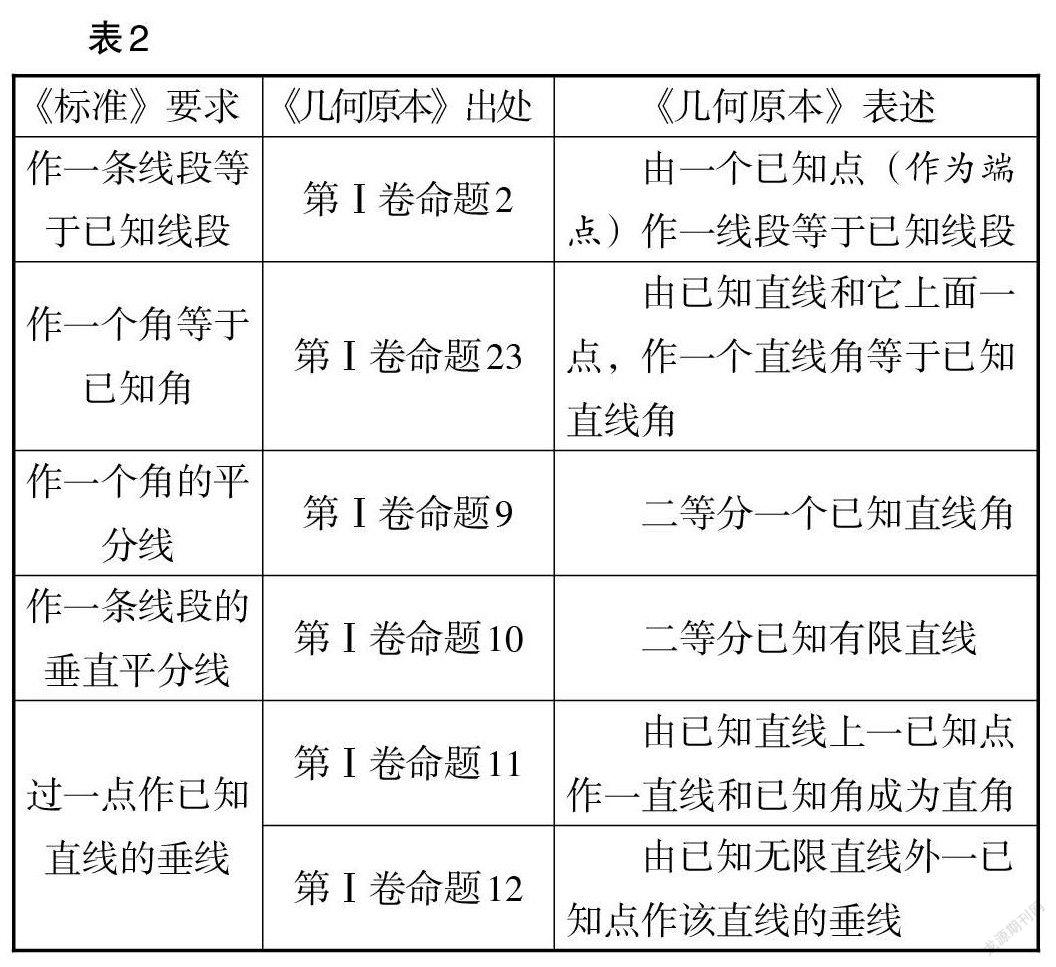
1. 研读尺规作图文化，深挖几何知识背景

尺规作图作为几何作图最基本的形式，是演绎推理的一种体现.《几何原本》中也给出了多种尺规作图的方法.《标准》对尺规作图的要求在《几何原本》中都有所体现. 不难发现，尺规作图这种演绎推理的形式，为我们提供了作图的依据和原理，这在几何证明中是不可或缺的. 表2是《标准》中要求的五类基本作图，在《几何原本》一书中找到了出处.

[《标准》要求 《几何原本》出处 《几何原本》表述 作一条线段等于已知线段 第Ⅰ卷命题2     由一个已知点（作为端点）作一线段等于已知线段 作一個角等于已知角 第Ⅰ卷命题23     由已知直线和它上面一点，作一个直线角等于已知直线角 作一个角的平分线 第Ⅰ卷命题9     二等分一个已知直线角 作一条线段的垂直平分线 第Ⅰ卷命题10     二等分已知有限直线 过一点作已知直线的垂线 第Ⅰ卷命题11     由已知直线上一已知点作一直线和已知角成为直角 第Ⅰ卷命题12     由已知无限直线外一已知点作该直线的垂线 ][    表2]

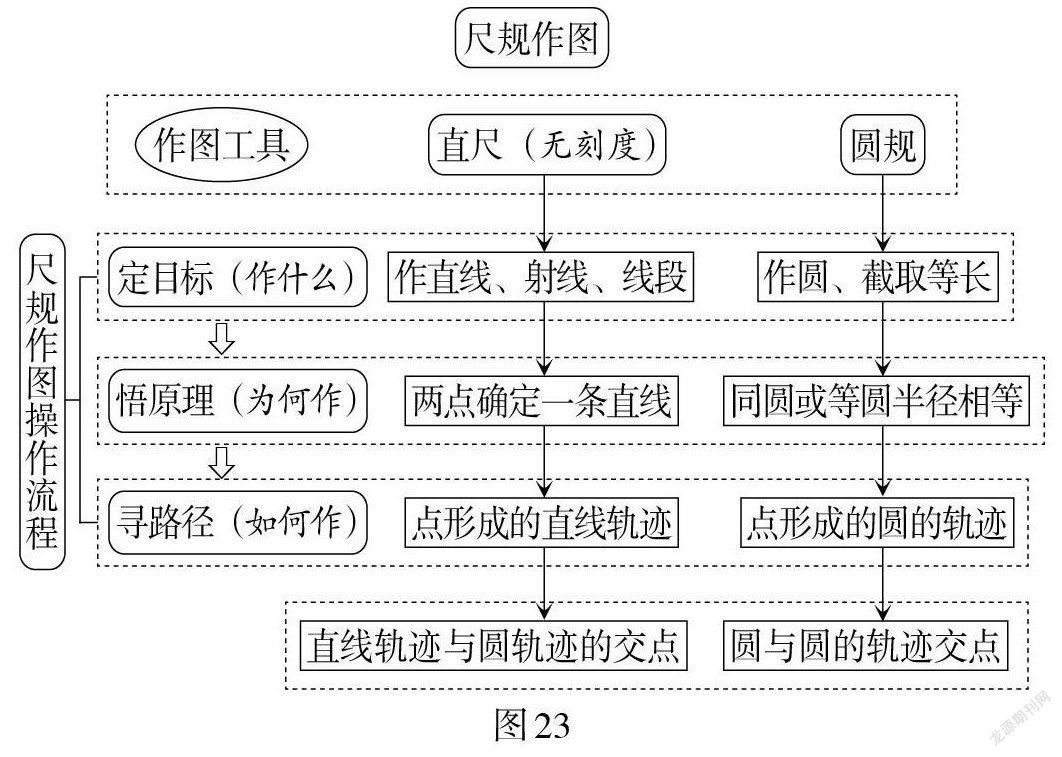
数学教育家G.波利亚在《数学的发现：对解题的理解、研究和讲授》一书中曾提到，在中学课程里传统的作图法几乎全部是双轨迹模型的直接应用. 基于此，通过对数学文化的研究，领悟数学几何语言的本质和作图原理，形成如图23所示的解题结构.

2. 深究尺规作图原理，促进数学素养提升

在平时的几何教学中，教师要注重合情推理与演绎推理的相互配合，数学思想的相互渗透，科学合理的将理论与操作相结合，提升学生的数学思维能力，促进对学生数学学科核心素养的培养. 尺规作图教学是训练学生逻辑推理能力的重要内容之一，教学中应抓住知识的本质，注重知识的生成过程，强化知识的应用，在应用正向思维的同時，也要强调逆向思维，并规范学生作图语言的表达，引导学生深刻体会作图原理，准确提取作图依据，对已有知识进行系统化的迁移、内化和应用，做到一题多解，并且将多解归一.

3. 规范几何语言表达，理清尺规作图路径

数学语言是数学思维的显性体现，它往往会通过符号、字母、文字传达一些重要的信息. 在教学时，教师不但要引导学生熟悉尺规作图规范，而且要重视学生在尺规作图知识内化过程中的数学语言表达，要求学生会描述尺规作图相应的作图步骤.

四、命题建议

中考试卷中的尺规作图试题能很好地发挥尺规作图的教育价值，指导日常教学的方向，即抓住尺规作图的本质，促进数学素养的建构. 尺规作图试题的命制常常要利用图形创设一种情境，即在某种情境条件下，强调观察、操作、推理，由学生自己动手解决问题. 要求学生能规范作出符合要求的图形，并明晰其中的原理，是一种具有挑战的创造性活动，能够激发学生的兴趣和创造性. 尺规作图问题能够考查学生思维的开放性和创新性，题型呈现上可以是选择题、填空题或解答题，考查方式包括尺规作图与作法操作、尺规作图与几何计算、尺规作图与证明猜想、尺规作图与方案设计、尺规作图与图案设计、尺规作图与实际应用等.

参考文献：

[1]中华人民共和国教育部制定. 义务教育数学课程标准（2011年版）[M]. 北京：北京师范大学出版社，2012.

[2]欧几里得. 几何原本[M]. 兰纪正，朱恩宽，译. 西安：陕西科学技术出版社，2003.

[3]波利亚. 数学的发现：对解题的理解、研究和讲授[M]. 刘景麟，曹之江，邹清莲，译. 北京：科学出版社，2006.

[4]陈锋，钟鸣. 一道中考尺规作图题的解法分析及教学启示[J]. 中国数学教育（初中版），2019（9）：44-46.

[5]肖世兵. 近三年中考“尺规作图”命题分析、感悟及实践[J]. 中学数学杂志，2020（6）：60-62.