非参数估计法环状静电传感器灵敏度仿真研究*
钱宇加,阚 哲,刘 晓,罗 琳
(辽宁石油化工大学 信息与控制工程学院,辽宁 抚顺 113001)
0 引 言
在气力输送过程中,广泛存在有气固两相流状态,固相颗粒与管路、颗粒之间的摩擦、碰撞、分离,使颗粒带上了静电。早在20世纪60,70年代,国外就有研究者注意到静电现象并对它展开了深入研究。许多学者对静电传感器模型结构等进行了大量的探讨。张帅等人研究了阵列式条形电极且绝缘管道为方形的静电传感器模型,通过实验装置得到的实际结果与仿真基本一致[1]。通过COMSOL软件设计了具有网状电极的静电传感器,使得灵敏度的分布更均匀[2]。李健等人对传感器模型结构进行改进设计了矩阵式电极静电传感器,为静电传感器模型优化提供了一个方向[3]。静电传感器[4]具有结构模型简单,价格比较低,设备安装简单方便,并且适用于一些环境恶劣的场所等多方面的优点[5,6]。
目前对于静电传感器电极的安装方式主要可以分为侵入式与感应式[7],其中侵入式颗粒的流动容易造成电极的磨损,而感应式对颗粒流动不造成影响,主要包括圆环式静电传感器[8]、立体网状静电传感器[9]、插入式棒状静电传感器和阵列式静电传感器[10]。灵敏度是评价静电传感器工作特性的重要参数。
本文针对圆环式静点传感器的灵敏度问题,基于Maxwell有限元仿真软件进行二维、三维的建模分析,并且通过非参数估计法得到静电传感器的灵敏度公式,经过实验验证,采集到的实际电压与仿真得到的电荷量间的对应关系基本一致。
1 静电传感器原理
1.1 传感器结构
静电传感器示意图如图1所示。图中,环状静电传感器由PVC管、金属屏蔽罩和铜电极环组成。

图1 静电传感器
1.2 静电传感器原理
静电传感器检测的是运动的固体颗粒所带的自然电荷。固体颗粒之间的碰撞以及颗粒与管壁摩擦会产生静电荷,使管壁外的电极产生静电感应现象。图2为静电传感器等效电路。
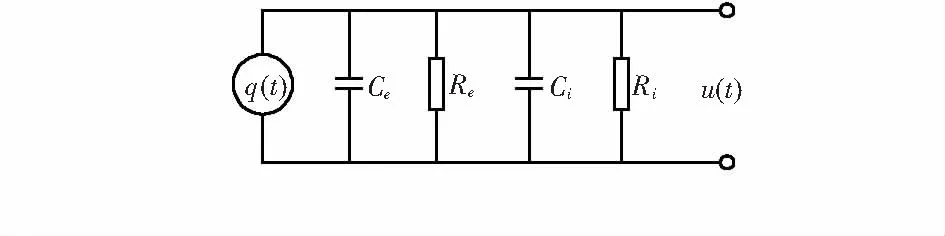
图2 静电传感器等效电路
图2中,感应电荷为q(t),输出电压u(t),Re,Ce为电极等效电阻与等效电容,Ri,Ci为前级放大器的等效输入电阻与输入电容。根据基尔霍夫电流定律和拉普拉斯变换可以得到
(1)
其中,R=ReRi/(Re+Ri),C=Ce+Ci,当|RCs|≪1时,感应电荷的测量模型为
u(t)≈R·q(t)
(2)
从表达式(2)可以得到静电传感器输出电压值与电极上感应的电荷量呈线性关系,因此,在设计检测电路时,可以使用电荷检测电路。
1.3 测量转换电路
图1中静电传感器电极引线输出信号需要经预处理,然后进行滤波放大供采集器采集。转换电路形式如图3所示。

图3 转换处理电路
在图3中,预放大电路1选用AD549,将这一级作为静电岛模块,可以使电极引线加长至3 m左右。跟随器2采用OPA129。放大器3~5均选用OP37,放大器3与两个电阻和两个电容构成低通滤波器,放大器4为电压放大电路,放大器5为跟随隔离电路。采集器选用NI采集卡,上位机接收软件采用LabVIEW软件制作。实验室测量系统如图4所示。

图4 传感器实验系统
2 静电传感器理论模型
2.1 理论模型
(3)
式中φ(r,θ,z)为电势分布函数,ρ(r,θ,z)为空间中的体电荷密度,ε(r,θ,z)为电介质的介电常数,Γs,Γd分别为屏蔽罩和电极所对应的空间位置,Cons为一个常数。
在静电传感器的理论模型中,静电场的静电位函数满足标量泊松方程,若空间中没有自由电荷分布,则ρ=0,电位函数φ(r,θ,z)满足拉普拉斯方程

(4)
通过求解电位函数的拉普拉斯方程的通解以及泊松方程的特解,两者相结合可以得到静电位函数的泊松方程的通解,然后根据满足的边界条件即可求得泊松方程通解中的未知常数,得到电位函数φ(r,θ,z)关于各个自变量的关系表达式。
2.2 模型建立
1)静电传感器模型的建立
在Maxwell软件建立三维静电传感器模型如图5所示。
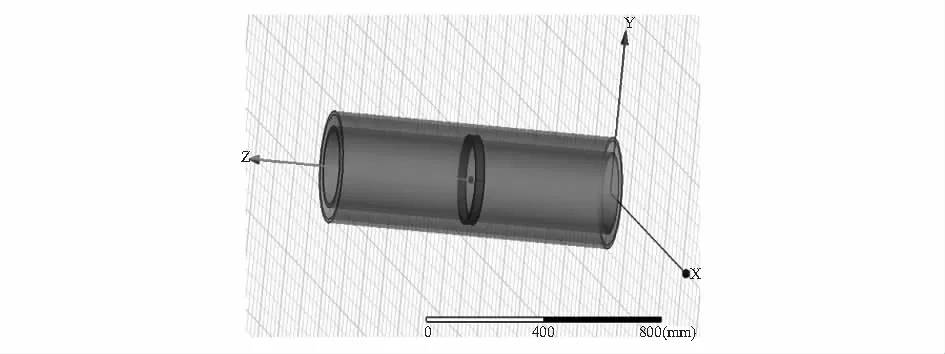
图5 静电传感器实体模型
2)网格的剖分
在静态场中Maxwell软件具有网格自动加密能力,因此,一般情况下无须进行手动剖分就能得到满足工程要求的网格。利用Maxwell软件绘制出2 D不同空间位置的电场强度矢量图以及云图,其中径向空间中心位置的电场矢量图以及云图采用默认的XY笛卡尔坐标系。轴向中心位置的电场矢量图以及云图采用绕着Z轴的极坐标形式。在Maxwell 3D后处理过程中,需要使用场计算器得到电极的感应电荷量,并根据以下方程即可得到静电传感器空间灵敏度
(5)
式中q(r,ε,θ,z)为感应电荷量,Q为带电颗粒自身所带的电荷量。
3 非参数估计数学模型
3.1 非参数估计
非参数估计是已知样本所属类别,但未知总体概率密度函数的形式,要求直接推断概率密度函数本身。
3.2 非参数方法
用于函数估计的非参数方法大致有三种:核方法、局部多项式方法、样条方法。核方法适用于中小规模的数据集,假设x1,x2,…,xn为随机变量为x的样本,x的概率密度函数为f(x),给定一个核函数K(x)和一个称为“窗宽”的正数h,在n→∞,h→0时,核密度估计可表示为
(6)
式中n为样本数量,h为带宽,也称为窗口,K(x)为核函数,它通常满足以下条件
(7)
当n→∞,h→0,nh→∞时,(x)依概率收敛于f(x)。
当h取值越大,则核密度估计函数(x)曲线越平滑,估计的偏差相对较大;反之,(x)与样本能够拟合的较好,但曲线可能很不光滑。根据Maxwell所计算得到的样本点(Z1,Q1),(Z2,Q2),…,(Z19,Q19),选择合适的核函数以及窗宽h可以估计得到样本曲线的函数表达式为
(8)

运用R语言编程和非参数核估计方法,选择合适的核函数K(x)以及窗宽h,并且通过引入拟合优度来判断出拟合的优劣。拟合优度的定义为
R2=1-RSS/TSS
(9)
其中,RSS为残差平方和,TSS为总离差平方和,也可以表示为
(10)
计算得到拟合优度R2=0.950 6,说明拟合曲线对样本点的拟合较好,为灵敏度公式选取高斯分布提供了一定的理论依据。基于非参数估计理论,确定静电传感器感应电荷量公式
(11)
式中Q(r,ε,z)为在绝缘管道相对介电常数为ε并且带电颗粒在径向位置r,轴向位置z时电极上感应到的电荷量,A(r,ε)和B(r,ε)是r和ε的函数,A(r,ε)决定Q(r,ε,z)的幅值,B(r,ε)决定Q(r,ε,z)的形状。最终,确定静电传感器灵敏度公式
(12)
4 仿真与实验
根据有限元仿真发现,带电颗粒在PVC管道中的空间位置,传感器电极的尺寸等都与静电传感器的空间灵敏度特性有关。
4.1 仿真实验
4.1.1 电极宽度对轴向径向空间灵敏度特性
将静电传感器电极宽度W分别设为30,40,50,60 mm,管道直径D为100 mm,并利用场计算器计算得到相应的静电传感器的灵敏度,如图6所示。
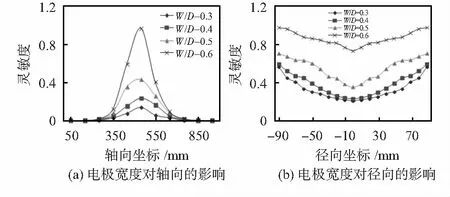
图6 不同电极宽度对轴向径向灵敏度的影响
从图6中可以看出在一定范围内,W/D越大,静电传感器的灵敏度相对越高,灵敏度的增幅则在减小,在径向中心位置的两侧可以看出W/D为0.4时比较稳定,因此,W/D为0.4相对是最合适,即本文管道直径为100 mm时采用宽度为40 mm的电极。
4.1.2 绝缘管相对介电常数对轴向径向空间灵敏度特性
将绝缘管的相对介电常数分别设为3,6,9,12,并利用场计算器计算得到相应的静电传感器的灵敏度,如图7所示。
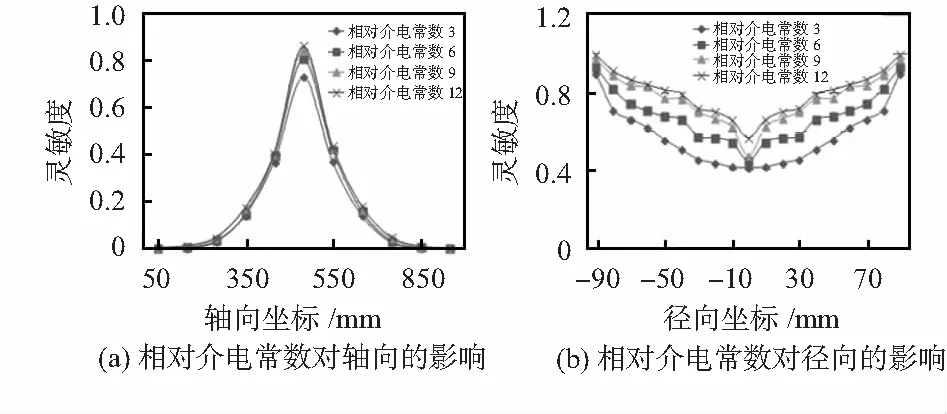
图7 不同相对介电常数对轴向径向灵敏度的影响
从图7可以看出,在一定范围内,绝缘管相对介电常数越大,则静电传感器灵敏度越高,在径向中心位置的两侧,相对介电常数为3的绝缘管的变化比较稳定,因此,本文采用相对介电常数接近3的PVC作为绝缘管的材料。
4.1.3 带电颗粒在不同空间位置的灵敏度特性
在W/R为定值时,带电粒子在不同空间位置处的灵敏度,如图8所示。

图8 单个颗粒在不同空间位置处的仿真结果
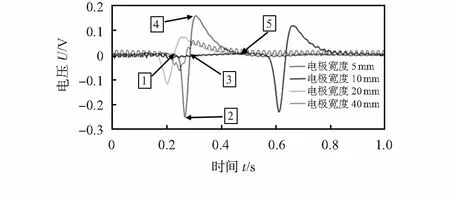
从图8可以得到一个结论:颗粒在轴向位置450 实验设备主要包括静电传感器模块、信号处理模块、信号采集以及信号显示模块等。传感器有4根信号输出线,自下往上分别代表感应电极宽度为5,10,20,40 mm,让塑料小球从同一高度自由落体,通过采集实际数据绘制图形如图9所示。 图9 单个颗粒在不同电极宽度下的电压值 因为感应电荷量与电流的关系满足以下条件 (13) 由上式可知,在Q-t图形中曲线的斜率即为电流,并且由下式 U=IR (14) 可知,电压波形与电流波形形状相似,只有幅值的差异。从图9中还可以发现,电极宽度越宽,测得的电压信号的幅值越小。管道内空间灵敏度越均匀,那么电压信号大小变化越缓慢,则其幅值就越小,这与仿真的结果一致。 本文采用改进静电传感器输出信号处理电路使得信号输出线可以加长到2~3 m。引入非参数核估计方法,采用高斯核函数拟合出感应电荷量的形式,这为灵敏度公式采用高斯分布提供了一定的理论依据。对静电传感器进行理论分析,得到了传感器参数对空间灵敏度特性的影响,确定在管道直径为100 mm时采用宽度为40 mm的电极。并且电极的材料经仿真结果对比,最终采用相对介电常数接近3的PVC作为绝缘管的材料。最后简单介绍了实验设备和实验的结果分析,实验结果与Maxwell仿真的结果匹配,表明建立的实验模型有效。4.2 实 验
5 结 论

