城市轨道交通列车引起的环境振动传播衰减规律研究

潘晓岩

（中国铁路设计集团有限公司 机械动力与环境工程设计研究院，天津300308）

1 前言

随着城市的发展，轨道交通引起的环境振动问题也日益突出。为了掌握城市轨道交通沿线振动情况、减缓沿线振动影响，有必要进行城市轨道交通列车通过时的振动传播衰减规律研究[1]。

对于振动传播规律的研究，主要有解析法、数值计算法及现场实测法。闫维明等[2]通过对某地铁运营引起的环境振动进行了实测与分析，在研究中给出了不同距离处振动的频谱特性及各频带下振动随距离的衰减，并根据实测结果进行了回归分析，提出计算振动随距离衰减的经验公式；郑金贤[3]在军都山隧道进行了列车通过隧道时的振动测试，得到了不同距离处的振动测试结果；张祎[4]对广州地铁1号线3处工点进行了地铁隧道段的地面测试及振动传播衰减研究，证实了地铁振动强度不是随距离单调衰减而是存在一个放大区域；单涛涛等[5]对上海某线区间的地面振动进行了监测，并结合二维有限元数值计算，也得到了同样结论。

以上研究对不同运行条件的地铁列车地下线、地面振动影响进行了测试，但未同时对隧道内列车振动源强进行测试，难以得到列车准确的运营条件，而且上述研究中通过振动测试结果得到的振动预测公式与《环境影响评价技术导则城市轨道交通》(HJ 453—2018)[6]回归分析方法不同。基于此，本文对某地铁线路隧道及地面同步进行了振动测试，研究了各传播路径的振动传播损失，并根据测试数据进行了回归分析方法研究，得出了用于该地铁所属市域内的振动传播衰减预测公式，以期为城市轨道交通沿线振动预测及减振设计提供参考。

2 振动测试及测点

为了解城市轨道交通列车运营时振动在各传播途径上的传递损失特点、分析振动在地面传播衰减的影响因素，在地面及隧道内进行了同步的振动测试，测点主要分为隧道内测点和地面测点2个部分。隧道内测点布置在钢轨、轨道板及隧道壁面位置处，地面测点分别在距线路中心线0 m、7.5 m、15 m、30 m及50 m处布置。测试工点线路条件为普通减振、单线直线段，线路埋深20 m；地铁车辆为B型车，车速为60~70 km/h。测试点区域工程地质条件较为复杂，土层为残积砂质黏土，基岩有突起，存在花岗岩球状风化体，形成了上软下硬的复合地层特点。振动地面测试布点情况如图1所示。

图1 地面测点布置情况

3 振动测试结果及分析

3.1 隧道内振动测试结果

本次测试工况选取为普通道床，车型为B型车、车速为60~70 km/h，线路埋深约为20 m条件下的振动测试。钢轨振动以高频为主，主要振动频率范围为250~800 Hz之间；在0~200 Hz范围内，其振动幅值最大，各测试工点最大Z振级平均值为117.1 dB；对于普通道床，各测试工点最大Z振级平均值为92.8 dB；隧道壁处的最大Z振级平均值为83.8 dB。振动传播由钢轨→道床→隧道壁逐渐减少，符合振动传播衰减规律。

3.2 地面测试情况

地面测试点布置分别为距离隧道正上方0 m、7.5 m、15 m、30 m、50 m共5处测试点。测试工况的地面测试结果振动时程和振动频域曲线如图2所示。

图2 通过时段内列车0~50 m振动时程及频域曲线

通过测试结果可知，列车通过时地面振动测点主要振动频率范围为50~80 Hz之间；在0~15 m范围内，振级主要频率为63~80 Hz，根据多组测试数据的能量平均法计算得到0 m、7.5 m、15 m测点振级大小依次为78.6 dB、74.4 dB、66.0 dB；在30~50 m范围内，振级主要频率为50~63 Hz，30 m、50 m测点振级大小依次为61.0 dB、64.6 dB；地面测点Z振级最大处为0 m测点，Z振级最小处为30 m测点。

3.3 振动传播损失分析

综合隧道及地面振动测试结果，计算各处测点的VLZmax值，得到不同位置的最大Z振级结果如图3所示，计算振动经传递路径前后的差值而求得各个传播途径的传播损失值如表1所示。

图3 VLZmax随距离的变化规律

通过计算结果可以看出，钢轨振动幅值最大，振动由钢轨到道床的衰减也最大；振动由道床至隧道壁至地面衰减过程中，并非距离线路越远的测点振动水平越小，即：距离线路中线0~30 m之间，振动的衰减规律为由大逐渐减小；在50 m位置处，VLZmax大于30 m处的测试值，振动在30~50 m区域存在放大区。

研究表明[7]，振动放大区距隧道中心线的距离与地层条件、隧道埋深、振源机制及振动的频率有关。预测与本次研究区域测试条件相似的敏感点位置处的环境振动时，可以根据本研究给出的振动传播衰减规律回归公式进行预测计算。

4 振动传播衰减规律研究

城市轨道交通隧道段振动在土体中的传播受到地层、土质、地下水环境、边界反射条件、阻碍物，以及振动的频率、振动传播方向等多种因素的影响[8]。目前国内尚无成熟的振动模型可以借鉴，因而利用类比实测的振动衰减数据拟合曲线来建立预测模型。

根据《环境影响评价技术导则城市轨道交通》(HJ 453—2018)中提出的回归计算方法，给出适用于该地铁隧道振动传播衰减的经验公式，即

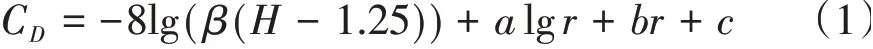
式中：CD为隧道壁振源处至地面测点振动传播衰减量，为隧道壁至隧道顶地面的衰减项，其中β为土层的调整系数；H为预测点地面至轨顶面的垂直距离，m；β值可通过隧道壁振源处至地面测点振动传播衰减量与隧道埋深H求得；algr+br+c为地面传播的衰减项，r为预测点至线路中心线的水平距离，m；a、b、c为需要确定的拟合参数，可根据测试数据的统计回归分析方法求得。

4.1 隧道壁至隧道顶部地面的衰减

隧道壁振源测点处至地面测点的振级大小与隧道埋深有关，即

根据实测结果，由隧道壁振源处至地面测点振动传播衰减量及埋深高度，计算得到的多组β值并求其平均值，结果如表2所示。

表2 隧道至地面衰减参数计算结果

由计算结果可得到由隧道壁振源处至地面测点振动传播衰减公式为

4.2 地面衰减及回归分析

结合弹性理论推导、半理论半试验和试验型经验公式，可统一表达为

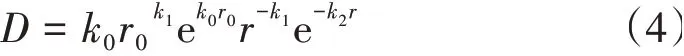
式中：D为距线路中心线r处相对于r0处的地面振动幅值之比；r0为地面参考点距离线路中心线的距离，m；k0为与振源有关的常数；k1为体波、面波合成的衰减特性系数；k2为土体对振动能量吸收衰减的特定系数。

公式（4）中的相关参数可通过采用幂函数和指数函数复合回归的方法得到，将公式（4）两侧取对数可得

对于测试数据，首先进行幂函数和指数函数的一元回归分析，根据得到的回归函数再进行二次拟合回归分析[6]。

本研究中利用编程软件编制了计算程序，通过输入监测数据，得到a、b和c的数值分别为-9.564、-0.108和1.105。对于该地铁线路的测试结果，将参考点定为0 m处测点，得到的地面振动传播衰减曲线与实测数据的回归分析如图4所示。

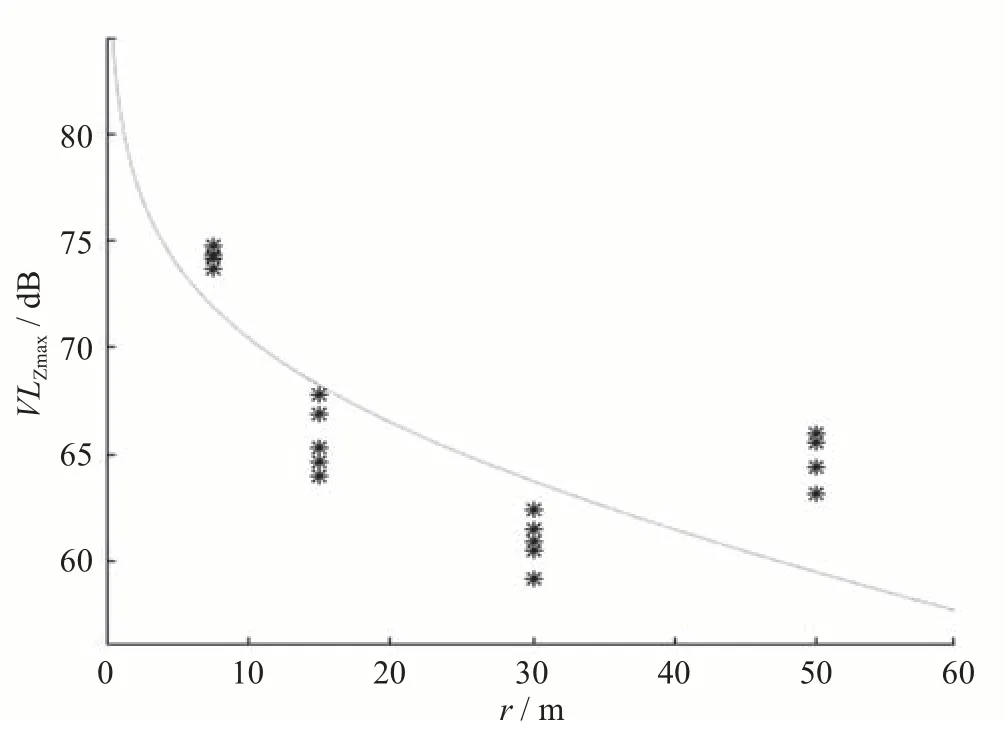
图4 回归分析曲线与实测结果拟合情况

由此可得振动的地面衰减公式为

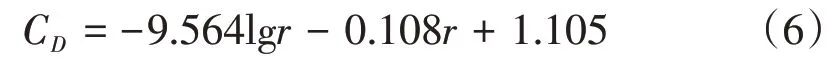
根据回归分析得到的拟合曲线可以看出，该拟合分析方法得到的结果在0~30 m内基本能够反映真实的振动衰减情况，30~50 m范围内由于存在振动放大区，拟合结果存在一定的偏差。

4.3 振动传播衰减预测回归公式

由隧道至地面、地面上传播衰减公式，可得城市轨道交通引起的地面振动传播衰减预测公式为

在计算任意距离的振动传播衰减数值时，可根据隧道埋深，通过带入与线路中心线的距离求得振动衰减值的大小。

5 结论

根据某城市地铁线路隧道及地面同步测试结果，得到了该城市轨道交通列车运行产生的钢轨、道床、隧道壁各点振动水平及传播过程中的传递损失，根据相关导则中的回归分析方法计算得到了振动传播衰减公式，形成结论如下。

（1）钢轨、道床、隧道壁振动水平由大变小，振动主频由高到低，其振动幅值大小符合传播衰减规律；车速在60~70 km/h时，钢轨、道床和隧道壁测点最大Z振级大小分别为117.1 dB、92.8 dB和83.8 dB，主要振动频率范围分别为250~800 Hz、20~100 Hz和40~80 Hz。

（2）通过测试结果可知，列车通过时地面振动测点主要振动频率范围为50~80 Hz之间；在0~15 m范围内，其振级主要频率为63~80 Hz，0 m、7.5 m、15 m测点振级大小依次为78.6 dB、74.4 dB、66.0 dB；在30~50 m范围内，振级主要频率为50~63 Hz，30 m、50 m测点振级大小依次为61.0 dB、64.6 dB。距离线路中心线0~30 m之间，振动的衰减规律为由大逐渐减小，50 m位置处的VLZmax大于30 m处的测试值，振动在30~50 m区域存在放大区域。

（3）地面振动在传播过程中存在振动放大区，其距隧道中心线的距离与地层条件、隧道埋深、振源机制及振动的频率有关。预测与本次研究区域测试条件相似的敏感点位置处的环境振动时，可根据本研究给出的振动传播衰减规律回归公式进行预测计算，其结果在0~50 m内基本能够反映真实的振动衰减情况，为了使预测结果更加准确，在进一步研究中需考虑振动放大区的影响。