一类非线性混料指数模型及其最优设计
陈嘉丽, 张崇岐
(广州大学 经济与统计学院, 广东 广州 510006)
0 引 言
混料试验设计[1-3]被广泛应用于食品加工、化工、医药、农业等行业,越来越受到大家的关注. 怎样保证估计量在精确性方面具有某种优良性质并且使试验成本较低,从而更有效地选取设计点,是混料试验设计的研究范畴. 目前的混料试验设计多是建立在线性模型上,如Fedorov[4]、Cornell[5]、Mandal等[6]和 Sinha等[7],这些模型可以用q变量系统的q阶多项式模型来表示[8-9]:
β12…qx1x2…xq,
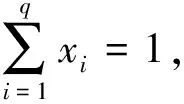
目前学者对线性混料模型研究甚多,研究手法较为成熟. 但实际应用中很多问题用线性模型去拟合总存在一定误差. 因此,对非线性混料模型[10-11]的最优设计问题进行研究十分必要.由于非线性混料模型信息矩阵的逆求解过于复杂,从而衍生出的一种方法是将原本的非线性模型进行泰勒展开,使其转化成常见的幂函数的线性模型. 此做法本质上解决的仍是线性问题,难免会产生一定的误差,因此,有必要对非线性混料模型进行更为深入的探讨. 2012年朱志彬等[12]基于becker模型提出了非线性分式混料模型, 并研究了二分量模型的 D-最优设计. 2015年张崇岐等[13]提出了一类含常数项的混料指数模型, 并直接在单纯形格子点上研究了模型的D-最优设计. 本文提出一类特殊的混料指数模型, 通过在试验域内多次迭代得到模型的D-最优设计,并用等价定理来证明该设计的D-最优性.
1 模型构造
实际生活中很多产品都是由多种物质混合制作而成的,如面包、药品和饮料等. 不同成分之间占比的变化将会影响最终产品的质量. 为了生产出质量更佳的产品,得到最优的配料比例,减少成本,需要寻找最优混料试验设计.
假设某产品有q种成分,它们在生产中的比例分别为x1,…,xq,显然x1≥0,…,xq≥0,且x1+…+xq=1.故混料的试验区域为
Sq-1={(x1,…,xq)|xi≥0,i=1,…,q,x1+…+xq=1}.
考虑一般的线性回归模型,其基本形式为
y=βTf(x)+ε,
其中,y是响应变量,ε是随机误差,β=(β1,β2,…,βk)T是k维未知参数向量,f(x)=(f1(x),f2(x),…,fk(x))T为已知的关于设计点x=(x1,x2,…,xq)∈Sq-1的实值函数向量.一般假设
E(ε)=0,Var(ε)=δ2.
与线性回归模型不同的是,非线性回归模型G(x,β)的一般表达式如下:
y=G(x,β)+ε.
目前国内对非线性混料模型的研究较少,常见的非线性混料模型包括非线性混料指数模型和非线性分式可加混料模型,其中以非线性混料指数模型更为常见.
现考虑二分量非线性混料指数模型
实践教学内容体系(表1)三个层次中,第一层次是基础层次:通过英语听说训练,学生能熟练地运用英语进行简单的英语交流;通过计算机实训,让学生掌握计算机的基本操作,能够运用计算机进行单据的制作和文件处理。在学生学习专业课之前,带领学生参观当地的外贸企业,也可以邀请企业人士到学校为学生作报告,使学生对外贸业务流程有一个大体的认识,激发学生的学习热情。
η=β1x1+β2eαx2+ε
(1)
其中,η是响应变量,β1,β2和α是待估参数,ε是均值为0、方差为σ2的随机误差,x1+x2=1.不失一般性,本文考虑当α=1时的情况:
η=β1x1+β2ex2+ε
(2)
就模型(2)讨论它的D-最优性,显然模型具有两个未知参数,因此,必须找到一个两点设计使其满足D-最优性. 设在试验区域X中的一个设计ξ为
其中,x1=(x11,x12),x2=(x21,x22)为不同的支撑点,0≤λ1,λ2≤1,λ1+λ2=1.记f(x)=(x1,ex2))T.
设计ξ所对应的信息矩阵M(ξ)为
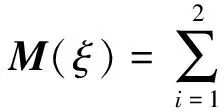
且与模型η相对应的方差函数为
d(x,ξ)=fT(x)M-1(ξ)f(x).
在混料试验设计中,若存在设计ξ*使得信息矩阵的M(ξ)的行列式最大化,即
|M(ξ*)|=max|M(ξ)|,
称ξ*为D-最优设计.
由等价定理可知,对连续回归模型与紧致空间而言,ξ*称为模型η的D-最优设计当且仅当ξ*满足
2 主要结果
根据D-最优准则可知,D-最优设计是最小化|M-1(ξ)|或最大化|M(ξ)|的设计.首先计算出模型(2)在设计ξ下的信息矩阵
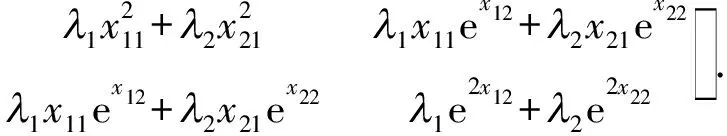
其次,计算设计ξ在模型(2)下的信息矩阵行列式
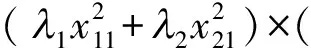
(λ1x11ex12+λ2x21ex22)2=
(λ1λ2)(x11ex22-x21ex12)2.
由约束条件λ1+λ2=1进一步可得
因此有
x21ex12)2.
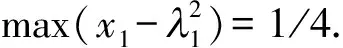
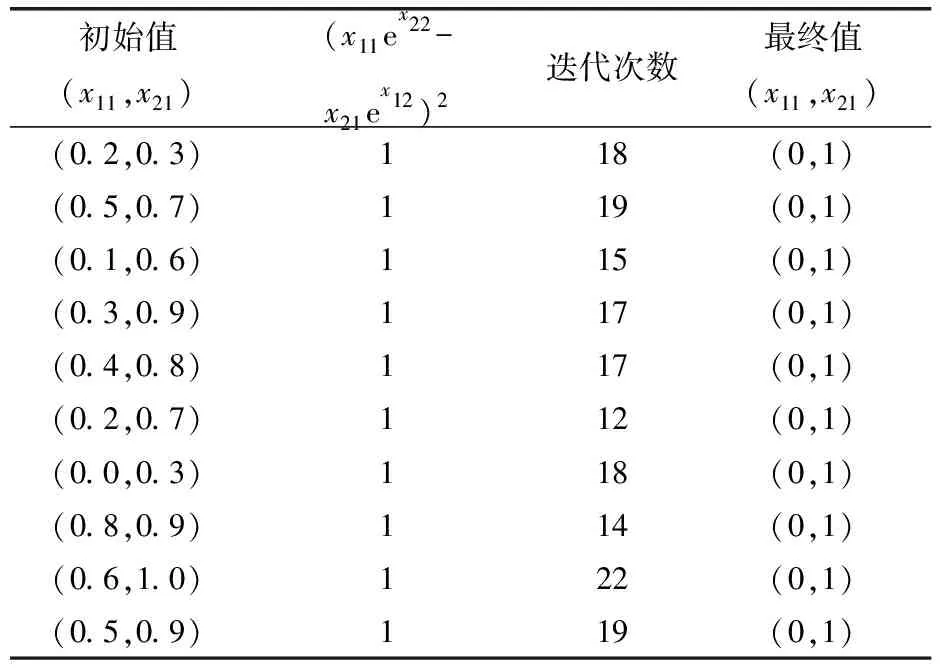
表1 f(x1,x2)函数的10组不同初始值计算结果
从表1可以知道,10组不同初始值对应的最终值都是(0,1),且(x11ex22-x21ex12)2=1,迭代次数在20次左右,显然另一设计点为(1,0).
此外,根据方程f(x1,x2)=(x1ex2-x2ex1)2,在区域0≤x1≤1,0≤x2≤1,用MATLAB画出对应的三维立体图形,从图1中也可以得到在(0,1)和(1,0)时,max((x1ex2-x2ex1)2)=1.
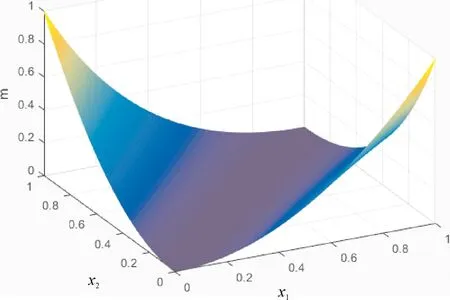
图1 f(x1,x2)函数的三维图Fig.1 The three-dimensional graph of the function f(x1,x2)
由此可以得到模型(2)的D-最优设计
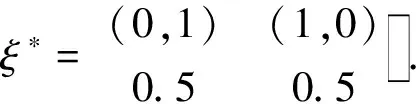
对于模型(2),证明所得的设计ξ*是设计域上的D-最优设计.该设计的信息矩阵M(ξ)与它的逆M-1(ξ)
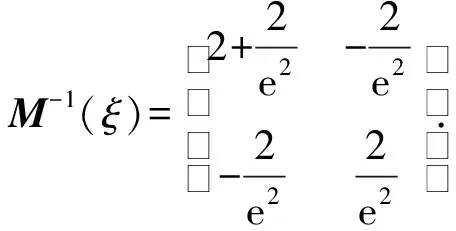
由此可得方差函数
d(x;ξ*)=fT(x)M-1(ξ)f(x)=
其中,0≤x1,x2≤1,x1+x2=1,通过MATLAB画出d(x;ξ*)在区间[0,1]范围的曲线图,如图2.
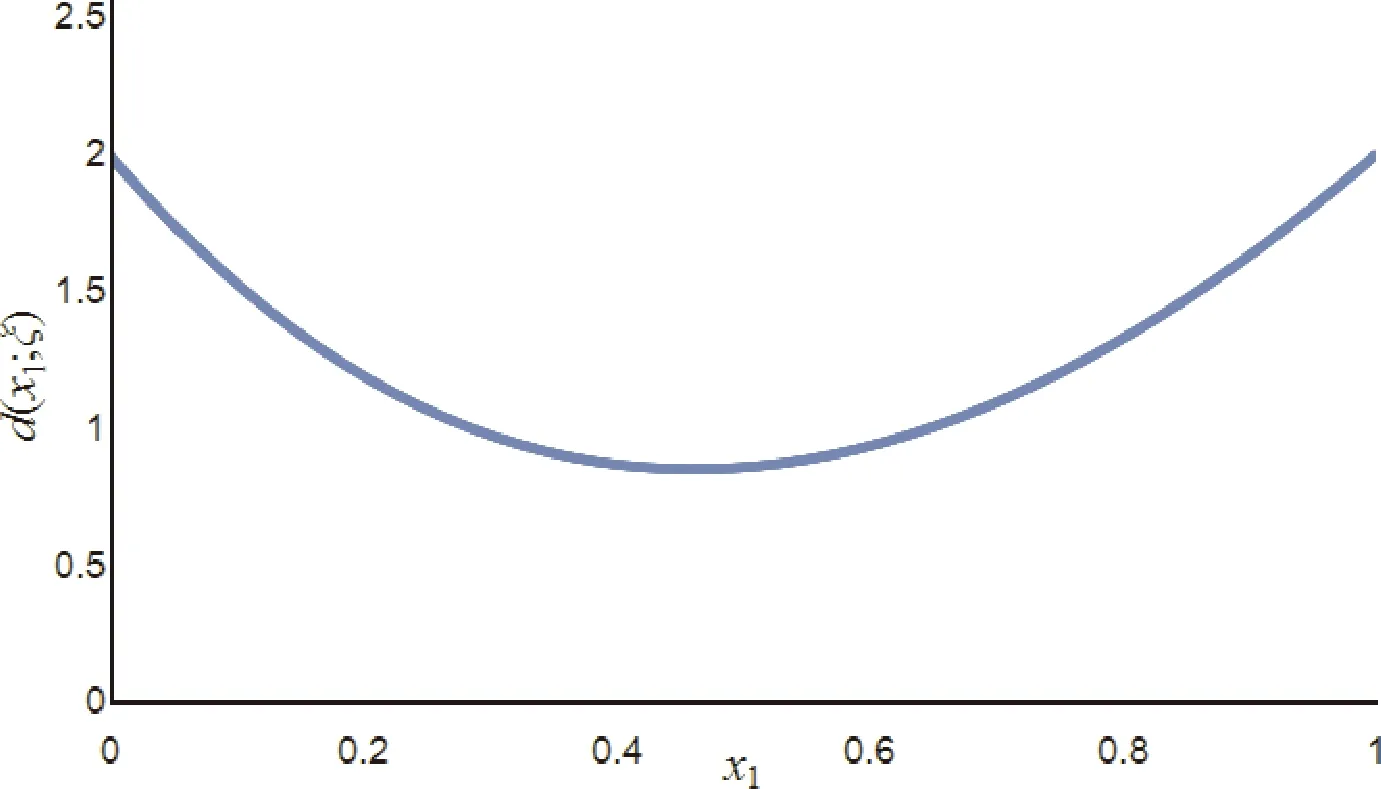
图2 d(x;ξ*)的曲线图Fig.2 The curve graph of d(x;ξ*)
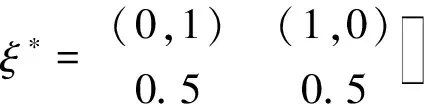
3 结束语
在各种不同的混料模型中,非线性混料模型因其在实际生活中存在广泛的应用价值而成为当前研究热点. 由于该模型计算非常复杂,算法效率低,没有一套相对完善的理论,因此,需要进一步的深入研究. 本文以二分量非线性混料指数模型为基础,通过多次迭代得到该模型的D-最优设计,并用等价定理来证明该设计的D-最优性. 在未来的研究中,可以考虑对更高阶的非线性混料指数模型的最优设计问题做出进一步探讨.

