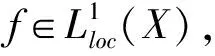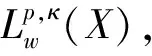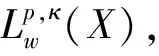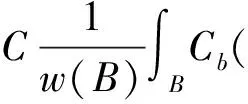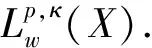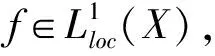The maximal commutators on weighted Morrey spaces
-
(School of Mathematics and Information Science, Guangzhou University, Guangzhou 510006, China)
Abstract: Let M be the maximal function and [b,M](f)(x)=b(x)Mf(x)-M(bf)(x) be the commutator of maximal functions. Let Cb be the maximal commutator. In this paper, we study the estimates for the commutator of maximal functions [b,M] and the maximal commutators Cb on weighted Morrey spaces on spaces of homogeneous type. The lower bound of the maximal commutator Cb is also obtained.
Key words: commutators; maximal function; weighted Morrey spaces
0 Introduction
In their remarkable result[1], Coifman—Rochberg—Weiss showed that the commutator of Riesz transforms is bounded onLp(Rn) if and only if the symbolbis in the BMO space. See also the subsequent result in Refs[2-7]. In Ref.[8], Bastero— Milman—Ruiz characterized the class of functions for which the commutator with the Hardy—Littlewood maximal function and the maximal sharp function are bounded onLp(Rn). Recently, in Ref.[9] Agcayazi, et al also studied the unweighted version of the maximal commutatorCb(f) onRnby using a different approach, and this was extended to a space of homogeneous type by Fu, et al in Ref.[10].
In this paper, we aim to provide a quantitative estimate for the commutator of maximal functions [b,M] and the maximal commutatorCbon weighted Morrey spaces on spaces of homogeneous type. To be more precise, let (X,d,μ) be a space of homogeneous type. The Hardy-Littlewood maximal functionMf(x) onXis defined as
where the supremum is taken over all ballsB⊂X. The commutator of maximal functions [b,M] is defined by [b,M](f)(x)=b(x)Mf(x)-M(bf)(x). The maximal commutatorCbonXwith the symbolb(x) is defined by
|f(y)|dμ(y),
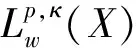
where
The main result of this paper is as follows.


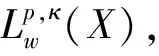
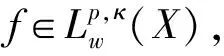
Throughout the paper, the letter “C” will denote (possibly different) constants that are independent of the essential variables.
1 Definitions and preliminary results
Letμbe a measure onXand letdbe a metric onX. Then we call topological spaceXto be a space of homogeneous type if it satisfies the doubling property, that is, there exists a constantC≥1, such that for all ballsB(x,r)={y∈X:d(y,x) μ(B(x,2r))≤Cμ(B(x,r))<∞. For the definition of homogeneous type space, one can see Ref.[11], Chapter 3. Using the doubling property, we can obtain that there existC,n>0 such that μ(B(x,λr))≤Cλnμ(B(x,r)) holds for allλ>1. The parameternis a measure of the dimension of the space. Letwbe a nonnegative locally integrable function onX. For 1 Here the suprema are taken over all ballsB⊂X. The quantity [w]Apis called theApconstant ofw. Next we note that forw∈Apthe measurew(x)dμ(x) is a doubling measure onX. In order to prove Theorem 1, we need the following lemma. ProofofTheorem1 This implies thatb∈BMO(X), and The proof of Theorem 1 is complete. In order to prove Theorem 2, we need the following lemma. |[b,M]f(x)|≤CCb(f)(x). ProofofTheorem2 Letp∈(1,∞),κ∈(0,1) andw∈Ap(X). From Lemma 2 and Theorem 1, we have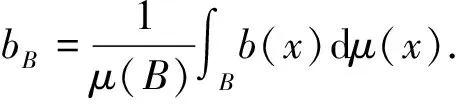
2 The proof of the main results