基于稳定性分析的开口钢箱梁吊装施工参数分析
张 鑫, 范 亮
(1.重庆汇中建筑施工图设计审查有限公司, 重庆 400700; 2.重庆交通大学, 重庆 400074)
钢-混凝土组合桥是由钢箱和混凝土桥面板组成,充分发挥钢材受拉以及混凝土受压的材料优势,具有自重小、无裂缝、快速装配等优势[1-3]。钢-混凝土组合桥中,由于钢箱梁主要用于受拉,成桥后钢箱顶面位于中性轴附近几乎不受力,因此,钢箱梁与钢箱中的构造形式有显著区别,一般为无顶板的开口钢箱梁,仅有较小的上翼缘用于安装剪力钉。钢-混凝土组合梁在施工过程中桥面板未安装就位时,开口钢箱梁刚度较小、稳定性较差,如2020年美国纽约州梅西桥在桥面板未安装前发生了严重的钢梁侧倾整体扭转失稳事故。
稳定性是桥梁的核心课题之一,国内外许多学者对桥梁成桥状态结构的稳定性做了大量研究[4-10],成桥状态结构所受荷载较为稳定,而在施工过程中,结构所承受的临时荷载值有可能大于运营状态下结构的设计荷载值,使得结构局部应力超过材料强度设计值或结构产生的变形过大而失稳,最终导致结构在施工过程中发生破坏[11-14],因此,施工过程中结构稳定性研究十分重要且必要。
本文运用有限元分析软件对钢箱梁吊装过程进行模拟,分析吊点间距、吊索与钢箱梁夹角等施工参数以及钢箱梁宽跨比、高跨比、腹板厚度、横隔板数量等结构参数对开口钢箱梁稳定性的影响,为开口钢箱梁设计及吊装施工控制提供参考。
1 结构屈曲稳定性分析理论
稳定性问题表现在加载过程中,构件在原有的平衡状态失去稳定性而转向新的稳定平衡,当荷载P=Pcr时,平衡分支即将出现,称Pcr为压屈荷载。
稳定(屈曲)分析可采用特征值屈曲分析预测理想弹性结构的理论屈曲强度(分叉点),通过提取使系统刚度矩阵([KD]+λ[KG])奇异的特征值来获得结构的临界失稳荷载及失稳模态。计算稳定安全系数的特征方程式为:
([KD]+λ[KG]){Δδ}=0
(1)
式中:[KD]为刚度矩阵;[KG]为初应力矩阵;λ为特征值。
若方程有n阶,则理论上存在n个特征值λ1,λ2,…,λn和对应的n个特征向量(失稳模态)。但只有最小的特征值或最小的稳定安全系数才有实际意义,此时特征值为λcr,临界荷载为:
Pcr=λcrP
(2)
开口钢箱梁吊装施工过程中,起吊的开口钢箱梁存在2种失稳的可能性:一是板件局部发生波浪形的凹凸变形,出现局部失稳;二是整体侧向失稳。本文将基于上述屈曲稳定性分析理论,采用特征评价稳定临界荷载与施工过程中开口钢箱梁的整体稳定性。
2 开口钢箱梁施工稳定性数值模型
2.1 工程背景
贵州省都匀至安顺公路第T9合同段K31+400车行天桥为钢混组合梁桥,天桥全长58 m,主梁采用“开口钢混组合梁+混凝土桥面板”的分幅组合结构,采用双主梁结构,截面中心处组合梁高2.5 m,其中钢箱梁高2.2 m,混凝土板厚0.25 m。
开口钢箱梁的宽度为3.4 m,腹板厚度为16 mm,底板厚度为38 mm,底板加劲肋厚度为22 mm,腹板加劲肋厚度为14 mm,钢材均采用Q420,其截面如图1所示。
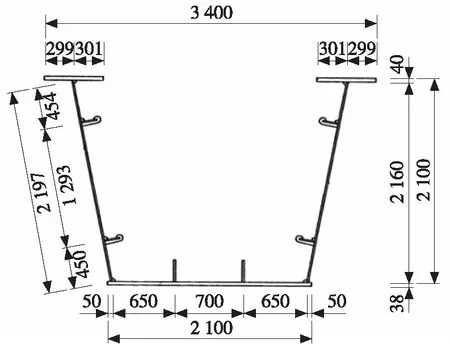
单位:mm
2.2 主要参数
考虑施工参数和结构参数对开口钢箱梁施工稳定性的影响。
施工参数主要包括吊点间距、吊索与钢箱梁平面的夹角。其中,吊点间距分别按照0.1L~1.0L(L为梁的吊装长度,间隔0.1L)逐级分析;夹角分别按照30°、40°、50°、60°、70°逐级分析。
结构参数包括宽跨比、高跨比、腹板厚度、横隔板数量。其中宽跨比按照0.15~0.19(间隔0.01)、高跨比按照0.09~0.13(间隔0.001)、腹板厚度按照12 mm~20 mm(间隔2 mm)、横隔板数量按照 0~7(间隔1个)个逐级分析。
2.3 有限元建立
采用Midas有限元分析软件,主梁、横隔板及加劲肋均采用板单元模拟,吊索采用桁架单元,吊索顶部固结,荷载包括开口钢箱梁的自重和作用在开口钢箱梁腹板的横向风荷载,风荷载大小为0.76 kN/m2。进行稳定性分析得到屈曲荷载系数,即稳定性系数。有限元模型如图2所示。

图2 有限元模型
3 吊装稳定性的施工参数分析
3.1 吊点间距对吊装稳定性的影响
不同的吊点间距起吊开口钢箱梁的稳定系数如图3所示。由图3可看出,随着吊点间距的增大,稳定系数呈增大趋势,即稳定性越稳定;吊索与钢箱梁平面夹角为30°时,稳定系数随着吊点间距增大而增大;吊索与钢箱梁平面夹角在40°~70°范围内,当吊点间距为0.1L~0.8L时,稳定系数随着吊点间距增大而增大,当吊点间距为0.8L~1.0L时,稳定系数随着吊点间距增大而减小。因此,吊点间距推荐值为0.8L。
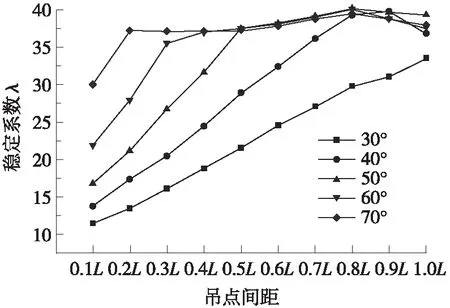
图3 稳定系数与吊点间距的关系曲线
在不同吊点间距下的开口钢箱梁发生局部和整体失稳临界点的夹角如图4所示。由图4可知,临界失稳点的夹角α′随着吊点间距增大而减小;吊点间距越小,整体稳定性越差,且更多为整体失稳;吊点间距越大,整体稳定性越好,且更多为局部失稳。
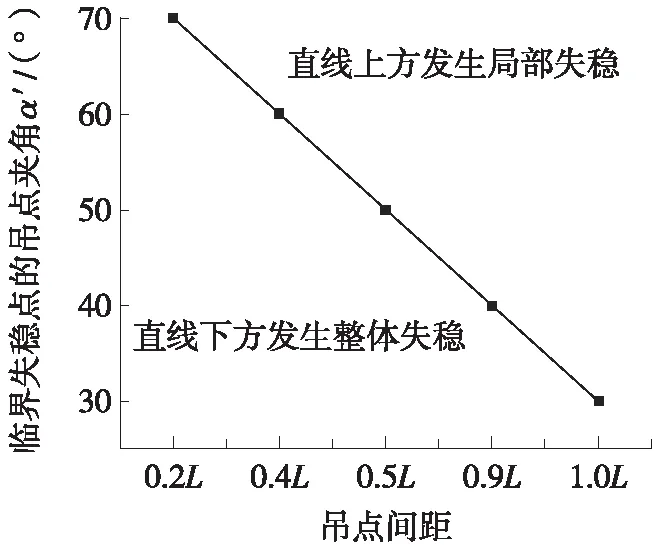
图4 临界失稳点与吊点间距的关系曲线
3.2 夹角对吊装稳定性的影响
吊索与钢箱梁平面的不同夹角下,开口钢箱梁的稳定系数如图5所示。由图5可知,当吊点间距为0.1L~0.4L时,夹角越大稳定系数越大,稳定性越好;当吊点间距为0.5L~1.0L时,夹角在30°~50°之间,稳定系数随着夹角增大而增大,夹角在 50°~70°之间,稳定系数随着夹角增大而有所减小。当夹角在50°左右时,开口钢箱梁的稳定系数最大,稳定性最好。

图5 稳定系数与夹角的关系曲线
在不同夹角下的开口钢箱梁发生局部和整体失稳临界点的吊点间距如图6所示。由图6可知,临界失稳点的吊点间距l′随着夹角α增大而减小;夹角越小,整体稳定性越差,更多是整体失稳;夹角越大,整体稳定性越好,更多是局部失稳。

图6 临界失稳点与夹角的关系曲线
4 吊装稳定性的结构参数分析
4.1 宽跨比
开口钢箱梁稳定系数与宽跨比的关系如图7所示。由图7可知,宽跨比为0.15~0.18时,稳定系数随宽跨比增加而增加;当宽跨比达到0.18以后,稳定系数逐渐减小。据此可知,开口钢箱梁宽跨比过大或过小都会降低其吊装时的稳定性,较优的宽跨比为0.18。

图7 稳定系数与宽跨比的关系曲线
4.2 高跨比
开口钢箱梁稳定系数与高跨比的关系如图8所示。由图8可知,高跨比为0.09~0.1时,稳定系数随高跨比增加而增加;高跨比为0.1~0.13时,稳定系数随高跨比增加而减小。由此可知,开口钢箱梁高跨比过大或过小都会降低其吊装时的稳定性,较优的高跨比为0.1。
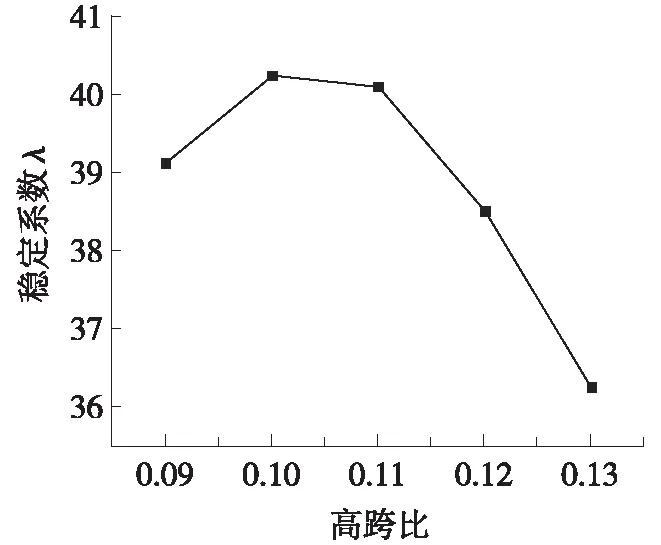
图8 稳定系数与高跨比的关系曲线
4.3 腹板厚度
开口钢箱梁稳定系数与腹板的关系如图9所示。由图9可知,开口钢箱梁稳定系数随腹板厚度增大而增大,腹板厚度越大,开口钢箱梁的稳定性越好。因此,在满足我国现行规范要求以及经济允许的条件下,可通过增大腹板厚度,提高结构的稳定性。
4.4 横隔板数量
开口钢箱梁稳定系数与腹板的关系曲线如图10所示。由图10可知,开口钢箱梁稳定系数随横隔板数量增加基本呈增加趋势,横隔板可保持截面形状、增强横向刚度,提高结构的稳定性,为此,在满足我国现行规范要求条件下,可适当增加横隔板数量,以提高结构的稳定性。

图9 稳定系数与腹板厚度的关系曲线
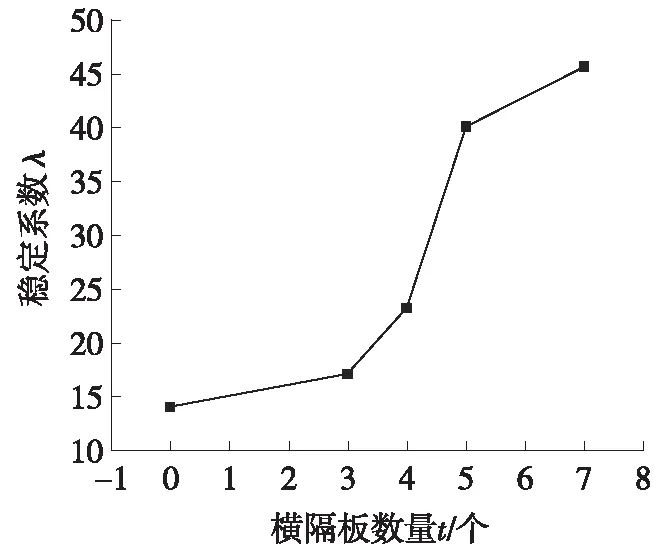
图10 稳定系数与横隔板数量的关系曲线
5 结论
本文考虑吊点间距、吊索与钢箱梁平面的夹角等施工参数及钢箱梁宽跨比、高跨比、腹板厚度、横隔板数量等结构参数,对吊装过程中开口钢箱梁的稳定性进行了分析,得到以下结论:
1) 开口钢箱梁稳定系数随吊点间距增大整体上呈增大趋势,吊点间距为0.8L时,开口钢箱梁的稳定系数出现最大值,稳定性最好。吊点间距越大,更易发生局部失稳;吊点间距越小,更易发生整体失稳。
2) 当吊点间距为0.8L、夹角在50°时,开口钢箱梁的稳定系数最大,稳定性最好。夹角越大,更易发生局部失稳;夹角越小,更易发生整体失稳。
3) 在吊点间距和水平夹角相同的情况下,开口钢箱梁的宽跨比、高跨比过大或过小,都会降低吊装过程中开口钢箱梁的稳定性;增加横隔板数量及增大腹板厚度都会提高开口钢箱梁的稳定性。
4) 为提高吊装过程中开口钢箱梁的稳定性,从设计上,可适当增加横隔板数量,增大腹板厚度,较合理的宽跨比为0.18,高跨比为0.1;在施工中,较优的吊点间距为0.8L,夹角为50°。

